Влияние структуры волны накачки на пространственные характеристики четырёхволнового преобразователя излучения на тепловой нелинейности в схеме с попутными волнами накачки

Методом функции размытия точки проанализировано качество обращения волнового фронта при вырожденном четырёхволновом взаимодействии на тепловой нелинейности в схеме с попутными волнами накачки с учётом их пространственной структуры. Показано, что в плоскости волн накачки ширина модуля функции размытия точки резко уменьшается с увеличением угла между плоскими волнами накачки. При фиксированном направлении распространения волн накачки учёт их расходимости приводит к дополнительному сужению модуля функции размытия точки.

При четырехволновом взаимодействии наряду с механизмом записи динамических решеток в нелинейной среде существенное влияние на качество преобразования изображения может оказать пространственная структура волн накачки. Так структура волн накачки в основном определят качество преобразования изображения при четырехволновом взаимодействии в средах с керровской нелинейностью [1-3]. Одним из наиболее распространенных механизмов записи динамических решеток, особенно в среднем диапазоне длин волн, является тепловой механизм [4-7]. Анализ качества преобразования излучения при четырехволновом взаимодействии на тепловой нелинейности проводился в приближении плоских волн накачки [8-9].

В настоящей работе с использованием метода функции размытия точки (ФРТ) анализируется влияние пространственной структуры волн накачки на качество преобразования излучения при четырехволновом взаимодействии на тепловой нелинейности в схеме с попутными волнами накачки

Пусть в плоском слое с тепловой нелинейностью толщиной t распространяются две волны накачки с комплексными амплитудами A ₁ и A ₂ и сигнальная волна с амплитудой A ₃ . В результате вырожденного четырехволнового взаимодействия генерируется преобразованная волна с амплитудой A ₄ (рис. 1).

Рис. 1. Схема четырехволнового взаимодействия с попутными волнами накачки

Четырехволновое взаимодействие будем рассматривать при следующих условиях:

• 1.    в приближение заданного поля по волнам накачки (| A ul » A 3,4 | ),

• 2.    при малом коэффициенте преобразования

• 3.    в приближении медленно меняющихся амплитуд

• 4.    при условии отвода тепла от граней нелинейного слоя.

(I A з| » A 4| ),

( dA,    d ² A,           )

k ^- » — - , j = 1 - 4 ,

I dz      dz ²                I

Тогда, как показано в работе [9], для плоских волн накачки

A 1,2 ⁽ r ) = A 1,2 ⁽ z )exP ( ^{- ik}\ 2 r )

с точностью до постоянного множителя амплитуда пространственного спектра сигнальной волны на передней грани нелинейного слоя A ₃( к ₃) связана с амплитудой пространственного спектра преобразованной волны на задней грани нелинейного слоя A ₄ ( к 4 , z = t ) выражением вида:

2 f_j

Л(к4, z = ^ = Е —--Г х j=1 Pj-K Tj

J 1     [ exp ( -P j ^) - exp ( ^K t /)]

[ ² sh ^к j       [к Tj + iPj ]

х [ exp ( к _Tj t - ip j t ) - 1 ] +

• 1     ^[ exp ( ^- P/) ^- exp ( ^-к t- ^ ) ]

• ²    sh ^к j       [к T - ip - ]

^{х [} exp ^(-к t- £ ^- ip - ^ ) ^- 1 ] + ^{[ eX}p ^^ ^{1 ]}

где f =

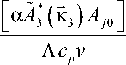
p - = ( k 3 - k - ) z , a -

кч =|к-0 -кз|, P- = 2a + ip-, коэффициент поглощения,

Л - коэффициент теплопроводности, c p - удельная теплоемкость, ^v - объемная плотность вещества A _{j 0} – амплитуда волны накачки на передней грани нелинейного слоя, к j 0 - поперечная составляющая волнового вектора k j , j = 1,2 .

Пусть сигнальная волна распространяется от точечного источника, расположенного на расстоянии z ₃ от передней грани нелинейного слоя (плоскость фокусировки сигнальной волны): A ₃( р , z 3 ) = 5 ( р -р 0 ). Будем рассматривать поле преобразованной волны на расстоянии z ₄ от задней грани нелинейного слоя (плоскость фокусировки преобразованной волны). Под четырехволновым преобразователем излучения будем понимать оптическую систему, состоящую из участка свободного пространства толщиной z ₃ , среды с тепловой нелинейностью, в которой распространяются две волны накачки, и участка свободного пространства толщиной z ₄ .

Функция размытия точки является Фурье-образом от амплитуды пространственного спектра преобразованной волны на выходе оптической системы при условии, что на ее входе оптический сигнал является точечным.

С учетом (1) выражение для функции размытия точки четырехволнового преобразователя излучения на тепловой нелинейности с попутными волнами накачки в центре поля зрения ( р ₀ = 0 ) с точностью до постоянного множителя имеет вид:

f_{j 0}

X

к

Tj

■» 2

G (р, z з , z 4 ) = f£ -

-” ^j = ¹ P j

[ 1    l"^exP ( ^-Р/ ) ^- exP ( ^к t /)"|

x) --------~------Г--------й------"X

^ 2 sh к Tj I           |к Tj + iP j I

X

+

1    [exp ( -P/ ) - exp ( -к t /)]

X

2 sh к _Tj I

i к 4 j р d к 4 j ,

( A x = | x 1 - x ₂1) и в плоскости, перпендикулярной плоскости волн накачки ( A у = | у 1 - у ₂1), где x ₁₂ и y _1,2 , определяются из условий:

| G ( x^ . y = 0)| = j G max , (3)

I G ( у 1,2 , x = 0 )| = 2 G max . (4)

Здесь G _max – максимальное значение модуля функции размытия точки.

Ширина модуля ФРТ характеризует разрешающую способность четырехволнового преобразователя излучения. При фиксированном положении плоскости фокусировки сигнальной волны существует оптимальное положение плоскости фокусировки преобразованной волны (плоскость оптимальной фокусировки), в которой ширина модуля ФРТ минимальна. Положения плоскостей оптимальной фокусировки преобразованной волны при рассмотрении ширины модуля ФРТ в направлениях, задаваемых осями ОX ( z 4 opt 0 ) ^{и 0Y} ( z 4 opt ± ) различны.

При фиксированном направлении распространения одной из плоских волн накачки, например, первой ( A ₁ ) изменение направления распространения второй волны накачки ( A ₂) приводит к изменению ширины модуля ФРТ в плоскостях оптимальной фокусировки, изменению положений плоскостей оптимальной фокусировки.

Будем рассматривать ширину модуля ФРТ в плоскостях оптимальной фокусировки, которые соответствуют плоским волнам накачки, падающим на нелинейную среду под одинаковыми углами I кi₀| = |к ₂₀|, к ₁₀ +к ₂₀ = 0 . Расчеты ширины модуля ФРТ будем проводить для излучения CO ₂ – лазера ( X = 10,6 мкм). В качестве нелинейной среды возьмем ацетон ( n = 1,36 , a = 0,004 мкм^-1) [7].

С увеличением угла между волнами накачки наблюдается резкое уменьшение ширины модуля ФРТ в плоскости волн накачки (кривые 1, 2 на рис. 2) и незначительное уменьшение ширины модуля ФРТ в плоскости перпендикулярной плоскости волн накачки (кривые 3, 4 на рис. 2).

Зависимость ширины модуля ФРТ в плоскости волн накачки от направления распространения волн при |к_{10 20}| [к « 1 хорошо описывается параболической функцией

A x = A x 0 {1 -Р[к10 -к20 ] 2} , (5) где A x0 - ширина модуля ФРТ при совпадении направления распространения волн накачки (к1 = к2), кj0 - проекция вектора кj на ось X, в - параметр, характеризующий скорость изменения ширины модуля ФРТ в зависимости от угла между волнами накачки, возрастающий с увеличением толщины нелинейного слоя.

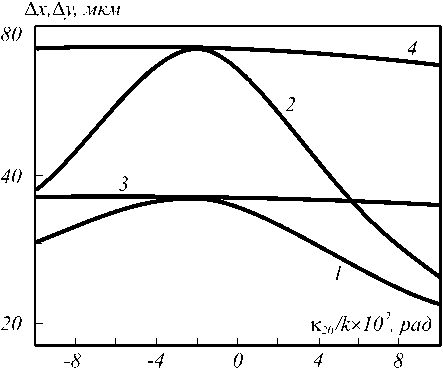
Рис. 2. Зависимость ширины модуля ФРТ в плоскости волн накачки (кривые 1, 2), в плоскости перпендикулярной волнам накачки (кривые 3, 4) от направления распространения второй волны накачки при к10 (к = 0,017рад, t = 400 мкм (2, 4), 200 мкм (1, 3)

С физической точки зрения, сужение модуля ФРТ в плоскости волн накачки с ростом угла между волнами накачки аналогично уменьшению ширины пятна при дифракции Фраунгофера на двух отверстиях с увеличением расстояния между отверстиями.

Пусть одна из волн накачки, например, вторая – является плоской, а пространственный спектр амплитуды первой волны накачки меняется по гауссову закону

A ( К 1 , z = 0) = exp

A 2 ^{( К} 2 , z = ⁰⁾ = 8 ( ^К 2 -

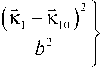
^К 20 ).

Здесь b – параметр, характеризующий расходимость волны накачки.

При учете пространственной структуры волн накачки ФРТ четырехволнового преобразователя излучения есть когерентная сумма функций размытия точки G(р, z3, z4, К1), соответствующих плоским волнам накачки

+х

G ( р , z 3 , z 4 ) = J G ( р , z 3 , z 4 , К 1 ) d К 1 .

-да

Численный анализ выражения (7) с учетом (2) и (6) показывает, что увеличение расходимости волны накачки приводит к монотонному уменьшению ширины модуля ФРТ, сближаются значения ширины модуля ФРТ в плоскости волн накачки и в плоскости перпендикулярной волнам накачки (кривые 1, 2 на рис. 3).

Для качественного анализа влияния расходимости волны накачки на вид ФРТ в плоскости волн накачки заменим ФРТ четырехволнового преобразователя с плоскими волнами накачки гауссовой функцией

G '( x ) = — exp a ₀

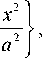
перетяжка которой связанна с шириной модуля ФРТ, определяемой (5), соотношением a = 0,6 Ax , а a 0 = 0,6 Ax0.

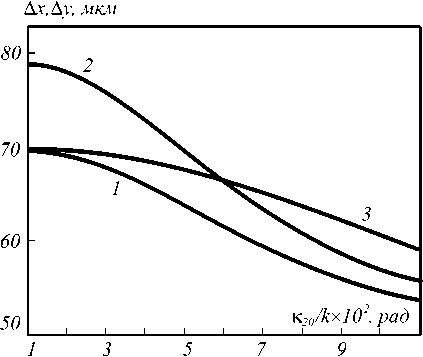
Рис. 3. Зависимость ширины модуля ФРТ в плоскости волн накачки (кривые 1, 3), в плоскости перпендикулярной волнам накачки (кривая 2) от расходимости второй волны накачки при к ₁₀/ к =0,017рад., t = 400мкм

Тогда с учетом расходимости первой волны накачки приближенное выражение для ФРТ примет вид:

G 2 ( x ) =

I     П Ь2

\j 2в b ² x ² + a ₀ ²

x

^^^^^^B

^{( к} 10   ^К 20 )

1 f. 2p b2 xx +1 1 + b I      a 0

На рис. 3 (кривая 3) приведена зависимость ширины модуля ФРТ от расходимости волны накачки, рассчитанная с использованием выражения (9). Наблюдается качественное согласие полученных зависимостей как с использованием точного, так и приближенного выражений для ФРТ. Однако с увели- чением расходимости волны накачки отличие между точным и приближенным значениями ширины мо- дуля ФРТ возрастает, что связано с нарушением па- раболической зависимости ширины модуля ФРТ в

случае плоских волн накачки с ростом угла между волнами накачки.

Воспользуемся приближенным выражением ФРТ (9) для определения «критического» значения расходимости волны накачки (bcr ), начиная с которой необ- ходимо учитывать влияние волны накачки на ширину модуля ФРТ. Пусть при «критическом» значении расходимости волны накачки ширина модуля ФРТ (Ax(bcr)) по сравнению с шириной модуля ФРТ для плоских волн накачки (Ax(0)) изменится на 10%:

^[ A x ( b cr ) -A x (0) ]

--0,1.

A x (0)

На рис. 4 приведена зависимость «критического» значения расходимости волны накачки от угла между волнами накачки. Видно, что с увеличением угла между волнами накачки «критическое» значение расходимости волны накачки возрастает. Толщина нелинейного слоя на характер зависимости b_cr от

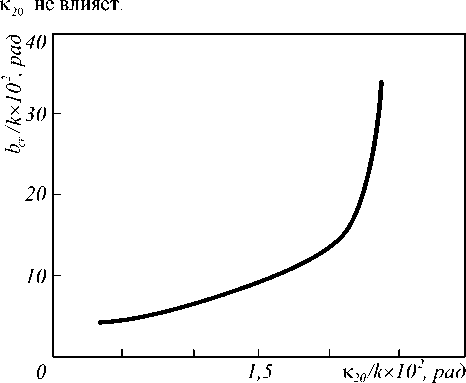
Рис. 4. Связь «критического» значения расходимости волны накачки и угла между волнами накачки при к ₁₀ /к =0,017рад, t = 400 мкм

Таким образом, влияние расходимости волны накачки на ширину модуля ФРТ четырехволнового преобразователя излучения на тепловой нелинейности в схеме с попутными волнами накачки будет наблюдаться лишь при «жесткой» фокусировке излучения в нелинейную среду, когда значение расходимости волны накачки превышает несколько градусов.

В заключение приведем оценки ширины ФРТ четырехволнового преобразователя излучения на тепловой нелинейности. При толщине нелинейного слоя t = 400 мкм и угле между волнами накачки два градуса при условии К ₁₀ + К ₂₀ = 0 для плоских волн накачки ширина модуля ФРТ в плоскости волн накачки A x = 69 мкм, в плоскости перпендикулярной волнам накачки A у = 77 мкм. Учет расходимости волны накачки b/ k = 0,16 рад приводит к сужению ширины модуля ФРТ в плоскости волн накачки до A x 1 =52,8 мкм, в плоскости перпендикулярной волнам накачки до A y ₁ =54,7 мкм.