Влияние сухого трения на устойчивость приборов с автоматическим уравновешиванием
Автор: Шамберов В.Н.
Журнал: Научное приборостроение @nauchnoe-priborostroenie
Рубрика: Оригинальные статьи
Статья в выпуске: 3 т.14, 2004 года.
Бесплатный доступ
Рассматривается аналитическая задача настройки прибора на устойчивый режим при наличии сухого трения в его подвижной части.
Короткий адрес: https://sciup.org/14264350
IDR: 14264350 | УДК: 620.178.162:
Текст научной статьи Влияние сухого трения на устойчивость приборов с автоматическим уравновешиванием
Сухое трение в подвижной части прибора не только определяет его нечувствительность к измеряемой величине, но также может вызывать автоколебательный режим, что часто является недопустимым при эксплуатации прибора. Влияние сухого трения на устойчивость прибора с уравновешиванием рассмотрим на примере прибора для измерения силы [1].
ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПРИБОРА
При построении математической модели прибора очень важно правильно учесть сухое трение в подвижной части прибора, что определяется целью исследования. Для рассматриваемого случая необходимо учитывать сухое трение при его некулоновской идеализации [2]. Структурно-функциональная схема типового прибора представлена на рис. 1.
Звено 1 преобразует разность сил f = f вх - f ос в перемещение x (см. рис. 1). Динамическая характеристика звена 1, преобразующего силу f в перемещение x , определяется способом крепления подвижной части. При закреплении подвижной части в подшипниках движение звена (с уче-
Рис. 1. Структурно-функциональная схема прибора том сухого трения) может быть представлено следующим описанием:
d2 x _ d x _ ы „
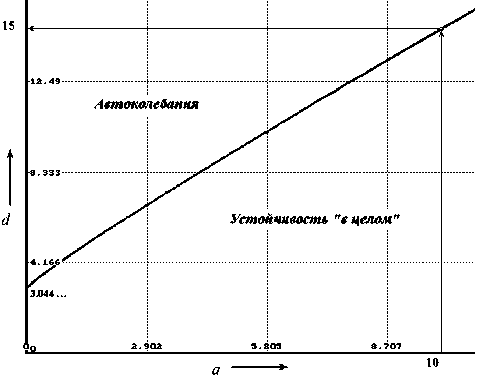
M-jT=0если 0 и f dt2d d2x dxd M —- + T — = f, если —^ 0 или(1) dt2 dtd если dx = 0 и И - FтP.0, dt где Md2 x /dt2 — даламберова сила (сила инерции); Tdx /dt — сила демпфирования; Ftp0 — сила трения покоя (сцепления), существующая до момента движения (страгивания) подвижной части прибора; M — масса подвижной части (н • с2 / м); T — коэффициент успокоения (н • с2 / м); x — перемещение подвижной части (м); f = fвх - fос — разность измеряемой и уравновешивающей сил ( н ). Звено 2 обычно включает в себя модулятор (преобразователь недокомпенсации с коэффициентом передачи Kпн), усилитель (с коэффициентом передачи Kус) и демодулятор (с коэффициентом передачи Kд). Пренебрегая инерционностью звена, можно считать, что u = Kx, где K = Kпн K ус Kд .(2) В приборе без корректирующих звеньев динамические свойства звена 3 определяются уравнением _ „ . , т d i„ d u = Ri + L--E —,(3) dtd где u — напряжение на входе звена (B); i — ток на выходе звена (A); R — активное сопротивление выходной цепи (Ом); L — индуктивность выходной цепи (Гн); E — электродвижущая сила, индуктируемая в обмотке обратного преобразова- теля при движении подвижной части (В). Звено 4, преобразующее ток i на выходе звена 3 (см. рис. 1) в уравновешивающую силу fос , является безынерционным и характеризуется коэффициентом передачи Kос . При проектировании приборов данного типа стремятся уменьшить параметр M (массу подвижной части прибора) по сравнению с параметром T (коэффициентом успокоения) и увеличить глубину уравновешивания Kос . Пренебрегая инерционными свойствами подвижной части прибора (M = 0) и используя в уравнениях (1)–(3) символ дифференцирования p = d / dt, динамику прибора можно охарактеризовать кусочно-линейной моделью [3] вида, представленного на рис. 2. Существенная нелинейность N ( f ) (см. рис. 2) определена учетом сухого трения в подвижном элементе прибора при пренебрежении его инерционными свойствами. Аналитическое описание нелинейности следующее N(f) = 0, если |f| < Fф.о и N(f) —= 0; N(f) = f, если N(f) - * 0 или (4) если N(f) — = 0 и |f| > Fтр.0. ВЛИЯНИЕ СУХОГО ТРЕНИЯ НА ВОЗНИКНОВЕНИЕ АВТОКОЛЕБАНИЙ Динамическая модель данного вида (см. рис. 2) была исследована методом точечных отображений на трехлистной фазовой плоскости [4]. Применительно к рассматриваемой задаче результаты исследования следующие. Динамическая модель устойчива "в целом" (при любых начальных условиях все движения притягиваются состояниями равновесия), если а) при (TR + KосE)2> 4TLKосK выполняется условие f А D — X \ A + 1 - D > (D - 1)exp|--ln----- ( A -1 D - A J б) при (TR + Kос E)2 < 4TLKосK выполняется условие 2 - D > > 7(1 - D)2+ Ai2 ехр A1 | arctg I 1 - D A1 +211 /J в) при (TR + KосE)2= 4TLKосK) — условие D < 1.782..., (7) где N(f) _ — предыстория состояния элемента с трением. где D = 1.782... определяется из выражения 2 - D = (D - 1)exp| D -1 В выражениях (5)–(7) обобщенные параметры A, A1, D определяются как A1 = - в / a, A = a1 / a, D = KосE / aLT. При этом в и а (при определении параметра A1 ) — соответственно мнимая и вещественная части комплексно-сопряженных корней Я1 2 = а ± je уравнения TL^ + + (TR + KосE)Л + KосK = 0; и а = Х1, а1 = Х2 (при определении параметра A) — вещественные корни (причем а > а1) этого же уравнения. При невыполнении любого из условий (5)–(7) сухое трение вызовет в модели автоколебания. В пространстве других параметров (a,d ) условия представлены на рис. 3, где a = KосE / TR ; d = = Kос (KL - ER)/TR2. Допустим, что исходные коэффициенты (за исключением коэффициента K ) определены так, что a = 10, d = 0.25K -10 = 15, тогда значение коэффициента K должно быть выбрано K < 100 (см. рис. 3). Условия (5)–(7) для принятой модели являются необходимыми и достаточными. При учете в законе сухого трения, помимо силы трения покоя (сцепления) также и силы трения движения (скольжения), условия являются достаточными. Рис. 3. Структура разбиения пространства параметров модели на области качественно различного динамического поведения Условия (5)–(7) сохраняются для любых значений Fтр.0 . ЗАКЛЮЧЕНИЕ Достаточно распространенное моделирование сухого трения в виде кулоновской идеализации (не учитывающей превышение сил трения покоя над силами трения движения) не позволяет выявить причину возникновения автоколебательных режимов. Решение задачи по влиянию сухого трения на возникновение автоколебательных режимов с помощью некулоновской идеализации можно осуществить аналитически, если допустимо пренебречь инерционными свойствами подвижного элемента прибора. Этот прием и продемонстрирован в статье.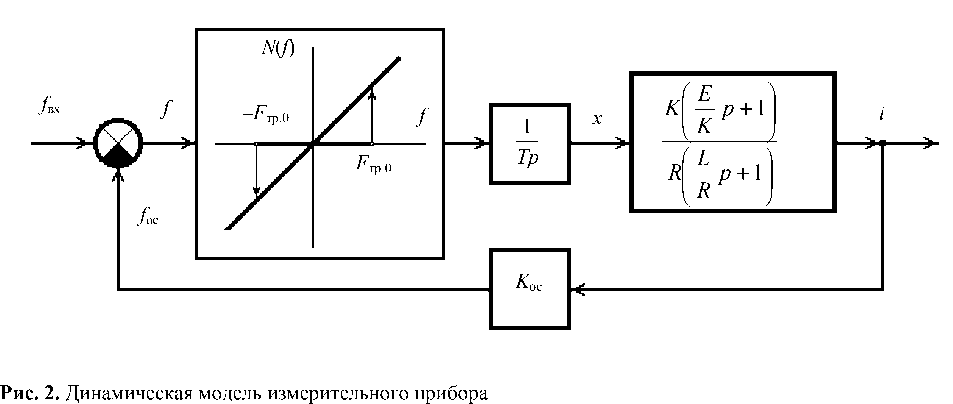
Список литературы Влияние сухого трения на устойчивость приборов с автоматическим уравновешиванием
- Туричин А.М. Электрические измерения неэлектрических величин (4-е издание)/Под общей ред. П.В. Новицкого. М.-Л.: Энергия, 1966. 690 с.
- Шамберов В.Н. Моделирование динамики элемента с трением//Фундаментальные и прикладные проблемы теории точности процессов, машин, приборов и систем: Труды 6-й сессии Международной научной школы (Фридлендеровские чтения). СПб.: Институт проблем машиноведения РАН, 2003. С. 98-105.
- Шамберов В.Н. Метод аналитического исследования влияния сухого трения на поведение авторегулируемых динамических систем//Научное приборостроение. 2003. Т. 13, № 3. С. 77-83.
- Шамберов В.Н. Исследование типовой промышленной системы автоматического регулирования с некулоновой моделью сухого трения. Автореф. дис. … канд. техн. наук. Л.: ЛГУ, 1988. 16 с.


