Влияние сухого трения в исполнительных механизмах автоматических систем с приводным электродвигателем на их устойчивость

Впервые электрическая машина для автоматического регулирования была применена в 1871 г. русским ученым-инженером В.Н. Чеколаевым. Новшество быстро нашло распространение в военной технике благодаря стараниям выдающегося русского артиллериста В.Ф. Петрушевского и талантливого изобретателя в области минного дела и артиллерии А.П. Давыдова. В настоящее время электрические машины широко используются в современных системах автоматического управления, автоматических устройствах и приборах.

В автоматических системах электрические машины часто используются в качестве исполнительных электродвигателей, преобразующих подводимый к ним электрический сигнал в угловую скорость вращения вала. С валом связан управляющий рабочий механизм, образующий с электродвигателем исполнительный механизм автоматической системы.

Присутствие сухого трения в исполнительном механизме может вызвать автоколебательный режим и привести к аварийной ситуации. Исследование явления требует создать в рамках сформулированной задачи идеализацию этого явления в виде определенной математической модели, допускающей возможность применения известных методов исследования.

МОДЕЛИРОВАНИЕ ДИНАМИКИ ИСПОЛНИТЕЛЬНОГО МЕХАНИЗМА ПРИ УЧЕТЕ СУХОГО ТРЕНИЯ

Уравнение динамики исполнительного механизма с приводным электродвигателем получим из уравнения равновесия моментов (1) и уравнения электрического равновесия (2):

( c м i = J дв

I

+J jр J

dQ

-+ M

d t

вн.тр.

( Q ),

где приведенный к валу двигателя динамический момент обусловлен инерционностью ротора ( J _дв ) и инерционностью связанного через редуктор ( j _р — передаточное число редуктора) с валом двигателя рабочего механизма ( J _м); c _м i = М — вращающий момент двигателя; c _м — коэффициент пропорциональности; М _{вн тр} ( Q ) — приведенный к валу двигателя момент от сил внешнего трения; Q — угловая скорость вращения вала;

L d i + Ri + c Q = U , d t ^е

где i — ток якоря; L — суммарная индуктивность; R — суммарное активное сопротивление; c _е Q — противо-ЭДС двигателя; c _е — скоростной коэффициент двигателя.

Момент от сил внешнего трения М _{вн тр} ( Q ) представляет собой сумму двух моментов: от сил вязкого трения М _втр ( Q ) = к _т Q ( к _т — положи -тельный коэффициент, характеризующий вязкое трение) и от сил сухого трения М _{с тр} ( Q )

М вн.тр. = М b.tp. ( Q ) + М c.tp. ( Q ).

Для М _{с тр} ( Q ) выполняется:

|^М с лр,| <  ^М тр.0 ,                ^{если Q} = 0;

М ср. = М ( Q ) с_Лр^в. Sign( Q ), если Q ^ 0,

где М _тр.0 — момент сил трения покоя, а М ( Q ) _стрдв — момент сил сухого трения движения.

Так что для момента сил внешнего трения справедливо

|М вн.тр.| <  М тр.0 , ^{если Q} = °;

М вн.тр. = к т Q + М ( Q )_СЛ1МП, Sign( Q ),        ⁽³⁾

если Q ^ 0.

Момент сил сухого трения движения — монотонно убывающая положительная функция, характеризуемая:

своим максимальным значением

М(Q)с.тр.дв. ^ Мтр.ост. при QH 0 , минимальным значением

М (Q) с.тр.дв. ^ Мтр.тт при |^Н “ , максимально отрицательным наклоном kТ = -(4(М (Q)     1 dQ|    .

При этом М тр.о >  М тр.ост. >  М тр.т. >  0 [1, 2].

Долгое время практика моделирования сухого трения в исполнительных механизмах ориентировалась на его простейшую идеализацию ^М тр.о = ^М тр.ост. = ^М тр.тт >  ⁰ , ^полУ^чившУю ^название кулоновской. Качественной особенностью некулоновских идеализаций является учет превышения сил трения покоя над силами трения движения: ^М тр.0 >  ^М тр.ост. = ^М тр.тт >  ⁰ — Учет сУХого трения по Булгакову; М тр.0 = М тр.ост >  ^М тр _mn >  ⁰ — учет сухого трения по Хайкину; М _{тр 0} >  М тр _ост > >  М _{тр min} >  0 — уточненный учет сухого трения.

По уравнениям (1–3) получим следующую модель исполнительного механизма:

L d i = - Ri - c _e Q + U ;

d t            ^е

J ^ = 0, если Q = 0 и| c _M i |< M 0;

d t

J d Q = - к т Q - M ( Q ) _с .т _РДВ , Sign( Q ) + c м i ,

если Q ^ 0;

J dz" = - k т ^Q - M ^{( Q )} с.тр.Дв. Sign c м i ) ⁺ c м i ’ если Q = 0 и| c м i |> M тр.0 ,

Здесь J — приведенный к валу двигателя момент всех вращающихся масс. Коэффициенты с _м , с _е могут быть определены по механическим характеристикам двигателя. При М _{тр 0} >  М тр _ост модель (4) относится к моделям логико-динамического класса. Переменными состояния являются угловая скорость вращения вала Q = d 0 / d t , угол поворота 0 и ток в обмотке якоря i , внешним воздействием — подводимое к якорю двигателя напряжение U .

Использование модели (4) сопряжено с существенными трудностями при аналитическом исследовании. Однако практика моделирования динамики автоматических систем с исполнительными двигателями малой мощности часто допускает пренебрежение моментом инерции ( J = 0), что позволяет применить вырожденную модель [3] исполнительного механизма в классе кусочнолинейных моделей (представлена на рис. 1 в операторном виде: p = d / d t — символ дифференцирования по времени). Коэффициент k в модели характеризует трение движения. Сухое трение учтено с помощью существенной нелинейности N ( M ) . Нелинейность соответствует учету сухого тр^ения при ^М тр.0 >  ^М тр.ост. >  ^М тр.mi _n >  ⁰ и k т >  k т .

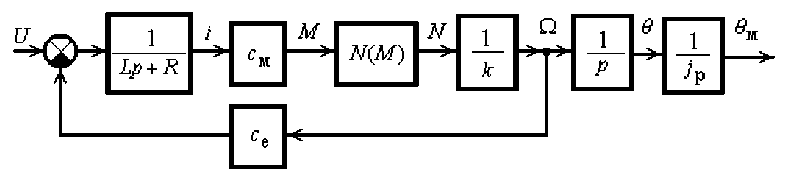
Рис. 1. Математическая модель исполнительного механизма с электроприводом

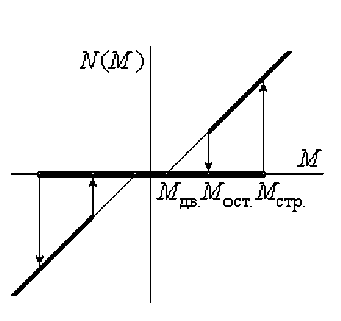
Рис. 2. Существенная нелинейность, определяющая учет сухого трения в исполнительном механизме при J = 0 и к _т >  к _т

Здесь обозначены: M _стр — страгивающий момент двигателя; M _ост — остановочный момент; M _дв — момент сил сухого трения при движении; N ₀— предыстория состояния нелинейности N ( M ).

Геометрическая интерпретация нелинейности представлена на рис. 2.

Значения M стр. = c м i стр. , M ост. = c м i ост. могут определяться экспериментально путем замера токов якоря, при одном из которых подвижная часть механизма приходит в движение ( i _стр ) и при другом — останавливается ( i _ост ) соответственно. Фрикционные колебания в модели (представлены на рис. 3) будут наблюдаться при выполнении условия

c _е c _м kR

+1 >

^M стр.

M ост.

Аналитическое описание нелинейности:

если M\ <  M _ост . ,                   то N = 0;

если |M| < Mстр. и |М| > Mост. и Nо = 0, то N = 0;

если M > Mn„T и Nn * 0 или ост.0

если M > Mстр. и N0 = 0, то N = M - Мли;

дв. ’ если M < -Мп„ и Nn * 0 или ост.0

если M < -M и N = 0, стр.0

то N = M + М„„ .

дв.

для внешнего воздействия U из диапазона

R ^M стр. <  U <  ^M ост. R c е c м c м           c м ( ^Rk

+ 1

)

Фрикционные колебания — быстрые скачкообразные перемещения, чередующиеся с остановками подвижной части исполнительного механизма, наблюдаются в модели механизма только при к _т >  к _т.

Рис. 3. Фрикционные колебания исполнительного механизма. Параметры системы: c _е = 0.2 В^с/рад, c _м = 1.0 Н^м/А, к = 0.1 Н^с/рад, R = 3.0 Ом, L = 0.032 Гн, M с_тр. = 4.00 Н^м, M о_ст. = 3.65 Н^м, M _дв. = 0.00 Н^м

U

у

Модель исп. механизма по рис. 1

^м

Рис. 4. Математическая модель следящей системы с электроприводом

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ АВТОМАТИЧЕСКИХ СИСТЕМ С СУХИМ ТРЕНИЕМ В ИСПОЛНИТЕЛЬНОМ МЕХАНИЗМЕ

Рассмотрим некоторые примеры влияния сухого трения в исполнительных механизмах электрических следящих автоматических систем на возникновение в них автоколебаний. Простейшая следящая система с приводным электродвигателем и безынерционным усилителем с коэффициентом передачи К _у [4] представлена на рис. 4.

Аналитическое описание нелинейности, учитывающей сухое трение:

Если \M\ <  M _дв . ,                   то N = 0;

если |M| < Mстр. и |М| > Mдв. и Nо = 0, то N = 0;

если M >  М„ и Na ^ 0 или дв.         0

если M >  M _стр . и N ₀ = 0,

то N = M - М„„;

дв.

если M < - М„. и Na ^ 0 или дв.         0

если M < -Mстр. и N0 = 0, то N = M + Млв.

дв.

Геометрическая интерпретация нелинейности представлена на рис. 5.

Нелинейность учитывает сухое трение при ^М тр.0 >  ^М тр.ост. >  ^М тр mn >  ⁰ , k т <  k т и имеет качественные отличия от нелинейности (см. рис. 3), учитывающей сухое трение при к _т >  к _т. При такой нелинейности (см. рис. 5) исполнительный механизм не генерирует фрикционные колебания, однако в самой автоматической системе сухое трение может вызвать автоколебания.

В режиме свободных движений динамика автоматической системы будет соответствовать модели

U + g 1 U = - d 1 N (U ) - d 2 N (U ).         (6)

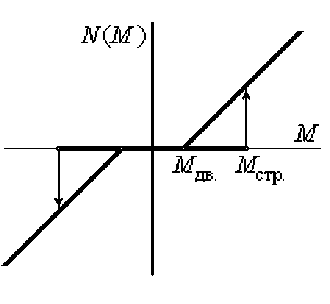
Рис. 5. Существенная нелинейность, определяющая учет сухого трения в исполнительном механизме при

J = 0 и к _т <  к _т

Динамическая модель (6) была исследована методом точечных отображений [5, 6]. Результаты исследования: модель устойчива "в целом", если выполняются условия:

а) при ( g 1 + d 1 ) 2 >  4 d 2

( A + 1 - D ) Q >  ( D - 1) exp f- - A - In D -l ) ;   (7)

I A - 1 D - A J

б) при ( g 1 + d 1 ) 2 <  4 d 2

(2 - D ) Q >

V(1 - D )² + A ² ехр

A 1

(     1 - D arctg——

A

в) при ( g 1 + d 1 ) 2 = 4 d ₂

+ n ]

J

(2 - D ) Q >  ( D - 1)exP

^{D - 1} J

В выражениях (7–9) обобщенные параметры A > 1; A1 > 0; D, Q > 1 определяются как A1 = - в / a, A = a1/ a, D = - d 1 / a. При этом в и а (при определении параметра A1) — соответст- венно мнимая и вещественная части комплексносопряженных корней Х12 = а ± je уравнения Я2 + (g 1 + d 1)Я + d2 = 0, а а = Я1 и а1 = Х2 (при определении A ) — вещественные корни (причем а > а1) этого же уравнения. Качественный учет сухого трения характеризует обобщенный параметр Q = (Mс1р. + Mдв.)/(MсТр. - Mдв.): с увеличением Q область устойчивости расширяется. Структура разбиения пространства в соответствии с условиями (7–9) на области устойчивости и области автоколебаний представлена на рис. 6 (значение параметра Q зафиксировано).

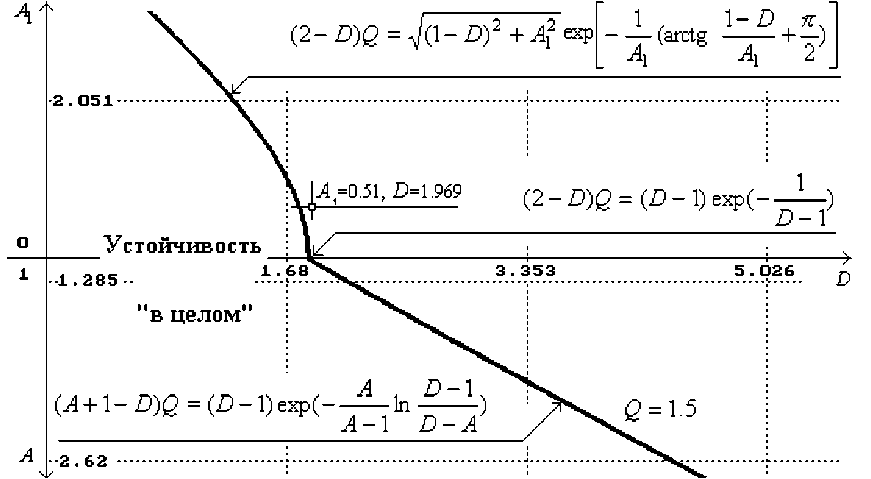
Рис. 6. Структура разбиения пространства обобщенных параметров A , A 1 , D, Q на области устойчивости и автоколебаний

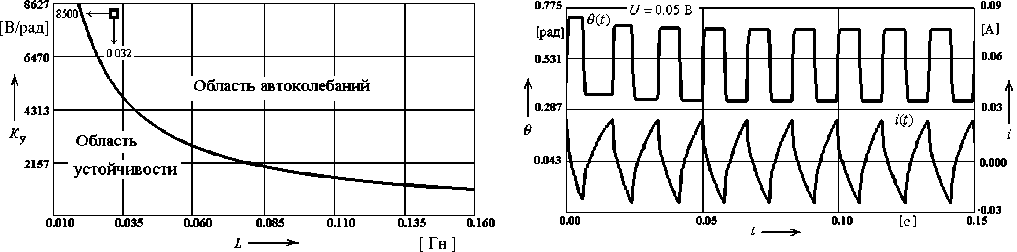
Рис. 8. Автоколебания в следящей автоматической системе с параметрами:

c _e = 0.2 В^с/рад, с _м = 1.0 Н^м/А, к = 0.01 Н-м-с/рад, R = 3.2 Ом, L = 0.032 Гн, М с_тр. = 1.00 Н^м, М о_ст. = = 0.25 Н^м, K у = 8500 В/рад

Рис. 7. Структура разбиения пространства исходных параметров (коэффициентов) на области устойчивости и автоколебаний при константных значениях:

R = 3.0 Ом, к = 0.01 Н-м-с/рад, c _e = 0.2 В^с/рад, с _м = = 1.0 Н-м/А, М с_тр. = 1.00 Н^м, М о_ст. = 0.25 Н^м

Невыполнение любого из условий (7-9) вызовет в модели автоколебания. Параметры обобщенной модели (6) определяются через исходные коэффициенты системы согласно выражениям: d 1 = c е c м / ^L k ; d 2 = K у c м / ^Lkj р ; g 1 = R / ^L . Структуру разбиения можно представить и в исходных параметрах (коэффициентах), например на плоскости K _у и L при фиксированных остальных параметрах (представлено на рис. 7).

Зададим параметрам Ky, L значения из облас ти существования автоколебаний K у = 8500, L = 0.032 (см. рис. 7), или А1 = 0.51, D = 1.969 (см. рис. 6). При начальных условиях, соответствующих области притяжения предельного цикла, в системе возникают автоколебания (представлены на рис. 8).

Рассмотрим пример [4] следящей системы, в которой используется пассивное дифференцирующее звено (рис. 9) с параметрами T 1 и T , при T >  T 2 .

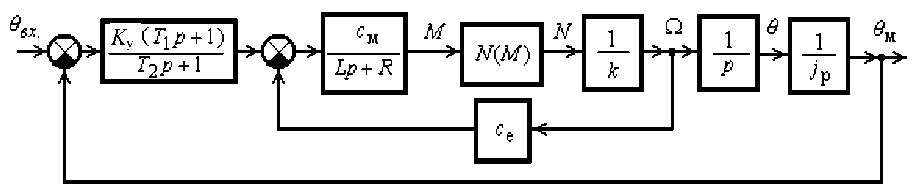
Рис. 9. Математическая модель следящей системы с пассивным дифференцирующим звеном

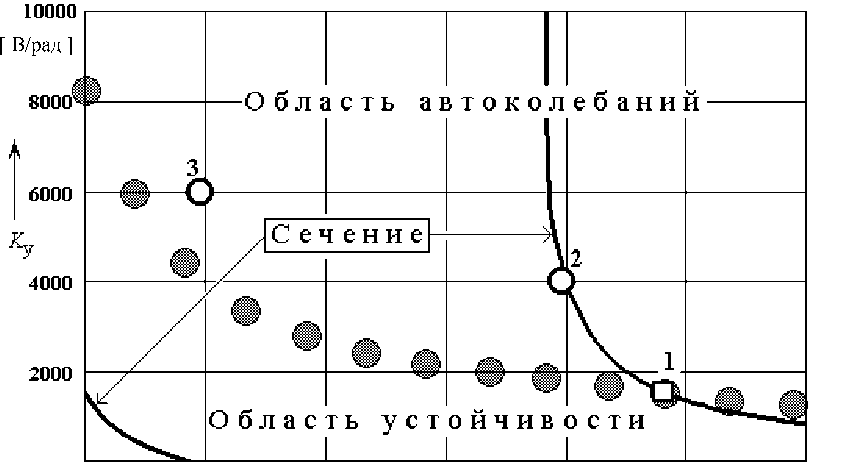
Рис. 10. Структура разбиения пространства исходных параметров следящей системы с дифференцирующим звеном на области устойчивости и автоколебаний

[ Гн ]

Следящая система с дифференцирующим звеном в отличие от системы рис. 4 является моделью 3-го порядка, однако и к ней (при L ^ RT 2 ) можно применить условия (7–9), определяющие ее устойчивость для определенного соотношения (сечения) ее параметров.

В соответствии с методом сечений пространства параметров [7, 8], для системы рис. 9 можно получить одно сечение, которое определяется уравнением

K y

Rc e i p ( L - RT 2 ) L ( L - RT 1 )

.

На плоскости параметров Kу , L сечение вы- глядит в виде двух линий (рис. 10). При выполнении равенства (10) условия устойчивости автоматической следящей системы 3-го порядка совпадают с условиями устойчивости системы 2-го порядка, для которой g 1 = 1/ T2, d 1 = cе cм / Lk, d2 = Kуcм / RkjрT2. Применение метода показало, что для точек сечения при L < RT2 система (6) всегда устойчива, для точек сечения при L > RT1 условия устойчивости (отсутствия автоколебаний) — L > 0.1267.., Kу < 1552 (квадратная точка 1, см. рис. 10).

Остальные точки граничной линии (овальные заштрихованные на рис. 10) получены методом машинного моделирования. Граничная линия раз- деляет плоскость параметров Kу , L на область устойчивости и область автоколебаний (графики автоколебаний для точек 2 и 3 сходны с графиком рис. 8).

ЗАКЛЮЧЕНИЕ

Исследование влияния сухого трения в исполнительном механизме приборной следящей системы осуществлено в результате сочетания методов: теории релаксационных (разрывных) колебаний, сечений пространства параметров, точечных отображений и численного интегрирования уравнений динамической модели, что вполне соответствует новой технологии научного познания — совместному использованию строгого анализа и численной машинной математики.