Влияние тепловых нагрузок на механические части турбоагрегата

Суммарное процентное соотношение по производству электроэнергии на атомных электростанциях от общего количества производимой энергии составляет 16%. Принцип работы АЭС заключается в преобразовании тепловой энергии пара в механическую энергию вращения вала паровой турбины, которая приводит в действие генератор, где механическая энергия преобразовывается в электрическую. Для предотвращения неполадок работы станций необходим контроль и усовершенствование работы оборудования АЭС. Поэтому актуален вопрос исследования переходных режимов работы паровых турбин.

Переходными считаются режимы, связанные с изменением расхода водяного пара или его параметров во времени [1].

К переходным режимам работы турбоагрегатов относятся такие процессы как пуски и остановы турбины. Эти режимы связаны со значительными изменениями механического и термического состояния элементов турбины и паропроводов.

В нашей работе проводится оценка величины напряжения сжатия. При возрастании температуры среды за очень короткий промежуток времени динамические эффекты становятся весьма значительными, напряжения сжатия достигают больших значений, часто в несколько раз превышающих предел прочности материала на сжатие. Поэтому необходимо учитывать эти напряжения в механизме термического разрушения материала. Требуется выяснить, какой вид напряжений достигает раньше своих предельных значений для проводимых тепловых потоков.

Рассмотрим свободную со всех сторон пластинку толщиной 2δ. К поверхности z=+δ, начиная с момента времени τ=0, подводится постоянный удельный тепловой поток. Нижняя поверхность z=-δ и боковые края пластины – теплоизолированы.

Уравнение теплопроводности с граничными и начальными условиями запишется в виде:

a ^ = ^ Т ст ^d z       ^{d T}

;

(1.1)

Т = 0, T 0;

Я дТ = q, z = +5; rW ст z д Т

Я — = 0, z = —5. ^, ст z

Распределение температуры по толщине зависит от теплофизических свойств материала, величины теплового потока и времени его подачи [2].

Т ( - ;5 ) = q {--- ^V--- t+

5        2( с рЯ ) ст

Я

3 z / 5 + 6 z / 5 - 1 —

12 v

^       .n                     2 2

4 V ( — 1)         2 n v         n n z

—Г L- —2-exp [ — n -------T ]cos[ — (- +1)]},

П vn=1   n            4(СрЯ)ст        2 5     ( v= _ст.

Зная распределение температуры в пластине, вычисляют термические напряжения растяжения и сжатия, возникающие в некоторый момент времени τ на различной глубине от поверхности δ i (δ=z i ) при данном значении теплового потока q. Пластина с переменной по толщине температурой находится в плоско напряженном состоянии. Напряжения определяются по уравнению:

о = о xx      yy

+5

e t E z           1             z

(1.3)

= ^- 0- д )" T ⁽ 5^T ) + (1 - д )2 5 I ^{е ET (} 5 ^;T ) dz’

-5

где первый член - составляющая напряжения сжатия, а второй - растяжения; вгкоэффициент линейного расширения; Е - модуль Юнга.

Задаваясь предельными значениями напряжения сжатия и растяжения для каждого материала, получают функциональную зависимость теплового потока, вызывающего разрушение, от времени подачи и глубины проникновения. Кроме того, приравнивая температуры на поверхности пластины к температуре плавления металла, находят значения удельных тепловых потоков, необходимых для расплавления поверхностного слоя за различный промежуток времени их действия. Таким образом, в каждом конкретном случае имеют функциональные зависимости теплового потока от времени воздействия его на конструкционную поверхность:

• -    плавление поверхности пластины:

^

q 1 = Т пл /{---- ^v---т+ — - -2- - S ⁽—2-exp[ - ( n nv )² т / 4( c pX ) ct ]cos n n }; (1.4)

2(cpX)cT    3 v n v n=i

• -    создание предельных напряжений сжатия:

  q 2

  
  

. (1 - д)о пр. сж /{ V т + 3z2 / 52 + 6z / 5-1 PtE      2( cpX) ct12

(1.5)

+ 1)]};

(1.6)

-^r - S(-12-exp [-(nnv)2 т/ 4(cpX)CT]cos[n^ (-n v n=1  n2

- создание предельных напряжений растяжения

(1  Р)°пр. pac / etE     2(cpX)ct T

Для расчета выберем пластину из меди, функциональные зависимости q1, q2 и q3 были рассчитаны для таких материалов, как медь и нержавеющая сталь. Термомеханические характеристики для данных материалов представлены в таблице 1.1 [3].

Таблица 1. 1 – Термомеханические свойства меди и нержавеющей стали

Материал	ρ Кг/м3∙103	β 1/К∙10-5	С Дж/кг∙с	0 пл,	μ, Па∙с	Е, Н/м2∙10	σ пр.р Н/ м2∙10	σ пр.ст Н/ м2∙10
Медь	8,9	1,6	390	1100	0,34	11,8	220	1570
Нержавеющая сталь	7,8	1,1	516	1300	90,35	21,6	700	2500

Результатами расчетов явились аппроксимические зависимости тепловых потоков, вызывающих напряжения сжатия и растяжения меди в зависимости от времени действия их воздействия. Полученные зависимости представлены на рисунке 1.

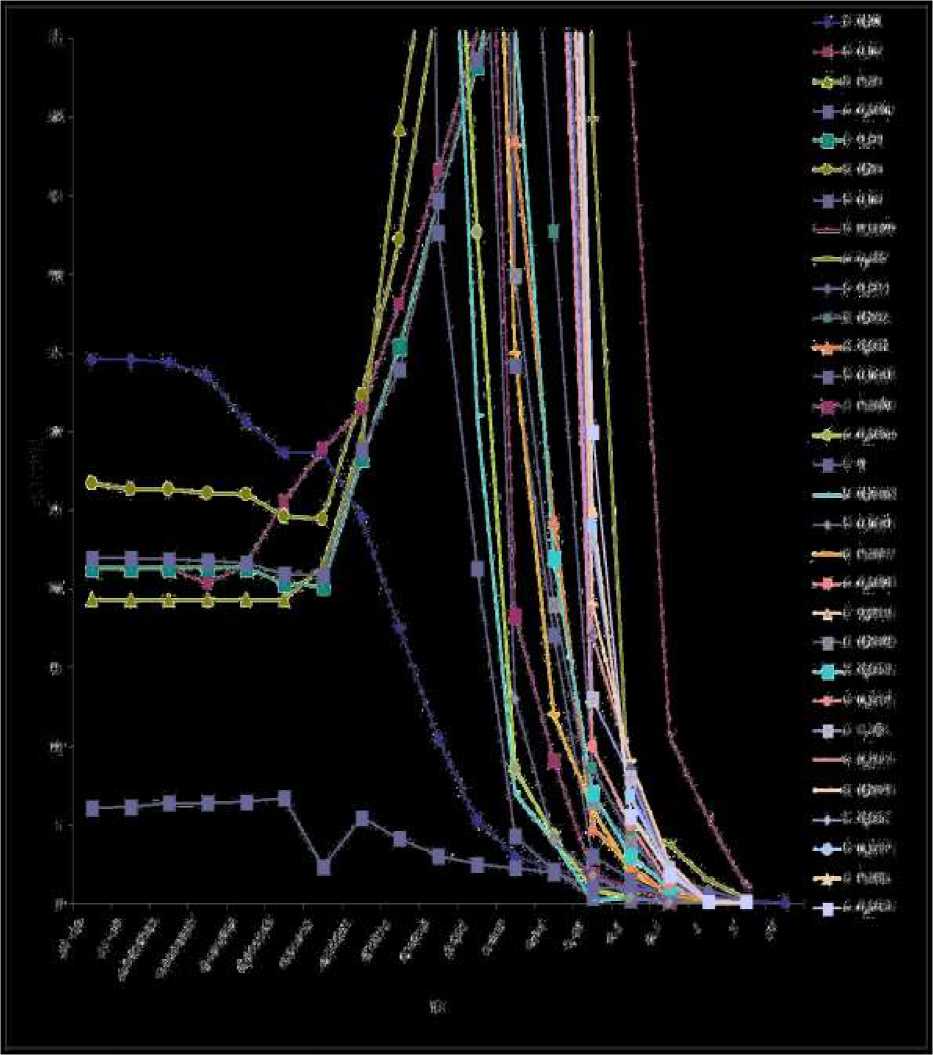
Рис. 1. - Зависимость тепловых потоков, вызывающих напряжения сжатия и растяжения металлов в зависимости от времени действия для различной величины критической трещины. [4]

Таким образом, приведенные зависимости наглядно показывают, что увеличение теплового потока в местах концентрации напряжений негативно влияют на теплофизические свойства материала, что может привести к их разрушению в период нестационарной работы турбоагрегата.