Влияние учета межкомпонентного взаимодействия на параметры течения газа при математическом моделировании истечения газовзвеси в вакуум

Течения неоднородных сред встречаются как в естественной природе, так и в технике. В ряде монографий представлена методология моделирования течения многофазных сред и смесей, в которых компоненты имеют различное агрегатное состояние, в том числе газовзвесей – аэрозолей и запыленных сред [4; 6; 14; 15]. Теоретическому и экспериментальному исследованию динамики газовзвесей посвящены публикации в периодических изданиях [1; 2; 3; 7; 8; 10; 11; 12; 13; 18; 19; 20]. В работе [8] математически моделируется и экспериментально исследуется оптимизация технологического процесса, связанного с динамикой дисперсных потоков. В работе [1] аналитически моделируется процесс аспирации в двумерной области без учета взаимообратного влияния несущей и дисперсной среды; предполагается, что динамика дисперсной компоненты не оказывает влияние на движение несущей среды. Одновременно с этим на данный момент является актуальным исследование влияния компонентов смеси на динамику потока неоднородных сред. В данной работе исследуется влияние дисперсной компоненты на течение двухфазного потока. Необходимость подобных теоретических исследований для промышленности связана с тем, что наличие дисперсных включений оказывает значительное влияние на характер процессов и рабочие характеристики устройств, в которых используются потоки неоднородных сред.

Динамика однородного вязкого газа в одномерном приближении описывалась системой уравнений, включающей в себя уравнение сохранения массы (1), уравнение Навье – Стокса (2) и уравнение сохранения полной энергии (3) для сжимаемого теплопроводного газа:

Тукмаков Д.А. Влияние учета межкомпонентного взаимодействия на параметры...

5Р+^(Р^) = 0;(1)

d tд

^ + 3p и2 + р-т)- F + «|р;(2)

d t    d x            ’

д ( e ) д 3        . , д T ) _ , ,z х     f д ( ри ) )

"ЗТ" ’.ill e+р-т]U+хз~ 1= Q - F 1(U - и1)-a         , д t d x V              дx )                    V д x )

Т = ⁴ g^ u , T = ( y- i ) ( e / p- 0,5 и ² ) / R .

• 3 о x

В работе используются следующие обозначения: p , ρ , u – соответственно давление, плотность, скорость газа; Т , е – соответственно температура и полная энергия газа. В уравнениях динамики неоднородной среды индексы 1 и 2 относятся соответственно

• к несущей и дисперсной компонентам смеси.

Динамика аэрозоля описывается системой уравнений (4)–(9), включающей в себя системы уравнений движения несущей и дисперсной фаз смеси с учетом межфазного взаи- модействия:

dPi , d(piUi) = 0 d td

^+3piu" + p-t)-F +«£, d t d x             '

“(e1)+ 3“f[ e 1+ P-T] Ui +^дТ' ^=- Q - F К ui-u 2 )-a ^(pu1) ;(6)

a t   a x V                a x )                     V a x )

3p2 +dpu) = 0, d t fc) +^(p, u,2 ) = F-a|P;(8)

д t     д xд

^(e2) + 3 e 2 и 2 ) = Q;(9)

д tд p2 =ap20; e 2 =p2 CPT2 ;

3a                                 f d u1d

^F S = ( 8 r ) C d ^{p U} 1 - ^U 2 ^{( U} 1 - ^U 2 ^{) ; F}A =^ap i V d t ^{+ U} 1 d x ) ;

^Fam = ⁰ ,5 ^ap 2

dU,     dU,

1 + Ui  1 - d t      dxd

-

u ₂

d U 2_' ; d x )

F = F_s + F a + F am ; Q = 6aNu Л( T , - T ₂)/(2 r )²;

C = ⁴⁴ + ^d Re₁ Re₁ ^0,5

+ 0,4;

M i = | ^U i ^{- U} 2| / c ; Re _i =p _i | u _i - U 2| 2 r / g ; Pr = C g / X .

54 в ыпуск 3/2020

Силовое взаимодействие несущей и дисперсной фазы учитывает силу Стокса F_S , силу Архимеда F_A и силу присоединенных масс F_am . Математическая модель предполагает мо-нодисперсный состав дисперсной фазы газовзвеси – все частицы имеют одинаковый размер и одинаковые физические свойства материала. В уравнении используются обозначения С_р – удельная теплоемкость единицы массы вещества, из которого состоят частицы; r – радиус частицы; λ и μ – соответственно коэффициенты динамической вязкости и теплопроводности газа; γ и R – соответственно постоянная адиабаты и газовая постоянная воздуха; τ – тензор вязких напряжений газа в одномерном случае. Число Нуссельта определяется с помощью известной аппроксимации в зависимости от относительных чисел Маха, Рейнольдса и Прандтля [14]:

Nu₁ = 2exp( - M 1 ) + 0,459Re 0^,55 Pr ^0,33 .

Система уравнений движения двухфазной монодисперсной смеси в матричном виде имеет вид

q * + E , = H , (10)

q = [ P 1 , ^P 2 , ^P 1 u 1 , ^P 2 u 2 , e l , e 2 ^] ;

E =

^p i u i

^P 2 u 2

(Pl Ui2 +p — T)

^p 2 ^U 2

((e1 + p — t) u1 — XdT/d x)

e ₂ u ₂

— F + ad ( p ₁ u ₁)/ d x

F — ad ( p ₁ u ₁)/ d x

— Q — F |( u ₁ — u ₂ ) + ad ( p ₁ u ₁)/ d x

Q

Система уравнений (10) решалась явным методом Мак-Кормака второго порядка [17]. Явная схема Мак-Кормака включает в себя последовательно выполняемые шаги (11) и (12):

• ^q := ^q ■ —£ ( e ‘^1 — e ' ) +^a * ^H nj ;                    ^ai)

q j *' = 0,5( q j + q ,¹) — 0,5 ^- ( E j — E^, ) + 0,5 A * H j .            (12)

Здесь Δ t , Δ x – соответственно шаги по временной и пространственной координатам; j , n – соответственно индекс узлов по координатам х и t.

Алгоритм явного конечно-разностного метода Мак-Кормака дополнялся схемой коррекции сеточной функции, позволяющей преодолеть численные осцилляции [5; 9].

При моделировании динамики неоднородной среды задавались следующие граничные условия [14]:

u ₁ ( * ,1 ) = 0, u ₂ ( * ,1 ) = 0 ;

e 1 ( * ,1 ) = e 1 ( * ,2 ) , e 2 ( * ,1 ) = e 2 ( * ,2 ) ,

• p 1 ( * ^,1 ) = p 1 ( * ,2 ) , p 2 ( * ^,1 ) = p 2 ( * ,2 ) .

Тукмаков Д.А. Влияние учета межкомпонентного взаимодействия на параметры...    55

u 1 ( t , N ) — u 1 ( t , N — 1 ) , u 2 ( t , N ) — u 2 ( t , N — 1 ) , e i ( t , N ) — e i ( t , N — 1 ) , e 2 ( t , N ) — e 2 ( t , N — 1 ) ,

P i ( t , N ) = P 1 ( t , N — 1 ) , P 2 ( t,N ) = P 2 ( t,N — 1 ) .

В начальный момент времени компоненты смеси покоились:

u 1 ( 0, i ) = 0, u 2 ( 0, i ) = 0.

Для всех искомых функций в моделируемой области течения задавались начальные значения:

⁽ x <  L ^/2): e 1 ⁽ 0, i ) — e 10 , e 2 ⁽ 0, i ) — e 20 , ^p 1 ⁽ 0, i ) = ^p 10 , ^p 2 ⁽ 0, i ) = ^p 20 ;

( x >  L /2): e 1 ( 0, i ) — 0, e 2 ( 0, i ) — 0, P 1 ( 0, i ) — 0, P 2 ( 0, i ) — 0.

Численное решение проводилось на равномерной сетке с количеством узлов N = 1000 вдоль оси x . Алгоритм численного решения системы уравнений математической модели был реализован на языке Fortran.

Компьютерная реализация численной модели имеет следующею структуру:

• 1)    блок задания начальных значений параметров смеси;

• 2)    подпрограмма вычисления межфазного силового взаимодействия и теплообмена;

• 3)    подпрограмма численного решения.

Вычисление значений параметров компонент газовзвеси на каждом последующем временном слое осуществляется последовательным применением шагов 2, 3.

Начальное объемное содержание вещества дисперсной фазы α = 0,001; физическая плотность вещества дисперсной фазы ρ ₁₀= 2500 кг/м³; радиус частиц r = 10 мкм; начальное давление и температура газа p = 98 кПа и T = 293 K; L = 1 м.

На рисунке 1 представлено схематичное изображение канала, из одной части которого откачен газ.

Рис. 1. Схематичное изображение канала с запыленной средой

Результаты численных расчетов давления газа в процессах истечения в вакуум различных сред представлены на рисунке 2.

За счет межфазного взаимодействия процессы в вязком газе и в вязком газе с дисперсной компонентой волны давления имеют различную скорость движения и различный

Выпуск 3/2020

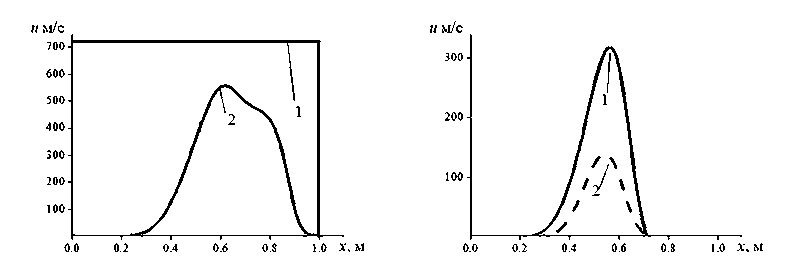
профиль. Сопоставление максимальной скорости потока невязкого газа (724 м/с) в аналитическом решении [16] (кривая 1 ) с численным решением максимальной скорости потока (560 м/с) однородного вязкого газа (кривая 2 ) показывает (рис. 3- а ), что учет вязких напряжений в математической модели уменьшает рассчитанную скорость движения среды. Вычисленная скорость потока вязкого газа при распространении запыленной среды в вакуум (рис. 3- б , кривая 1 ) достигает максимального значения 317 м/с за время меньшее, чем в однородном газе (рис. 3- а ). При этом скорость потока дисперсной фазы (рис. 3- б , кривая 2 ) в запыленной среде достигает максимального значения 138 м/с, что существенно меньше, чем скорость потока несущей среды газовзвеси (рис. 3- б ).

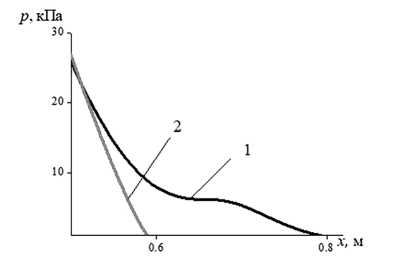
Рис. 2. Расчеты давления газа в процессах истечения в вакуум различных сред: 1 – пространственное распределение давления при разлете в вакуум однородного вязкого газа;

2 – вязкого газа с дисперсной компонентой

б

а

Рис. 3. Пространственное распределение скоростей газа:

а – в аналитическом решении для невязкого газа (кривая 1) и в численном решении для вязкого газа (кривая 2); б – для численных скоростей несущей (кривая 1) и дисперсной (кривая 2) компонент газовзвеси

Наличие межфазного взаимодействия оказывает существенное влияние на процесс разлета газовзвеси в вакуум, за счет чего скорость потока сплошной среды в однородном вязком газе, вязком газе с дисперсной компонентой и скорость потока дисперсной компоненты отличаются друг от друга.

При истечении газовзвеси в вакуум процесс массопереноса дисперсной компоненты смеси (кривая 2 ) более длительный, чем процесс массопереноса газа (кривая 1 ) (рис. 4).

Тукмаков Д.А. Влияние учета межкомпонентного взаимодействия на параметры...    57

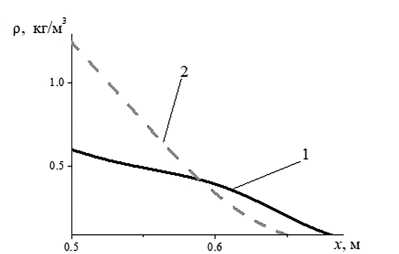
Рис. 4. Длительность процесса массопереноса:

1 – газа; 2 – дисперсной компоненты смеси

Заключение

В данной работе были проведены численные расчеты истечения в вакуум однородной вязкой среды и вязкой среды с дисперсной примесью. Выявлено, что учет математической модели межфазного взаимодействия приводит к тому, что скорость движения несущей среды в смеси имеет меньшее значение, чем скорость истечения однородного вязкого газа.

Численные расчеты показывают, что процесс массопереноса дисперсной компоненты смеси более длительный, чем процесс массопереноса несущей компоненты смеси. Закономерности, полученные в вычислительных экспериментах, можно использовать при разработке и оптимизации аппаратов и промышленных технологий, в которых происходит истечение дисперсного потока в разреженную среду. Сопоставление математических моделей динамики однородного вязкого газа и вязкого газа с дисперсной компонентой показывает существенное влияние учета взаимодействия компонент на динамику всей смеси.