Влияние угла "встречи" фуллерита C60 с подложкой твердого тела на процесс осаждения

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2020PNRPU MECHANICS BULLETIN

Все более широкое практическое применение фуллеренов и фуллеритов в различных отраслях промышленности обусловливает и большой объем научных работ [1–14], посвященных этим соединениям.

При этом исследования, направленные на изучение фуллеренов и фуллеритов, ведутся не только посредством проведения натурных экспериментов, но и с применением компьютерного моделирования, в том числе с использованием аппарата молекулярной динамики [15–17].

В статье [18] приведены результаты моделирования взаимодействия фуллерита C 60 с подложкой железа при различных условиях – температура, скорость движения фуллерита и ориентация фуллерита относительно подложки. Было рассмотрено три варианта положения фул-лерита по отношению к подложке в момент их контакта, а именно – грань, ребро и вершина [18].

Благодаря исследованиям, приведенным в [18], были установлены основные закономерности процесса осаждения фуллерита на подложку железа Fe(100). Однако во всех компьютерных моделях [18] вектор скорости фуллерита был направлен по нормали к плоскости подложки.

В данной работе исследуется влияние угла «встречи» фуллерита C 60 с подложкой.

Следует отметить, что в приведенной работе, как и в работе [18], при моделировании процесса осаждения фуллерит имеет гранецентрированную кубическую (ГЦК) укладку молекул фуллеренов C 60 .

1.    Постановка задачи

Условия моделируемого процесса соответствуют тем, что были приведены в статье [18]:

• –    подложкой твердого тела является кристалл железа Fe(100) с постоянной решетки 2,87 Å [19], а тип его кристаллической решетки – кубическая объемно-центрированная;

• –    постоянная кристаллической решетки фуллерита принята равной 1,4154 нм [14];

• –    при моделировании системы фуллерит С 60 – подложка задавались следующие значения температуры: 300, 700, 1150 К;

• –    фуллерит до контакта с подложкой имел постоянную скорость, ее значения – 0,005; 0,01; 0,02 Å/фс;

• –    расстояние вдоль оси Oz между контактной поверхностью подложки и нижней гранью (1-й слой) фул-лерита С 60 составляет 11,5 Å;

• –    после соприкосновения фуллерена С 60 с подложкой скорость всех атомов системы определяется значением температуры системы.

Отличие от задачи, приведенной в [18], состоит в том, что вектор скорости фуллерита направлялся не по нормали к контактной поверхности подложки, а под углом. Угол «встречи» между фуллеритом и подложкой измерялся как угол между вектором скорости фуллери-та и нормалью к контактной поверхности подложки (кристалла железа Fe(100)), причем вектор скорости и нормаль лежат в одной плоскости, что показано на рис. 1.

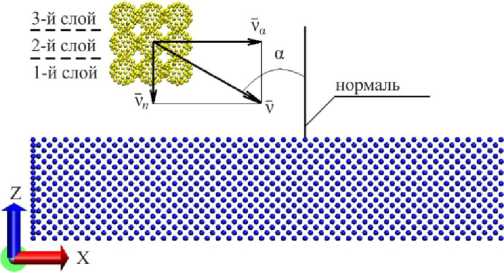
Рис. 1. Угол «встречи» между фуллеритом C60 и подложкой

Fig. 1. The meeting angle of fullerite C 60 and the substrate

При исследовании устанавливались три угла «встречи» ( α ) фуллерита с подложкой – 15°, 45°, 75°.

Для удобства описания и анализа результатов взаимодействия фуллерита C 60 с подложкой введем понятия:

• –    нормальная составляющая скорости фуллерита ( v n ) – проекция скорости фуллерита на нормаль к контактной грани подложки;

• –    тангенциальная составляющая скорости фуллери-та ( v τ ) – проекция скорости фуллерита на плоскость, параллельную контактной грани подложки.

Числовые значения нормальных и тангенциальных составляющих скоростей фуллерита C 60 приведены в табл. 1.

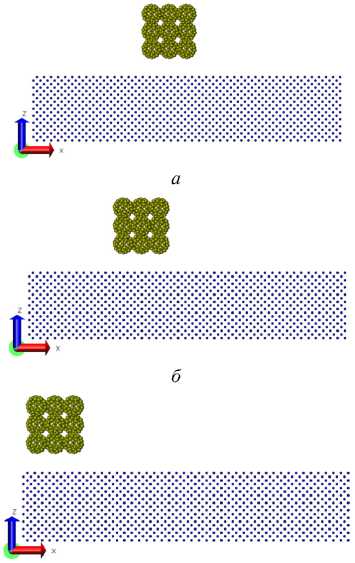
в

Рис. 2. Положение фуллерита С₆₀ и подложки железа в начальный момент времени: а – угол 15°; б – угол 45°; в – угол 75°

Fig. 2. The position of fullerite C₆₀ and the iron substrate at the initial time: a ) the angle – is 15 degrees; b ) the angle – is 45 degrees; c ) the angle – is 75 degrees

Таблица 1

Значения нормальных и тангенциальных составляющих скоростей фуллерита C 60

Table 1

Values of normal and tangential components of C60 fullerite velocities

Показатели	Скорость фуллерита, Å/фс
	0,005			0,01			0,02
Угол «встречи» фуллерита С60 с подложкой, град	15	45	75	15	45	75	15	45	75
Нормальная составляющая скорости фулле-рита ( v n ), Å/фс	0,0048	0,0035	0,0013	0,0097	0,007	0,0026	0,019	0,014	0,005
Тангенциальная составляющая скорости фулле-рита ( v τ ), Å/фс	0,0013	0,0035	0,0048	0,0026	0,007	0,0097	0,005	0,014	0,019

Кинетическая энергия каждого отдельного фуллерена, образующего фуллерит, при скоростях 0,005; 0,01; 0,02 Å/фс соответственно составит: 0,93 эВ, 3,73 эВ, 14,94 эВ.

Состояние системы в начальный момент времени показано на рис. 2.

Фуллерит контактировал с поверхностью подложки гранью.

Продолжительность моделирования процесса взаимодействия фуллерита с подложкой составляла t м = = 60 пс, с шагом по времени Δ t = 1 фс.

Моделирование процесса осаждения фуллерита С 60 на подложку железа Fe(100) велось методом молекулярной динамики [20–26] в программном комплексе LAMMPS [27–35].

2.    Результаты расчетов

Аналогично результатам, приведенным в статье [18], следует отметить, что до удара фуллерита C60 о подложку железа Fe(100) расстояние между фуллеренами, образующими фуллерит, уменьшается.

Количество фуллеренов С 60 , осевших на подложке после удара об нее фуллерита, показано в табл. 2.

Приведенные в табл. 2 значения «14» и «14*» характеризуют:

• –    «14» – после контакта с подложкой железа фуллерит С 60 осел полностью, и его структура осталась целостной.

• –    «14*» – после контакта с подложкой железа фул-лерит С₆₀ осел полностью, но его структура нарушена.

Из результатов, приведенных в табл. 2, следует, что с увеличением скорости фуллерита количество фуллеренов, осевших на подложку железа, уменьшается, а увеличение угла «встречи» ( α ) фуллерита с подложкой, напротив, приводит к увеличению количества осевших фуллеренов, и при определенных условиях наблюдается полное осаждение фуллерита на подложку. Влияние температуры на процесс осаждения фуллерита носит разнонаправленный характер.

Таблица 2

Фуллерены С60, осевшие на подложку

Table 2

C 60 fullerenes deposited on the substrate

Показатели		Скорость фуллерита, Å/фс
		0,005			0,01			0,02
Температура системы подложка и фул-лерит C 60 , К		300	700	1150	300	700	1150	300	700	1150
Угол «встречи» фуллери-та С 60 с подложкой, град	15	5	5	5	5	5	5	5	5	3
	45	14	14*	14*	5	5	5	5	5	5
	75	14	14	14*	14*	14*	14*	–	1	2

Следует заметить, что при определенном сочетании угла «встречи» и скорости фуллерита происходит ри-кошетирование последнего, возможно, это объясняется большим значением v τ .

На рис. 3 показаны результаты моделирования осаждения фуллерита на подложку железа при различных условиях.

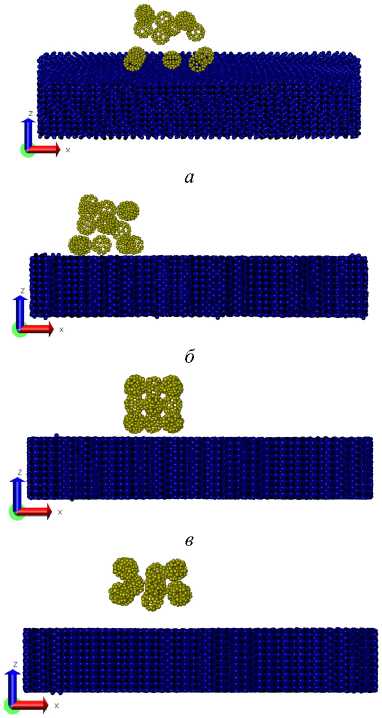
г

Рис. 3. Фуллерит С 60 после взаимодействия с подложкой железа: а – α = 15°, v = 0,01 Å/фс, T = 700 К; б – α = 45°, v = 0,005 Å/фс, T = 1150 К; в – α = 75°, v = 0,005 Å/фс, T = 300 К; г – α = 75°, v = 0,02 Å/фс, T = 300 К

Fig. 3. C₆₀ fullerite after interaction with the iron substrate: а – α = 15 degrees, v = 0.01 Å/fs, T = 700 K; b – α = 45 degrees, v = 0.005 Å/fs, T = 1150 K; c – α = 75 degrees, v = 0.005 Å/fs, T = 300 K; d – α = 75 degrees, v = 0.02 Å/fs, T = 300 K

Для удобства анализа результатов осаждения фул-лерита С 60 на подложку условно разделим ее на три слоя, как показано на рис. 1, и проведем нумерацию фуллеренов (рис. 4).

5                       4             7                   14                      13

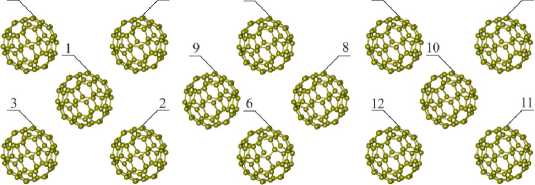
а б в

Рис. 4. Нумерация фуллеренов в фуллерите С 60 : а – 1-й слой; б – 2-й слой; в – 3-й слой

Fig. 4. Numbering of fullerenes in C 60 fullerite: a – 1 layer;

b – 2 layer; c – 3 layer

Фуллерены с «1» по «5» образуют грань, контактирующую с подложкой.

Графическое представление поведения центра масс фуллеренов, осевших на подложке железа, показано на рис. 5–7, где изображены изменения расстояний в процентах от первоначального расстояния между фуллереном «1» и соответственно фуллеренами «2»–«14».

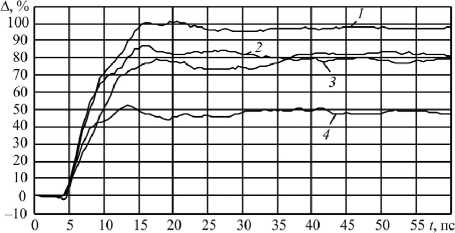
Рис. 5. Поведение фуллеренов, осевших на подложку железа ( α = 15°, v = 0,01 Å/фс, T = 700 К): 1 – «1»–»2»; 2 – «1»–»3»; 3 – «1»–»4»; 4 – «1»–»5»

• Fig. 5.    The behavior of fullerenes deposited on the iron substrate ( α = 15 degrees, v = 0.01 Å/fs, T = 700 K): 1 – «1»–»2»;

2 – «1»–»3»; 3 – «1»–»4»; 4 – «1»–»5»

Из рис. 5 следует, что после удара фуллерита о подложку и осаждения фуллеренов, образующих первый слой фуллерита, на подложке железа наблюдается увеличение расстояния между центральным фуллереном «1» и фуллеренами «2»–«5», достигающего к 15 пс значений, превышающих первоначальные более чем на 40 %, затем фуллерены «2»–«5» начинают занимать квазистационарное положение относительно фуллерена «1». Это существенно отличается от случаев, описанных в статье [18], когда фуллерит контактирует гранью с подложкой, при которых в осевшем на подложке первом слое расстояния между фуллереном «1» и фуллеренами «2»–«5» увеличиваются не более чем на 15 %. Это может объясняться тем, что в приведенной задаче фуллерены имеют составляющую скорости, параллельную контактной поверхности подложки железа.

О 5    10 15 20 25 30 35 40 45 50 55 t, пс

б

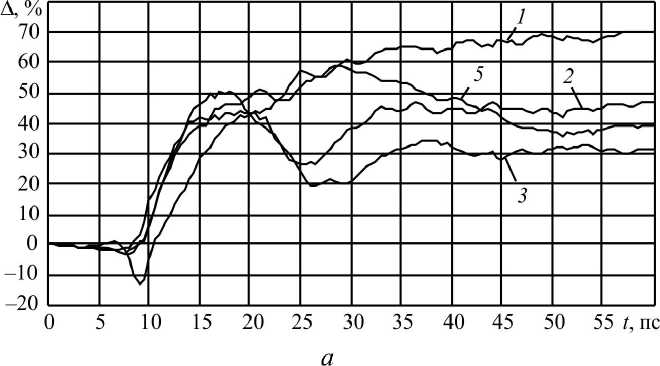
Рис. 6. Поведение фуллеренов, осевших на подложку железа ( α = 45°; v = 0,005 Å/фс, T = 1150 К): а – 1 – «1»–«2»; 2 – «1»–«3»; 3 – «1»–«4»; 5 – «1»–«6»; б – 4 – «1»–«5»; 6 – «1»–«7»; 7 – «1»–«8»; 8 – «1»–«9»; 9 – «1»–«10»;

10 – «1»–«11»; 11 – «1»–«12»; 12 – «1»–«13»; 13 – «1»–«14»

• Fig. 6.    The behavior of fullerenes deposited on the iron substrate ( α = 45 degrees, v = 0.005 Å/fs, T = 1150 K): а – 1 – «1» – «2»; 2 – «1»–«3»; 3 – «1»–«4»; 5 – «1»–«6»; б – 4 – «1»–«5»; 6 – «1»–«7»; 7 – «1»–«8»; 8 – «1»–«9»; 9 – «1»–«10»;

10 – «1»–«11»; 11 – «1»–«12»; 12 – «1»–«13»; 13 – «1»–«14»

В случае, представленном на рис. 6, следует выделить две основные тенденции поведения фуллеренов после контакта фуллерита с подложкой и его осаждения на ней:

• –    резкое увеличение расстояния между фуллереном «1» и, соответственно, фуллеренами «2»–«4» (первый слой) и фуллереном «6» (второй слой), расстояние между центральным и указанными фуллеренами растет до 50 пс, затем наступает этап квазистационарного равновесия;

• –    поведение фуллерена «5» (первый слой) и фуллеренов «7»–«14» (второй и третий слои) носит разнонаправленный характер, но после 40 пс они занимают ква-зистационарное положение, при этом только у фуллерена «12» наблюдается увеличение расстояния между ним и фуллереном «1» на величину порядка 10 %, у остальных фуллеренов к 60 пс расстояние до фуллерена «1» уменьшается.

Таким образом, в случае, представленном на рис. 6, три из четырех фуллеренов первого слоя ведут себя аналогично случаю, приведенному на рис. 5, а большинство фуллеренов второго слоя и все фуллерены третьего слоя практически сохраняют свое первоначальное положение относительно фуллерена «1», что и позволяет сделать вывод о том, что фуллерен осел полностью, но его структура после удара нарушена.

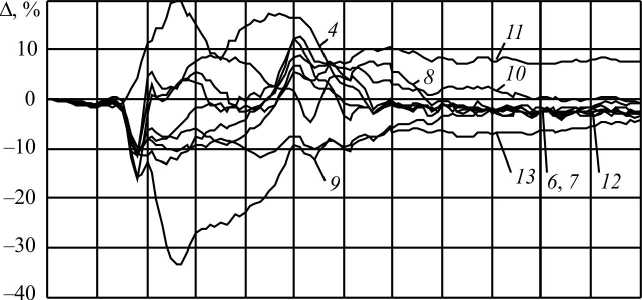
Рис. 7. Поведение фуллеренов, осевших на подложку железа ( α = 75°; v = 0,005 Å/фс, T = 300 К): 1 – «1»–«2»; 2 – «1»–«3»; 3 – «1»–«4»; 4 – «1»–«5»; 5 – «1»–«6»; 6 – «1»–«7»; 7 – «1»–«8»; 8 – «1»–«9»; 9 – «1»–«10»; 10 – «1»–«11»;

11 – «1»–«12»; 12 – «1»–«13»; 13 – «1»–«14»

Fig. 7. The behavior of fullerenes deposited on the iron substrate ( α = 75 degrees, v = 0.005 Å/fs, T = 300 K): 1 – «1»–«2»; 2 – «1»–«3»; 3 – «1»–«4»; 4 – «1»–«5»; 5 – «1»–«6»; 6 – «1»–«7»; 7 – «1»–«8»; 8 – «1»–«9»; 9 – «1»–«10»;

10 – «1»–«11»; 11 – «1»–«12»; 12 – «1»–«13»; 13 – «1»–«14»

В случае осаждения фуллерита на подложку, показанного на рис. 7, фуллерены «2»–«6» начинают увеличивать свое расстояние до фуллерена «1», а у остальных фуллеренов, напротив, наблюдается сокращение расстояния до центрального фуллерена, но с 35 пс расстояние от каждого из фуллеренов до фуллерена «1» начинает постепенно возвращаться к первоначальному, а с 50 пс происходит скачкообразное возращение фуллеренов к исходному положению относительно фуллерена «1». Дальнейшее изменение расстояний носит очень малый характер и связано, скорее всего, с температурными флуктуациями.

Проводя анализ результатов компьютерного моделирования, приведенных в данной статье, следует обратить внимание и на результаты натурного эксперимента, приведенного в работе [36]. Так, в [36] исследовалось осаждение фуллеренов C 60 импульсным сверхзвуковым молекулярным пучком (СМП) на подложки различных металлов и оксидов. Для формирования СМП использовались инертные газы аргон (Ar) и гелий (Не), которые обогащались фуллеренами C 60 , а затем СМП проходил через скиммер, «выделяющий осевую часть потока, за которой располагалась подложка» [36]. В работе [36] не указано, под каким углом к СМП устанавливалась подложка. Однако даже если СМП подавался по нормали к контактной поверхности подложки, ввиду неизбежной турбулизации СМП у какой-то части фуллеренов при контакте с подложкой вектор скорости был направлен под углом ( α ) к нормали, отличным от нуля. Таким образом, можно утверждать, что часть фуллеренов, образующих пленку C 60 [36], особенно фуллерены, находящиеся в периферийной зоне пленки, осаждались по механизму, схожему с тем, что описан в данной работе.

Выводы

Из полученных результатов моделирования осаждения фуллерена на подложку железа при различных углах «встречи» можно сделать следующие выводы:

• 1.    Угол «встречи» фуллерита С 60 с подложкой железа оказывает существенное влияние на процесс его осаждения; так, при угле «встречи» фуллерита С 60 с подложкой железа в 15° осаждается только первый слой фуллерита С 60 , что схоже с результатами взаимодействия, приведенными в [18], где вектор скорости фуллерита направлялся по нормали к подложке, а при углах «встречи» 45° и 75° и скорости 0,005 Å/фс наблюдается полное осаждение фуллерита на подложку, при этом в отдельных случаях структура фуллерита может сохраняться.

• 2.    В отличие от случаев, описанных в статье [18], в данной работе показано, что при осаждении на подложку железа фуллеренов первого слоя в основном наблюдается существенное увеличение расстояния