Влияние углов ориентации слоя на толщину несущих панелей из слоистого композита

Для летательных аппаратов проблема снижения веса элементов конструкции исключительно актуальна. Один из путей решения этой проблемы – использование слоистых композиционных материалов, обладающих высокими прочностными характеристиками [1–3].

Однако при проектировании тонкостенных несущих панелей несущая способность в большей степени определяется устойчивостью, которая сильно зависит от укладки. Например, для прямоугольной неподкрепленной панели длиной 500 мм, шириной 250 мм и укладкой [45/0/0/0/0]s критическая нагрузка составляет 131 кгс, а для укладки [0/0/0/0/45]s – 76 кгс, что в 1,7 раза ниже.

Существующие алгоритмы имеют ряд недостатков: одни алгоритмы дают только процент-

ное содержание слоев и необходимую толщину по прочности [4–6], тогда как изменение положения слоя в укладке может привести к изменению изгибных жесткостных характеристик в несколько раз, что решающим образом влияет на несущую способность по устойчивости; в решениях для подкрепленных панелей часто используется эффективная жесткость [7], что некорректно отражает работу стрингеров, поскольку не учитывает их работу при изгибе из плоскости при совместном деформировании с панелью. В задачах рационального проектирования это обстоятельство фактически исключает возможность корректного определения оптимальной высоты стрингерного набора.

Авторами разработан алгоритм выбора рациональных параметров (АВРП) неподкрепленной и стрингерной композитных панелей минимального веса, нагруженных продольным, поперечным и сдвиговым потоками при ограничениях по прочности и устойчивости [8, 9]. Для ускорения работы АВРП получены аналитические решения задач

Том 8

устойчивости неподкрепленной и стрингерной композитных панелей при граничных условиях опирания и защемления, которые позволяют учесть дискретность расположения стрингеров для подкрепленных панелей и изгибно-крутильную потерю устойчивости стрингера, которая реализуется при избыточном увеличении высоты стрингерного набора. В отличие от алгоритмов, предлагающих только определение необходимого процентного соотношения слоев по прочности, созданный алгоритм дает возможность получить полную последовательность слоев в пакете.

Цели работы: проверка несущей способности образцов, по лученных с помощью АВРП; вали дация расчетных моделей; оценка влияния углов ориентации слоев на толщину и несущую способность панелей из слоистого композита.

1. Алгоритм выбора рациональных параметров панелей из слоистого композита

В качестве критерия прочности пакета использован принцип непревышения принятого предельного уровн я и нтенсивности деформации.

Интенсивность деформации определяется из известных соотношений теории упругости для ортотропно й з адачи [10]

* i = f^ -. ) 2 ₊ (,-.) ² +, 1 -S ₃ ) ^{2 +} 2 ,22 ,⁽¹⁾

£1 = a-V2.i  *2=£l-v,A

¹    E 1² E 2²    E 2¹ E 1

Y ₁₂ =—, e ₃ =-v ₃ G

a, a

^E 1 ^E

,

E

^{V 1} = E; ^{2 ,}

П о дставив (2) в (1 ) и выразив толщину h , получим:

* =    • vF, i 3 • h v i

где

Fi =

₃-Vj ) ² + (1 + v₃ ) ² ) + 31     3

₊l q

E 2 7

• ( (1 ₊ v 2 ) + (1 + v ₃ ) + ⁽ v ₃

V )2 ) +

+2 ■ qf ■ q-•( 2-v2 + 2-V3-(Vi + v 2 ).(V3 + 2)-1) +

EE

+ 3 J q a

2 I G

.

Здесь ε – линей ны е деформации, γ – сдвиговая деформаци я, σ – нормальные напряжения, τ – касательные напряжения, E – модули упругости, G – модуль сдвига, q – потоки. Индексом 1 обозначено направл ен и е п о длине панели, 2 – по ширине панели, 3 – по толщине панели, 12 – сдвиг в плоскости панели. Погонная сила q_d выражается через поток q_d = q ₁1( 1 + h s • ( n s + 2) • B ^-1). Толщина пакета h , не обходимая для обеспечения прочнос т и, определ яет ся из ра ве н ств а интенсивности деф о рмаци и (3 ) предельному значению ε ib .

В ы ражение для определения фактора п отери устойчи во сти п ол учено с п омощ ью энерге тич еского принципа [11]

П = U — X. A = 0 (5) , где U – потенциальная энергия деформации изгиба панели, A – работа внешних сил, λ – фактор критической нагрузки потери устойчивости.

При по лучении в ыраж ений для энергии деформации обшивки и стрингеров предполагалось , чт о изгиб обшивки происходит в рамках гипотезы п лоских сечений с постоянным сдвигом по толщине, а стрингеры деформируются как балки высокого профиля с постоянным сдвигом по в ысоте [11] и, помимо этого, изгибаются из своей плоскости и закручиваются как удлинен ны е пластины, сопряженные одной стороной с о бш и вк ой по прогибам и углам поворота. По высоте стрингера угол поворота сечения считает ся п ост оянным. Укладки для панели и стри н геров в данном случае одинаковы.

В общем виде выражение для определения фа к тора нагрузки потери устойчивости принимает вид

Л — qi-a2 • kn

_ h_s • n s

1 +

B

str

где

U о

-

h

h ²

• 1 + ^ • Sc +   •Ss

B

,

+

+ q ₂ ф₂ • km + q ₁₂ • R • k

D_n .a 4 • kn + D 22 Ф4 • km + 2 • D 3 •« 2 Ф2 -

ao ₁₂ • ao ₃₃ + ao ₁₃ • ao ₂₂ - 2 • ao ₁₂ • ao ₁₃ • ao ₂₃

ao 22 • ao 33 - ao 23

hs-a 4    En • h •Sc •Se

U =                    +

3• B 11 £*• E11 •g2• hs

G

, I _      ^as 12 • as 33 ^{+ a}s 13 • as 22 ^{- 2} • ^as 12 • ^as 13 • as 23

⁺ l ^aS 11                                     2

I                      as 22 • ^as 33 ^{- as} 23

• h--Ss.

B

U_o – энергия деформации изгиба обшивки, U_str – энергия деформации изгиба стрингеров, α₂, α₄, β₂, β₄, ao , as и др. – параметры, зависящие от жесткости, размеров и условий закрепления панели (рассмотрены случаи опирания и защемления по контуру). Выражения для них не приведены ввиду громоздкости. Приравняв к нулю высоту или количество стрингеров, можно получить выражение для неподкрепленной панели.

Для верификации аналитических решений проводилось сравнение критических нагрузок потери устойчивости с результатами конечноэлементного анализа. Получены удовлетворительные результаты. Более подробный анализ приведен в [8].

АВРП включает следующие шаги:

Шаг 1. Формирование пакета минимального веса по прочности

Задается базис, состоящий из набора принятых типичных направлений монослоев, например, 0°, ±45°, 90°.

Задается начальная высота и количество стрингеров.

Принимается пакет из произвольного количества слоев с произвольной укладкой. В двойном цикле по слоям и направлениям базиса каждый слой заменяется направлением из базиса с вычислением толщины с помощью выражения (3). Обычно при этом происходит некоторое изменение толщины пакета. Исследуемому слою присваивается то направление, которое обеспечило наименьшую толщину. После нескольких циклов толщина неизбежно перестает меняться, следовательно, цель достигнута – установлено процентное соотношение направлений слоев, отвечающее комбинации приложенных нагрузок.

При фиксированном количестве монослоев полученное изменение общей толщины приводит к изменению толщины монослоя. Однако на первом шаге корректировка количества слоев не проводится.

Важно отметить, что цель достигнута в результате прямой минимизации веса.

Шаг 2. Формирование пакета минимального веса по устойчивости Укладка и толщина панели, полученные на первом шаге, задаются в качестве начальных для определения фактора потери устойчивости λ по соотношению (6). Если λ ≥ 1, это означает, что полученная укладка обеспечивает помимо прочности еще и устойчивость, т.е. задача решена. Если λ < 1, это означает, что комбинация действующих нагрузок превышает критический уровень, толщина панели увеличивается до нового значения, отвечающего равенству λ = 1, с помощью соотношения, следующего из (6):

h_m8 = hr •                  (7)

нов .

к

Здесь h и λ – значения, полученные по результатам шага 1, и всегда h _нов. ≥ h .

В дальнейшем в двойном цикле по направлениям базиса и по слоям укладки каждый слой последовательно обменивается своим направлением со всеми остальными слоями с одновременным определением толщины по выражению (7) и проверкой по прочности. Из всех опробованных сочетаний направлений выбирается сочетание, соответствующее наименьшей толщине и удовлетворяющее ограничению по прочности. Циклический процесс продолжается до подходящего установления значения толщины.

Как видно, в данном случае осуществляется прямая минимизация веса, но уже с учетом обеспечения устойчивости и прочности.

Шаг 3. Дискретизация

На данном шаге корректируется количество слоев укладки с учетом реальной толщины монослоя и полученной общей толщины.

После дискретизации задается новое значение высоты и/или количества стрингеров, и шаги 1–3 повторяются до установления параметров, соответствующих минимальному весу панели.

Шаг 4. Максимизация мембранной жесткости

В результате дискретизации на шаге 3 за счет округления неизбежно происходит небольшое увеличение общей толщины, что приводит к некоторому небольшому превышению ограничений по прочности и устойчивости. Однако полученное в результате превышение оказывается определяющим, так как позволяет сменить целевую функцию и перейти от минимизации веса к максимизации мембранной жесткости при соблюдении ограничений по устойчивости.

На данном шаге фиксируется количество слоев и в цикле по направлениям базиса и по слоям укладки выбирается укладка, дающая наименьшую интенсивность деформации при соблюдении ограничения на устойчивость.

Шаг 5. Формирование сбалансированной укладки Известно, что при несбалансированной укладке пакета на этапе изготовления может произойти искривление панели. Для того чтобы скорректировать пакет, полученный на шаге 3 и/или 4, с учетом ограничения на сбалансированность в цикле по слоям пакет подбирается так, чтобы в половине симметричного пакета (от края до плоскости симметрии) слоев с направлением 45° было четное количество.

Алгоритм реализован в качестве консольного приложения. Получен сертификат о государственной регистрации программы для ЭВМ [9].

2.    Результаты испытаний образцов стрингерных панелей

Для валидации расчетных моделей были проведены испытания образцов стрингерных панелей из препрега ACM102-C130UD (таблица 1) с укладками трех типов: укладки первого типа получены в результате работы АВРП (обозначение – О4);

²³⁶ укладки второго типа имеют следующее процентное соотношение слоев: 50 % слоев с направлением 0°, 40 % слоев с направлением ±45° и 10 % слоев с направлением 90° (обозначение – О5), такое соотношение обычно рекомендуется для крыльевых силовых панелей; укладки третьего типа

Том 8

получены в результате работы АВРП и скорректированы с учетом ограничения на сбалансированность (обозначение – О6).

Схема образца стрингерной панели представлена на рисунке 1.

Укладки образцов представлены в таблице 2.

Для анализа напряженно-деформированного состояния образцов были разработаны их конечноэлементные модели (КЭМ) совместно с оснасткой для испытаний. Схема и КЭМ образца и оснастки представлены на рисунке 2.

Критические силы стрингерных образцов, полученные при моделировании образца в стенде P _кр.^стенд., разрушающая нагрузка при испытаниях P _разр. и различие между этими силами δ_ст. представлены в таблице 3. Знак «–» в таблице 3 означает, что нагрузка в эксперименте меньше, чем нагрузка в КЭМ.

Таблица 1

Механические характеристики материала ACM102–130UD

E 1, кгс/мм2	E 2, кгс/мм2	E 12, кгс/мм2	μ	t с . , мм	γ, кг/мм3
12882	1059	490	0,34	0,13±0,02	1,55∙10–6

Примечание: E ₁ – модуль упругости монослоя в направлении нулевого слоя, E ₂ – модуль упругости монослоя в поперечном направлении, E ₁₂ – модуль сдвига монослоя, μ – коэффициент Пуассона, t _{с .} – толщина монослоя, γ – плотность.

1000 мм

Рисунок 1. Схема образца стрингерной панели

Таблица 2

Параметры образцов стрингерной панели

Тип	h , мм	h стр , мм	Укладка
О4*	2,34	22	[45/(0) 8 ] s
О5	2,34	27	[45/90/ –45/0/0/0/45/0/0] s
О6**	2,34	22	[±45/(0) 7 ] s

Примечание: * – оптимизированная укладка, ** – оптимизированная и сбалансированная укладка

Таблица 3

Критические силы стрингерных образцов

Тип	P разр. , кгс	P кр. стенд. , кгс	δ ст. ,%
О4(1)	15760	22467	–42,60
О4(2)	21000	23146	–10,20
О5(1)	28300	29131	–2,90
О5(2)	28700	29131	–1,50
О6(1)	25500	23263	–9,60
О6(2)	21700	23263	–6,70

Получено хорошее соответствие расчета с экспериментом. Исключением является только образец О4(1), который имел ярко выраженное коробление.

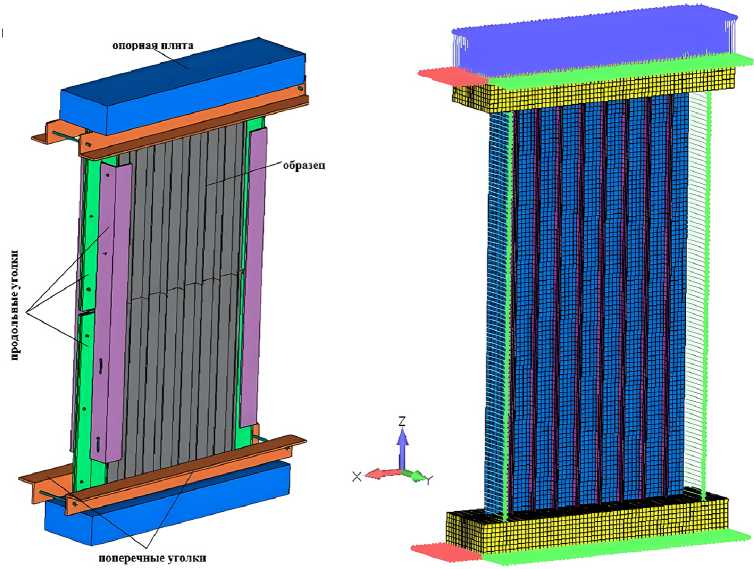
Рисунок 2. Конечно-элементная модель и схема оснастки для испытаний образцов стрингерных панелей

3.    Исследование влияния углов ориентации слоя в укладке на толщину панели

Помимо классического базиса возможных углов ориентации слоев в пакете {±45°;90°;0°} в некоторых источниках используют углы армирования ±15°, ±30°, ±60° и ±75° [12, 13].

С помощью АВРП были получены укладки для неподкрепленной и стрингерной панелей из ACM–C 130UD (таблица 1) с различными базисами:

Базис 1 – {±15°;90°;0°};

Базис 2 – {±30°;90°;0°};

Базис 3 – {±45°;90°;0°};

Базис 4 – {±60°;90°;0°};

Базис 5 – {±75°;90°;0°}.

В таблицах 4 и 5 представлены габариты, нагрузки и полученные укладки для неподкреплен-ной панели.

Таблица 4

№ баз.	h , мм	Укладка	ε i ,%	λ
qx = –50 кгс, qy = 0, L = 800 мм, B = 600 мм.
1	10,14	[(90) 9 /(±15) 5 /0/(±15) 2 /15/(0) 15 ] s	0,037	1,00
2	9,88	[30/90/–30/(90) 2 /30/90/–30/90/0/90/30/90/–30/90/(±30) 2 /90/(0) 17 ] s	0,044	1,01
3	9,10	[(±45) 6 /(90) 2 /(±45) 2 /90/(±45) 4 /45/(0) 7 ] s	0,114	1,00
4	9,62	[(±60) 5 /90/(0) 4 /90/(0) 5 /60/(0) 6 /90/(0) 8 ] s	0,046	1,00
5	10,14	[(±75) 3 /(90) 4 /(0) 29 ] s	0,035	1,00
qx = –50 кгс, qy = –10, L = 800 мм, B = 600 мм.
1	11,18	[(90) 10 /0/(±15) 8 /15/0/–15/(±15) 4 /(0) 5 ] s	0,027	1,00
2	10,66	[(90) 5 /30/90/–30/90/30/90/–30/±30/90/(±30) 2 /30/0/–30/(±30) 6 /(0) 7 ] s	0,043	1,00
3	10,14	[(±45) 8 /45/(0) 2 /–45/90/(±45) 3 /45/0/–45/45/(90) 2 /–45/0/90/(0) 3 ] s	0,083	1,00
4	10,14	[(±60) 8 /60/0/–60/0/90/0/(90) 2 /0/90/0/90/0/90/0/90/(0) 7 ] s	0,071	1,00
5	10,92	[(±75) 7 /(0) 28 ] s	0,029	1,02

Примечание 1: q_x – продольный сжимающий поток, q_y – поперечный сжимающий поток, L – длина панели, B – ширина панели, h – толщина панели, λ – фактор потери устойчивости.

Том 8

Укладки неподкрепленной защемленной панели при различных базисах

Таблица 5

№ баз.	h , мм	Укладка	ε i ,%	λ
qx = –50 кгс, qy = 0, L = 800 мм, B = 600 мм.
1	7,54	[90/(0) 2 /90/(0) 12 /90/(0) 12 ] s	0,041	1,01
2	7,54	[90/(0) 2 /90/(0) 12 /90/(0) 12 ] s	0,041	1,01
3	7,54	[90/(0) 2 /90/(0) 12 /90/(0) 12 ] s	0,041	1,01
4	7,54	[90/(0) 2 /90/(0) 12 /90/(0) 12 ] s	0,041	1,01
5	7,54	[90/(0) 2 /90/(0) 12 /90/(0) 12 ] s	0,041	1,01
qx = –50 кгс, qy = –10, L = 800 мм, B = 600 мм.
1	7,80	[(90) 5 /(0) 25 ] s	0,033	1,02
2	7,80	[(90) 4 /(±30) 2 /(0) 22 ] s	0,033	1,01
3	7,80	[45/90/–45/90/45/90/–45/45/(0) 22 ] s	0,034	1,01
4	7,80	[±60/(90) 2 /±60/(0) 22 ] s	0,033	1,00
5	7,80	[±75/90/±75/(0) 22 ] s	0,033	1,02

Укладки неподкрепленной опертой панели при различных базисах

В случае защемления панели по контуру для рассмотренной панели и нагрузок при любом базисе толщина одинаковая, в случае опирания наименьшую толщину дает базис {±45°;90°;0°}. Наибольшая мембранная жесткость получена при базисах {±15°;90°;0°} и {±75°;90°;0°}.

На рисунке 3 для примера приведены собственные формы и фактор потери устойчивости для опертой и защемленной неподкрепленной панели.

Такие же исследования проведены для стрингерной панели. В таблицах 6 и 7 представлены габариты, нагрузки и полученные укладки для стрингерной панели.

На рисунке 4 для примера приведены собственные формы и фактор потери устойчивости для опертой и защемленной стрингерной панели.

Для стрингерной рассмотренной панели и нагрузок при любом базисе толщина одинаковая.

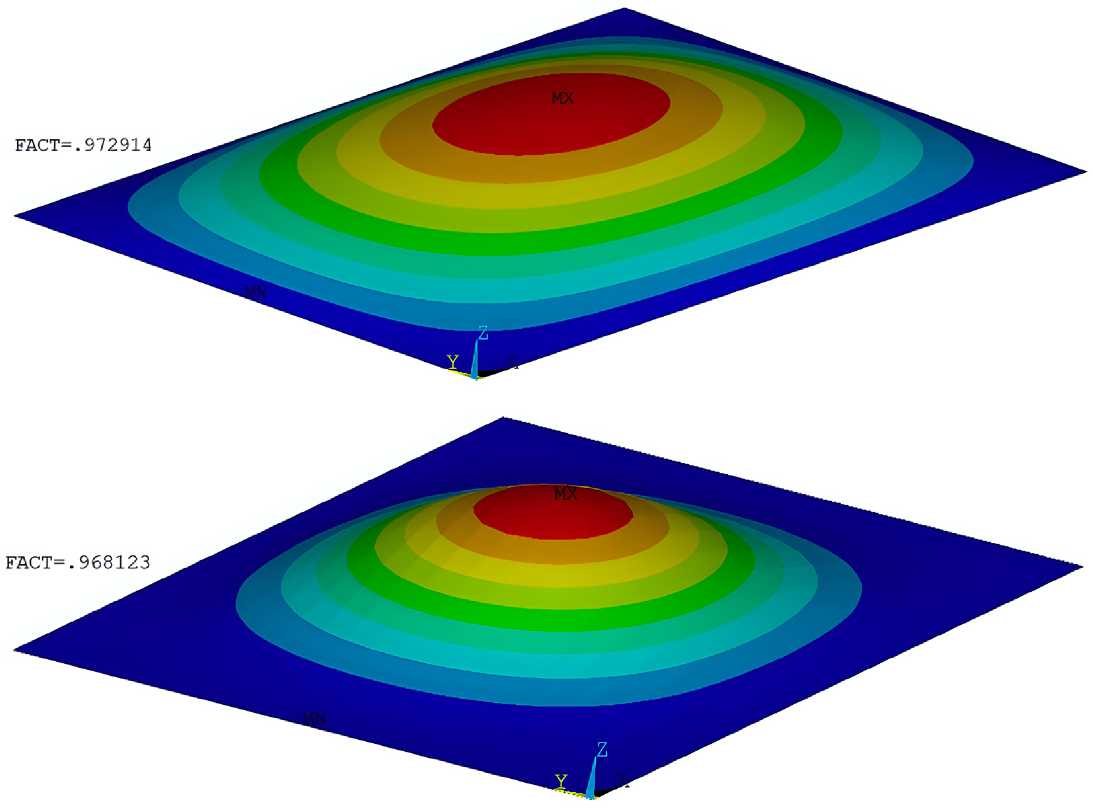
Рисунок 3. Собственные формы и факторы потери устойчивости для неподкрепленных панелей с размерами L = 800 мм, B = 600 мм при нагрузке q1 = –50 кгс, q2 = –10, базис {±60°;90°;0°}: опертая панель (сверху); защемленная панель (снизу)

Таблица 6

№ баз.	h , мм	Укладка	ε i ,%	λ		239
qx = –50 кгс, qy = 0, L = 800 мм, B = 600 мм, hs = 22 мм, ns = 8 мм.
1	6,24	[(±15) 2 /(0) 20 ] s	0,042	1,02
2	6,24	[±30/(0) 22 ] s	0,043	1,02
3	6,24	[45/(0) 23 ] s	0,041	1,02
4	6,24	[60/(0) 23 ] s	0,040	1,01
5	6,24	(0) 48	0,038	1,01
qx = –50 кгс, qy = –10, L = 800 мм, B = 600 мм, hs = 22 мм, ns = 8 мм.
1	7,80	[(90) 2 /(±15) 3 /(0) 22 ] s	0,033	1,01
2	7,80	[±30/90/±30/(0) 25 ] s	0,037	1,02
3	7,80	[±45/90/±45/(0) 25 ] s	0,031	1,02
4	7,80	[(±60) 2 /60/(0) 25 ] s	0,028	1,02
5	7,80	[±75/75/(0) 27 ] s	0,031	1,00

Примечание: q_x – продольный сжимающий поток, q_y – поперечный сжимающий поток, L – длина панели, B – ширина панели, h – толщина панели, h_s – высота стрингеров, n_s – количество стрингеров, λ – фактор потери устойчивости.

Таблица 7

№ баз.	h , мм	Укладка	ε i ,%	λ
qx = –50 кгс, qy = 0, L = 800 мм, B = 600 мм, hs = 22 мм, ns = 8 мм.
1	2,60	[90/15/(0) 8 ] s	0,094	1,11
2	2,34	[30/0/–30/(0) 6 ] s	0,141	1,01
3	2,34	[45/(0) 8 ] s	0,123	1,03
4	2,34	[60/(0) 8 ] s	0,114	1,02
5	2,60	[75/(0) 8 ] s	0,094	1,12
qx = –50 кгс, qy = –10, L = 800 мм, B = 600 мм, hs = 22 мм, ns = 8 мм.
1	3,64	[(90) 4 /±15/(0) 8 ] s	0,064	1,05
2	3,64	[(90) 4 /(0) 10 ] s	0,062	1,05
3	3,64	[(90) 4 /(0) 10 ] s	0,062	1,05
4	3,64	[(90) 4 /(0) 10 ] s	0,062	1,05
5	3,64	[(90) 3 /75/(0) 10 ] s	0,062	1,06

Наибольшую мембранную жесткость дает базис {±75°;90°;0°}.

Заключение

В статье приведены шаги алгоритма выбора рациональных параметров неподкрепленных и стрингерных панелей из слоистого композита. Представлены результаты испытания образцов стрингерных панелей, разработанных с помощью АВРП, на несущую способность при сжатии. Полученное хорошее соответствие предельных нагрузок, определенных в экс ²⁴⁰ перименте и с помощью конечно-элементного анализа, подтверждает эффективность АВРП.

Том 8

Проведенное исследование влияния углов армирования слоев в укладке на толщину и мембранную жесткость панелей показало, что для рассмотренных параметров панелей и сочетаний нагрузок классический базис направлений {±45°;90°;0°} дает наименьшие толщины панелей. При этом в большинстве случаев панели с укладками, содержащими углы ±45°, оказываются и наименее жесткими. Применение базисов с углами ±15° и ±75° не эффективно с точки зрения толщины, однако если есть ограничение по мембранной жесткости, использование этих углов может дать преимущество до 70 %.