Влияние упрочнения на характеристики упругопластического контакта микронеровностей поверхностей

Традиционно [1] фактическая площадь контакта оценивается коэффициентом упругой осадки выступов а , определяемой как отношение фактической площади контакта сферического индентора к площади контакта воображаемой проекции сферы на глубине фактического внедрения индентора. При упругом контакте a =0,5, а при идеально-пластическом а =1,0. Соответственно в идеализированных условиях закономерности изменения а ограничены этими значениями [3]. Однако при выпучивании значения а могут быть больше 1. Уточнить имеющиеся данные можно численными исследованиями упругопластических контактных деформаций с использованием метода конечных элементов (МКЭ), применяя расчётную модель (РМ), описанную в [4]. Исследование с помощью МКЭ подтвердило выпучивание материала полупространства вокруг индентора при его внедрении.

Для анализа влияния выпучивания на коэффициент упругой осадки а были численно исследованы металлы и сплавы, деформируемые идеально-жёстким сферическим индентором. Результаты расчётов МКЭ приведены на рис. 1. Как видно из представленных данных а может быть больше 1 и является функцией не только k ₂= NN _ф2, где к₂ - относительная нагрузка 2-го рода, N_KP 2 - критическая нагрузка 2-го рода, N -текущая нагрузка [4], но зависит от параметров диаграмм напряжённо-деформированного состояния материалов. Полученные результаты удовлетворительно описываются степенной функцией вида

а = А • kn ,

где A и n - коэффициенты, зависящие от параметров диаграмм напряжённо-деформированного состояния материалов.

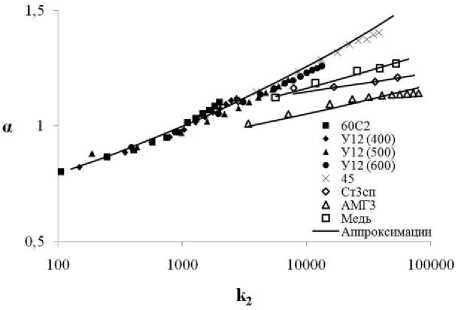
Рис. 1. Влияние выпучивания на изменение коэффициента α от относительной нагрузки k 2

будет после преобразований совпадать с решением, приведённым в работе [3].

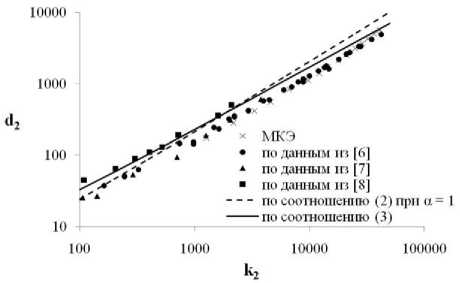
Рис. 2. Сопоставление результатов экспериментальных исследований внедрения сферического индентора с расчётами

Соотношение для расчётов внедрения идеально-жёсткого сферического индентора в упругопластическое полупространство, полученное в работе [3], используя метод относительных нагрузок [5], c учётом выпучивания можно представить в виде:

d 2 = 0 , 2 ■

— + 4 ■ k 2 ■ aVa           7

где d 2 = a / a кр2 – относительное внедрение сферического индентора 2-го рода, а кр2 – внедрение сферического индентора, рассчитываемое по формуле Герца при критической нагрузке 2-го рода.

Учитывая соотношение (1), соотношение (2) можно записать в виде:

Результаты расчётов с помощью МКЭ лучше соответствуют экспериментальным данным, чем расчёты по соотношению (3). Это связано с учётом в РМ не только выпучивания, но и упрочнения металла в процессе деформации. При внедрении сферического индентора упрочнение материала можно учесть эмпирическим законом Мейера [9]. Для нормальной нагрузки N закон Мейера можно записать:

N = G ■(Ip) m,          (5)

d ₂

1 ---------■ 5 А

к 1 - ⁿ

k

V

3      n + 1 '

+ 4 ■ A 2 ■ k₂^T

Для радиуса пятна контакта сферической модели единичной неровности, взаимодействующей с упругопластическим полупространством, на основании геометрических построений и исходя из определения коэффициента α с учётом (3) после преобразований получим:

^ s • R P 2 = ¹ ’⁶ ^ ~

E *

3     3 n + 1 A

■ k 2 + 4 ■ A ² ■ k 2 ²

V                   7

,     (4)

,

где ρ 2 – радиус пятна контакта при использовании относительной нагрузки 2-го рода, R – радиус сферического индентора, σ s – предел текучести, E * - приведённый модуль упругости.

Результаты расчётов по соотношению (3) в сопоставлении с экспериментальными данными, представленными в работах [6-8], а также расчётами, проведёнными МКЭ для аналогичных условий, показаны на рис. 2. Тут же приведены данные для α = 1, при которых соотношение (2)

где G и m - параметры закона Мейера.

а)

б)

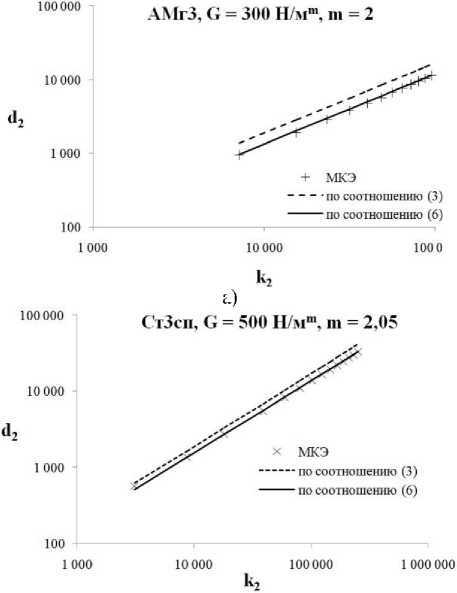
Рис. 3. Влияние упрочнения металлов на характеристики контакта: а) для АМг3; б) для Ст3сп

Учитывая (4) и (5), после преобразований получим:

d ₂

2- mn              2

k₂ m ( 22 • a_s ) m ----------------------• --------------------- •

51 , 5 • A ( G )

2 m - 4

f T7 >----- ■

V ^as R )

Соотношение (6) учитывает как выпучивание материала (коэффициенты A и n ), так и его упрочнение согласно закону Мейера (коэффициенты G , m ). На рис. 3а представлено сопоставление расчётов по соотношениям (3), (6) и с помощью МКЭ для сплава АМг3, а на рис.3б – для мягкой стали. Результаты расчётов по соотношению (6) показывают хорошее совпадение с расчётами МКЭ при указанных значениях параметров G и m .

Выводы: учёт выпучивания и упрочнения может существенно повысить точность расчётов характеристик контакта в условиях упругопластических деформаций. Приведенные данные подчёркивают влияние индивидуальных физикомеханических свойств реальных материалов на особенности формирования контактных упругопластических деформаций. Уточнённые характеристики контактного взаимодействия модели единичной неровности можно распространять на множественный контакт шероховатых поверхностей.