Влияние величины угла раскрыва на фокусирующую способность микроаксикона

онного аксикона в приближении тонкого оптического элемента.

В данной работе рассматривался рефракционный микроаксикон, который может быть изготовлен, например, выращиванием в резисте. Для получения острой фокусировки было предложено использовать линейно-поляризованный лазерный пучок с вихревой фазовой зависимостью. Пучки такого вида можно получить с помощью вихревой фазовой пластинки, в отличие от радиально-поляризованных пучков, которые формируются сложной оптической схемой [13].

Численное моделирование осуществлялось с помощью разностного метода решения уравнений Максвелла (FDTD) [14]. Авторами была получена зависимость размеров фокального пятна от угла раскрыва микроаксикона для Гауссова пучка, а также для лазерного пучка с вихревой структурой фазы.

1. ФОКУСИРОВКА ГАУССОВА ПУЧКА

Рассмотрим конический микроаксикон (рис. 1) с показателем преломления n — 1.5 радиусом R _— 3 мкм в основании, размещенный в свободном пространстве.

При распространении лазерного пучка от основания к вершине за счёт внутреннего отражения от стенок аксикона происходит концентрация излучения возле оси симметрии элемента. Таким образом на острие аксикона происходит фокусировка введённого излучения.

Для моделирования процесса использовался пакет FullWAVE RSoft, реализующий разностное решение уравнений Максвелла в пространственно-временной области (FDTD – метод). Дискретизация по пространственным переменным выполнялась с шагом Л] 20 , по времени -

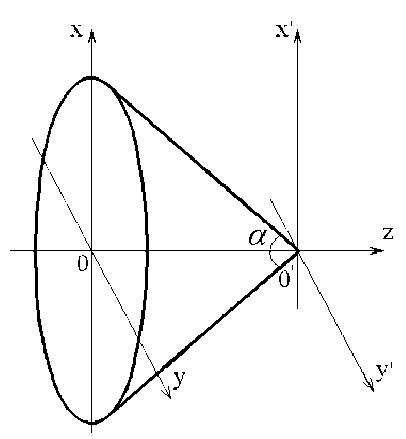
Рис. 1. Микроаксикон в Декартовой системе координат

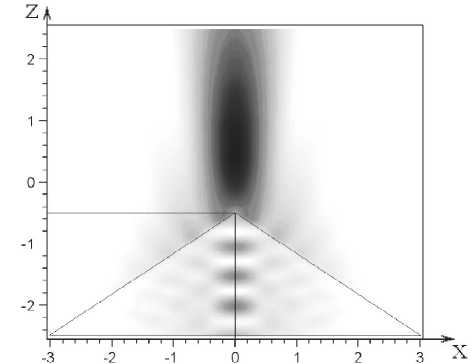
Рис. 2. Интенсивность излучения (негатив) в продольном сечении аксикона

X ( 100 с ) , где X = 1 мкм - длина волны лазерного излучения, с – скорость света.

Для оценки фокусирующих свойств аксико-на с различным углом раскрыва рассмотрим фокусировку гауссового пучка аксиконами с различными углами раскрыва. В качестве начального распределения электрического поля берется линейно-поляризованная вдоль оси x фундаментальная мода Гаусса (1):

E x ( r , Ф ,

z = 0, t = 0 ) = A exp

( r2 )

"

к ° 7

где ( r , фф — полярные координаты в плоскости z = 0, t = 0 (непосредственно в плоскости основания аксикона); A – нормирующий множитель; ° = 1.5 мкм - радиус перетяжки гауссовского пучка.

На рис. 2 приведено распределение интен-

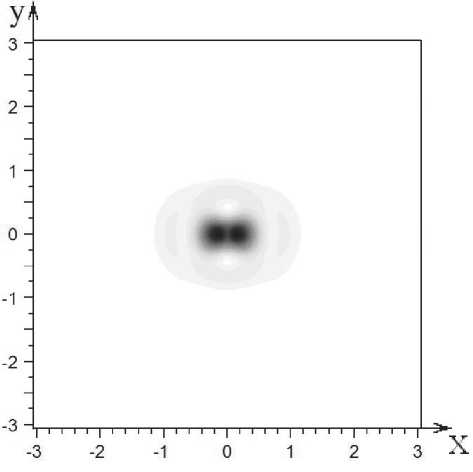
Рис. 3. Интенсивность излучения (негатив) на выходе из аксикона

сивности излучения в продольном сечении ак-сикона с высотой 2 мкм (угол раскрыва равен 112,62 ° ).

На рис. 3 приведено распределение интенсивности в фокальном пятне, полученном при фокусировке моды Гаусса (1) микроаксиконом с углом раскрыва в 88,12 ° .

На рис. 3 видно, что фокальное пятно вытягивается вдоль оси x (оси поляризации), и разделяется на две части. В центре фокального пятна наблюдается провал интенсивности. Это связано с возрастанием z-компоненты колебаний напряженности электрического поля на краях фокального пятна.

Покажем в табл. 1 зависимость ширины фокального пятна FWHM от угла раскрыва аксико-на. Диаметр основания аксикона равен 6 мкм. Также в табл. 1 приведена числовая апертура ак-сикона NA , рассчитанная по формуле (2) [15]:

NA =

1 + ( h(R ) 2

Известно [15], что числовая апертура рассматриваемого аксикона не может превосходить числа 0,75. Максимальное значение числовой апертуры достигается при угле раскрыва акси-кона в 96,38 ° . Если угол раскрыва аксикона меньше, чем 96,38 ° , то будет иметь место полное внутреннее отражение входных лучей от боковых стенок аксикона. Согласно дифракционной теории распространения света, после полного внутреннего отражения из боковой стенки аксикона будут выходить только затухающие волны. Для углов раскрыва, меньших 96,38 ° , числовая апертура теряет свой изначальный физический смысл и является комплексным числом.

Таблица 1. Зависимость интенсивности в центре фокального пятна, а также размеров пятна от угла раскрыва аксикона при фокусировке моды Гаусса (1)

Высота аксикона h, мкм	Угол раскрыва а , градусы	Числовая апертура NA	Интенсивность в центре I, условные единицы	FWHMx, мкм	FWHMy, мкм
2	112,62	0,385	865	0,857	0,627
2,2	107,49	0,442	954	0,772	0,605
2,3	105,05	0,476	982	0,762	0,598
2,4	102,68	0,514	997	0,756	0,591
2,5	100,39	0,56	1005	0,751	0,586
2,6	98,17	0,62	1018	0,764	0,581
2,7	96,03	0,746-0,056 i	1065	0,784	0,043
2,8	93,95	0,748-0,149 i	1084	0,77	0,043
2,9	91,94	0,749-0,2 i	1084	0,765	0,426
3	90	0,75-0,25 i	1126	0,766	0,42
3,1	88,12	0,749-0,29 i	1175	0,76	0,422
3,2	86,30	0,748-0,324 i	1145	0,74	0,4
3,3	84,54	0,747-0,356 i	1102	0,742	0,415

Из табл. 1 видно, что максимальная интенсивность в фокальном пятне достигается при угле раскрыва аксикона, равном 88,12 ° . При этом линейный размер фокального пятна вдоль оси поляризации значительно превышает дифракционный предел.

2. ФОКУСИРОВКА ВИХРЕВОГО ЛАЗЕРНОГО ПУЧКА

Рассмотрим фокусировку вихревого пучка вида (3) микроаксиконом.

E x ( r , ф , z = 0, t = 0 ) = Ar exp

V

Г , X

-2 exp ( i ^ ) . (3) ° 7

Именно такой вид пучка выбран исходя из следующих соображений. В фундаментальную Гауссову моду легко внести фазовую зависимость exp ( гф" ) с помощью вихревой фазовой пластинки. При этом получим начальное распре-

деление exp

V

r

у ²

exp ( i ф ) , у которого

в точке

сингулярности фазы имеется ненулевая амплитуда, что не только затрудняет вычисления, но и невозможно с точки зрения физики. Умножение на радиус пучка, r , обнуляет амплитуду в точке сингулярности фазы. На практике обнуление области сингулярности можно выполнить блокировкой излучения в центральной части.

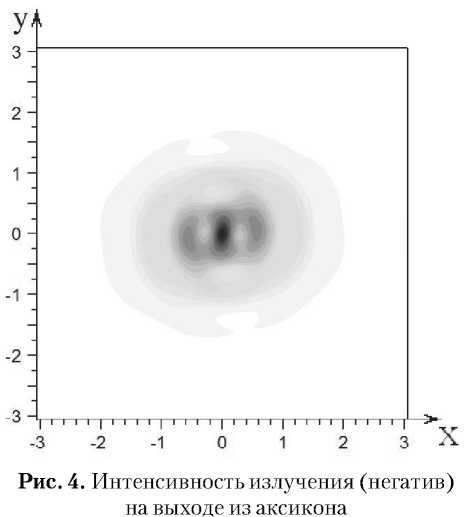
На рис. 4 приведено распределение интенсивности в фокальном пятне, полученном при фокусировке вихревого пучка (2) микроаксико-ном с углом раскрыва в 93,95 ° .

На рис. 4 видно, что фокальное пятно имеет самую высокую интенсивность в середине. Тем

не менее, достаточно сильно выражены боковые лепестки. Это связано с тем, что z-компонента колебаний напряженности электрического поля сфокусирована в центре пятна. А более слабая х-компонента распределена по периферии фокального пятна.

На рис. 5 приведены графики интенсивности электрического поля в сечении фокальных пятен, которые получаются при фокусировке вихревого пучка аксиконом с различными углами раскрыва. По графикам, подобным представленным на рис. 5, рассчитывались линейные размеры фокальных пятен FWHMx.

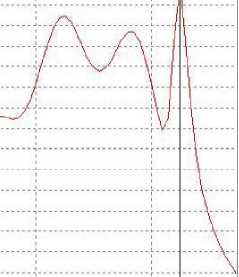
На рис. 6 показано, что фокальное пятно формируется сразу на выходе из аксикона.

На рис. 6 видно, что на выходе из аксикона формируется максимум интенсивности. На ос-

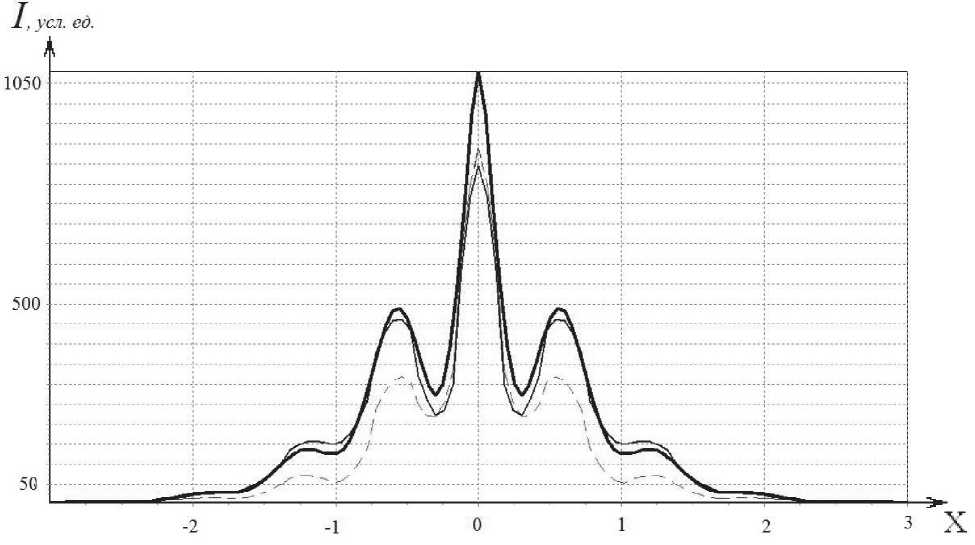
Рис. 5. График интенсивности излучения в центральном сечении фокального пятна для различных углов раскрыва:

толстая линия - угол раскрыва равен 93,95 ° ; линия средней толщины - угол раскрыва равен 86,30 ° , тонкая пунктирная линия - угол раскрыва равен 100,39 °

уел. ед.

ВЫВОДЫ

900850800 750700 650600 550 МО 450 400 360 300 250 200 ISO; 100 50-

Рис. 6. График интенсивности излучения вдоль оптической оси аксикона (оси z).

Две вертикальные черты означают основание (слева) и вершину (справа) аксикона новании этого можно сделать вывод, что фокальное пятно расположено сразу после выхода из аксикона, возле вершины.

Покажем в табл. 2 зависимость ширины фокального пятна FWHM от высоты аксикона. Как и в первом случае, диаметр основания аксикона равен 6 мкм.

Из табл. 2 видно, что максимальная интенсивность в фокальном пятне достигается при угле раскрыва, равном 93,95 °

• 1.    В работе проведено моделирование фокусировки линейно-поляризованного излучения рефракционным микроаксиконом с помощью разностного метода решения уравнений Максвелла.

• 2.    Определены оптимальные углы раскрыва аксикона, при которых фокусировка Гауссова пучка (1) и вихревого пучка (2) является наиострейшей. Для Гауссова пучка – оптимальный угол раскрыва равен 88,12 ° (размер фокального пятна: FWHMx = 0,76 мкм , FWHMx = 0,42 мкм ), для вихревого пучка (2) - 93,95 ° (размер фокального пятна: FWHMx = 0,3 мкм , FWHMx = 0,645 мкм ).

• 3.    Таким образом, в работе была показана возможность формирования компактного фокального пятна с помощью конического микроакси-кона при линейной поляризации освещающего пучка. Для этого достаточно внести в пучок вихревую фазовую зависимость и экранировать область сингулярности фазы (центральной части).