Влияние вертикальной структуры березовых насаждений на распространенность Inonotus obliquus (Pers.) Pil

Введение. Сообщения о степени встречаемости Inonotus obliquus (Pers.) Pil. в разнообразных по сложению насаждениях уже давно не относят к категории библиографической редкости. Следует хотя бы вспомнить довольно красноречивые работы охвата начала, середины и конца предшествующего столетия: Н.И. Катаевской (1928), А.С. Бондарцева (1953, 1959), Т.Л. Николаевой (1961), И.А. Алексеева (1970), Ю.В. Синадского (1962, 1973), Г.И. Конева (1968), Э.И. Слепяна (1961), А.М. Жукова (1978), А.Т. Вакина (1969, 1952, 1955), М.А. Бондарцевой (1986), Э.Х. Пармасто (1986), Н.А. Черемисинова (1970), В.А. Суркова (1998), М.Е. Павловой (1998), а за рубежом В.А. Кампвеля и Р.В. Давидсона (1956), Л. Харочи и З. Игманди (1953) и других, которые также и установили, что стерильная форма факультативного сапротрофа представляет собой плотное сплетение мицелия Poria obliqua Quel (= Xantochrous obliquus Pers B. et G. = I. obliquus (Pers) Pil) с хаотичной, беспорядочной, конкатенацией однородных (гомогенных) грибных нитей без дифференциации на ткани [17–23, 28, 34–36, 38]. Продолжают постепенно набираться сведения о природе скошенного трутовика и в XXI веке, что определенно свидетельствует о пока еще далеко незавершенном характере исследований в этой области и требующих привнесения очередного коррегирования. К этому периоду времени принадлежат труды ряда ученых – Т. Ниемеля (2001); В.А. Власенко (2010); Н.А. Галынская и И.М. Га-ранович (2009); Е.А. Арковенко (2007); С.В. Волобуев и С.Ю. Волкова (2008); С.П. Арефьев (2000-2005, 2010); Y.-C. Dai (2010); B.-K. Cue, P. Du, Y.-C. Dai (2011); J. Schumacher, P. Heydeck, A. Roloff (2001); И.А. Горбунова и др. (2009); С.М. Музыка (2009); Н.И. Гаврицкова и Т.Х. Гордеева (2011); Т.Н. Барсукова, О.В. Мамедова (2001) и прочих [2–16, 24–27, 31–33, 40–42]. В означенных материалах авторами приводится обширный спектр и оценка степени варьирования распространенности рассматриваемого патогена в лесах различных формаций, как по уровню и градиентам факторов, так и собственной численности. Например, Г.И. Конев (1968) отмечает большие запасы чаги в таежной зоне Западной и Восточной Сибири, в древостоях с доминированием березы, а также в пихтово-кедрово-еловых лесах с березовой примесью. Л. Харочи и З. Игманди (1957) указывается, что в одном из искусственно заложенных насаждений ясеня высокого (с. Икервар) контагиозность вследствие I. obliquus составляла порядка 20–25%, а количество экземпляров дуба чернильного, пораженного базидиомицетом, в гослехозе г. Дьер достигало 44,4%, причем более чем на 10% стволов наблюдалось свыше двух наростов (клубеньковых тела). По сообщению З. Игманди (1953), потеря деловой древесины от гриба X. obliquus B. et G. может доходить до 10% и более [Цит. по: 34]. J. Schumacher, P. Heydeck и A. Roloff также охарактеризовали довольно частым распределение Inonotus obliquus в синузиях ольхи черной, или клейкой (Alnus glutinosa (L.) Gaertn.), формирующей национальный парк Передней Померании в Германии [42]. Хотя при обследовании лесопосадок Щелковского учебно-опытного лесхоза Московской области Ю.В. Синадским (1962) была отмечена лишь единичная зараженность берез чагой [34].

Неоднозначным продолжает оставаться и вопрос относительно дефиниций влияния факторов самой различной природы на появление скошенного трутовика в насаждениях. Уместно напомнить, что в подавляющем большинстве случаев авторы (не только представленные выше) исследуют определенную их (групп факторов) компоненту, упуская из внимания всю сложность взаимодействия совместных интеграций, антагонизма – во-первых, а, во-вторых, объектом их изучения все чаще выступает не обособленный организм, а микобиотный комплекс, что сильно затрудняет установление однозначных адекватных статистических (а иногда и функциональных) зависимостей между показателями.

Распределение растительности по вертикали, будь то: биогеоценоза, консорции, насаждения и т.д., т.е. их форма, является одним из главных таксационных признаков и неотъемлемой, внутренне присущей, или, иначе, имманентной, характеристикой почти любой флористической системы (прежде всего дендрологической), поскольку от него (нее) зависит не только проведение многих лесохозяйственных мероприятий в дальнейшем – адвентивное следствие, но и непосредственно ход роста, биоэкология пород. Тем становятся актуальнее экспериментальные модели, полностью или частично вбирающие в себя либо коллатерально затрагивающие этот аспект структуры фитосоциальных отношений (по выражению Стороженко В.Г.), учитывающие посредством детального анализа вертикальных проекций растительного продуцентного континуума направление хозяйственной деятельности. Последнее и сподвигло автора настоящей статьи обозначить данный эмпирический опыт, цель которого изучить влияние формы березовых древостоев на диффузную структуру сапрофильного базидиального макромицета Inonotus obliquus .

Объекты и методы исследования. С целью выявления влияния формы березовых насаждений на диссеминацию (дисперсию) гриба были рассмотрены древостои, имеющие как простую (однопологовую), так и сложную (двухпологовую) структуру. Поскольку подлесок из липы по различию средних таксационных признаков с пологом березы в большинстве случаев не отвечал условиям выделения из него второго самостоятельного яруса, а также и то, что межвидовые взаимоотношения деревьев, происходящие внутри консорт-ных растительных сообществ, заходят далеко за рамки обозначенной проблемы и удостоены наиболее пристального внимания во многих фундаментальных работах как отечественных, так и зарубежных авторов, названная порода не ассоциировалась со вторым отдельным ярусом. Второй же полог был репрезентирован более молодой генерацией (поколением) березы. Параметры таксации подбирались таким образом, чтобы находило свое тождество соответствие насаждений структуре региона, а само разделение леса на ярусы не противоречило бы требованиям Лесоустроительной инструкции 2008 г. [29]. Эмпирическая кратность составляла 7. Каждая проба представляла собой безразмерную учетную площадь с разрешением в 1000 экземпляров деревьев. Подрост учитывался как новое поколение леса [37], а не как самодостаточный древесный ярус. Третий ярус древостоя не выделялся; он фактически отсутствует не только в Ульяновском регионе, но и на территории всей России [1]. Наиболее часто встречались насаждения с одноярусной стратегией, реже двухъярусной. Береза и все светолюбивые таксономические виды, как правило, растут в виде простых древостоев. Однако при изреживании полога к ним иногда подселяются теневыносливые породы, которые в принципе допускают и организацию второго яруса. В насаждении, состоящем из деревьев одной породы, может образоваться несколько фитоценотических горизонтов по возрастным поколениям. При этом в верхнем сечении биогеоценоза будут располагаться деревья старшего возраста, а во втором и всех последующих – более молодые. Все это необходимо принимать во внимание при экстраполяции результатов на сегменты, мозаики и парцеллы растительности больших территорий.

Статистическая проработка эмпирических данных осуществлялась способом бинарных сопоставлений, допускающим проведение математического анализа сравниваемых выборок по параметрам нормального распределения Гаусса или распределения Стьюдента [39].

Дисперсионный анализ производился методом однофакторных ортогональных комплексов. В роле фактора F выступала таксационная форма количественного результата X и, соответственно, отклика – агре-гированности базидиального ксилосапротрофа I. obliquus. Матрица наблюдений (или иначе комбинационная табличная сетка) частично отображена ниже в таблице 1. Как из нее следует, число градаций фактора сло- жено двумя гетерогенными типами. Количество (численность) константных уровней обозначим через p, следовательно, сами уровни будут выглядеть как F1, F2 , …, Fp . Проведенные испытания на каждой градации организованного (регулируемого) фактора – q (в нашем случае по 7 конкордантных вариант). Результаты наблюдений – числа xij , где i – номер испытания (i = 1, 2, …, q), j – номер уровня фактора (j = 1, 2, …, p).

Определим задачу: на уровне значимости а проверить нулевую гипотезу о равенстве средних совокупностей при допущении, что групповые генеральные дисперсии хоть и неизвестны, но подобны. Для ее решения введем: интегральную сумму квадратов отклонений наблюдаемых значений признака от кумулятивной средней арифметической pq

EE ( X j - x ) 2 ;

j = 1 i = 1

факторную сумму квадратов колебаний кластерных средних от общего математического ожидания (характеризует рассеяние «между группами»)

^Sфакт = q E ⁽ x rpj — x ^{) 2} ;

j = 1

остаточную сумму квадратов флуктуаций наблюдаемых значений группы от своей групповой средней (дефинирует рассеяние «внутри групп»)

q                 ₂ q                  ₂             q                  ₂

ост / j X 11      гр 1/     / j \ 12      гр 2/     "’    / j X p      PPP / i=1                               i=1                                           i=1

Практически остаточная производная сумма находится по упрощенному равенству

S

ост

общ

—

S

факт .

Однако для вычисления общей и факторной сумм все же более удобны следующие аналитические формулы:

S общ

2 pp =XPj-ER  /(pq), j=1       L j=1 J /

S

факт

= E Rjq ^- E Ri /( pq ) , j= 1            L j = 1 J /

q где  Pi = Ex, — сумма квадратов наблюдаемых значений признака на уровне Fj;

i = 1

q

R j = E x _ij — сумма наблюдаемых значений признака на уровне F j .

i = 1

Разделив уже вычисленные факторную и остаточную суммы (девиаты) на соответствующее число степеней свободы, найдем факторную и остаточную дисперсии:

2       S факт    2

s факт          i , s ост p - 1

S ост

.

—

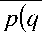
Наконец, сравним факторную и остаточную дисперсии по критерию Фишера-Снедекора s2

.

факт

^Рф = .2

s ост

Изначально предположим (классическая H ₀ -гипотеза), что генеральные межгрупповые средние и дисперсии равны между собой и различия, наблюдаемые между выборочными показателями, вызваны случайными стохастическими причинами, а не влиянием на признак регулируемых факторов (или единственного фактора как здесь). Нулевая гипотеза отвергается и эффективность действия фактора F на результативный признак X признается статистически аутентичной, если Р ф >  F st . В противном случае принимать альтернативную (конкурирующую) гипотезу нельзя.

Число степеней свободы вычисляли по формулам k 1 = p -1, k 2 = p (q -1).

Для количественной оценки дескрипции употреблялись коэффициенты детерминации [30]:

S кДфакт = ф -100. k дот = S' '100.

общ                    факт

Результаты и их обсуждение. В таблицу занесены данные по распространенности I. obliquus в березовых древостоях, имеющих одно- и многоярусную структуру.