Влияние вида кинетических функций на закономерности превращения в тонком слое, расположенном на подложке, в условиях управления подвижным источником тепла

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2024PNRPU MECHANICS BULLETIN

При получении новых материалов в современных технологиях важную роль играют физико-химические превращения, следствием которых и являются новые состав, структура и свойства [1; 2]. Особое внимание в последние десятилетия уделяется процессам, которые происходят в твердом состоянии. Это объясняется тем, что в некоторых случаях именно твердофазные реакции являются наиболее эффективным способом для получения новых веществ и материалов. В некоторых случаях только процессы в твердом состоянии могут преобразовать вещество в форму, которая отвечает заданным требованиям, то есть позволяют создать материал с необходимыми свойствами, к примеру, изготовить кристаллы с определенной концентрацией нужных дефектов [3]. К современным и развивающимся классическим технологиям, в которых важную роль играют химические реакции, можно отнести спекание в твердой и жидкой фазах [4], управляемый синтез покрытий [5], синтез композитов [6], создание материалов и изделий в 3D-технологиях [7; 8] и др.

В твердых телах механизмы и динамика физикохимических процессов отличаются от тех, которые наблюдаются в жидкостях или газах [2; 9], в частности, из-за значительно меньшей скорости диффузии, которая в твердых материалах на порядки ниже [10]. Это замедление приводит к тому, что концентрация веществ в системе не успевает выравниваться, что вызывает про- странственную локализацию протекающих процессов [2; 11]. Локализация процессов влияет на кинетику реакции, где важную роль играют как удельная скорость процесса (или коэффициент диффузии), так и геометрия реакционной области. Эти характеристики, зависящие от геометрии, называются топохимическими [12; 13]. Кроме того, поскольку реакции происходят в определенных пространственных зонах, их скорость может зависеть как от процессов на границе раздела фаз (реакционный контроль), так и от скорости переноса реагентов к этой границе или удаления продуктов реакции (диффузионный контроль) [9; 11]. Любая твердофазная реакция совершается в виде существенно большего набора промежуточных состояний (которые энергетически мало отличаются друг от друга, по сравнению с реакциями в газовой и жидкой фазах) [14]. В простых системах, к которым применимы определенные модельные предположения, можно экспериментально выявить эти режимы по характеру зависимости степени превращения от времени.

Первые попытки разработать достоверные модели кинетики твердого тела относятся к концу 1920-х гг. (G. Tamman, G. Yander, S. Roginsky и др.). Дальнейшие исследования привели к разработке более полных кинетических моделей [15], учитывающих различные механизмы реакции на микроуровне [16 – 19].

В кинетике химических реакций в твердых телах потеря массы твердого вещества-реагента выражается в так называемой степени превращения ( Y ), которая изменяется в диапазоне от 0 до 1 и определяется как [18]

Y = m 0 - m t m о - m „ ,

где m 0 – начальный вес образца, m t – вес образца в момент времени t , а m ∞ – конечный вес образца. Однако если вес образца в ходе реакции не изменяется, степень превращения можно ввести иным способом. Положим, M_A и M_P – текущие массы реагентов и продуктов реакции, так что

M A + M P = M = const

и

M A + M P. = C + C = 1.

MM AP

Величину

Y = Cp = 1 — CA тоже можем назвать степенью превращения или долей продукта реакции.

Заметим, что подобное понятие можно ввести и в рамках термодинамики необратимых процессов [20]. Для простой реакции вида vAA ^vpP                (2)

ее скорость Ф может быть выражена через изменение числа частиц любого сорта – реагентов n_A или продуктов n :

B ф = 1 dnA = 1 dnP = d ^ = dY v A dt v P dt dt dt ’ где ^ = Y - координата реакции, степень полноты реакции или степень превращения; vA и vB - стехиометрические коэффициенты.

Скорость твердофазной реакции Ф в химии твердого тела представляет собой изменение во времени степени превращения вещества и пропорциональна произведению константы скорости k(T) на дифференциальную скорость реакции φ (Y):

dY ₌^ф = k ( T ) ф ( Y ) .

Константа скорости обычно подчиняется закону Аррениуса постоянная. То есть, в неизотермических условиях это уже не константа, а функция температуры.

Дифференциальная скорость реакции – кинетическая функция – φ( Y ) является функцией степени превращения, и ее форма зависит от основного механизма твердофазной реакции на микроуровне. Полноправными стадиями реакций с участием твердых веществ являются зарождение и рост малой доли продукта в местах несовершенств (нуклеация); диффузия, механизмы которой могут быть разнообразными (объемная и поверхностная, по границам зерен и фаз, по механизмам внедрения и замещения) и зависят от наличия дефектов; геометрические особенности, приводящие к преимущественному росту продукта в разных направлениях, и т.д. [12; 13].

Интегрируя уравнение (2) при T = const по времени, можно получить так называемую интегральную форму скорости реакции g ( Y ):

g ( Y )

k < ^Л >            Л

Г 1 dY           - E t

Ы ~d= ^k = ^k o e^xP⁽^7) I ^dt ^ g ⁽ Y ) = ^kt ■   ⁽⁵⁾

о ^ ( Y ) at              RT о

В табл. 1 приведены наиболее часто используемые модели, учитывающие различные механизмы реакции. Первый столбец таблицы включает названия моделей.

Все используемые здесь модели делятся на четыре семейства, a именно: модели зарождения, геометрического сжатия, диффузии и модели порядка реакции. Таким образом, в таблице мы можем найти каждое семейство (выделено курсивом) и под ними соответствующие модели. Названия моделей, приведенные в таблице, представлены в виде буквы, присоединенной к целому числу (например A2). Буква отражает тип модели, a целое число связано с механизмом реакции, рассматриваемым в каждом конкретном случае.

B частности, символы P, A, R, D, F означают закон мощности, закон Аврами – Ерофеева, изменение объема смеси, диффузию и реакцию-порядок соответственно. Подробные сведения обо всех используемых здесь моделях, механизмах реакций и выводах каждой модели, представленных в таблице, можно найти в литературе [12; 13; 21–25]. Кроме того, на втором и третьем столбце таблицы приведены формы так называемых дифференциальных и интегральных скоростей реакций соответственно для различных моделей.

В [26] предложено обобщенное уравнение, которое в наших переменных имеет вид k (T ) = kо exP ^- E^ ,

dY = k [(1 — Y) q ]'{[1 — (1 — Y)‘-q ] /(1 — q )}Y •

где k0 – предэкспонент, Е – энергия активации химической реакции, φ – кинетическая функция, R – газовая где q, β и γ – характеристические параметры для каждого конкретного механизма реакции.

Таблица 1

Набор различных моделей твердофазных реакций и их скорости, представленные в дифференциальной и интегральной формах

Set of different models of solid-phase reactions and their rates represented in differential and integral forms

Table 1

Модели	1 dY Дифференциальная форма ф ( Y ) = kdt	Интегральная форма g ( Y ) = kt
Модели нуклеации
Степенной закон (P2)	2 Y 1/2	Y 1/2
Степенной закон (P3)	3 Y 2/3	Y 1/3
Степенной закон (P4)	4 Y 3/4	Y 1/4
Аварами – Ерофеева (A2)	2(1 – Y )[- ln(1 – Y )]1/2	[- ln(1 – Y )]1/2
Аварами – Ерофеева (A3)	3(1 – Y )[- ln(1 – Y )]2/3	[- ln(1 – Y )]1/3
Аварами – Ерофеева (A4)	4(1 – Y )[- ln(1 – Y )]3/4	[- ln(1 – Y )]1/4
Проут – Томпкинса (B1)	Y (1 – Y )	ln[ Y /(1 – Y )]+cY
Модели геометрического сужения
Сокращающаяся область(R2)	2(1 – Y )1/2	1-(1 – Y )1/2
Сокращающийся объем(R3)	3(1 – Y )2/3	1-(1 – Y )1/3
Модели диффузии
1-D диффузия (D1)	1/(2 Y )	Y 2
2-D диффузия (D2)	-[1/ ln(1 – Y )]	((1 – Y )ln(1 – Y ))+ Y
3-D диффузия-Яндера (D3)	[3(1 – Y )2/3]/[2(1-(1 – Y )1/3)]	(1-(1 – Y )1/3)2
Гистлинга – Браунштейна(D4)	3/[2((1 – Y )-1/3-1)]	1-(2/3) Y -(1 – Y )2/3
Модели порядка реакции
Нулевого порядка(F0/R1)	1	Y
Первого порядка (F1)	(1 – Y )	-ln(1 – Y )
Второго порядка (F2)	(1 – Y )2	[1/(1 – Y )]-1
Третьего порядка (F3)	(1 – Y )3	(1/2)[(1 – Y )-2-1]

В макрокинетике [27; 28] при описании синтеза новых материалов в режиме послойного горения или теплового взрыва, при синтезе в растворах [29] и в условиях экструзии [30] используется подобный подход к описанию кинетики реакций. Однако имеются и более «продвинутые» модели. Например, для учета торможения реакции слоем твердофазного продукта на основе решения специальных задач используются кинетические законы, включающие параметры торможения [31, 32]. Так, если продукт реакции и реагенты (или хотя бы один из реагентов) не плавятся, химическое взаимодействие осуществляется путем диффузии реагентов через слой образовавшегося продукта, который разделяет реагенты и препятствует дальнейшему протеканию реакции. Полного смешения реагентов не происходит, и реакция носит существенно гетерогенный характер. Вид кинетической функции в таких системах определяется механизмом переноса реагентов и структурой нарастающего слоя продуктов, что отражает кинетическая функция вида

Ф d ( T , Y ) = e - mY Y - n , (6)

Если механизм реакции нельзя свести к единственной суммарной реакции (2), то можно использовать и классические представления химической кинетики о параллельных, последовательных, конкурирующих реакциях и др. [33]. Например, реакцию, протекающую в две последовательные стадии, можно представить так:

A ^ B ^ P, где B – промежуточный продукт первой реакции и реагент для второй реакции. В этом случае понятия концентрации и степени превращения не тождественны. Систему кинетических уравнений можно записать как относительно концентраций веществ, определенных аналогично предыдущему CA + CB + CP = 1, так и относительно координат первой и второй стадий. Для первого варианта имеем систему кинетических уравнений dС

—B = Ф .

dt

-Ф ₂ = k . ( T ) C a - k 2 ( T ) C b ,

С = Ф2 = k2 (T) Cb , dt где m, n – параметры торможения.

Наиболее распространены следующие законы: m = 0         n = 0 - линейный, m = 0         n = 1 - параболический, m = 0         n = 2 - кубический, m > 0         n = 0 - экспоненциальный.

а C_a = 1 - C_b - C_p .

Заметим, что классический формально-кинетический подход к описанию кинетики реакций, учитывающий параллельные и последовательные стадии, может быть вполне модифицирован за счет учета торможения реакций слоем продукта [34; 35]. Тогда для последова- тельной реакции с неплавящимся конечным продуктом P

Ф 2 ( T , C B , C P ) = k 2 C B e - ^mC P C P - n .

Обзор двухуровневых моделей, в которых явно учитываются особенности диффузионно-контролируемых реакций, представлен в [36]. К сожалению, для большинства твердофазных реакций такой подход пока остается весьма условным.

Цель настоящей работы состоит в исследовании влияния вида кинетического закона на термокинетические закономерности синтеза покрытия на подложке.

подложке и покрытию; x ₀ – начальное положение источника; R ₀ – эффективный радиус луча лазера; V – скорость его движения вдоль оси OX ; f – коэффициент отражения; q ₀ – эффективная плотность мощности источника тепла; T e – температура окружающей среды; σ – постоянная Больцмана; ε – эффективная степень черноты поверхности; T_W – температура объектов (стенок камеры), с которыми идет обмен излучением; a f -эффективный коэффициент теплообмена.

В случае простейшей суммарной реакции типа «реагент – продукт» для описания кинетики требуется одно уравнение вида (3). В этом случае в (7)

Постановка задачи

Математическая модель процесса лазерного синтеза покрытия на подложке [37; 38] в одномерном приближении и без учета сопутствующих синтезу механических процессов включает уравнение теплопроводности, осредненное по толщине пластины с подложкой, и уравнения кинетики, соответствующие выбранной модели. В настоящем исследовании изменение пористости и толщины порошкового слоя, а также зависимость свойств от температуры и состава не учитываются. Одномерная постановка задачи корректна при условии сканирования луча с высокой частотой по всей ширине пластины.

Уравнение теплопроводности имеет вид

U ЭT  ';(W ЭT| + W^ + hBWch - H (T)

d t   Эx V   dx ) hA + hB где

W = Q d-

Замыкают задачу граничные и начальные условия x = 0: W — = aAhA +aBhB (T -Te) + d x     hA + hB

+ ^ e AhA + e BhB hA + hB

;

d T a x ^ ^ : — = 0 ;

dx t = 0: T = T0.

Для описания плавления, если его необходимо учитывать, вводим интервал температур плавления T s – T L и n L — долю жидкой фазы.

В этом интервале доля жидкой фазы изменяется по заданному закону:

W = X A

+x B^hB— ^hA ^{+ h}B      ^hA ^{+ h}B

h

^U = cA P A Ai, ^hA ^{+ h}B

hB

⁺ c B ^P B ^hA ^{+ h}B

n L =

или

n L = 0, T <  T s ,

T - Ts I Tl - Ts)

, T s <  T <  T L

– эффективные теплофизические свойства; (коэффициент теплопроводности и объемная теплоемкость);

1 ( TL - TI nL =1 -l T т I

V T L T s )

, T s <  T <  T L ,

^Wext = q 0 ( 1 - ^f ) ^exP

I x - x 0 - Vt I

Д R о 1,

Тогда

n L = 1, T >  T l .

– источник тепла, соответствующий внешнему нагреву;

H ( T )=a£0 ( T4 - Te4 ) + a eff ( T - Te )        (11)

– потери тепла излучением (первое слагаемое) и конвекцией (второе слагаемое).

Здесь T – температура, t – время; x – пространственная координата: X _k , c_k , p _k - коэффициенты теплопроводности, плотности и теплоёмкости материалов; h_k – толщины слоев; индексы k=А и k=В соответствуют

^CB ^P B = [ ^CB ^P B ] ₀ ^{( 1 n} L ^{) + P} B 0 ^L

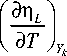
n L , где L – эффективная теплота плавления (Дж/кг).

Для исследования выберем несколько простых вариантов.

В простейшем случае имеем реакцию первого порядка по реагенту ф(Y) = 1 - Y (вариант I), реакцию второго порядка по реагенту ф(Y) = (1 - Y)2 (вариант II), автокаталитическую реакцию ф(Y) = (1 - Y)(Y) + Y) (вариант III) и реакцию, скорость которой тормозится сло- ем твердофазного продукта с экспоненциальным торможением ф(Y = (1 - Y)exp(-SY) (вариант IV).

В качестве примера более сложной ситуации рассмотрим систему последовательно-параллельных стадий, соответствующих синтезу на подложке композита из смеси порошков оксида титана TiO 2 и алюминия Al (вариант V). В предположении, что процесс можно описать двумя суммарными стадиями – образование оксида алюминия с освобождением титана и вступление титана в реакцию с алюминием с образованием интерметалли-да [39; 40]:

3TiO 2 + 4Al = 2Al 2 O 3 + 3Ti и Ti + 3Al = TiAl 3 .

Фактически первая реакция соответствует образованию упрочняющих частиц. Состав матрицы образуют оставшиеся алюминий и титан, а также интерметаллид. В этом случае в каждый момент времени в системе находятся 5 веществ Al , Ti , TiO 2 , Al 2 O 3 , Al 3 T , для массовых концентраций которых вводим обозначения C 1 , C 2 , C 3 , C 4 , C 5 . В упрощенной схеме (12), (13) не учитываются детальные пути реакций. Однако если имеется хотя бы такая формальная запись, то все законы формальной кинетики и термодинамики тоже можно применять [20]. Система кинетических уравнений в данном приближении имеет вид [37]:

dC 1 dt

— (4Ф1 + 3Ф 2); m sum dC2 dt

= m  ( 3 ф 1 -ф 2 ) ;

sum

dC 3 dt

m

= -3—Ф 1 ;

m

sum

C = 2 i ф

dt

m

1 ^;

sum

dC 5 dt

m

= — ^Ф2 '

m sum

Вместо одного из уравнений можем использовать баланс масс.

X с = 1.

к = 1

В (3):

Ф 1 = _Z 10 С 1 ⁴ С 3 exp

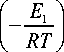
; Ф 2 = z 20 С 1 С 2 exp

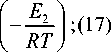
m_k – молярные массы компонентов (кг/моль);

m sum = X m_k ; E 1 и E 2 энергии активации реакций к - 1

(Дж/моль); z 10 и z 20 – предэкспоненциальные факторы (1/с).

Химическое тепловыделение, в отличие от (12), включает 2 слагаемых:

Wch = Qch ,1ф1 + Qch,2Ф 2, где Qch,1 и Qch,2 – тепловые эффекты химических реакций (Дж/м3).

Задача решается численно. Алгоритм численного решения аналогичен [37; 38]. В общем случае модель [37] позволяет исследовать динамику фазообразования при варьировании параметров внешнего источника тепла, потерь тепла. Имеется возможность учета зависимости эффективных свойств от температуры и состава, а также от пористости.

Результаты

В расчетах принято, что подложка – это титан, а верхний слой содержит в своем составе большую долю алюминия. Изменение свойств с температурой и составом не учитываем, так как цель исследования состояла в изучении роли кинетических функций. Однако учитываем, что покрытие – это пористый слой с заданной пористостью θ = θ 0 = 0,3. Тогда

X а = 0,219, X в = 2,37 (1 - 9) Вт/(см - К);

ρ А = 4,54, ρ В = 2,7 (1 – θ) г/см³;

с А = 0,524, с В = 0,903 Дж/К.

Так как для лазерной технологии потери тепла обеспечиваются, в основном, конвекцией, принято:

a eff =10 Дж/(см² - с - К), ё а = е в = е о = 0.

Задано: T 0 = T е =300 К; L S = 5 см (длина заготовки); И а 1, h B = И в 0 =0,1 см; Q m = ( Q m _Al + Q m _Al2O3 )/2 ~ ~ 398 Дж/г; (эффективная теплота плавления); T_S = 933, T L = 2327 K; R 0 = 0,05 см; f = 0,45.

Скорость движения источника тепла вдоль оси OX V = 5 см/с; эффективная плотность мощности источника тепла q ₀ (Дж/(см² - с)), варьировалась.

При протекании единственной химической реакции принято:

Q ch = 3000 Дж/моль; E _ch= 2 - 10 5 Дж/моль; z ₀= 1 - 10 9 1/с.

В варианте с двумя реакциями:

Q ch,1 = 3000 Дж/моль; E ch,1 = 2 - 10 5 Дж/моль;

z 0,1 = 1 - 10⁹1/с;

Q _ch , ₂= 2000 Дж/моль; E _ch , ₂ = 1,8 - 10 5 Дж/моль;

z 0,2 = 5 - 10⁸1/с.

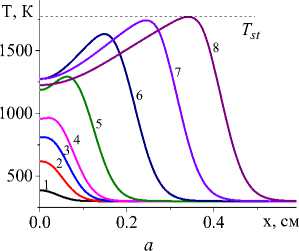
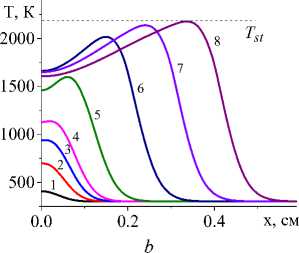
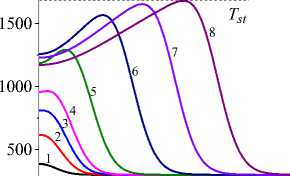
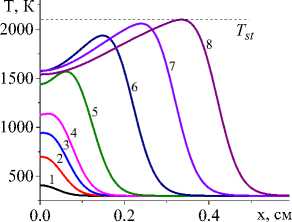
На рис. 1 показана начальная стадия развития процесса до установления квазистационарного режима для единственной реакции и кинетических функций двух видов (варианты I и IV). Очевидно, что чем выше плотность мощности источника тепла, тем выше достигаемая в процессе максимальная температура (рисунки справа и слева). Максимальная температура отмечена пунктирной линией. К моменту времени 0,8 с (кривые 8 ) процесс можно считать установившимся для всех представленных на рисунке вариантов.

Чем выше температура, тем больше доля жидкой фазы (рис. 2). Вид кинетической функции на нее не оказывает влияния. По мере продвижения источника, температура в оставшейся за ним части образца падает, что, очевидно, приводит к уменьшению и доли жидкой фазы. В квазистационарном режиме максимальная доля жидкой фазы также не изменяется. Рисунки представлены для единственной (суммарной) химической реакции и кинетических функций двух видов (варианты I и IV).

T, К

0.0         0.2         0.4 x, см

d

c

Рис. 1. Распределение температуры в последовательные моменты времени: 1) 0,001; 2) 0,004; 3) 0,007; 4) 0,01; 5) 0,02; 6) 0,04;

• 7)    0,06; 8) 0,08 c для вариантов I (рисунки слева) и IV (рисунки справа) при q 0 =4 ⋅ 10⁵ Дж/(см² ⋅ с) и α eff =15 Дж/(см² ⋅ с ⋅ К) ( а и c ); при q 0 =5 ⋅ 10⁵ Дж/(см² ⋅ с) и α eff =10 Дж/(см² ⋅ с ⋅ К) ( b и d )

Fig. 1. Temperature distribution at successive time points: 1) 0.001; 2) 0.004; 3) 0.007; 4) 0.01; 5) 0.02; 6) 0.04; 7) 0.06; 8) 0.08 s for variants I (pictures on the left) and IV (figures on the right) at q 0 =4 ⋅ 10⁵ J/(cm² ⋅ s) and α eff =15 J/(cm² ⋅ s ⋅ К) ( а and c ); at q 0 =5 ⋅ 10⁵ J/(cm² ⋅ s) and α eff =10 J/(cm² ⋅ s ⋅ К) ( b and d )

d

Рис. 2. Распределение доли жидкой фазы в последовательные моменты времени: 1) 0,001; 2) 0,004; 3) 0,007; 4) 0,01; 5) 0,02; 6) 0,04; 7) 0,06; 8) 0,08 с для вариантов I и IV при q 0 =4 ⋅ 10⁵ Дж/(см² ⋅ с) и α eff =15 Дж/(см² ⋅ с ⋅ К) ( а и c ); при q 0 =5 ⋅ 10⁵ Дж/(см² ⋅ с) и α eff =10 Дж/(см² ⋅ с ⋅ К) ( b и d )

Fig. 2. Distribution of the liquid phase fraction at successive moments of time: 1) 0.001; 2) 0.004; 3) 0.007; 4) 0.01; 5) 0.02; 6) 0.04;

• 7)    0.06; 8) 0.08 s for variants I (pictures on the left) and IV (figures on the right) at q 0 =4 ⋅ 10⁵ J/(cm² ⋅ s) and α eff =15 J/(cm² ⋅ s ⋅ К) ( а and c ); at q 0 =5 ⋅ 10⁵ J/(cm² ⋅ s) and α eff =10 J/(cm² ⋅ s ⋅ К) ( b and d )

  

  0.0         0.2         0.4 x, см

  
  
  
  
  
  
  
  
  
  
  

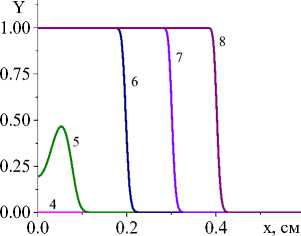
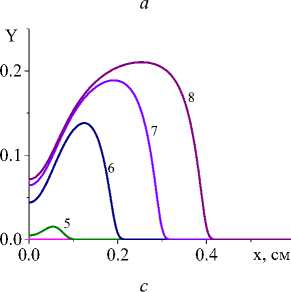
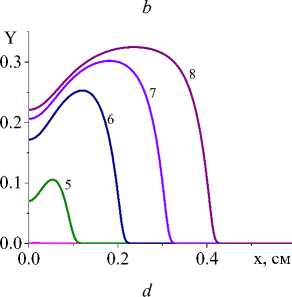
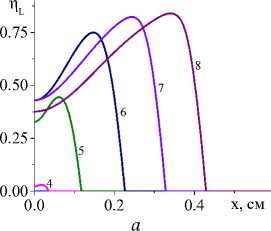
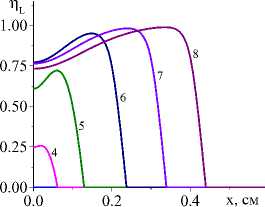
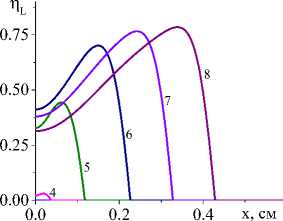
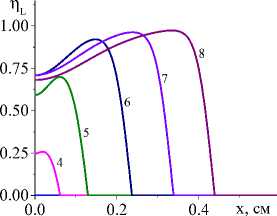
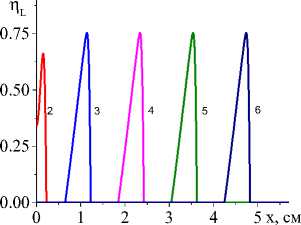
Рис. 3. Распределение степени превращения в последовательные моменты времени: 1) 0,001; 2) 0,004; 3) 0,007; 4) 0,01; 5) 0,02;

• 6)    0,04; 7) 0,06; 8) 0,08 с для вариантов I и IV при q 0 =4 - 10 5 Дж/(см² - с) и a ef =15 Дж/(см 2 - с - К) ( а и c ); при q 0 =5 - 10 5 Дж/(см² - с) и a eff =10 Дж/(см 2 - с - К) ( b и d). Номера кривых соответствуют номерам рис. 1 и 2

Fig. 3. Distribution of the conversion level at successive time moments: 1) 0.001; 2) 0.004; 3) 0.007; 4) 0.01; 5) 0.02; 6) 0.04; 7) 0.06;

• 8)    0.08 s for variants I (pictures on the left) and IV (figures on the right) at q 0 =4 - 10⁵ J/(cm² - s) and a eff =15 J/(cm² - s - K) ( a and c );

at q 0 =5 - 10⁵ J/(cm² - s) and a eff =10 J/(cm² - s - K) ( b and d)

Несмотря на качественное подобие распределения температуры и доли жидкой фазы для разных кинетических функций, степень превращения, которая является основной характеристикой завершенности реакции, ведет себя по-разному (рис. 3). Так, в варианте (I) наблюдается полное превращение в области действия луча и тем раньше, чем выше плотность мощности. При меньшем q 0 в начальной части образца остается непрореагировавший участок. Однако реакция там продолжается до тех пор, пока температура вследствие потерь тепла существенно не уменьшится. В варианте IV полного превращения не наблюдается даже с повышением плотности мощности источника тепла, что и заложено в вид кинетической функции. Заметим, что вид кинетической функции для реакций с участием как твердых веществ (реагентов и/или продуктов реакции), так и жидких может быть модифицирован за счет учета ускорения реакций при появлении жидкой фазы. Например,

ФD (T, Y) = (1 + PnL )(1 - Y)pe-mYY-n, где появившийся параметр должен быть определен из эксперимента или на основе специально сформулированных задач на масштабном уровне взаимодействующих частиц.

В табл. 2 дано сравнение характеристик процесса на квазистационарной стадии для суммарной реакции и разных вариантов кинетических функций. Видно, что различаются не только степень превращения (в вариантах с неполным превращением), но и максимальная доля жидкой фазы и максимальная температура, что говорит о том, что вид кинетической функции отражает особенности механизма химических реакций. Это говорит о том, что учет стадийности превращений также важен для процесса и дает возможность рассчитывать не только распределение температуры, но и следить за изменением состава [37].

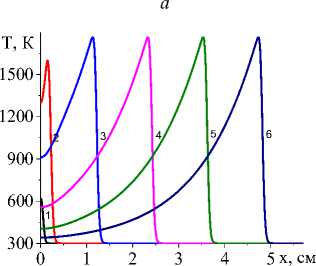
Пример распределения температуры и доли жидкой фазы для системы двух реакций представлен на рис. 4.

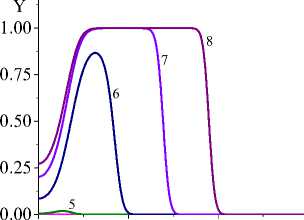
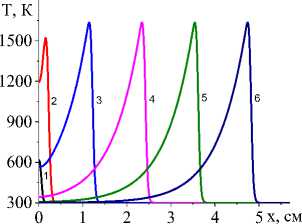
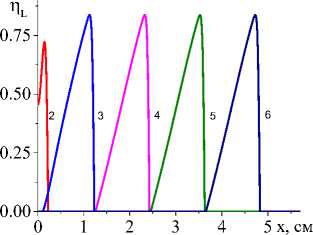
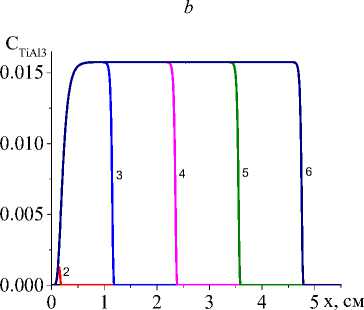
Чем выше коэффициент конвективного теплообмена (рис. 4, а , b ), тем ниже температура, резче температурный профиль, быстрее остывание в области, которую покинул луч, меньше область, в которой присутствует жидкая фаза. Заметно установление неизменных значений концентраций продуктов реакции в квазиста-ционарном режиме (рис. 5, c , d ), а также максимальной доли промежуточного продукта (титана, который еще не вступил в реакцию с алюминием) в области действия лазерного луча (рис. 5, а ). При заданном для примера составе исходной смеси и принятых условиях обработки полного расходования оксида титана не происходит (рис. 5, b ). Алюминий (концентрация которого следует из балансного соотношения) также остается неизрасходованным.

Таблица 2

Сравнение максимальной температуры, доли жидкой фазы и степени превращения для разных вариантов

b

d

Table 2

Comparison of maximum temperature, liquid phase fraction and conversion level for different variants

Вариант	q 0 =4 ⋅ 105 Дж/(см2 ⋅ с)			q 0 =5 ⋅ 105 Дж/(см2 ⋅ с)
	T max , К	V L	Y	T max , К	V L	Y
I	1846	0.879	1	2191	1	1
II	2417	1	1	2959	1	1
III	2334	1	1	2690	1	1
IV	1758	0,827	0,26	2112	1	0,35

Рис. 4. Распределение температуры и доли жидкой фазы в последовательные моменты времени: 1) 0,001; 2) 0,01; 3) 0,06; 4) 0,12; 5) 0,18; 6) 0,24 для варианта V при α eff =20 Дж/(см² ⋅ с ⋅ К) ( а и b ); при α eff =10 Дж/(см² ⋅ с ⋅ К) ( c и d ); q 0 =4 ⋅ 10⁵ Дж/(см² ⋅ с), L S =20 см

Fig. 4. Distribution of temperature and liquid phase fractions at successive moments of time: 1) 0.001; 2) 0.01; 3) 0.06; 4) 0.12; 5) 0.18;

• 6) 0.24 for V -variant at α eff =20 J/(cm² ⋅ s ⋅ К) ( а and b ); at α eff =10 J/(cm² ⋅ s ⋅ К) ( c and d ); q 0 =4 ⋅ 10⁵ J/(cm² ⋅ s), L S =20 cm

На рис. 6 видно, что все параметры модели, которые определяются условиями эксперимента, влияют на характеристики квазистационарной стадии. Например, максимальная температура в зависимости от эффективного коэффициента потерь тепла α eff , толщины подложки h A , начальной пористости θ 0 на квазистационарной стадии изменяется. Зависимость T max от величины плотности мощности источника тепла оказывается линейной.

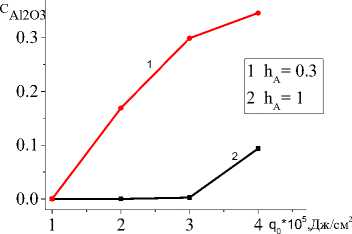
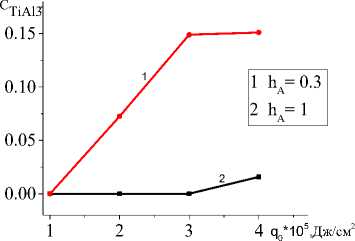
Характеристикой квазистационарной стадии будет и состав продуктов, который зависит от состава исходной смеси и условий синтеза (рис. 7). Влияние подложки продемонстрировано на рис. 7. С увеличением толщины подложки, с одной стороны, изменяется эффективная теплопроводность (увеличивается), что способствует более быстрому прогреву перед движу- щимся лучом. С другой стороны, требуется больше тепла на нагрев до температур, способствующих более полному превращению. Поскольку скорости реакций зависят от температуры, и соотношение между скоростями может изменяться, при более низких температурах, соответствующих низким плотностям мощности и толстой подложке, интерметаллид практически не образуется. При повышении q0 вторая реакция также ускоряется, что и демонстрирует рис. 7.

Заключение

Таким образом, в работе на основе редуцированной модели поверхностной обработки покрытия на подложке показано, что кинетические особенности химических реакций играют важную роль в характеристиках про- цесса на квазистационарной стадии. Особенности процесса на уровне взаимодействующих частиц, отражающиеся через макрокинетические параметры и вид кинетических функций влияют как на максимальную темпе- ратуру, так и на состав продукта. Изучение качественных особенностей процесса синтеза полезно для оптимизации технологии, поскольку позволяет выявить роль основных технологических параметров.

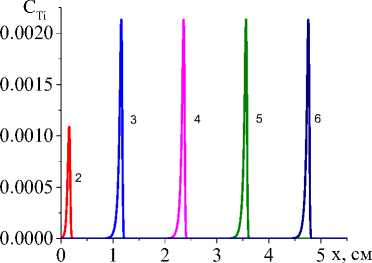
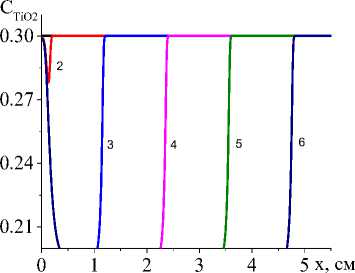
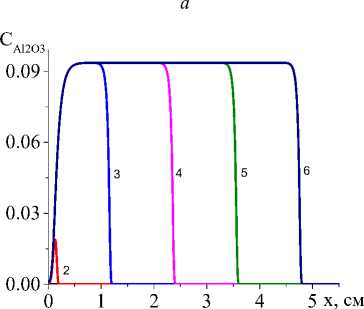
Рис. 5. Распределение концентраций Ti, TiO 2 , Al 2 O 3 , TiAl 3 ( а , b , c , d ) в последовательные моменты времени: 1) 0,001; 2) 0,01; 3) 0,06; 4) 0,12; 5) 0,18; 6) 0,24 для варианта V при α eff =20 Дж/(см² ⋅ с ⋅ К); q 0 =4 ⋅ 10⁵ Дж/(см² ⋅ с), L S =20 см

d

Fig. 5. Distribution of concentrations Ti, TiO 2 , Al 2 O 3 , TiAl 3 ( a, b, c, d ) at successive points in time: 1) 0.001; 2) 0.01; 3) 0.06; 4) 0.12;

• 5)    0.18; 6) 0.24 for V -variant at α eff =20 J/(cm² ⋅ s ⋅ К); q 0 =4 ⋅ 10⁵ J/(cm² ⋅ s), L S =20 cm

  

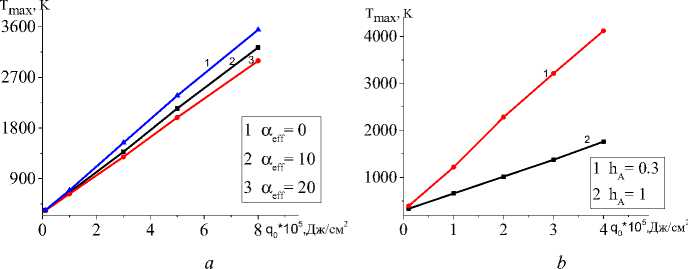
  Рис. 6. Зависимости максимальной температуры на квазистационарной стадии ( а , b , c ) от плотности мощности внешнего источника тепла при разных значениях коэффициента эффективных теплопотерь ( а ), толщин подложки ( b ) и начальной пористости ( c ). В расчете принято C 0 (TiO 2 )=0,3 C 0 (Al)=0,7

  
  
  
  
  

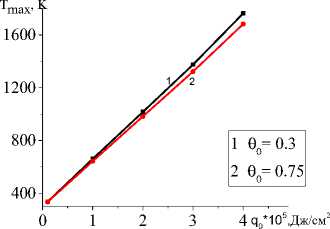
Fig. 6. Dependences of the maximal temperature at the quasi-stationary stage ( a , b , c ) on the power density of the external heat source at different values of the effective heat loss coefficient ( a ), substrate thickness ( b ) and initial porosity ( c ). In the calculation it is assumed that C 0 (TiO 2 )=0.3 C 0 (Al)=0.7

а

b

Рис. 7. Зависимости концентрации Al 2 O 3 ( а ) и TiAl 3 ( b ) на квазистационарной стадии от плотности мощности внешнего источника тепла при разных значениях толщин подложки

Fig. 7. Dependence of Al 2 O 3 ( а ) and TiAl 3 ( b ) concentrations at quasi-stationary stage on power density for different substrate thicknesses