Влияние вида статистического распределения на качество достоверности кривых обеспеченности

В основе решение всех водохозяйственных задач лежат инженерные гидрологические расчеты, наибольшее распространение среди которых получили вероятностные технические приемы, позволяющие рассматривать многолетний ряд наблюдений любой гидрологической характеристики как выборку некоторой случайной величины, функция вероятности которой подлежит статистическому распределению.

При этом устанавливается связь между возможными значениями гидрологической характеристики и их повторяемостью. Для статистической оценки параметров в выборке разработано большое количество способов, среди которых наибольшее распространение в отечественной гидрологии получили метод моментов, метод наибольшего правдоподобия и метод квантилей [1].

Современные компьютеры позволяют автоматизировать (ускорить) расчетные процессы с использованием больших массивов данных, повышая их точность. В настоящее время многими учреждениями и организациями в практике гидрологических расчетов используют несколько программных продуктов - как специализированных компьютерных программ и сложных компью- терных комплексов (Гидростатистика, Гидрорасчеты, HudroStatCalc), так и широко распространенных программных средств общего (Microsoft Exsel) и специального (Statistira) назначения [2].

Определение расчетных гидрологических характеристик осуществляется применением аналитических функций распределения ежегодных вероятностей превышения - кривых обеспеченностей. Наибольший интерес при этом представляет оценка точности расчета выборочных квантилей за пределами выборочного ряда, так как именно они используются в практике гидротехнического строительства для установления значения параметров гидрологического режима, определяющих проектные решения.

Параметры аналитических кривых всегда рассчитываются с погрешностями, что обусловлено недостатком исходных данных и малой точностью аппроксимации эмпирических данных аналитическими кривыми. Точное аналитическое решение определения погрешностей расчета параметров и значений стока заданных обеспеченностей отсутствует. Частичное решение этого вопроса основывается на использовании многочисленных формул, многие из ко- торых не учитывают асимметрию ряда и внутригодовую корреляцию.

Материалы и методы исследования

Для проверки влияния вида функции распределения на качество достоверности кривых обеспеченности были проведены оценки обеспеченности водного стока основанные на формулах Крицкого С.Н. и Менкеля М.Ф., специально разработанных для гидрологических и водохозяйственных расчетов [3], а также на самых упрощённых вариантах функций распределения Виноградова Ю.Б. [4].

В качестве исходных данных использовались значения годовых расходов воды по пунктам наблюдений на р. Свияга. Разовые расчёты, выполненные с помощью программы, написанной на языке Python (версия 2.72), не требовательны к компьютерным ресурсам и проводились, в том числе, на вычислительной технике с процессором Intel Atom Z3740.

Предварительное преобразование исходных данных делалось тремя способами: логарифмированием, возведением в степень с двумя вариантами значений 0.5 и 0.75 с последующей оценкой параметров нормального распределения и обратным преобразованием квантилей нормального распределения.

Использовался метод генерации большого числа подвыборок (500) путём исключения из исходных данных нескольких (5) случайно выбранных значений. Выбор конечного варианта распределения проводился взвешенным усреднением полученных функций распределения [5]. Разброс квантилей распределений и их параметров представлен в независимой от значений форме коэффициента вариации (Сv).

Кроме того, определялась разница квадратов отклонений расчётных обеспеченностей от оценок, вытекающих из исходных данных, полученных по формуле квантилей Г.А. Алексеева, рекомендуемой СП 33-101-2003 [6].

Результаты исследования

Результаты оценок значений обеспеченности и параметров функций распределения с указанием коэффициента вариации (Сv) для пунктов наблюдений Ивашевка, Вырыпаевка, Коромысловка, расположенных на р. Свияга и имеющих ряды наблюдений за стоком продолжительностью от 38 до 66 лет, представлены в таблице. Отклонения расчетных значений расходов воды от практически измеренных в пунктах наблюдений представлены на рисунке 1.

Таблица 1.

Название поста	Трёхпараметрическое гамма-распределение	Нормализация логарифмированием (ln(x))	Степенная нормализация (xn n=0,5)	Степенная нормализация (xn n=0,75)
Ивашевка N=54 min=7.44 max=38,87	обесп.50%=21.5 Сv=0.0149 обесп.5%=37.2 Сv=0.0214 обесп.95%=11.1 Сv=0.0383 обесп.99%=7.98 Сv=0.0413 обесп.1%=45.5 Сv=0.0277 a=0.0618 Сv=0.0616 b=0.896 Сv=0.0216 α=9.82 Сv=0.0655 ∑∆2= 0.114	обесп.50%=21.1 Сv=0.00324 обесп.5%=37.6 Сv=0.00420 обесп.95%=11.9 Сv=0.00855 обесп.99%=9.34 Сv=0.0121 обесп.1%=47.7 Сv=0.00536 s=0.351 Сv=0.0270 ∑∆2 = 0.113	обесп.50%=21.7 Сv=0.00443 обесп.5%=35.3 Сv=0.00553 обесп.95%=11.4 Сv=0.0104 обесп.99%=8.14 Сv=0.0157 обесп.1%=41.8 Сv=0.00652 s=0.777 Сv=0.0212 ∑∆2= 0.094	обесп.50%=22.0 Сv=0.00660 обесп.5%=34.6 Сv=0.00795 обесп.95%=11.0 Сv=0.0170 обесп.99%=7.10 Сv=0.0303 обесп.1%=40.3 Сv=0.00898 s=2.50 Сv=0.0207 ∑∆2= 0.112
Вырыпаевка N=66 min=2.54 max=19.46	обесп.50%=8.66 Сv=0.0128 обесп.5%=15.8 Сv=0.0164 обесп.95%=4.13 Сv=0.0305 обесп.99%=2.87 Сv=0.0390 обесп.1%=19.6 Сv=0.0205 a=0.128 Сv=0.0356 b=0.931 Сv=0.0169 α=7.38 Сv=0.0491 ∑∆2= 0.0211	обесп.50%=8.44 Сv=0.00409 обесп.5%=16.2 Сv=0.00418 обесп.95%=4.40 Сv=0.0117 обесп.99%=3.36 Сv=0.0180 обесп.1%=21.2 Сv=0.00511 s=0.396 Сv=0.0183 ∑∆2 = 0.0493	обесп.50%=8.76 Сv=0.00385 обесп.5%=15.1 Сv=0.00445 обесп.95%=4.13 Сv=0.00867 обесп.99%=2.72 Сv=0.0134 обесп.1%=18.2 Сv=0.00509 s=0.563 Сv=0.0143 ∑∆2= 0.0214	обесп.50%=8.91 Сv=0.00596 обесп.5%=14.8 Сv=0.00676 обесп.95%=3.89 Сv=0.0157 обесп.99%=2.16 Сv=0.0309 обесп.1%=17.4 Сv=0.00745 s=1.45 Сv=0.0151 ∑∆2= 0.0298
Коромыслов ка N=38 min=0.32 max=1.16	обесп.50%=0.636 Сv=0.0196 обесп.5%=1.05 Сv=0.0245 обесп.95%=0.346 Сv=0.0293 обесп.99%=0.252 Сv=0.0314 обесп.1%=1.27 Сv=0.0280 a=1.49 Сv=0.0220 b=0.953 Сv=0.0143 α=10.2 Сv=0.0731 ∑∆2= 0.0649	обесп.50%=0.623 Сv=0.0255 обесп.5%=1.05 Сv=0.320 обесп.95%=0.368 Сv=0.0173 обесп.99%=0.296 Сv=0.0174 обесп.1%=1.31 Сv=0.0775 s=0.320 Сv=0.0233 ∑∆2 = 0.0669	обесп.50%=0.640 Сv=0.00619 обесп.5%=1.02 Сv=0.00725 обесп.95%=0.347 Сv=0.0101 обесп.99%=0.252 Сv=0.0143 обесп.1%=1.20 Сv=0.00801 s=0.128 Сv=0.0213 ∑∆2= 0.0820	обесп.50%=0.647 Сv=0.0105 обесп.5%=1.01 Сv=0.0116 обесп.95%=0.332 Сv=0.0180 обесп.99%=0.218 Сv=0.0295 обесп.1%=1.17 Сv=0.0124 s=0.173 Сv=0.0229 ∑∆2= 0.0926

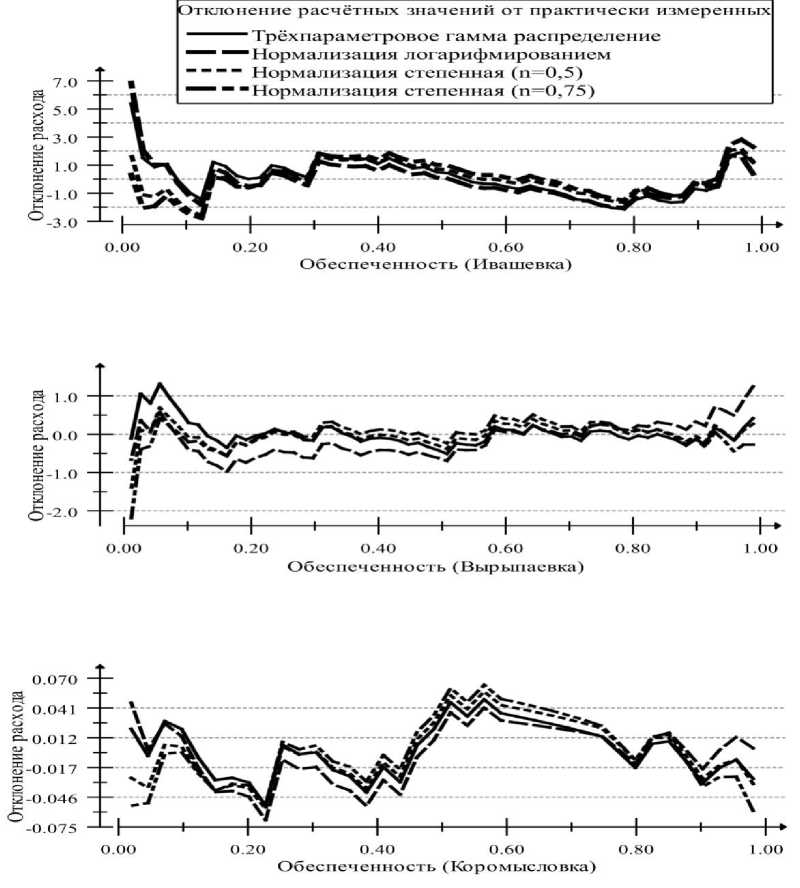
Рис. 1. Отклонения расчетных значений расходов от практически измеренных

Проведенное трёхпараметрическое гамма-распределение и предварительное логарифмирование приводят к сравнительному завышению расчётных значений расходов при обеспеченностях ниже 10%. Нормализация логарифмированием завышает значения расходов воды при обеспеченностях выше 90%.

Степенные функции приводят к небольшому завышению значений 50% обеспеченности. Наиболее равномерно отклоняется от практических измерений вариант с нормализацией степенной функцией при n=0.5. Вывод подтвер- ждается более низким значением суммы квадратов отклонений оценок обеспеченности от практически полученных результатов.

В нашем случае (р. Свияга, пост Ивашевка) нормализация степенной функцией со степенью 0.5 (для участка с высокими значениями обеспеченности) и нормализация логарифмированием (для участка с низкими значениями обеспеченности) дало практически идентичные результаты с расчётом по формуле Крицкого-Менкеля (рисунок 2).

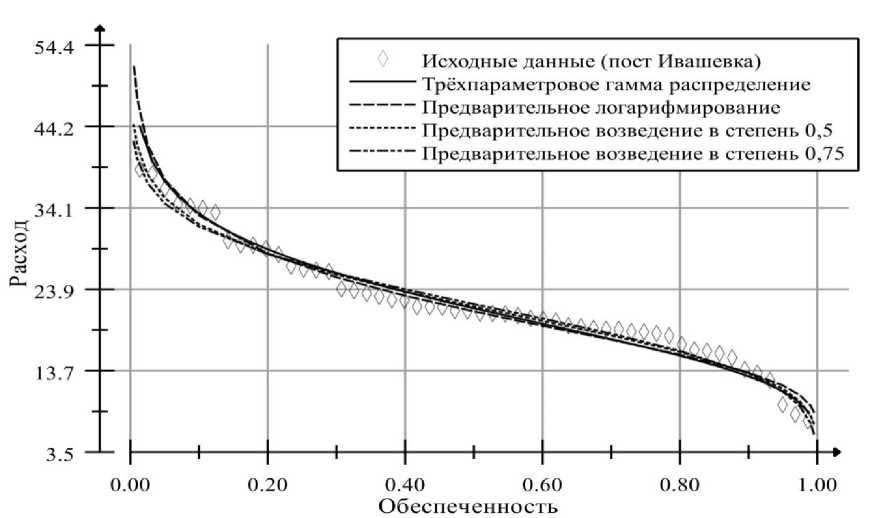
Рис. 2. Параметры распределения исходных данных по посту Ивашевка

Коэффициенты вариации для расчётных обеспеченностей, низкие по сравнению с погрешностями измерения расходов могут объясняться «жесткостью» параметрических функций распределения с малым количеством параметров. Невысокие значения коэффициентов вариации для оценок параметров указывает на их устойчивость при небольшой изменчивости исходных данных, на качество исходных данных и влияние на них объёма исходных данных. Обращает на себя внимание, что при меньшем исходном объёме данных на посту Ко-ромысловка трёхпараметрическое гамма-распределение показало неплохие результаты и существенное снижение коэффициентов вариации параметров.

Заключение

Фактически любая из функций при достаточности данных обеспечивает оценки одного порядка с отклонением, не превышающим погрешностей исходных данных. По этой причине подход с нормализацией исходных данных, обеспечивающий более простой способ оценки обеспеченности, оказывается предпочтительнее, чем расчёт через поиск параметров трёхпараметрического гамма-распределения. Возможно, достаточным будет первичный поиск подходящей нормализации по минимуму суммы квадратов отклонений оценок обеспеченности от практически полученных. Возможен также предварительный поиск оптимального значения n, в том числе перебором с достаточно большим шагом, для степенной функции с использованием любого способа оценки отклонения от исходных данных, в том числе и самого простого по величине суммы квадратов отклонений оценок обеспеченности от практически полученных. Некоторая вариация в подборе параметра n для степенной функции не даст существенно отличающегося результата при расчёте обеспеченностей. Так для оценки влияния параметра n при степенной нормализации на ∑∆2 проводился поиск значения n, для которого ∑∆2 минимально. Для поста Ивашевка при n = 0.35 ∑∆2 = 0.0909, для поста Вырыпаевка при n = 0.48 ∑∆2 = 0.0213, для поста Коромысловка при n = 0.01 ∑∆2 = 0.0662. В последнем случае это минимальное проверенное значение n, при переборе от 0.01 до 0.95 с шагом 0.1. Это может быть использовано для автоматического поиска параметров распределения, в том числе и для перехода от степенной нормализации к логарифмической или к использованию трехпараметрического гамма-распределения.