Влияние вязкостной диссипации водорода и кислорода на температурное состояние пористой пластины

Разработка новых высокотемпературных ГТД с высоким кпд требует увеличения температуры продуктов сгорания. Решение данной задачи возможно с использованием пористых вставок, которые защищают лопатку от более высокой температуры продуктов сгорания. Однако при этом не учитывается диссипация энергии при течении газа через пористую вставку. При определенных условиях (пористость вставки, расход теплоносителя) теплоноситель может вместо охлаждения повысить температуру лопатки. В данной работе предлагается дифференциальное уравнение течения газа через пористую вставку с учётом вязкостной диссипации и программа решения уравнения в системе MatLab. Результаты решения данного уравнения показали, что при уменьшении пористости вставки до 0,02, а также, при неизменной пористости и увеличении расхода (от 1 до 5 кг/(м2с)), температура вставки повышается. При пористости вставки 0,20 влияние вязкостной диссипации отсутствует.

Учёт этих данных позволяет проектировать лопатки газовых турбин с более высокой температурой продуктов сгорания и, следовательно, повысить кпд ГТД.

ИССЛЕДОВАНИЕ ТЕМПЕРАТУРНОГО ПОЛЯ ПОРИСТОЙ ПЛАСТИНЫ

ПРИ ГРАНИЧНЫХ УСЛОВИЯХ ТРЕТЬЕГО РОДА С УЧЕТОМ ВЯЗКОСТНОЙ ДИССИПАЦИИ

Рассмотрим температурное поле в пористой стенке при эффузионном охлаждении при гра- ничных условиях третьего рода.

Предполагается [1, 2], что температура стенки равна или выше температуры охладителя. Учтем выделение тепла вследствие прокачки теплоносителя через пористую стенку и обозначим qтр, тогда уравнение баланса тепла запишется в виде:

qx+dx– qx– dqo+ dqтр=0,              (1)

где: q = - 2 (1 - П ) ^f dt- 1 x            V dx )

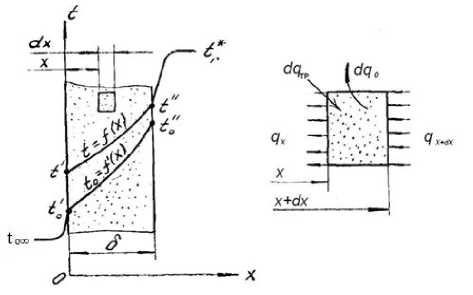
Рис. 1. Температурное поле в пористой стенке при граничных условиях третьего рода и с учетом выделения тепла за счет трения q , = -X(1 - П) |     | x + dx                  ,/r       , ,

< dx v x + dx где П – пористость пластины.

Используя разложение по формуле Тейло ра, и ограничиваясь бесконечно малыми вели чинами первого порядка малости имеем:

-

1 dt ₀

где: t =         ⁺ t

B dx

q , = -X(1 - П) f dt- I x+dx v dx V x + dx

= x (i - n ) ^f dt + d^t V dx dx

,

x

dqo=av(t-to)dx, dp qтр= – vdp= –

.

p

Тогда (1) будет иметь вид:

d ² t                 dp

^{X p} ——p ⁺ a o⁽ t ^- t o ) +-- — = ^o . ⁽²⁾ dx              p dx

-

x x = —; 5	0 o	t «.          t - t f
		;                                  ; t г            t-- t f
dt o = t1	- t f	d 0 o d 2 1 o = t - t t f	d 20o
dx d 3 1 o = dx 3	5 t '- 1 53	dx ’ dx 5 3 f u 0 o dx 3	dx 2 ,

d ® o. + B - d^ ^ o

A—

BC 5

BC

t — t f

,

Используем уравнение течения газа через пористое тело:

dp Yep = aMoGo + ^G2 = a^oGo- + ^G^-. (3) dx               g gpcp g pep подставляя (3) в (2) находим:

-   1 d 0_O -

0 =-- ° + 0_n

0 ,

Х(1- П)

_d 2 _t

+ a ₂( t - 12) + ^a^^!G ² + e L gp p p g p cp p

d ³0   dd ²0 o

+ b dx 3dx 2

Ad ^ = bc

,

= 0. (4)

Учитывая уравнение энтальпий dqo=GoCpodto,

где Go, – массовый расход охладителя, сpo – средняя по толщине стенки изобарная теплоемкость охладителя.

где: A = A5²

a 5 ² —

—v— , B = B 5 =

Xp

a v 5

c_{p 0} G ₀

,

где A =

a dt o = v dx     G0cp0 ,

BC = BC--- t '- tf

^a o ^a o ^p o ⁵ G o

a в 5 G

c p o ^p ( t ^,- t f ) ⁺ c p o p g ( t ^B- t f ) .

Решение уравнения (12):

d2t dx2

dt ₂ dx

« v

Xp ’

^^^^в

A ( t

^^^^в

t ₂ )

= C ,

0 o = С 1 + С 2 e^{a 2} x + C 3 e a ^{3 x} + 0 o част , (13)

где:       = OX д     0част

в

B ( t

B =

в

t 2 ) ,

'

"

Из 0n

0 част

0 част

0n

0 част

«v cp0G0

,

_C = a o P o G o ² ₊ P o G o ³

^Xpp o ^{2    X p}p o ² g ■

Преобразуем систему уравнений. Получаем уравнение вида:

_BC a = —— A

avMo5Go cPo po2 ( ttf )

/5

c p o P o² g ⁽ t '^- t f ) , ⁽¹⁴⁾

0 _o = С 1 + С ₂ e^{Q 2 x} + C 3 e^{a 3 x}

BC

A x .    (15)

d ³ t ₀        d ² t ₀

+ B dx 3       dx 2

A dt = BC ,     (9)

dx

где: a1, a2, a3 – корни характеристического уравнения,

a3+k1a2+k2a=0/

Из (16) непосредственно следует, что а1=0,

a 2,3

^^^^^^в

k1

k1 ±J^- + кг , a 242,

' 2,3

^^^^^в

a „ 8

±, c_{p 0} G ₀

а⁸ I + а ^{8 2}

C p о G о J     Xp '

0 част

– одно из частных решений.

Составим уравнение для определения постоянных интегрирования:

при x=0

а о ( С ; + С 2 + С з — 0„ ) = X

a 2 C 2 + a з C з — a

C 1 + C ₂1 1

^^^^^^B

Xr 2 а о ⁸

+ C ₃

Xr ₃ )

I = 0< ^а 0 ⁸ J

Xa

при : x=1

«( 0 *г — 0 ”) = (X p (d 0 /dx) x=i ] / 5,

(    + ( e (1 + X р Г 2 / a _r5) + С з е^а3(1 + X р З з / a _ 5) =

= 0 *г — X p a/ 5

при: x =0

((d^{2 0} /dx²) x =o - a v 5² ( 0 ‘ - 0 o” )]/ X p -0.

		Г	X „	7 a	^		г	Х Р	a 32	^
С 1	+ С 2	1	P	2		4- С	1				= 0 п 0 ^
		<	а V	8 2	J	+ C 3	к	а у	8 2	J

Запишем систему уравнений в виде, удобном для представления определителей:

C 1 ⁺ ^G-^) ⁺ ^G-^) ^- 0 Ooo - d, C₁ + C₂(1+b_гa₂)e^r2 + C₃(1 +b_гa₃)e^r3= _г–d,

C1 + C2(l - bva22) + ^(1 -      ) 0Ooo, где: b = 3; b = X; b = _3^; d = M_

0 а08   Г аГ8   V aV82

Тогда определитель имеет вид:

¹ G-G^)    ^(1-Ь о ^а з )        0 0oo - ^d

1 (1+bra2)er2 (1+bra3)er3

1 (1-bva22)   (1-bva23)

Постоянные интегрирования:
С = а с ; С 1     а ’	А С 2 С2 = Д ,	г дс ^ 3 =—, где: Д
	0 о? (1 - b0a2)	(1 - b0a3)
ΔC1 =	(1 + Ьг а 2 г	) e a 2     ( 1 + b2c 3 ) e a
	a 2 b 0 о? (1 - 2V)) d	a 2 b (1 - 3 v ) d
	1           0 о?	(1 - b0a3)
ΔC2 =	1         ё г	( 1 + bra 3 ) ea 3
	1           0 о?	a 2 b (1 - 3 v ) d
	1       (1 - b0a2)	0 o?
ΔC3 =	1      (1+ Ь г а 2 ) e a	0" г
	a 2 b 1       (1 - 3 v ) d	0 o?
	1       (1 - b0a2)	(1 - b0a3)
Δ =	1     ( 1 + ba ) e 2	( 1 + b2a 3 ) e a
	a 2 b 1       (1 - 2 v ) d	a 2 b (1 - 3 v ) d
b = ^^ 0 а8	b = 3 1    ь = г      e      и а г о	^^ d = 1 — аи8	а 0 g 0 c P 0

Таким образом, получено уравнение, описывающее тепловое состояние пористой стенки, которое учитывает подогрев пористой стенки за счет трения теплоносителя о поверхность пористого тела. Показано, что возможны режимы течения теплоносителя, при которых его темпе- 0

а)              x

б)          x

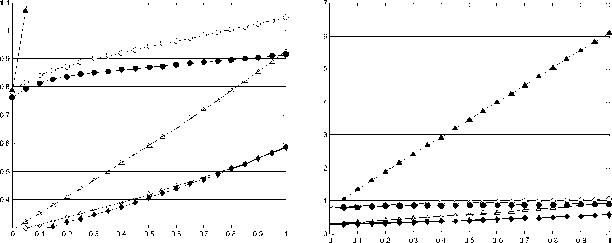
Рис. 2. Влияние пористости при G=1:

а) кислород- «-11=0.2; о-П=0,05; водород - 0-11=0,05; ♦ -11=0,20; Д - П=0,02

б) кислород- е-П=0.2; о-П=0,05; ▲-11=0,02 - водород - 0-11=0,05; ♦ -11=0,20; Д-11=0,02

Θ

Θ

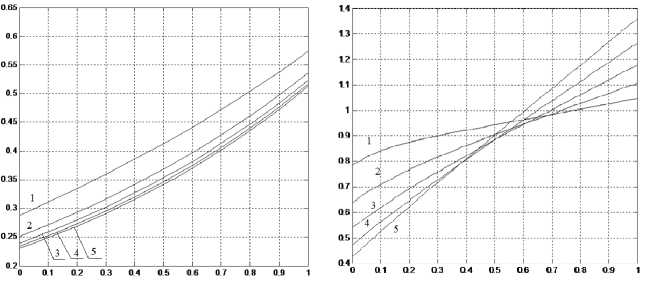
а)               X                  б)             X

Рис. 3. Влияние расхода при П=0,05:

а) водород; б) кислород “1 - G0=1 кг/(м2.c); 2- G0=2 кг/(м2.c);

3- G0=3 кг/(м2.c); 4- G0=4 кг/(м2.c); 5- G0=5 кг/(м2.c)

ратура может превышать температуру пористой стенки. Кроме того, что температура теплоносителя выше температуры пористой стенки, тепловой поток будет направлен в стороны пористой стенки, и тем самым температура пористой стенки будет возрастать.

С помощью программы, разработанной на языке MаtLаb, решена система уравнений (5). Рассматривался газ H₂ , О₂. Исходные данные для решения этой системы уравнения включают следующие величины: λ=121,4 Вт/(м·К), П=0,02; 0,05; 0,2; λ_с= λ(1-П); t’’=600^oC, С водород =14300 Дж/(кг^с·К); С_p кислород = 980 Дж/ (кг·К) , G₀=(1, 2, 3, 4, 5) кг/(м²·с), δ=0,01 м; α₀=10⁴ Вт/м²К; α_r=10⁴ Вт/м²К; α _v =10⁶ Вт/м³К.

Считаем, что эти величины постоянны и не зависят от температуры.

ЗАКЛЮЧЕНИЕ

Из полученных результатов видно, что при уменьшении пористости скелета увеличивается его температура. Средняя разница в температуре по всей длине пластины между П=0.2 и П= 0.05 для кислорода 7, 661% , а для водорода 3,176%.

При П=0.02 заметно резкое увеличение температуры скелета к его наружной поверхности, в отличие от П=0.05 составляет для кислорода в 6 раз, для водорода на 30%.

При увеличении расхода водорода температура водорода падает, а кислорода к поверхности пластины возрастает.