Влияние внешних случайных возмущений на параметры замкнутого вентильного электропривода

Возмущения, действующие на электропривод, - колебания напряжения силовой сети V, (?) и момент статической нагрузки М_п^ - в данной работе представлены случайными величинами соответственно К, и М_ст.

Пусть заданному углу регулирования а и номинальному напряжению силовой сети, И = 0, соответствует рабочая точка А на естественной статической характеристике силового блока вентильного преобразователя, кривая 1 на рис. 1.

Рис. 1. Влияние колебаний напряжения сети и момента статической нагрузки на положение рабочей точки силового блока вентильного преобразователя

Статическая характеристика силового блока вентильного преобразователя Е(а) описывается следующим выражением:

E = E0-cosa. (1)

Коэффициент передачи солового блока найдем из формулы (1), переписав ее следующим образом:

. к = — = -Ео -sina = -Je^-E; , (2) 8a ° ° А где Ед - значение выходной ЭДС преобразователя Е в точке А.

При понижении напряжения силовой сети на величину J^ характеристика £(«) изменит свое положение и будет изображаться кривой 2 (рис. 1). Рабочая точка преобразователя при этом переместится из А в В, где согласно выражения (1) ЭДС Е = Е_В будет меньше Е_д на величину Р, - cos а, а коэффициент передачи запишется

К = . (3)

Рассмотрим изменение коэффициента передачи К при работе вентильного преобразователя в электроприводе с замкнутой астатической САР поддержания заданной скорости и (ЭДС Е_о ) двигателя.

При работе электропривода на холостом ходу (х.х.), если пренебречь током х.х., ЭДС преобразователя Е равна ЭДС двигателя Е_д. Тогда при ^ = 0 согласно формуле (2)

K = -V^-£L (4) Если рабочая точка преобразователя при этом находилась в А, то при понижении напряжения силовой сети на величину Р, она будет стремится перейти в точку В. Однако под действием САР ЭДС преобразователя восстанавливается до значения Е_д. Рабочая точка при этом переместится в С, где коэффициент передачи силового преобразователя

K = J(£_q-£)²^E^ . (5)

При появлении нагрузки на валу двигателя, чтобы поддержать скорость неизменной, САР изменит ЭДС преобразователя на величину К2, равную падению напряжения в силовой цепи преобразователь-двигатель / • гя. Рабочая точка преобразователя при этом переместится в О, а коэффициент передачи в данной точке будет

К = -^„-РОМД^# • (6)

Таким образом, коэффициент передачи силового блока вентильного преобразователя в данном случае уменьшается не только за счет снижения напряжения сети на величину ^ , но также и из-за падения напряжения в силовой цепи, вызванного током нагрузки двигателя.

Повышение напряжения сети на величину Г, будет, наоборот, вызывать увеличение коэффициента передачи. В выражениях (5) и (6) при этом перед У_х будет стоять знак плюс.

В общем случае при Е_д = const

К = -^(Ео + ^)2~(Ед + УгУ =К(УХ,У2У Ю

Выражение (7) имеет смысл при выполнении неравенства

(Ед + У2У <(ЕО+УХУ.(8)

Так как суммы стоящие в скобках обеих частей неравенства положительны, то можно записать

Ед + У2<Е0 + Ух,(9)

ИЛИ

Уг-УХ^ЕО-Ед.(10)

Из рис. 1 видно, что при снижении напряжения сети на величину Ух и появлении падения напряжения в силовой цепи У2 угол регулирования а сначала уменьшается до значения а,, а затем - до а2. В результате, коэффициент передачи К снижается и при а = 0 К = 0. Равенство коэффициента передачи нулю будет иметь место при выполнении соотношения

У2-Ух>Е0-Ед.

(Н)

Таким образом, коэффициент передачи силового блока вентильного преобразователя, работающего в электроприводе с замкнутой астатической САР,

-^(Е₀+У_х)²-(Е_д+ку², если У_г-V, <Е_й-Е_д,_№)

0,

если V₂ - Т, > Е_о - Е_д

представляет собой, при Ед = const, функцию двух случайных аргументов Ух и У2. Нелинейная зависимость коэффициента передачи от величин Ух и У2 обусловлена нелинейным характером статической характеристики силового блока преобразователя Е(аУ

В связи с тем, что рассматриваемая функция ^(^^г) является нелинейной, то наиболее исчерпывающей информацией о ее поведении в зависимости от значений случайных величин У_х и У_г будет служить функция распределения Е(К^ или плотность вероятности /(К).

Для удобства последующего анализа и большей общности полученных результатов пронормируем уравнение (12) относительно Ео, тогда получим

ЦУ„Уг) =

-^^-(Е^Уу¹, если У_г-У_х<1-Е_д, ₍₁₃₎ .   0,          еслиУ₂-У_х >1-Е_д.

Учитывая, что функция К(У_Х,У₂) не знакопеременная, можно рассматривать ее по модулю. На основании вышесказанного и формулы (13) построена область определения функции К (У,, У₂) на плоскости У_х0У₂ (рис. 2). Положение верхней границы области зависит от величин К и Е_д. При фиксированном значении Е_д указанная граница будет тем выше, чем больше коэффициент передачи К . Положение нижней границы - прямой линии, соответствующей уравнению

У_г-У_х=1-Е₆, (14)

зависит только от значения ЭДС двигателя Е_д . На этой границе и ниже коэффициент передачи преобразователя равен нулю и, следовательно, система электропривода размыкается. На полуплоскости, расположенной ниже прямой (14), функции Г (ку и f(K^ равны нулю. Следовательно, на основании вышесказанного [1],

FW = ^ ^г) с G) = ^f(Vx, V2)dVxdV2, (15) G то есть, вероятность того, что случайная точка (УРУ2) попадет в заштрихованную область С.где выполняется неравенство К ( Ух, У2) < К, равна двойному интегралу по области G от совместной плотности вероятностей системы величин (УХ,У2). Здесь К - значение коэффициента передачи на верхней границе области G, а К(У,,У2)- его значение внутри области G.

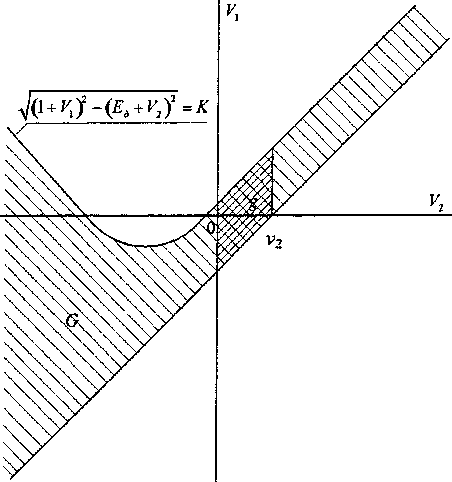
Рис. 2. Область определения функции К(Ц,У2)

на плоскости V,0V2

Электромеханика

Для определения пределов интегрирования в формуле (15) на основании уравнения кривой верхней границы области G (см. рис. 2) найдем выражение для К,

K.^+f^+Fj2 -1.

Тогда на основании равенств (15), (14) и (16), запишем

чин (У„У₂), а также значение ЭДС двигателя £_д, полученные экспериментальным путем на непрерывном среднесортном прокатном стане 350/500 Златоустовского металлургического завода:

т, = 0, т₂ = 0,12 , ст, = 0,01-^0,03 ,

<т2 =0,01-г 0,03, г]2 =-0,67 и £д =0,796.

FW

J /д,та

dy2.

Дифференцируя выражение (17) по переменной К, входящей в верхний предел внутреннего интеграла, получим дк)= j_JL=/№^^-^^ Af2■ (is)

-д№+(С+С) v >

Область определения функции К(Е,У₂) G, где случайная величина У₂ изменяется от -со до со (см. рис. 2), носит сугубо теоретический характер. На практике же падение напряжения в силовой цепи F₂, как и ток двигателя, не знакопеременная величина. Для нормальных режимов работы вентильного электропривода непрерывных прокатных станов, когда ток двигателя не превосходит допустимых значений, величина У₂ изменяется в пределах от нуля до 15...20 % по отношению к ЭДС Е_о (в относительных единицах). В связи с этим реальная область определения коэффициента передачи силового блока вентильного преобразователя (см. область g на рис. 2) по переменной У₂ ограничена осью ординат и некоторым положительным значением этой переменной У₂ = v₂. Пределы -со , со в интегралах (17), (18) изменятся соответственно на 0, v₂.

При нормальном распределении случайных величин К, и У₂, совместная их плотность распределения, то есть плотность распределения случайного вектора (У_1;У₂), запишется

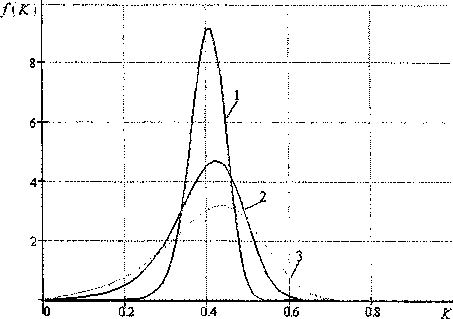
Рис. 3. Плотность распределения коэффициента передачи силового блока вентильного преобразователя при 1) о, = а₂ = 0,01; 2) а, = 0,01; а_г = 0,03 ; 3) а_А=а₂ = 0,03

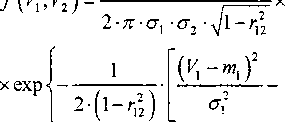
г-г,,-^-^)-^-^) ! (^-^)² , ₍₁₉₎ 0*2 " О"₂ О 2

Решение интегралов (17), (18) с учетом выражения (19) может быть получено только численными методами.

На рис. 3 приведены графики плотности распределения коэффициента передачи К . При этом использованы параметры системы случайных вели-

Как следует из графиков рис. 3 с увеличением степени рассеивания случайных аргументов К, и У₂ закон распределения /(.К) существенно деформируется. Так, при относительно малом рассеивании аргументов (ст, = о₂ =0,01, кривая 1) плотность вероятности /(К) близка к нормальному закону. По мере увеличения параметров ст, и о_г плотность вероятности /(К") все больше отличается от нормального закона, при этом значительно возрастает отрицательная асимметрия (кривые 2 и 3), а мода несколько уменьшается. Как следствие, коэффициент передачи вентильного преобразователя приближается к нулевым значениям, что может привести к размыканию САР электропривода. Это особенно опасно для непрерывных прокатных станов. А именно при размыкании САР происходит нарушение соотношения скоростей соседних клетей, в результате чего происходит либо разрыв прокатываемого металла, либо наматывание его на валки стана, а это означает крупную аварию с опасностью для жизнедеятельности персонала и значительные экономические ущербы.

Выводы

С точки зрения улучшения энергетических показателей вентильного электропривода необходимо устанавливать угол регулирования а как можно меньше, так как он приблизительно равен углу сдвига между током и напряжением в питающей сети. Тогда уровень потребления реактивной мощности из сети будет минимальным. С дру-

гой стороны для улучшения динамических свойств и надежности работы вентильного электропривода угол регулирования а должен быть как можно больше. Таким образом, здесь приходится иметь дело с двумя взаимоисключающими факторами. Для того чтобы эти факторы сбалансировать, необходимо решить оптимальную задачу. Результатом решения такой задачи должна быть вырабо тана четкая рекомендация по установке начального угла регулирования a , что равносильно выбору оптимального запаса по напряжению вентильного преобразователя.