Влияние внутренних смещений на упругие модули монослоя графена в дискретно-атомистическом подходе

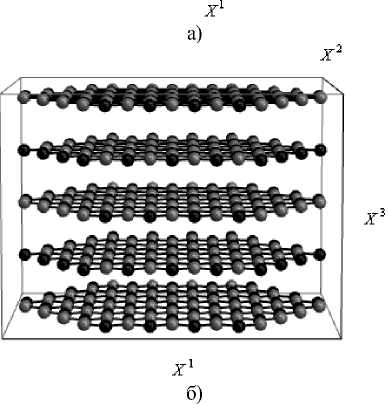
Рис. 1. Геометрическая модель: а) графена, б) гексагонального α-графита. Атомы двух разных подрешеток изображены черным и серым цветами

Несмотря на разнообразие потенциалов, применяемых для описания ковалентных связей атомов углерода в графене, существует значительное расхождение экспериментальных значений упругих модулей графена и расчетных оценок, связанное с тем, что при идентификации параметров потенциалов не учитываются механические свойства графена [2].

В [2] также приводится обзор экспериментальных методик по определению упругих свойств решеток графита и графена, начиная с исследований [3, 4]. Данные многих экспериментов получены не напрямую, а из дополнительных расчетов с помощью той или иной модели упругого изгиба пластины [5], поэтому разброс экспериментальных данных часто вызван приближенным характером модели, выбираемой для обработки экспериментальных измерений.

Таблица 1. Данные разных исследователей

Для теоретической оценки упругих свойств графена используются потенциалы Тер-зоффа [11], Бреннера первого и второго поколения [12, 13], потенциал AMBER [14, 15], многочастичные и моментные потенциалы, упругие стержневые системы с учетом изгибных жесткостей и жесткостей при изменении углов между стержнями [2, 16-20]. Несмотря на довольно большое число параметров этих моделей, с их помощью не удается получить набор механических характеристик графена, который бы давал совпадение с экспериментальными значениями для всех свойств. Существование произвола в выборе параметра толщины слоя графена приводит к возможности подобрать любое значение трехмерного модуля Юнга. Для нанотрубок подобная особенность называется парадоксом Якобсона [21, 22]. Однако безразмерный коэффициент Пуассона не зависит от толщины слоя, и в этом параметре наблюдается наиболее значительное отклонение расчетов от экспериментально определяемой величины и большой разброс теоретических оценок. Можно встретить значения, превышающие ν=1 [23], что противоречит условию положительной определенности тензора линейно-упругих свойств двумерной среды. Важной особенностью расчетов является наблюдаемое в ряде работ нарушение изотропии упругого отклика графена. Большинством авторов используется прямоугольная форма образца, что приводит к появлению ортотропии упругих свойств монослоя графена в его плоскости [19, 24, 25] и противоречит известным результатам теории упругости. В частности, в [19] в зависимости от вида деформирования (направления оси растяжения и простого сдвига) получены качественно разные наборы значений упругих модулей, вплоть до смены знака коэффициента Пуассона. В расчетах по изгибу прямоугольного и круглого листа графена сосредоточенной силой также обнаружена зависимость упругих свойств от формы образца и от его размеров [20], что подтверждается рядом экспериментов [21]. Зависимость упругих модулей от размеров образца также подчеркивалась в работе [26].

Цель работы: демонстрация возможностей простейших потенциалов семейства Ми [27, 28], содержащих безразмерные степенные параметры, для расчета упругих свойств графена, в том числе, в рамках несимметричной постановки задачи линейной теории упругости.

Объектом исследования является монослой графена конечного размера без использования периодических граничных условий. Используется статический подход [29-31], в рамках которого рассматриваются малые искажения тела. При этом вопросы об устойчивости решетки или изменении направления ковалентной связи при деформировании решетки графена не исследуются. При задании потенциала межатомного взаимодействия вводится два различных слагаемых, отвечающих за притяжение и отталкивание атомов. Принимается, что система ковалентных связей учтена структурой кристалла, а по ней с помощью бесконечно малых искажений определяются его упругие свойства.

Определение начальной конфигурации монослоя графена. Для исключения эффекта от наложения классов симметрий образца и решетки, вычислительные эксперименты проводятся с образцом графена, форма которого, как и решетка графена, имеет ось симметрии третьего порядка, например, рис. 1а содержит образец графена с N=4 атомами на стороне. Структура кристалла в любой конфигурации считается однородной по образцу и полностью характеризуемой значением параметра а межатомного расстояния в любой из треугольных подрешеток графена. Однородная деформация кристалла, как изменение длин и углов между отрезками прямых, соединяющих атомы, описывается однородным аффинором (или тензором деформаци- онного градиента) F, используемым в механике сплошных сред. Если Rk — радиус-вектор произвольного к-го атома образца в начальной конфигурации, то в текущей конфигурации его положение задается вектором rk = F • Rk (правило Коши-Борна [24, 32]). Аффинные деформации накладываются на образец в естественном ненапряженном и недеформированном состоянии. Отсчетная конфигурация задается только значением параметра межатомного расстояния a, определяемого из условия минимума полной потенциальной энергии Ф(a)|F=I, I — единичный тензор второго ранга:

Ф( a ) f=i

^ min a

M-1  M ф Z ^ф*(Rk -Rj) + Z ф-(Rk -Rj) j=1 у k=j+1                        k > j, k e Sj

R k , R j e A

где M - число всех атомов образца, A - двумерная область, содержащая его атомы, ф * ( R^ - R ) - часть потенциала, отвечающая за отталкивание атомов, ф^- ( R_t - R ) - его часть, связанная с притяжением, S j — множество номеров атомов, составляющих ближайшую окрестность j -го атома и связанных с ним ковалентными связями. Для описания взаимодействия атомов графена выбирается простейший потенциал семейства Ми [27, 28], содержащий два слагаемых степенного вида, которые характеризуют притяжение и отталкивание атомов. Показатели степени в этих слагаемых описывают убывание интенсивности взаимодействия с расстоянием:

ф( r ) = в (n (а / r) m - m (а / r) "j/(m - n)

,   (2)

где а - равновесное расстояние для изолированной пары атомов, в - энергия, соответствующая глубине потенциальной ямы при взаимодействии двух таких атомов. За притяжение отвечает часть ф ( r ) = -в m ( а / r ) /( m - n ) , за отталкивание — часть ф * ( r ) = в " ( а / r ) /( m - n ) . При m =12 и n =6 (2) дает известный потенциал Леннард-Джонса [27,28].

Условие (1) при выборе потенциала (2) позволяет получить точные выражения для равновесных значений межатомного расстояния и полной потенциальной энергии в естественной конфигурации образца для произвольных параметров потенциала. При использовании нормированного межатомного расстояния b< jk ) ~ r ( jk ) / a , ^r ( jk ) = |^r( k ) - ^r ( j ) I получим:

1/( m - n )

a

а

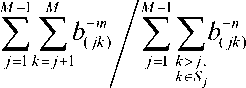
ФJ

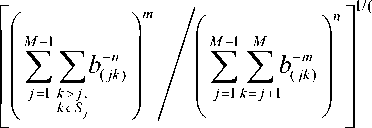
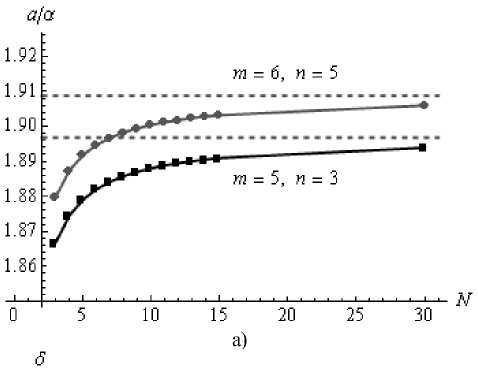
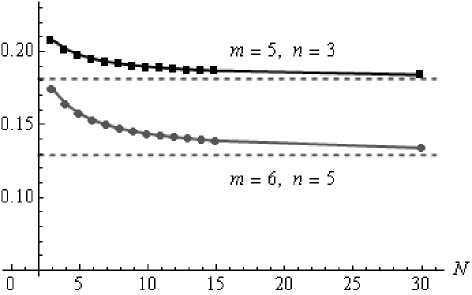
Выбирая различные значения безразмерных параметров m и n, можно получить набор выражений для начального межатомного расстояния a через параметр а потенциала Ми в виде a = g(m, n, N) а, где коэффициент пропорциональности g зависит не только от m и n, но и от числа атомов N на стороне образца, то есть от его размера. Примеры зависимостей безразмерного комплекса a / а от числа атомов N для двух наборов значений параметров m и n приведены на рис. 2а. Найденные числовые последовательности быстро сходятся к асимптотическому значению. При получении для них приближенной функциональной зависимости использовался класс функций y = c (x - x0)k + b. Параметры c, к, b, xо определялись методом наименьших квадратов, причем оказалось, что для всех исследованных значений m и n параметр к с высокой точностью совпадает со значением к= - 1, параметр b характеризует положение горизонтальной асимптоты и связан с параметром решетки представительного образца или макроскопическим значением a" / a ь. Предельное расстояние между атомами в подрешетках a выражается для двух наборов m и n как

1) m=6, n=5: a ^∞=1,909 a 2) m=5, n=3: a ^∞=1,897 a (3)

Значение параметра a , приводимое для графена в справочной литературе, составляет a ^exp=1,42 x 10^-10 (м). Это расстояние выражается через найденное предельное расстояние между атомами одной подрешетки как _a ^exp = _a ” / Vs • Тогда для заданных степеней m и n параметр α идентифицируется как

• 1)    m=6, n=5; α =1,29x10^-10 (м)

• 2)    m=5, n=3: α =1,30x10^-10(м)

Анализ несимметричного упругого закона. Рассматриваются чистое растяжение-сжатие вдоль произвольной оси     l ,

F = I + (X -1)ll (l — единичный вектор, X — кратность удлинения), и простой сдвиг F = I + у bn интенсивности у в плоскости с нормалью n в направлении b. Площадка dS при деформировании        переходит        в ds = J (n • U-2 • n)1/2 dS, где J = det F, n — нормаль к малому элементу поверхности в текущей конфигурации, U — правый симметричный тензор из полярного разложения аффинора F = R • U, R — собственно ортогональный тензор [33]. Для несимметричного случая используется следующая форма закона Гука (искажения и повороты малы):

° = C ^{:( F} - I - w # ) ,     (6)

где w # — кососимметричный тензор малого поворота кристаллической решетки. Такая форма гарантирует выполнение условия материальной индифферентности закона Гука в несимметричной постановке при малых искажениях. Мера деформаций, появившаяся в правой части (6), соответствует мере, предложенной для больших деформаций в работе [34]. Упругая энергия в рассматриваемом несимметричном случае при малых искажениях имеет вид:

u = 2^{( F} - ¹ - w #^): C ^{:( F} - ¹ - w # )    (7)

Анализ строения тензора C дает 3 независимые ненулевые компоненты:

c  c  c

1111  ^1122 ^1212

Условие симметрии тензора C для графена записывается как

^-1212 = ( ^- 1111   ^C 1122^)/2

Модуль Юнга E и коэффициент Пуассона v используются для сравнения расчетных и экспериментальных значений и для двумерной среды равны л с(s,s) V   f c(s,s) V

4 ц ( X + ц )    ⁽ C 1111 )   ^{( -} 1122 )

X + 2 ц =     -^

X v =-----

X + 2ц

р ^(s,s)

е ( - 1;1)

(s,s)     v       7

C

,

где X и ц — постоянные Ламе, а тензор C ^(s,s) — полусимметричная часть C , то есть обычный тензор ^(s,s)          /^(s’s)        r^s’s) rt^s,s)

упругих модулей. Ограничения (10) (или - 1111 >  0 , — ₁₁₂₂ ^G ( - — 111 ; - 111 ) ) на значения упругих характеристик обеспечивают положительную определенность тензора C ^(s,s) .

Определение компонент тензора C для решетки графена. Плотность упругой энергии (7) при двухосном растяжении принимает вид:

и = 1 - 1111 ( X - 1) ² + 1 - 1111 ( X 2 - 1) ² + - 1122 ( X - 1)( X 2 - 1)

При простом сдвиге в плоскости образца плотность упругой энергии равна:

u = 2^{( -} 1111    ^- 1122    ^- 1212 ) У

.

Для вычисления упругих модулей (8) слоя графена вычисляется полная потенциальная энергия кристалла в текущей конфигурации ф ( F , N ) , делится на площадь деформированного слоя и приравнивается плотности упругой энергии:

w N)= Z Z ф+ (r - r)+ Z Ф- ^ - r = F ■ Ri  R e A

,                         ,                ,

y(F, N) = ф(F, N)/ s s = J (n ■ U-2 ■ n)1/2 5  5 = a2 NХз^З 2

V ( F , N ) = u

При любой деформации F , оставляющей монослой графена в его плоскости, площадь слоя s = 3V3 J a ² N ² / 2 . При двухосном растяжении-сжатии J = X 1 X ₂, в условиях малых искажений J «X_x+X^- 1, при простом сдвиге ^J = ¹. С использованием (13) и (11) в случае двухосного растяжения-сжатия, вычисляются две компоненты тензора линейно-упругих свойств:

С =

д 2у

ах 2

X] =^ 2 =1

д ² у 6Х[

с

д2 v ах, дх2

X 1 =X ₂ = 1

С использованием (13) и (12) при простом сдвиге вычисляется выражение

С -С

1111   ^1122

с =

д 2v

Первые производные по параметрам деформирования при условии λ 1 =λ 2 =1 или при γ=0 равны нулю, что гарантируется заданием начальной конфигурации, соответствующей минимуму полной потенциальной энергии образца. Таким образом, для различных значений параметров m и n при различном числе атомов N на стороне образца графена могут быть независимо определены все 3 упругих модуля (8).

Внутренние смещения. При действии аффинора на начальную конфигурацию монослоя графена обе его подрешетки деформируются одновременно, что приводит к нарушению симметрии расположения атомов одной подрешетки относительно атомов другой. Следовательно, решетка графена при заданной аффинной кинематике не всегда может деформироваться однородно. Для графена необходимость учета внутренних смещений подрешеток отмечалась в статье [32]. В данной работе получено, что вектор внутренних смещений представляется в виде:

ay2

Y=0

б = {Sj; б₂; 0} = 5 (e₁e₁e₂ + e^e - ^e2^ei^ei + e₂e₂e₂) ^: (в - w#)

Появившийся тензор третьего ранга обозначим

A = 5 ( e₁e₁e₂ + e^^ - e₂eiei + e₂e₂e₂ )

(15) , тогда для атомов из одной подрешетки получим

r * - r - = F ■ ( R k - R - )

Для атомов из разных подрешеток с межатомным расстоянием a rk - r, = F ■ (Rk - R-) + a A: £ .

Тензор третьего ранга Δ содержит дополнительный параметр материала δ, который также определяется в рамках подхода атомарной статики. Внутренние смещения при учете малости искажений решетки вычисляются по формулам

Уф^8,1 n n

_                Г ¹ 15 1 = 0, y= 0

51 —         I            52

1      Ф««              2

^Y5 1⁵1 18,= 0, y= 0

,

( X- 1) ф;\|           + ( х₂- 1) ф" I

X ¹       7't'^X₁ ⁵ 2 |g ₂ =0, X , =1, X ₂ =1          ^{2        ,Гх} 2 ° 2 |g ₂ =0, X , =1, X ₂ =1

ф:8

^{T 5} 2 ⁵ 2 ls ₂ =0, X 1 =1 X ₂ =1

.

Прямые расчеты методом атомарной статики показали, что величина δ в (15) зависит от выбора параметров потенциала m и n и числа атомов на стороне образца N (рис. 2, б). Предельные значения равны следующим величинам:

• 1)    m=6, n=5: δ ^∞=0,064

• 2)    m=5, n=3: δ ^∞=0,091

Поскольку потенциальная энергия графена зависит от внутренних смещений δ, то при малых искажений кристаллической решетки графена и малых внутренних смещений, упругая энергия содержит слагаемое 2 8 • c • 8:

u = 1(F -1 - w#): C :(F -1 - w#) + 1 6 • c • 8 , где c – тензор второго ранга. Для графена это шаровой тензор c= cI:

u = 1 ( F - 1 - w„ ): C : ( F - 1 - w„ ) + 1 c 8 • 8 2               #                      #2

.

Используя связь (14), вектор внутренних смещений    можно    представить    в    виде

8 = A: (F -1 - w#), где тензор А определяется выражением (15), тогда u = 1 (F -1 - w„ ): C: (F -1 - w„ ) +1 c (F -1 - w„ ): Л: (F -1 - w„ )

, где тензор

Л - 5 ² ( e₁e₂e₁e₂ + e₂e₁e₂e₁ - e^e^ + e₂e₂e₂e₂ ) . Окончательно получим:

u = 1 ( F - 1 - w_# ): ( C + c Л ): ( F - 1 - w_# ) .

В натурных экспериментах, как и в динамических расчетах, определяются компоненты тензора C + c Λ . В статических методах без учета внутренних смещений определяется только C , что является одной из причин расхождения экспериментальных и расчетных значений в статических подходах.

Вычисленные с помощью поправок от учета внутренних смещений, значения коэффициента Пуассона ν для образцов различного размера при значениях m и n (п ара метров потен циала Ми) из множеств n = 3,8, m = n + 1,14 принадлежат интервалу v e (0.1; 0.99) . Лучшее приближение к значению _v = 0.17 ± 0.01 , определенному экспериментально для графита [3] получено при

б)

Рис. 2. Зависимости от числа атомов N образца для двух наборов m и n: а) безразмерного межатомного расстояния a / а , б) безразмерного параметра δ внутренних смещений. Пунктирные линии – горизонтальные асимптоты

Поскольку параметр α уже определен для различных значений m и n , то по экспериментальному значению модуля Юнга можно идентифицировать параметр β . «Двумерный модуль» Юнга равен E ² D « 340 ± 50 (Н м^-1), тогда

• 1)    m=6, n=5: β=2,41x10^-22 (Дж)

• 2)    m=5, n=3: β=1,15x10^-22 (Дж)

а)

Одо С? ИЗ

б)

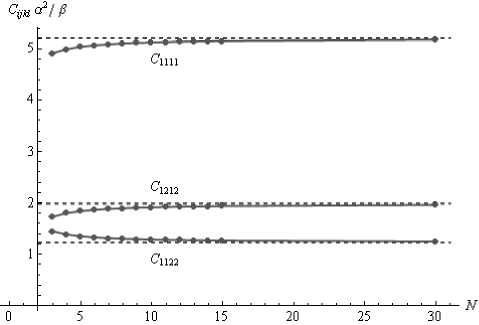
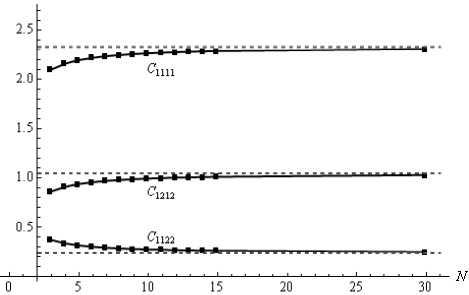
Рис. 3. Зависимость безразмерных упругих модулей от числа атомов N на стороне образца: а) при m =6, n =5, б) при m =5, n =3

Полученные два набора параметров потенциала Ми дают одинаковые значения модуля Юнга и межатомного расстояния для монослоя графена, точно совпадающие с экспериментальными значениями (табл. 3). Различие остается в коэффициенте Пуассона, который в известных экспериментах был получен не для листа графена, а для образца графита и требует уточнения. Найденные параметры потенциала Ми позволяют исследовать механические свойства графита или структур на основе графена в статической постановке.

Таблица 3. Экспериментальные значения

E 2D (Па - м)	V	a (нм)	Способ получения
345	0,236	0,142	Расчет при значениях параметров потенциала Ми: m = 6 , n = 5 , а = 1.29 х 10 - 10(М), Р = 2.41 Х 10 - 22 (Дж)
345	0,17 ± 0,01	—	Эксперимент Blakslee O.L., 1970 [3]
345	0,102	0,142	Расчет при значениях параметров потенциала Ми: m = 5 , n = 3 , а = 1.30 Х 10 - 10 (м), Р = 1.15 х 10 - 22 (Дж)
365	0,125	0,142	Эксперимент Bosak A., 2007 [8]

Выводы: показано, что применение даже самых простых потенциалов межатомного взаимодействия, когда направленность ковалентной связи учитывается алгоритмически за счет выборочного описания притяжения между атомами, позволяет достаточно точно прогнозировать упругие свойства графена. Близкие к экспериментальным значениям оценки упругих модулей получены благодаря учету внутренних смещений, а также идентификации безразмерных параметров потенциала по коэффициенту Пуассона. Полученная при низкой температуре симметрия тензора линейно-упругих свойств объясняется идеальной структурой исследуемой решетки графена. При наличии дефектов или при нагреве образца возможно нарушение симметрии решетки и появление несимметрии упругого отклика. Также при нагреве происходит увеличение коэффициента Пуассона графена, что позволит получить при некоторой ненулевой температуре еще лучшее приближение коэффициента Пуассона к экспериментальному значению.

Работа выполнена в рамках задания № 2014/152 на выполнение государственных работ в сфере научной деятельности в рамках базовой части госзадания Минобрнауки РФ (код проекта — 1911) .