Влияние выбора распределения точек изображения графем на распознавание символов методом сравнения форм

Одним из актуальных направлений исследований в области компьютерного зрения является распознавание рукописных документов. Существует множество решенных практических задач, например распознавание записей на почтовых отправлениях, банковских чеках, распознавание протоколов о происшествиях [1], [2]. Одной из востребованных задач является распознавание стенографических документов. Ее решение вызывает определенные сложности. Во-первых, в России в архивах находится большое число стенографических документов XIX века, которые не были расшифрованы, а специалистов, владеющих знаниями о существовавших стенографических системах, нет. Наличие расшифрованных документов позволяет с помощью системы распознавания автоматизировать процесс дальнейшей расшифровки стенограмм. Во-вторых, часто качество документов недостаточно высокое. Встречаются повреждение бумаги, выцветание записей, исправления текста, заваливание строк [3]. Все это создает проблемы при обработке изображений и влияет на точность распознавания.

РАСПОЗНАВАНИЕ СИМВОЛОВ

В рамках работы были проведены следующие этапы [4]:

• •    сегментация символов стенограмм;

• •    бинаризация символов;

• •    очистка от шумов и мусора.

Пример обработки символов показан на рис. 1. В результате обработки была получена коллек-

ция более чем из 5000 изображений стенографических символов. Для исследования влияния распределения выбранных точек изображения на качество работы методом сравнения форм была подготовлена контрольная выборка из 300 символов.

В качестве основного метода сравнения стенографических символов нами был выбран метод сравнения форм [5], [6]. Метод основан на определении положения точек изображения относительно друг друга. Количество точек сравниваемых изображений должно быть одинаковым. Обозначим множество точек за N. Выбор точек изображения осуществляется по заданным правилам из множества D. В зависимости от выбора множества точек результат распознавания может измениться, так как оно определяет геометрическую структуру символа.

После выбора для каждой точки пространство вокруг нее делится на зоны (назовем их корзинками), как показано на рис. 2с. Оставшиеся точки, число которых N-1, распределяются по корзинкам. Примем число корзинок равным K.

Рис. 1. Фрагмент стенограммы и обработанные символы

В результате для каждого изображения мы получаем массив значений размерности N*K.

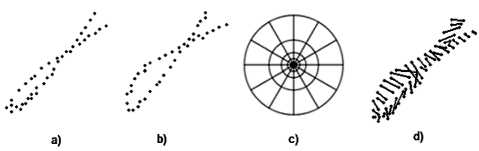
Рис. 2. Метод сравнения форм: а) и b) – точки сравниваемых изображений; с) границы корзинок; d) связанные точки

За меру сходства изображений примем суммарное смещение N точек одного изображения относительно N точек другого. Точки изображений сопоставляются с помощью решения задачи назначений (рис. 2d). Стоимость соединения точек мы определяем на основании распределения точек по корзинкам с помощью критерия X2.

K

C . , , = C ( p. . q , ) = т- 2 ² k = 1

[ h ( ^k )^- h j ^{( k} ) ] ² h ( ^k ) + h j ^{( k} ) ,

hi(k) – число точек в k-й корзинке для i-й точки, где i = 1..N; k = 1..K.

В качестве исходных данных задачи назначений мы получаем матрицу C со значениями cij, где i,j = 1..N. Задача назначений решается венгерским методом.

H⁽ⁿ ) = 2 C ⁽ p i , q _m (A ).

2 C ( p i , q n «И min.

В результате мы получаем сопоставление выбранных N точек двух изображений. За меру сходства принимается суммарное Евклидово расстояние между этими точками.

Рассмотрим различные варианты выбора точек.

Bыбор точек с использованием равномерной случайной величины . Используем генератор случайных величин с дискретным равномерным распределением. На каждом шаге мы получаем номер точки и извлекаем точку из множества D. В итоге на n шаге получаем множество выбранных точек N. Данный алгоритм не требует большого числа вычислений, но качество распределения точек низкое.

Bыбор точек с использованием правил для обеспечения визуально равномерного распределения точек на плоскости. Используем генератор случайных величин с дискретным равномерным распределением и правило позиционирования точек. Первый этап заключается в определении максимального расстояния между любыми двумя точками изображения. Максимальное расстояние, деленное на 10, будет контрольным расстоянием. Следующий этап предполагает последовательный выбор случайных точек. На каждом шаге выбирается точка, ко- торая проходит проверку. Расстояние от данной точки до любой ранее выбранной точки должно превышать контрольное расстояние. Если точка проходит проверку, то она извлекается из множества D во множество N. Если оставшиеся в D точки не проходят проверку позиционирования, а необходимое число точек во множестве N не достигнуто, то уменьшается контрольное расстояние. В результате полученное множество N содержит максимально удаленные друг от друга точки. Данный алгоритм требует большее число вычислений, чем первый, что связано с проверкой правил и многократным обходом множества D. При этом полученные результаты равномерно распределены на плоскости изображения символа.

Bыбор точек с использованием структурных аспектов их расположения в символе. Первый этап. Выбор точек осуществляется на основе их схожести по расположению в символе. Для каждой точки изображения мы строим множество корзинок и подсчитываем вхождения остальных точек в них. Обозначим число корзинок для каждой точки K. В результате мы получаем D множеств К. Следующий этап заключается в вычислении расстояния X² между всеми точками изображения. Полученные расстояния сортируются в порядке убывания. Обозначим множество расстояний X. На третьем этапе осуществляется выбор точек. Первая пара точек с самым большим расстоянием является исходной и имеет наиболее различные структурные показатели. Последующие пары выбираются из упорядоченного списка расстояний в порядке убывания. Важным фактором является проверка схожести структурных признаков не только самой пары, но и соотношения точек пары с ранее выбранными точками. Пусть ij – текущая пара для выбора. Тогда рассматриваем выбор точки i. Расстояние R_i j между точками i и j берем как эталон на данном шаге. Далее определяем расстояние от точки i до каждой точки из множества N.

R, = min R .

i p = 1.. N ip

Если Ri меньше, чем эталонное Rij, то точка не выбирается. Проверка точки j происходит аналогично. Выбор пары точек и их проверка происходит до наполнения множества N необходимым числом точек. Данный метод требует большого числа вычислений. При этом он учитывает структурные особенности написания символа, например толщину линий. Распределение точек получается визуально равномерным на плоскости.

СРАBНЕНИЕ РЕЗУЛЬТАТОB РАСПОЗНАBАНИЯ B ЗАBИСИМОСТИ ОТ BЫБОРА РАСПРЕДЕЛЕНИЯ ТОЧЕК

На рис. 3 приведены изображения распределения точек для каждого из перечисленных методов.

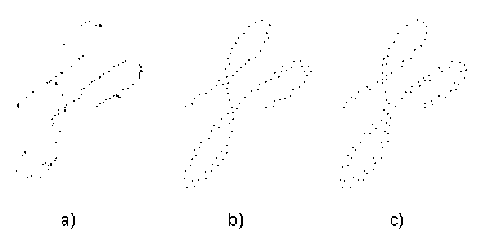
Рис. 3. Пример распределения точек

строка содержит результаты работы метода сравнения форм с выбором точек с использованием структурных аспектов их расположения в символе.

Результаты работы метода сравнения форм

	Точность	Полнота	F-мера
1	41 %	89 %	0,561
2	54 %	93 %	0,684
3	54 %	95 %	0,688

Результаты работы метода сравнения форм с различными распределениями точек на контрольной выборке приведены в таблице. Первая строка соответствует выбору точек с использованием равномерной случайной величины. Вторая – выбору точек с использованием правил для обеспечения визуально равномерного распределения точек на плоскости. Последняя

Наилучший результат показал выбор точек с использованием структурных аспектов их расположения в символе. Данный метод имеет большую вычислительную сложность на этапе подготовки, но современные технологии, такие как распределенные вычисления и облачные технологии, позволяют достичь приемлемого времени обработки символов.

* Работа выполняется при финансовой поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.

Shterkel ’ I. A. , Petrozavodsk State University (Petrozavodsk, Russian Federation)

THE INFLUENCE OF GRAPHEME IMAGE DOTS’ DISTRIBUTION ON SYMBOL RECOGNITION

BY THE SHAPE MATCHING METHOD