Влияние высоты фермы на область безопасных частот статически определяемой плоской фермы

• 1    Введение / Introductions

В динамике конструкций при строительстве и монтаже ферменных конструкций наибольший интерес вызывают два вопроса: первая собственная частота и спектр собственных частот фермы. Для решения задач о собственных частотах колебаний фермы обычно используют численные методы, основанные на методе конечных элементов. Фермы с небольшим количеством панелей реже встречаются на практике, чем масштабные фермы с большим числом панелей. В последнем случае любые численные методы проявляют свой недостаток — неизбежное накопление ошибок. Применение аналитического метода к статически определенным фермам с произвольным числом панелей решает эту проблему. Некоторые аналитические решения для прогибов плоских ферм в системе Maple представлены в [1]–[4]. Обычно для динамических расчетов интерес представляет верхняя или нижняя оценка первой частоты. Полезными методами являются метод Донкерлея (для нижней оценки) [5]–[7] или метод Рэлея (для верхней оценки) [8], [9]. Метод Донкерлея удобен тем, что в отличие от метода Рэлея он проще и не требует прогнозирования формы колебаний. Однако точность этого метода не очень высока. В некоторых случаях, когда ферменная конструкция сложна, точность этого метода с увеличением числа панелей не уменьшается или является неудовлетворительной. Напротив, метод Рэлея часто дает результаты с более высокой точностью. Однако коэффициенты, полученные этим методом, обычно бывают достаточно сложными и во Luong, C.L.; Kirsanov, M.

Effect of truss height on the safe frequency region of a statically determined flat truss;

многих случаях найти решение коэффициентов формулы расчета невозможно. В данном исследовании для определения первой собственной частоты фермы используется метод Донкерлея и его упрощенная форма [10]. Усовершенствованные варианты метода Донкерлея рассмотрены в [11], [12]. Коэффициенты, полученные этим методом, столь же просты, как и метод Донкерлея, и почти столь же точны, как и метод Рэлея.

Компьютерные программы, использующие символьную математику со специальными операторами, такие как Maple, могут использоваться для символьного решения систем линейных уравнений [13]–[16]. Решение для оценки собственных частот в аналитическом виде с использованием системы компьютерной математики Maple было получено в [17]. Вопросы существования статически определимых ферменных систем впервые обсуждались в работах Hutchinson R.G. and Fleck N.A. [18], [19]. Расчет оптимальных размеров обычной фермы с учетом ползучести приведен в [20]. Нелинейная параметрическая вибрация пластин переменной толщины изучалась в [21].

• 2    Материалы и методы / Materials and Methods

  2.1    Конструкция фермы

Рассматриваемая ферма представляет собой статически определенную плоскую симметричную ферму (рис. 1). ферма имеет одну подвижную и одну неподвижную шарнирную опору. Длина фермы L = 4 an . Вся масса фермы условно распределена по N = 8 n + 6 узлам конструкции, за исключением двух опорных узлов. Ферма содержит v = 16 n + 6 стержней. В это число также входят три стержня, моделирующие опоры.

Рис. 1 - Ферма, n = 4

Fig. 1 - Truss, n = 4

Координаты узлов и структура соединение стержней в ферме определяются в программе символьного математического языка Maple. На рисунке 2 показана нумерация стержней и узлов фермы на примере фермы n = 2 .

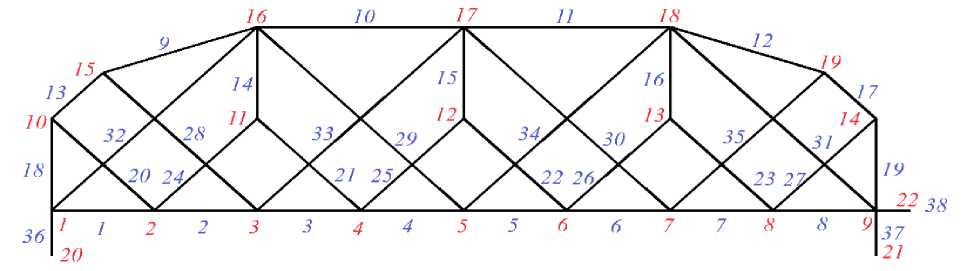
Рис. 2 - Нумерация стержней и узлов, n = 2

Fig. 2 - Numbering of bars and nodes, n = 2

2.2    Собственная частота колебаний

Нижняя оценка частоты первого колебания по формуле Донкерлея выражается следующим образом:

K

<=z® - ² ,

i =1

где Ю p — парциальные частоты, рассчитанные для каждой массы отдельно, K = 8 n + 3 — число степеней свободы системы грузов в узлах фермы.

Для расчета парциальных частот составляются уравнения движения масс M , размещенных в узлах:

M y _p + D_py_p = 0, p = 1,2,..., K .

Коэффициент жесткости D_p , обратный к коэффициенту податливости, вычисляется по формуле Максвелла – Мора:

a p = 1/ D p = £ ( S a ) ² 1 a /( EF ).

a= 1

Из формулы Донкерлея при y p = A p sin( w t + ф ) следует: o p = D p / IM . Отсюда получается выражение для частоты по Донкерлею:

K o- = M £ 8V = MA„. pn

p = 1

Расчет серии ферм с разным числом панелей показал, что коэффициент Д _n имеет вид, не зависящий от параметра n :

_Д = (532 a ³ + 1335 c ³ + 17 d ³ + 1104 h ³)

^Д 2

(6334 a ³ + 10705 c ³ + 89 d ³ + 5488 h ³)

Д 3

(94956 a ³ + 59951 c ³ + 337 d ³ + 22672 h ³)

Д 4

(699350 a ³ + 230106 c ³ + 889 d ³ + 70576 h ³)

(15982836 a ³ + 3584419 c ³ + 9365 d ³ + 876560 h ³)

С помощью системных операторов Maple вычисляются общие члены полученной последовательности коэффициентов при степенях размеров фермы: a , c , h . Здесь обозначены длины раскосов: c = ya2 + h2 , d = 9aa2 + h2 • Из формулы следует, что зависимость прогиба от числа панелей и размеров конструкции имеет вид:

Д _n = ( C 1 a ³ + C ₂ c ³ + C 3 d ³ + C 4 h ³) I ( h ² EF ),

Коэффициенты в этом выражении получаются из решения рекуррентных уравнений в системе Maple:

C 1 = (5120 n ⁷

C 2 = (4096 nn

C 3 = ( 64 П

C 4 = ( 64 n

^^^^^^^^^в

—

• —    21504 n ⁶ +48896 n ⁵ — 72000 n ⁴ + 69680 n ³ — 29076 n ² + 4734 n +135) /360,

• —    36864 n ⁶ +194560 n ⁵ — 375360 n ⁴ + 370504 n ³ — 96816 n ² +1575 n —1620)/1440,

120 n ³ +128 n ² — 21 n )/ 96 ,

80 n ⁴ + 80 n ³ +182 n ² — 39 n )/ 6 .

Таким образом, формула для расчета первой частоты колебаний фермы будет иметь вид:

M D = h

EF

M(C1 a3 + C2c3 + C3d3 + C4h3) , где коэффициенты вычисляются по формулам (6).

2.3    Упрощенный метод оценки первой частоты

Приближенная оценка первой частоты колебаний по упрощенному методу имеет следующий вид:

K ft*2 = Z up.                                                (8)

p = 1

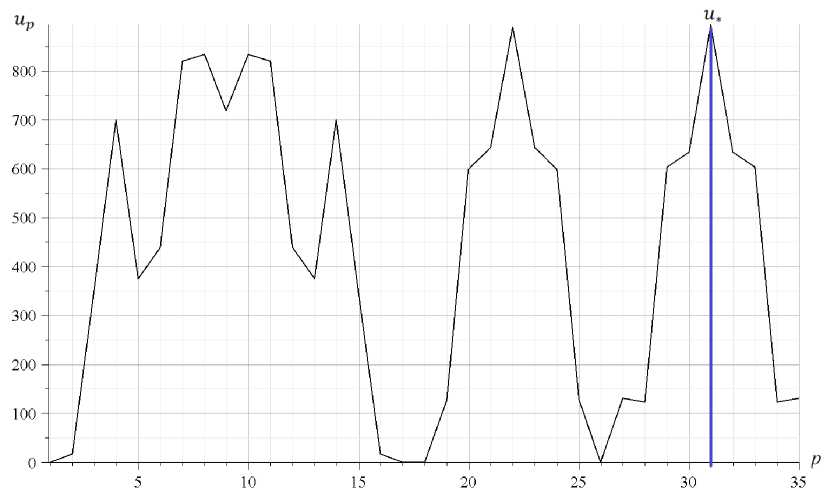
Рис. 3 - Зависимость коэффициента от номера узла фермы при n = 4

Fig. 3 - Dependence of the coefficient on the truss node number at n = 4

Приняты размеры фермы: a = 6м, h = 6м. Продольная жесткость стальных стержней сечением F = 4 • 10—4м2 равна EF = 0,8 ■ 105 кН, число степеней свободы K = 8n + 3 = 35 . На оси абсцисс K отложены номера узлов. Максимальная ордината обозначена и* . Сумму ZиР можно p=1

интерпретировать как площадь, ограниченную кривой распределения. Эту площадь можно вычислить проще, отсортировав частоты в порядке возрастания и рассчитав площадь по формуле площади

K трапеции ^up = K (u* + u1)/2 (рис. 4). где u*, u1 — максимальный и минимальный прогиб некоторого p=1

узла фермы от действия единичной силы.

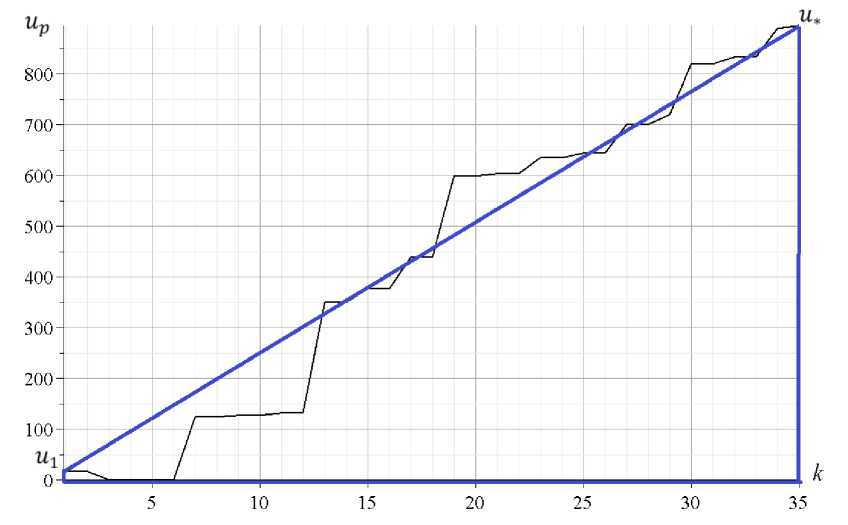
Рис. 4 - Коэффициенты u p в порядке возрастания при, n = ⁴

Fig. 4 - Coefficients u p in ascending order at ^{n = 4}

При этом трапеция оказывается вписанно-описанной фигурой исходной площади, что делает такую замену оправданной. В этом случае на рисунке 4 на оси абсцисс уже отмечены не номера узлов, а номера ранжированного по увеличению списка значений и * . Пробные вычисления величины й * при различных n показывают, что максимальное значение й * приходится на средний узел верхнего пояса фермы, имеющий номер 7 n + 3 . Вычисление величины й * = и - _{n + 3} для различных порядков фермы дает следующую последовательность:

n = 1: u *

n = 2 : u *

n = 3 : u *

n = 4 : u *

n = 5 : u *

n = 6 : u *

11 a ³ + 11 c³

2 h ² EF ^,

1672 a ³ + 2717 c ³ + 19 d ³ + 1520 h³

8h2EF

513 a ³ + 81 c³

2h2EF

31360 a ³ + 4193 c ³ + 7 d ³ + 1008 h³

40h2EF

3655 a ³ + 215 c³

2h2EF

800360 a ³ + 32079 c ³ + 17 d ³ + 3536 h³

216 h ² EF

Вычисления прогиба производятся последовательно с n = 1,2,3... . Обобщение этой серии формул на произвольное число n дает следующие окончательные формулы:

C 1 = (64 n ⁷ -168 n ⁶ - 8(2(-1) ⁿ -11) n ⁵ + 6(11(-1) ⁿ + 6) n ⁴ + (67(-1) ⁿ +103) n ³ -

- (33(-1) ⁿ + 6) n ² -18((-1) ⁿ +1) n ) / 6,

C ₂ = (128(5 - (-1) ⁿ ) n ⁵ + 48(11(-1) ⁿ - 31) n ⁴ + 8(139(-1) ⁿ + 247) n ³ +

+ 72(7(-1) ⁿ +16) n ² + 63((-1) ⁿ +1) n ) / 48,

C 3 = n ( 8 n + 3 ) ((-1) ⁿ +1) / 16 ,

C ₄ = n ( 16 n ² +14 n + 3)((-1) ⁿ +1) .

Для обобщения используются операторы Maple rsolve и rgf_findrecur. Формула зависимости первой частоты собственных колебаний фермы, полученная с помощью упрощенного метода, принимает вид:

ro * = h

EF

M ( C 1 a ³ + C 2 c ³ + C 3 d ³ + C 4 h ³ )^.

• 3    Результаты и их обсуждение / Results and Discussion

Полученные оценки зависимости частоты собственных колебаний от порядка фермы необходимо сравнить с минимальным значением всего спектра частот, полученным численным методом. В качестве примера рассмотрим регулярные фермы из стали с модулем упругости E = 2 - 10⁵ МПа, с площадью поперечного сечения стержней F = 4см² . Массы в узлах M = 150кг , размеры a = 6 м , h = 6 м . На рисунке 5 кривая ш 1 соответствуют численному решению, полученному как минимальная собственная частота спектра, кривая ш D построена по формуле (7) с коэффициентами, найденными по методу Донкерлея, кривая ш * , построена по упрощенной формуле (9).

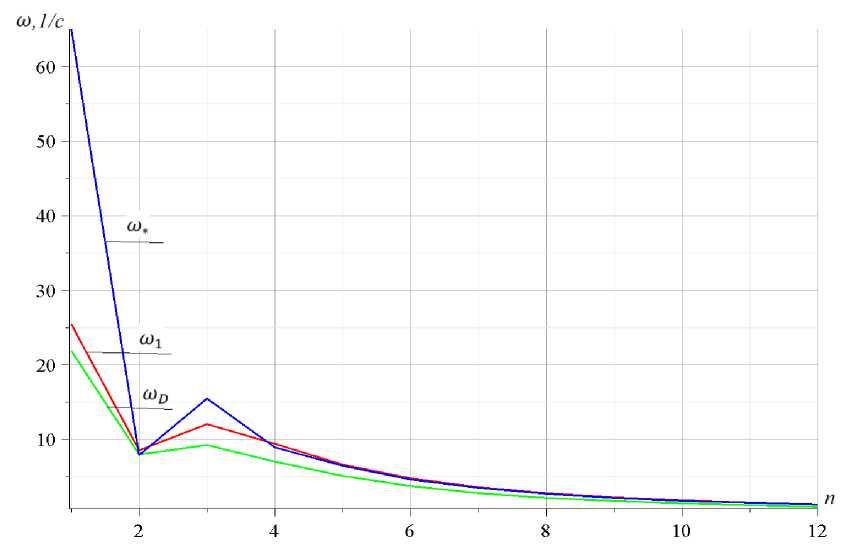
Рис. 5 – Зависимость первой частот от числа панелей фермы

Fig. 5 – Dependence of the first frequency on the number of truss panels

Из рисунка 5 видно, что при количестве панелей n <  4 наименьшее значение частоты численного метода и аналитического метода сильно различаются. Однако это несущественно для практики, так как стропильных конструкций с таким небольшим количеством панелей не существует. При n >  4 видно, что результаты, полученные методом Донкерлея, упрощенным методом и численным методом, практически совпадают. С увеличением числа панелей первая собственная частота монотонно уменьшается. Отсюда можно сделать вывод, что аналитическое решение, полученное методом Донкерлея и упрощенным методом, подходят для решения ферменной задачи с большим количеством панелей.

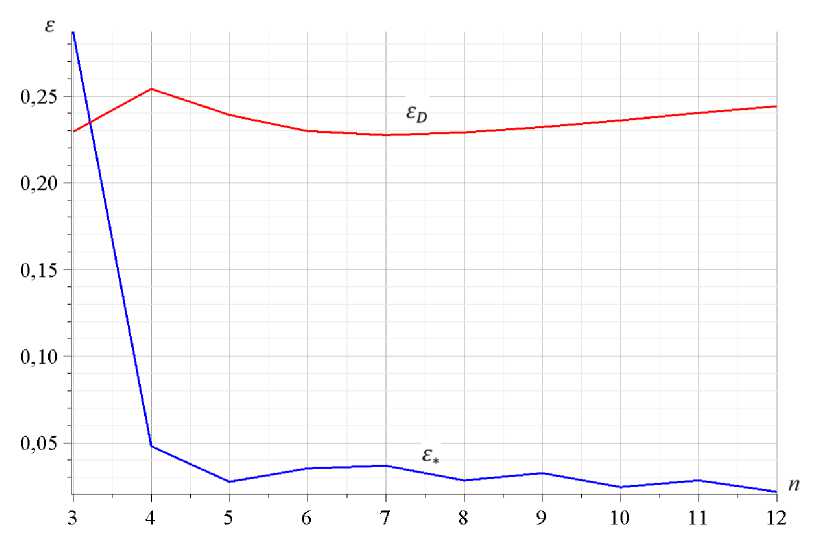
Рис. 6 - Относительные погрешности методов a = 6 м , h = 6 м .

Fig. 6 - Relative errors of methods a = 6 м , h = 6 м .

Для более точной оценки полученных решений применяются безразмерные значения относительных погрешностей £ D = ( o 1 - го D )/ o 1 и s * = ( o 1 - o * )/ o 1 . Из рисунка 6 видно, что для метода Донкерлея погрешность находится в пределах допустимого диапазона от 22 до 25%. Но с увеличением количества панелей погрешность метода Донкерлея также несколько увеличивается. Это не совсем подходит для ферм с большим количеством панелей. Напротив, упрощенный метод показывает очень хорошие результаты. При малых значениях n по мере увеличения числа панелей погрешность этого метода очень быстро уменьшается. При n >  4 погрешность, полученная упрощенным методом, всегда меньше 4% и стабильно уменьшается с увеличением числа панелей. Величина погрешности достигает 0.5% при n = 12 . Отсюда можно сделать вывод, что для рассматриваемой фермы упрощенный метод дает лучшие результаты и больше подходит для ферм с большим числом панелей. Кроме того, для упрощенного метода можно выделить еще одно свойство: точность этого метода наибольшая, когда число панелей n нечетное.

3.1    Спектры собственных частот регулярных ферм

На графике (рис. 7) показаны спектры двенадцати регулярных ферм в порядке n = 1,...,12 . Используя математический аппарат, используемый для нахождения первой частоты в режиме численного расчета, на графике показывает распределение частот ферм в разных порядках. Это позволяет определить некоторые свойства распределения спектральных множеств. Каждая кривая соответствует ферме определенного порядка. Ординаты точек на ней — это частоты. Горизонтальная ось представляет номера собственных частот в упорядоченном спектре.

1/с

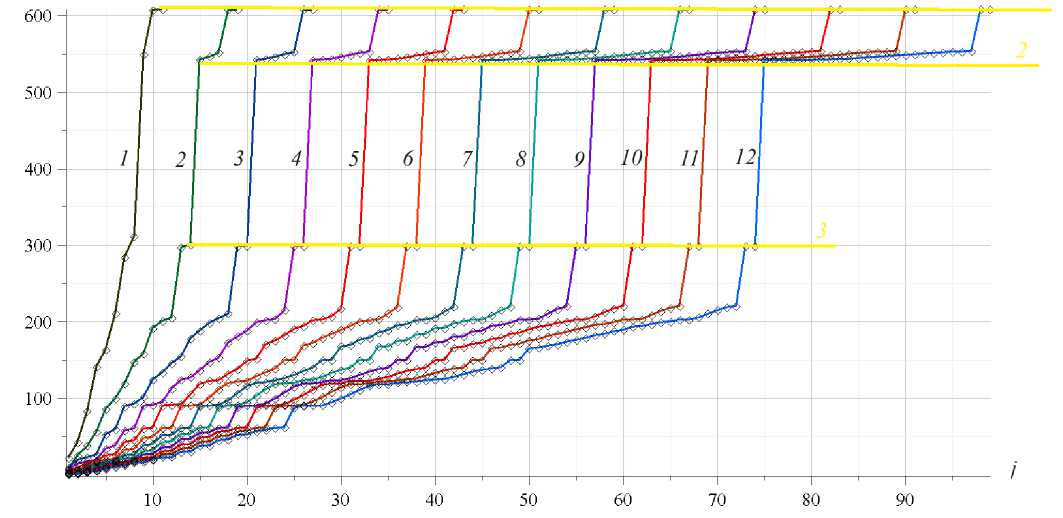
Рис. 7 - Спектры регулярных ферм a = 6 м , h = 4 м .

Fig. 7 - Spectra of regular trusses a = 6 м , h = 4 м .

Здесь приняты размеры фермы a = 6 м , h = 4 м . Наиболее заметными являются три горизонтальных отрезка, соединяющих точки, изображающие значения собственных частот. Это спектральные константы, обозначаемые цифрами 1, 2, 3. Верхняя граница частоты 1 принадлежит всем спектрам фермы. Наличие этих констант позволяет с высокой точностью прогнозировать Luong, C.L.; Kirsanov, M.

Effect of truss height on the safe frequency region of a statically determined flat truss;

частоты крупномасштабных ферм с большим числом панелей на основе расчетных данных для фермы с малым числом панелей.

Размеры фермы не сильно влияют на общий характер картины распределения частот. Для ферм размером a = 6 м , h = 6 м собственные частоты показаны на рисунке 8.

w 1/с

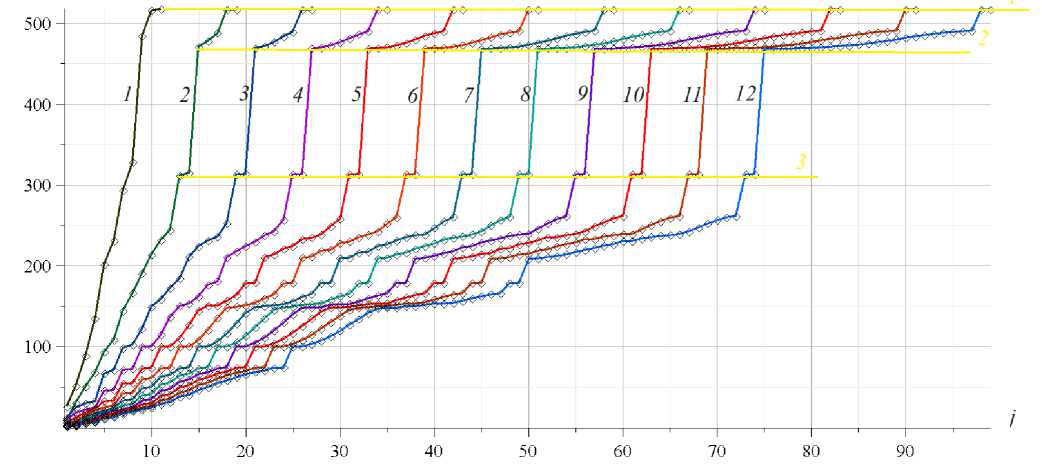
Рис. 8 - Спектры регулярных ферм a = 6 м , h = 6 м .

Fig. 8 - Spectra of regular trusses a = 6 м , h = 6 м .

3.2    Зависимость безопасного диапазона частоты от высоты фермы

Картины распределения частот ферм разного порядка обнаруживают области, в которых не собственных частот конструкции. Если внешнее возбуждение имеет частоту из этих областей, то резонанса от этого возбуждения не произойдет. Такие области будем называть резонансно безопасными.

При размерах a = 6 м , h = 6 м на рисунке 8 собственные частоты также имеют три константы. Интервал частот между константами 2 и 3 равен 150 c ^—1 . Между тем на рисунке 7 эта величина равна 250 c "1 . Значение частоты между этими двумя константами зависит от высоты h . На рисунке 9 показана зависимость размера резонансно безопасного диапазона от размера h . Горизонтальная ось представляет значение h , вертикальная ось — значение частоты между константами 2 и 3.

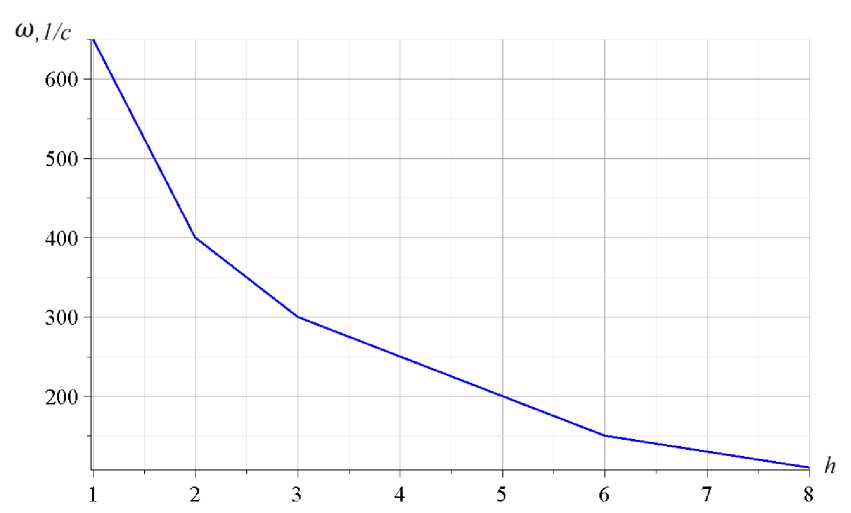
Рис. 9 – Зависимость безопасного диапазона частоты от h

Fig. 9 – Dependence of the safe frequency range on h

С увеличением высоты фермы размер зоны безопасности уменьшается.

• 4    Выводы/ Conclusions

Разработана математическая модель конструкции статически определенной плоской фермы и метод расчета первой частоты ее собственных колебаний в аналитическом виде для произвольного числа панелей. Нижние оценки частот собственных колебаний были получены с использованием метода Донкерлея и упрощенного метода. Формулы, полученные аналитическим методом, сравниваются с численным решением. Аналитическое решение лучше всего подходит для ферм с большим количеством панелей.

Можно сделать следующие выводы:

• 1.    Оценка наименьшей частоты, полученная упрощенным методом компактнее и одновременно значительно точнее оценки по методу Донкерлея. В рассматриваемой ферме погрешность упрощенного решения меньше 0.8 % при числе панелей n >  12 .

• 2.    С увеличением числа панелей первая частота колебаний фермы монотонно уменьшается. В спектре собственных частот регулярных ферм разных порядков замечены спектральные константы.

• 3.    Численно найдена зависимость резонансно безопасного диапазона от высоты фермы.