Влияние замены неаналитических траекторий с точками излома гладкими траекториями на сложность процессов деформирования и нагружения материалов
Автор: Зубчанинов В.Г., Алексеев А.А., Гультяев В.И.
Статья в выпуске: 2, 2020 года.
Бесплатный доступ
Данная работа посвящена экспериментальному исследованию влияния замены скруглениями угловых точек двузвенных ломаных траекторий деформирования при отображении процессов сложного нагружения при упругопластическом деформировании материалов. Замена угловых точек в их окрестности локальными участками окружностей позволяет неаналитическую траекторию заменить гладкой траекторией. Экспериментальные исследования выполнены на тонкостенных трубчатых образцах из материала сталь 3 на автоматизированном расчетно-экспериментальном комплексе СН-ЭВМ. Программы нагружения трубчатых образцов задавались в девиаторном пространстве деформаций А.А. Ильюшина. Рассмотрено скругление точки излома двузвенной траектории с ортогональным изломом дугами окружностей с кривизнами 200, 400, а также скругление точки излома двузвенной траектории с углом излома 135° дугами с кривизнами 400, 800. Представлены экспериментальные диаграммы, характеризующие векторные и скалярные свойства материала. Показано, что влияние сложного нагружения на зависимость между напряжениями и деформациями при переходе на криволинейный участок проявляется не сразу. Для рассмотренного материала после точки начала скругления величина модуля вектора напряжений сначала возрастает, а затем с образованием «нырков» напряжений убывает. Точка минимума «нырка» находится на последующей прямолинейной части траектории деформирования. На участке скругления угол сближения возрастает, а на последующем прямолинейном участке - убывает и с ростом деформации стремится к нулю. Скорость уменьшения угла сближения мало зависит от различия в геометрии предшествующей траекторий деформирования. При деформировании по прямолинейному участку экспериментальные результаты для скругленных и нескругленных траекторий становятся мало отличимыми друг от друга. Таким образом, замена исходной неаналитической траектории на гладкую траекторию влияет на сложность процессов деформирования и нагружения материалов только в окрестности точки излома. Это обстоятельство можно учесть при численном моделировании процессов упругопластического деформирования материалов и интегрировании определяющих соотношений, заменяя неаналитические траектории гладкими.
Пластичность, эксперимент, сложное нагружение, тонкостенный трубчатый образец, векторные и скалярные свойства материалов, гладкая траектория, траектория деформирования, кривизна
Короткий адрес: https://sciup.org/146281993
IDR: 146281993 | УДК: 539.3 | DOI: 10.15593/perm.mech/2020.2.05
Текст научной статьи Влияние замены неаналитических траекторий с точками излома гладкими траекториями на сложность процессов деформирования и нагружения материалов
ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2020PNRPU MECHANICS BULLETIN
Экспериментальные исследования неупругого поведения материалов при непропорциональном нагружении и сложном напряженно-деформированном состоянии (НДС) являются критерием оценки достоверности и установления границ применимости отдельных определяющих соотношений теории пластичности. Одной из наиболее общих и развивающихся на сегодняшний день феноменологических теорий пластичности является теория упругопластических процессов, предложенная А.А. Ильюшиным [1, 2]. Развитие положений и гипотез теории, а также макроэкспериментальные исследования их достоверности представлены работами А.А. Ильюшина [3–5], В.С. Ленского [6–10], А.М. Жукова [11–14], Р.А. Васина [15–20], Дао Зуй Бика [21–23], В.В. Мос-квитина [24], В.П. Дегтярева [25–26], А.С. Кравчука [27–29], В.И. Малого [30–31], И. Охаши [32–37], Ю.Н. Шевченко [38–41], В.Г. Зубчанинова [42–51] и других исследователей [52–62].
Проведенные в этих работах экспериментальные исследования используют предложенное А.А. Ильюши- ным [1] векторное (геометрическое) представление процессов нагружения и деформирования в виде образа процесса нагружения или деформирования, включающего в себя траекторию, в каждой точке которой приписываются характеристики процесса: векторы напряжений, деформаций и их приращения, а также скалярные параметры (температура, средние напряжение и деформация и др.) В соответствии с постулатом изотропии А.А. Ильюшина [2–4] связь между напряжениями и деформациями в теории процессов определяется скалярными и векторными свойствами материалов. Например, для плоских траекторий деформирования произвольной кривизны эта связь представлена в виде определяющих соотношений [42]:
da t da i~
— = Mx pj +1 —- Mv cos9! I - , ds 1 1 I ds 1 1 )
d 9! , M . _ —1+ k, =--1sin 9,, ds 1 о 1
где s – длина дуги траектории деформирования;
- о - = S k i k , Э = Э Э = Э k i k ( k = 1,3) (2)
есть векторы напряжений и деформаций; ст , Э - их единичные векторы; ст , Э - модули векторов; р 1 = d Э / ds -единичный вектор, касательный к траектории деформирования в каждой ее точке;
S 1 = 3S S 11 = ^2 ( ст 11 ст 0 ), S 3 = 2S S 12
= V2 ст12,
Э 1
S 11
—
S o
) , Э 3 = 723 12
= 2S S12
есть координаты векторов ст и Э ; ст у , S j , S y , Э у ( i , j = 1, 2, 3) - компоненты тензоров и тензоров-девиаторов напряжений и деформаций; ст 0 = ст ii / 3, s 0 = s ii / 3 - средние напряжение и деформация; M 1 , d ст
– функционалы процесса, зависящие от параметров ds внутренней геометрии траектории деформирования: 0 длины ее дуги s, кривизны к и углов излома 91 ;
cos 9 1 = ст ■ р 1 ; 9 1 - угол сближения, который характеризует отклонение вектора σ от касательной к траектории деформирования в каждой ее точке и отражает влияние векторных свойств материала на процесс деформирования.
Постулат изотропии начально изотропных материалов описывает их векторные свойства при сложном деформировании по аналитическим траекториям. На практике процессы деформирования обычно реализуются по неаналитическим сложным траекториям, состоящим из ряда аналитических участков, границами которых являются точки их излома или точки смены кривизны. В этих точках в экспериментах наблюдаются нырки напряжений на диаграммах зависимостей между модулем напряжения и параметром прослеживания процесса s ( t ) [42–51].
При неаналитических траекториях возникает проблема разбиения траектории на ряд аналитических участков, что усложняет численные расчеты. Замена угловых точек в их окрестностях локальными участками окружностей позволяет неаналитическую траекторию заменить гладкой траекторией. Данная работа посвящена экспериментальному исследованию влияния такой замены при отображении процессов деформирования при сложном нагружении и упругопластическом деформировании материалов. Ранее подобные эксперименты были выполнены японскими исследователями под руководством И. Охаши [32, 33] на тонкостенных трубчатых образцах из малоуглеродистой стали S10C и латуни BsBM2. Ими были рассмотрены двузвенные траектории с прямым углом излома, скругленным дугой окружности. В данной статье представлены результаты опытов на тонкостенных трубчатых образцах из стали 3 для траекторий с углами излома 90° и 135°.
1. Методика и программы эксперимента
Испытания проведены на автоматизированном расчетно-экспериментальном комплексе на сложное нагружение СН-ЭВМ имени А.А. Ильюшина. Комплекс состоит из нагружающей установки, реализующей трехпараметрическое воздействие на образец (осевое растяжение-сжатие, кручение и внутреннее давление), датчиков усилий и деформаций, измерительных преобразователей сигналов датчиков, управляющей ЭВМ с программным комплексом и блока управления. В качестве модели, исследуемой на комплексе СН-ЭВМ, применяется тонкостенный трубчатый образец, в стенках которого при достаточно большом отношении радиуса срединной поверхности к толщине стенки реализуется однородное плоское напряженное состояние. Программы испытаний реализовывались в девиаторном пространстве деформаций 3 1 - Э3 (жесткое или кинематическое нагружение) при совместном действии на образцы осевой силы и крутящего момента. Процесс нагружения предполагался монотонным изотермическим, а деформации – малыми.
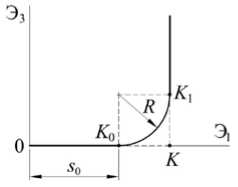
В первой серии опытов (рис. 1, а ) реализовывалась деформация по двузвенной ломаной траектории с прямым углом излома (образец 1 ) и скругление точки излома дугой окружности (образцы 2 , 3 ).
б
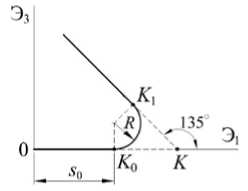
Рис. 1. Программы экспериментов при жестком нагружении на плоскости 3 1 - Э3: а - траектории с углом 90 ° , б - траектории с углом 135 °
Fig. 1. Strain trajectories on the plane Э 1 - Э3 : a - trajectories with angle 90 ° , b - trajectories with angle 135 °
Образец 1 после предварительной осевой деформации растяжения до s 0 = 2 % на первом прямолинейном участке, при изломе траектории в точке K на угол 9 0 = 90 ° на втором участке подвергался только дефор-
мации кручения по компоненте Э3 при Э 1 = const. Траектория деформации образца 2 имела скругление прямого угла по дуге окружности K 0 K 1 радиуса R = 0,25 % с кривизной к 1 = 400; длина первого участка s 0 = 1,75 % . Траектория деформации образца 3 при s 0 = 1,5 % имела скругление прямого угла по дуге окружности K 0 K 1 радиуса R = 0,5 % с кривизной к 1 = 200. После точки K 1 возрастала только деформация кручения Э3 при Э 1 = const.
Во второй серии опытов (рис. 1, б ) реализовывалась деформация по двузвенной ломаной траектории с углом излома 135 ° (образец 4) и аналогичное скругление точки излома дугой окружности (образцы 5, 6).
Образец 4 после предварительной осевой деформации растяжения до s 0 = 2 % на первом прямолинейном участке, при изломе траектории в точке K на угол 9 0 = 135 ° на втором участке подвергался совместному кручению по Э3 и сжатию по компоненте Э1 . Траектория деформации образца 5 при s 0 = 1,698 % имела скругление угла излома по дуге окружности K 0 K 1 радиуса R = 0,125% с кривизной к 1 = 800 при одновременном растяжении-сжатии по Э1 и кручении по Э3 до точки K 0 с координатами Э 1 = 1,787%, Э3 = 0,213% . У образца 6 траектория деформации при s 0 = 1,396% имела скругление угла излома по дуге окружности K 0 K 1 радиуса R = 0,25% с кривизной к 1 = 400 до точки K 0 с координатами Э 1 = 1,573%, Э3 = 0,427% .
Реализованные траектории со скруглением угла излома по терминологии А.А. Ильюшина являются гладкими, так как в местах перехода ее участков отсутствуют точки излома, но изменяется кривизна, т.е. у функций Э( s ) , описывающих траекторию в линейном пространстве, первые производные непрерывны, а вторые терпят разрыв.
В качестве образцов использовались цилиндрические тонкостенные оболочки из стали 3 в состоянии поставки, которые имели толщину стенки h = 1 мм, радиус срединной поверхности поперечного сечения r = 15,5 мм и длину рабочей части 1 = 110 мм. Начальная изотропия материала образцов с достаточной степенью точности подтвердилась в базовых опытах при простом нагружении (растяжение, сжатие и кручение). При обработке результатов экспериментальных данных для определения компонент тензоров деформаций b j и напряжений a j использовались формулы [42]
A 1 A r
S 11 = “Г, S 22 = , S 12
< 1 r
S 33 = (s 11 + S 22 ) + ,
K
r V п
= 2 1 ’ S13 = S 23 = 0,
S 0 = 3 (s 11 + S 22 + S 33 ) ,
P rM
-
a11 = ^"T, a22 = q7, a12 = .
2 n rh h 2 n r 2 h
-
• Q33 « О, CT13 = CT23 = 0,
an = -(a,j + a77 + a33), K =---—,
I 0 3V 11 22 33^ 3(1 -2ц)’ где A1 и Ar - приращения 1 иг ; v - угол поворота поперечного сечения; P - растягивающая осевая сила; q - внутреннее давление; M - крутящий момент; E -продольный модуль упругости; ц - коэффициент Пуассона; K - объемный модуль упругости. При обработке экспериментальных данных принималось условие несжимаемости (s0 = 0), достаточно точное вне упругой области, так как ц достаточно быстро стремился к значению 0,5. Координаты векторов деформаций и напряжений формоизменения определялись через компоненты тензоров по формулам (3). При обработке результатов экспериментальных исследований для определения угла сближения 91 вектора напряжений к касательной траектории деформирования для прямолинейных участков использовалось выражение cos 91 = [^1(Э1 - Э*) + 53 (Э3 - Э3)], (6)
aAsL J
где Э1* , Э*3 – значения Э 1 , Э 3 в начале каждого участка прямолинейной траектории. Для криволинейных участков
n 1 I С cos 9 1 = — 5 1 a I
(Э 3 - Э 3 ) R
-
S 3
(Э 1 - э 0 ) ) R J ,
где Э1 , Э3 - координаты центра окружности.
2. Экспериментальные результаты
На рис. 2–6 представлены результаты испытания трубчатых образцов по программам с углом 90 ° (см. рис. 1, а ).
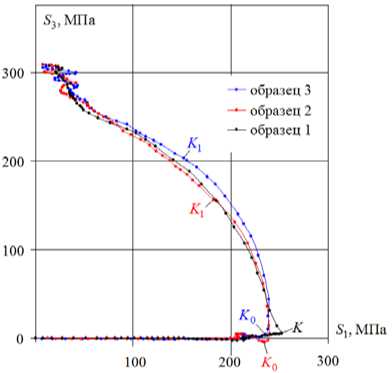
Рис. 2. Отклик по напряжениям на плоскости 5 1 - 5 3
Fig. 4. The chart characterizing vector material properties 91 - s
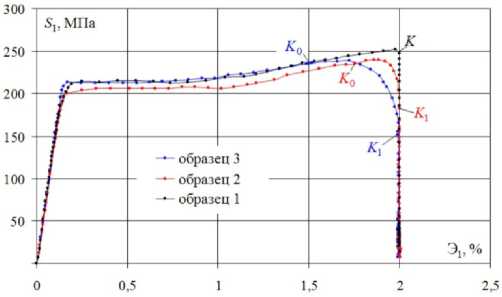
Рис. 5. Локальная диаграмма деформирования 5 1 - Э 1
-
Fig. 2. Stress response on the plane 5 1 - 5 3
На рис. 2 представлен отклик в пространстве напряжений 5 1 - 5 3 , на рис. 3 - диаграмма прослеживания процесса деформирования с- s , характеризующая скалярные свойства материала, а на рис. 4 – диаграмма зависимости угла сближения от длины дуги траектории деформирования 9 1 - s , характеризующая векторные свойства материала. На рис. 5, 6 приведены локальные диаграммы деформирования растяжения-сжатия по компонентам 5 1 - Э 1 и чистого сдвига по компонентам 5 3 - Э3.
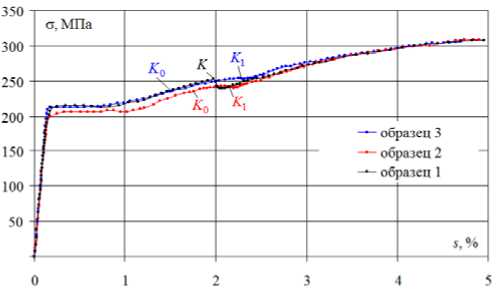
Рис. 3. Глобальная диаграмма деформирования с- s
-
Fig. 3. The global chart of deformation с - s
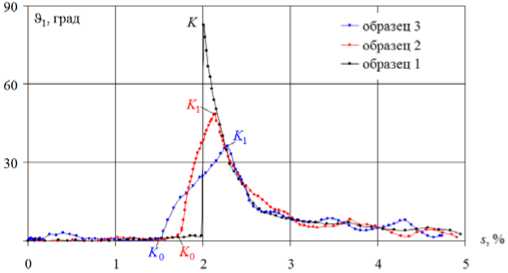
Рис. 4. Диаграмма характеристики векторных свойств материала 91 - s
Fig. 5. Local charts of deformation 5 1 - Э 1
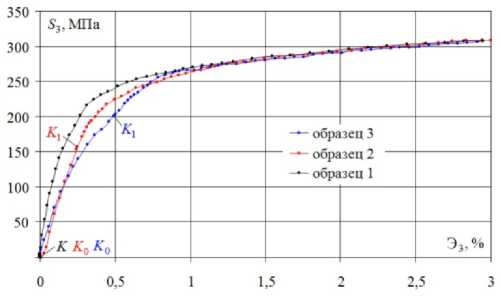
Рис. 6. Локальная диаграмма деформирования 5 3 - Э3
Fig. 6. Local charts of deformation 5 3 - Э3
Результаты испытания трубчатых образцов по программам с углом 135 ° (рис. 1, б) представлены на рис. 7–12.
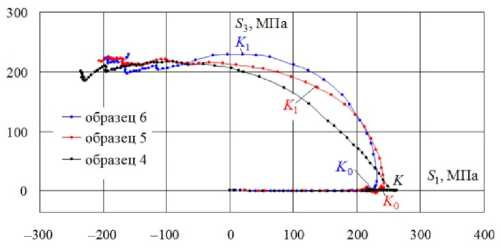
Рис. 7. Отклик по напряжениям на плоскости 5 1 - 5 3
Fig. 7. Stress response on the plane 5 1 - 5 3
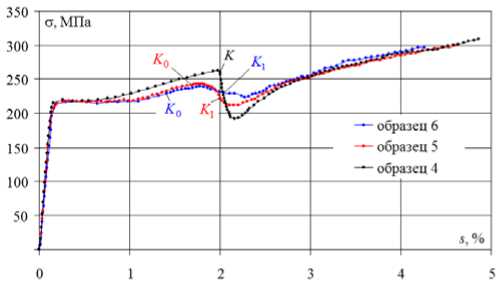
Рис. 8. Глобальная диаграмма деформирования а- 5
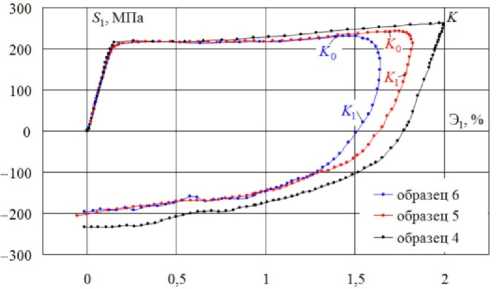
Рис. 11. Локальная диаграмма деформирования 5 1 - Э 1
Fig. 8. The global chart of deformation а - 5
Fig. 11. The local chart of deformation 5 1 - Э 1
Влияние кривизны при скруглении точки излома на траекториях с углом 90 ° существенно проявляется по векторным свойствам (см. рис. 4) и на локальных диаграммах (см. рис. 5, 6). На траекториях с углом 135 ° влияние кривизны существенно проявляется по скалярным (см. рис. 8, 9) и векторным свойствам (см. рис. 10). Также при скруглении точки излома наряду с прямым нырком напряжений на диаграмме а - 5 (см. рис. 8) образуется обратный нырок на диаграмме а - Э (см. рис. 9).
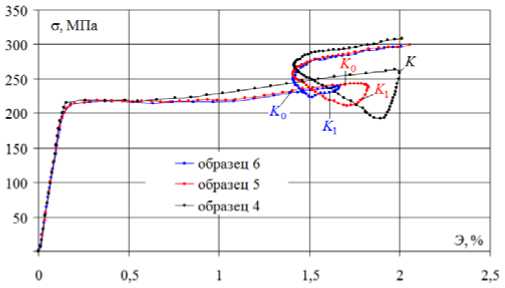
Рис. 9. Глобальная диаграмма деформирования а Э
Fig. 9. The global chart of deformation а - Э
Для оценки влияния кривизны траектории на величины нырков напряжений построены зависимости безразмерной величины а = а / а ^ , где а ^ - значение а в точке скругления K 0 (или излома K ), от приращения длины дуги траектории деформирования A s = 5 - 5 0 после начала скругления в точке K 0 (или излома K ). На рис. 13 показаны эти зависимости а -A s для траекторий с углом 90°, а на рис. 14 – с углом 135°.
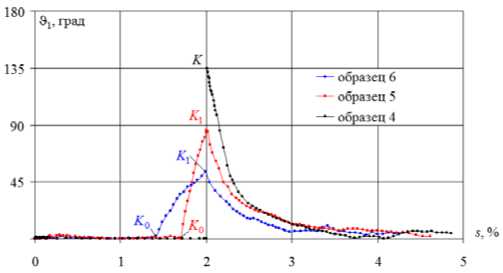
Рис. 10. Диаграмма характеристики векторных свойств материала 9 1 - 5
Fig. 12. The local chart of deformation 5 3 - Э 3
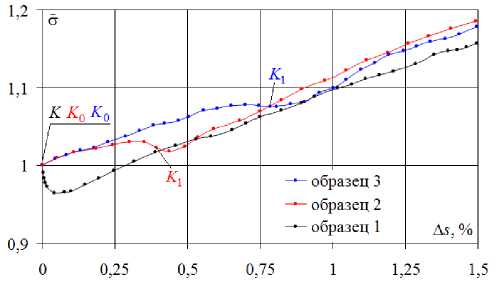
Рис. 13. Траектории с углом 90°. Диаграмма деформирования а-A 5
Fig. 13. Strain trajectories with an angle of 90°.
The chart of deformation 6 - A s
Fig. 10. The chart characterizing vector material properties 91 - 5
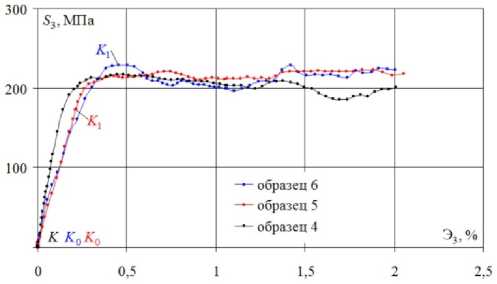
Рис. 12. Локальная диаграмма деформирования 5 3 - Э3
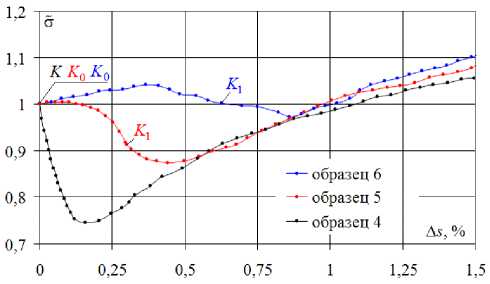
Рис. 14. Траектории с углом 135°. Диаграмма деформирования a-A s
Fig. 14. Strain trajectories with an angle of 135°. The chart of deformation a - A s
Из рис. 13, 14 видно, что для стали 3 во всех случаях после точки начала скругления K 0 величина σ сначала возрастает, причем ее увеличение тем больше, чем меньше кривизна κ 1 , т.е. больше радиус скругления R . Так, наибольшее возрастание σ на 7,8 % получено для κ 1 = 200 (образец 3, рис. 13). Для траекторий с кривизной κ 1 = 400 (образец 2 на рис. 13, образец 6 на рис. 14) возрастание σ составило 3–4 %.
На прямолинейных участках после точки K 1 можно наблюдать скалярные «нырки» напряжений, иными словами, убывание или «запаздывание» σ в зависимости от кривизны траектории деформирования, причем в данном случае уменьшение тем больше, чем больше кривизна κ 1 , т.е. меньше радиус скругления R . Более того, при больших значениях кривизны (например, образец 5 на рис. 14) величина σ начинает убывать уже на криволинейной части траектории. После завершения нырков при последующем росте деформации величина σ во всех случаях начинает возрастать и стремится к единой кривой при простом нагружении σ = Ф( s ) . Следует отметить, что в опытах И. Охаши [32, 33] с латунью (более мягким материалом) при скруглении угла излома ортогональной траектории понижение σ наблюдалось сразу после точки начала скругления.
Величина «нырка» напряжений зависит как от излома траектории, так и от кривизны участка. По полученным экспериментальным результатам построены графики зависимостей глубины скалярных нырков напряжений ∆σ от кривизны κ 1 (рис. 15).
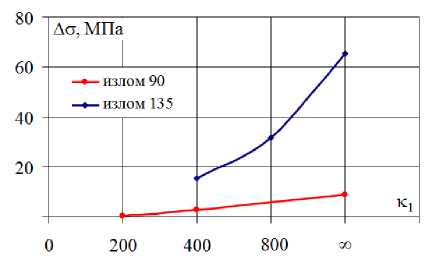
Рис. 15. Диаграммы ∆σ - κ 1
Fig. 15. Charts ∆σ - κ 1
При изломе на угол 90° (в точке излома κ 1 =∞ ) величина нырка составила ∆σ = 8,9МПа . Если это значение принять за 100 %, то при скруглении траектории кривизной κ 1 = 400 , величина нырка составила 31,5 % от ∆σ нескругленной траектории, а при значении κ 1 = 200 всего 5,6 %. Такие результаты говорят о малом влиянии сложного нагружения при данном угле излома траектории. При изломе на угол 135° величина ∆σ = 65,5 МПа , при скруглении траектории кривизной κ 1 = 800 , величина нырка составила 48,6 % от ∆σ не-скругленной траектории, а при значении κ 1 = 400 – 23,8 %. Таким образом, можно считать, что влияние сложного нагружения на зависимости между напряжениями и деформациями заметно проявляется при достижении некоторых предельных значений углов излома. Для рассматриваемого материала сталь 3 можно считать ϑ 1 0 > 90 ° .
На рис. 16, 17 показаны зависимости ϑ 1 -∆ s после начала скругления в точке K 0 (или излома K ).
Fig. 16. Strain trajectories with an angle of 90°. The chart ϑ 1 -∆ s
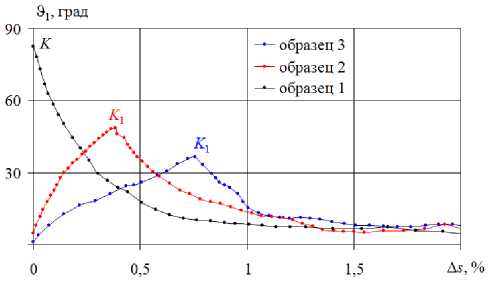
Рис. 16. Траектории с углом 90°. Диаграмма ϑ 1 -∆ s
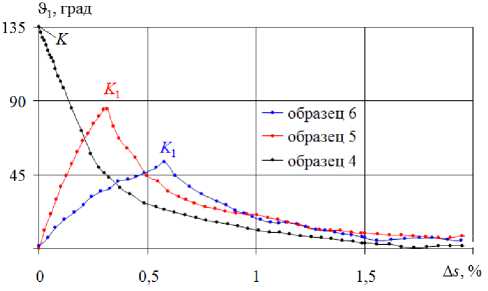
Рис. 17. Траектории с углом 135°. Диаграмма ϑ 1 -∆ s
Fig. 17. Strain trajectories with an angle of 135°.
The chart of deformation ϑ 1 -∆ s
Видно, что угол сближения ϑ 1 возрастает на участке скругления, при этом скорость возрастания выше при больших значениях кривизны κ 1 , т.е. при меньших радиусах скругления R . Это отражает влияние сложного нагружения на процесс деформирования через параметр кривизны. После окончания скругления начиная с точки K 1 значение ϑ 1 убывает вначале быстро, затем медленнее и с ростом деформации стремится к нулю. Аналогичные тенденции отмечены в опытах И. Охаши [32, 33] при скруглении угла излома ортогональной траектории.
На рис. 18 представлена диаграмма зависимости ϑ1 для прямолинейных участков после точки окончания скругления K1 от величины ∆s′ =∆s-x, где x – величи- на, на которую нужно сместить влево диаграмму до совпадения значений ϑ1 в точке K1 с соответствующим значением на диаграмме для двузвенной ломаной с углом излома 135° (образец 4), которая была взята за основу.
Видно, что при таком смещении с достаточной степенью точности экспериментальные точки ложатся на единую кривую, что подтверждает ее универсальность, также отмеченную в [32, 33].
образец 3 образец 2 образец 1
- образец б
• образец 5
• образец 4
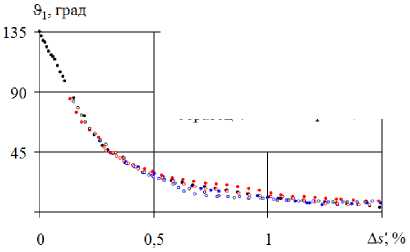
Рис. 18. Смещенная диаграмма ϑ 1 -∆ s ′
Таким образом, скорость уменьшения ϑ 1 при деформации вдоль прямолинейной траектории после точки K 1 мало зависит от различия геометрии траекторий (предшествующей деформации) до точки K 1 . Однако эти различия в геометрии траектории оказывают существенное влияние на само значение ϑ 1 в точке K 1 .
Заключение
Влияние сложного нагружения при переходе на криволинейный участок скругления проявляется не сразу. Для рассмотренного материала сталь 3 во всех случаях после точки начала скругления величина модуля напряжений сначала несколько возрастает (тем больше, чем меньше кривизна), а затем убывает с образованием «нырков», причем величина понижения модуля напряжений тем больше, чем больше кривизна. Точка минимума «нырка» во всех случаях находится на прямолинейной части траектории после скругления. При этом при больших кривизнах начало образования «нырка» наблюдается еще на криволинейной части траектории деформирования.
На участке скругления угол сближения ϑ 1 возрастает, причем чем больше кривизна траектории деформирования, тем выше скорость. После окончания скругления значение ϑ 1 убывает вначале быстро, затем медленнее и с ростом деформации стремится к нулю. При этом значение ϑ 1 , получившееся либо при изломе траектории, либо при деформировании по участку большой кривизны, при последующем деформировании по прямолинейному участку траектории убывает и стремится к нулю, а в процессе этого убывания зависимость ϑ 1 -∆ s ′ не зависит от истории нагружения. При последующем деформировании по прямолинейному участку после участка скругления экспериментальные результаты для скругленных и нескругленных траекторий становятся мало отличимыми друг от друга, таким образом, замена исходных неаналитических траекторий в виде двузвенных ломаных на гладкие траектории влияет на сложность процессов деформирования и нагружения материалов только в окрестности точки излома. При этом для углов излома 90° это влияние достаточно мало и, соответственно, будет малым и для углов излома менее 90°. Это обстоятельство можно учесть при численном моделировании процессов упругопластического деформирования материалов и интегрировании определяющих соотношений, заменяя неаналитические траектории гладкими.
Fig. 18. Offset сharts ϑ 1 -∆ s ′
Список литературы Влияние замены неаналитических траекторий с точками излома гладкими траекториями на сложность процессов деформирования и нагружения материалов
- Ильюшин А. А. О связи между напряжениями и малыми деформациями в механике сплошных сред // Прикладная математика и механика. – 1954. – Т. 18, № 6. – С. 641–666.
- Ильюшин А.А. Пластичность. Основы общей математической теории. – М.: Изд-во АН СССР, 1963. – 273 с.
- Ильюшин А.А. Механика сплошной среды. – М.: Изд-во МГУ, 1971. – 310 с.
- Ильюшин А.А. Труды (1946–1966). Т. 2. Пластичность. – М.: Физматлит, 2004. – 480 с.
- Ильюшин А.А., Васин Р.А., Моссаковский П.А. Теория упругопластических процессов при больших пластических деформациях // Прикл. проблемы механики тонкостенных конструкций. – М.: Изд-во Моск. ун-та, 2000. – С. 128–137.
- Ленский В.С. Экспериментальная проверка законов изотропии и запаздывания при сложном нагружении // Изв. АН СССР. ОТН. – 1958. – № 11. – С. 15–24.
- Lensky V.S. Analysis of plastic behavior of metals under complex loading // Plasticity. Proc., 2nd Symp. on Naval Struct. Mech. – Brown University, 1960. – Р. 259–278.
- Ленский В.С. Гипотеза локальной определенности в теории пластичности // Известия АН СССР, ОТН. – 1962. – № 5. – С. 154–158.
- Ленский В.С., Машков И.Д. Проверка законов в трехмерном пространстве девиатора деформаций // Упругость и неупругость. – М.: Изд-во Моск. ун-та, 1971. – № 2. – С. 58–166.
- Ленский В.С. Физическая достоверность в современной теории пластичности // Упругость и неупругость. Ч. 1. – М.: Изд-во Моск. ун-та, 1993. – С. 95–119.
- Жуков А.М. Сложное нагружение и теория пластичности изотропных материалов // Изв. АН СССР. ОТН. Механика и машиностроение. – 1955. – № 8. – С. 81–92.
- Жуков А.М. О пластических деформациях изотропного материала при сложном нагружении // Изв. АН СССР ОТН. Механика и машиностроение. – 1956. – № 12. – С. 72–87.
- Жуков А.М. Некоторые особенности поведения металлов при упругопластическом деформировании // Вопросы теории пластичности. – М.: Изд-во АН СССР, 1961. – С. 30–57.
- Жуков А.М. О свойствах запаздывания в общей теории пластичности // Изв. РАН. МТТ. – 1992. – № 5. – С. 110–119.
- Васин Р.A. Некоторые вопросы связи напряжений и деформаций при сложном нагружении // Упругость и неупругость. Вып. 1. – М.: Изд-во МГУ, 1971. – С. 59–126.
- Васин Р.А, Ильюшин А.А. Об одном представлении законов упругости и пластичности в плоских задачах // Извес-тия АН СССР. МТТ. – 1983. – № 4. – С. 114–118.
- Васин Р.А. Определяющие соотношения теории пластичности // Итоги науки и техники. ВИНИТИ. Серия: Механика деформируемого твердого тела. – 1990. – Т. 21. – С. 3–75.
- Васин Р.А. Теория упругопластических процессов и исследование структурно-механических свойств материалов // Изв. РАН. МТТ. – 2011. – № 1. – С. 19–26.
- Васин Р.А. О «памяти» материала в теории упруго-пластических процессов // Известия Тульского государственного университета. Естественные науки. – 2013. – № 2–2. – С. 59–70.
- Васин Р.А. Экспериментальное исследование неупругого поведения материалов // Прикладная механика и техническая физика. – 2016. – № 5. – С. 30–34. DOI: 10.15372/PMTF20160504
- Дао Зуй Бик. О гипотезе локальной определенности в теории пластичности // Вестник Моск. ун-та. Математика, механика. – 1965. – № 2. – С. 67–75.
- Дао Зуй Бик. Модификация соотношений упругопластических процессов средней кривизны // Вестник Моск. ун-та. Математика, механика. – 1981. – № 5. – С. 103–106.
- Dao Huy Bich. A boundary value problem of elastoplastic deformation process theory: Existence and uniqueness theorems // The Journal of the Australian Mathematical Society. Series B. Applied Mathematics. – 1994. Vol. 35(4). – P. 506–524. DOI: 10.1017/S0334270000009589
- Москвитин В.В. Пластичность при переменных нагружениях. – М.: Издательство МГУ, 1965. – 263 с.
- Дегтярев В.П. Пластичность и ползучесть машиностроительных конструкций. – М.: Машиностроение, 1967. – 130 с.
- Дегтярев В.П. Новые прикладные задачи экспериментальной механики деформируемого тела // Упругость и неупругость. – М.: Изд-во Моск. ун-та, 2001. – С. 171–174.
- Кравчук А.С. О методе последовательных приближе-ний в теории пластичности при сложном нагружении // Изв. АН СССР. МТТ. –1970. – № 4. – С. 188–191.
- Кравчук А.С. О теории пластичности для траекторий деформаций средней кривизны // Упругость и неупругость. – М.: Изд-во Моск. ун-та, 1971. – № 2. – С. 91–100.
- Кравчук А.С. Применение понятий простого и сложного нагруженией по А.А. Ильюшину в теории контакта твердых тел // Упругость и неупругость. – М.: Изд-во Моск. ун-та, 2001. – С. 182–187.
- Малый В.И. Об упрочнении функционалов теории упругопластических процессов // Прикладная механика. – 1978. – Т. 14, № 2. – С. 48–53.
- Малый В.И. О подобии векторных свойств материалов в упругопластических процессах // Прикладная механика. – 1978. – Т. 14, № 3. – С. 19–27.
- Некоторые экспериментальные данные об общем законе теории пластичности Ильюшина / И. Охаши, М. Токуда, И. Курита, Т. Сузуки // Изв. АН СССР. МТТ. – 1981. – № 6. – С. 53–63.
- Experimental Examination of the hypothesis of local de-terminability in the plastic deformation of metals / Y. Ohashi, Y. Kurita, T. Suzuki, M. Tokuda // Journal of the mechanics and phys-ics of solids. – Oxford, New York, Frankfurt: Pergamon Press, 1981. – Vol. 29. – № 1. – P. 51–67. DOI: 10.1016/0022-5096(81)90015-6
- Ohashi Y., Tanaka E. Plastic deformation behavior of mild steel along orthogonal trilinear strain trajectories in three-dimensional vector space of strain deviator // Journal of Engineer-ing Materials and Technology, Transactions of the ASME. – 1981. – Vol. 103(4). – P. 287–292. DOI: 10.1115/1.3225018
- Effect of curvature of the strain trajectory on the plastic behaviour of brass / Y. Ohashi, Y. Kurita, T. Suzuki, M. Tokuda // Journal of the Mechanics and Physics of Solids. – 1981. – Vol. 29(1). – P. 69–86. DOI: 10.1016/0022-5096(81)90016-8
- Ohashi Y., Ohno N. Inelastic stress-responses of an alu-minium alloy in non-proportional deformations at elevated temper-ature // Journal of the Mechanics and Physics of Solids. – 1982. – Vol. 30(5). – P. 287–304. DOI: 10.1016/0022-5096(82)90001-1
- Tokuda M., Ohashi Y., Iida T. On the hypothesis of local determinability and a concise stress-strain relation for curved strain path // Bulletin of the JSME. – 1983. – Vol. 26(219). – P. 1475–1480. DOI: 10.1299/jsme1958.26.1475
- Шевченко Ю.Н., Терехов Р.Г. Физические уравнения термовязкопластичности. – Киев: Наукова думка, 1982. – 238 с.
- Шевченко Ю.Н., Бабешко М.Е., Терехов Р.Г. Термо-вязкоупругопластические процессы сложного деформирования элементов конструкций. – Киев: Наукова думка, 1992. – 327 с.
- Определяющие уравнения процессов термовязкопла-стического деформирования элементов тела по траекториям произвольной кривизны и малого кручения / Ю.Н. Шевченко, Р.Г. Терехов, Н.С. Брайковская, Н.Н. Тормахов // Прикладная механика. – 2002. – Т. 38, № 7. – С. 64–73.
- Зубчанинов В.Г. Механика процессов пластических сред. – М.: Физматлит, 2010. – 352 с.
- Зубчанинов В.Г. Устойчивость и пластичность. Т. 2. Пластичность. – М.: Физматлит, 2008. – 336 с.
- Зубчанинов В.Г. Постулат изотропии и закон сложной разгрузки сплошных сред // Известия РАН. Механика твердого тела. – 2011. – № 1. – С. 27–37. DOI: 10.3103/S0025654411010043
- Зубчанинов В.Г. Общая математическая теория пластичности и постулаты макроскопической определимости и изотропии А.А. Ильюшина // Вестник Московского университа. Серия 1. Математика. Механика. – 2018. – № 5. – С. 29–46. DOI: 10.3103/S0027133018050011
- Зубчанинов В.Г., Охлопков Н.Л., Гараников В.В. Экспериментальная пластичность: в 2 кн. Книга 1. Процессы сложного деформирования. – Тверь: Изд-во ТГТУ, 2003. 172 с; Книга 2: Процессы сложного нагружения. – Тверь, 2004. – 184 с.
- Зубчанинов В.Г., Алексеев А.А., Гультяев В.И. Моде-лирование процессов упругопластического деформирования материалов по многозвенным кусочно-ломаным прямолиней-ным траекториям // Вестник Пермского национального иссле-довательского политехнического университета. Механика. – 2017. – № 3. – С. 203–215. DOI: 10.15593/perm.mech/2017.3.12
- Experimental verification of postulate of isotropy and mathematical modeling of elastoplastic deformation processes following the complex angled nonanalytic trajectories / V.G. Zub-chaninov, A.A. Alekseev, E.G. Alekseeva, V.I. Gultiaev // Materi-als Physics and Mechanics. – 2017. – Vol. 32, no. 3. – P. 298–304. DOI: 10.18720/MPM.3232017_10
- Зубчанинов В.Г., Алексеев А.А., Алексеева Е.Г. Проверка постулата изотропии и численное моделирование про-цессов деформирования материалов на сложных гладких траекториях // Materials Physics and Mechanics. – 2016. – Т. 29, № 2. – С. 150–157.
- Modeling of elastoplastic steel deformation in two-link broken trajectories and delaying of vector and scalar material properties / V.G. Zubchaninov, E.G. Alekseeva, A.A. Alekseev, V.I. Gultiaev // Materials Physics and Mechanics. – 2019. – Vol. 42. – Р. 436–444. DOI: 10.18720/MPM.4242019_8
- Процессы сложного нагружения конструкционной стали по пятизвенной кусочно-ломаной траектории деформирования / В.Г. Зубчанинов, А.А. Алексеев, В.И. Гультяев, Е.Г. Алексеева // Вестник Томского государственного университета. Математика и механика. – 2019. – № 61. – C. 32–44. DOI: 10.17223/19988621/61/4
- Modeling of elastoplastic deformation of structural steel by a trajectory containing three circles touching internally / V.G. Zub-chaninov, A.A. Alekseev, V.I. Gultiaev, E.G. Alekseeva // Materials Physics and Mechanics. – 2019. – Vol. 42, № 5. – С. 528–534.
- Поздеев А.А., Трусов П.В., Няшин Ю.И. Большие упругопластические деформации: теория, алгоритмы, приложе-ния. – М.: Наука, 1986. – 232 с.
- Трусов П.В., Швейкин А.И., Янц А.Ю. Основные положения теории упругопластических процессов А.А. Ильюшина: анализ с позиций многоуровневого моделирования для случая больших градиентов перемещений // Упругость и неупругость: материалы Международного научного симпозиума по проблемам механики деформируемых тел, посвященного 105-летию со дня рождения А.А. Ильюшина. – М.: Изд-во МГУ, 2016. – C. 119–126.
- Коровин И.М. Некоторые вопросы пластичности материалов при нагружении по траекториям с точкой излома // Изв. АН СССР. МТТ. – 1969. – № 3. – С. 152–158.
- Tanaka E. Hypothesis of Local Determinability for Five-Dimensional Strain Trajectories // Acta Mechanica. – 1984. – Vol. 52. – P. 63–76. DOI: 10.1007/BF01175965
- Экспериментальное исследование процессов деформирования стали по двузвенным траекториям / A.A. Лебедев, Б.И. Ковальчук, Н.М. Кульчицкий, А.Ф. Хакимов // Проблемы прочности. – 1988. – № 3. – С. 7–10. DOI: 10.1007/BF01529738
- Babamuratov K.Sh., Abirov R.A. The new approach to the analysis of elasto-plastic deformation of solids within the bounds of theory of processes by A.A. Ilyushin // ASME International Mechanical Engineering Congress and Exposition, Proceedings. – 2001. – P. 899–903.
- Пелешко В.А. Прикладной и инженерный варианты теории упругопластических процессов активного сложного нагружения. Часть 1: Условия математической корректности и методы решения краевых задач // Изв. РАН. МТТ. – 2015. – № 6. – С. 61–68. DOI: 10.3103/S0025654415060060
- Пелешко В.А. Прикладной и инженерный варианты теории упругопластических процессов активного сложного нагружения. Часть 2: Идентификация и верификация // Изв. РАН. МТТ. – 2016. – № 1. – С. 110–135. DOI: 10.3103/S0025654416010106
- Муравлев А.В. Экспериментальное построение функционалов пластичности для траекторий деформаций типа двухзвенных ломаных в опытах на сплошных цилиндрических областях // Вестник Московского университета. Серия 1: Математика. Механика. – 1996. – № 5. – С. 74–80.
- Муравлев А.В. О представлении упругого потенциала в обобщенном пространстве деформаций А.А. Ильюшина // Известия РАН. Механика твердого тела. – 2011. – № 1. – С. 99–112.
- Молодцов И.Н., Бабаева Д.О. Некоторые вопросы верификации теории упругопластических процессов при сложном нагружении // Проблемы машиностроения и автоматизации. – 2016. – № 3. – С. 98–105.


