Влияние жесткости механической части привода и параметров резания на управление упругими деформациями формообразования

УДК 621.9:531.3                                           

Funding information: The research is done with the financial support from RFFI (grants nos. 19-08-00022 and 20-3890074).

Введение. Синергетическая парадигма привела к пересмотру многих подходов к анализу свойств систем, взаимодействующих с различными средами [1–19]. Она используется при изучении процесса резания, как единой нелинейной динамической системы, в которой рассматриваются различные физические процессы, характеризующие состояние системы [10–18]. Системно-синергетический подход лежит в основе синергетической теории управления, а также управления процессами обработки на станках [18–24]. В таком случае обеспечивается согласование внешнего управления с внутренней динамикой резания [23–25]. Проблемы синергетического согласования актуальны при обработке маложестких деталей, у которых априорно задан закон ее изменения вдоль траекторий движения инструмента [13, 26–29]. Во всех указанных случаях необходимо осуществлять управление упругими деформационными смещениями вершины инструмента и заготовки в точке контакта с ней инструмента. Необходимо отметить, что погрешности геометрической топологии детали, формируемой резанием, на 60–80 % обусловлены упругими деформационными смещениями элементов системы резания [11, 13, 30]. Основные направления совершенствования систем управления процессами обработки на станках связаны с объединением собственно станка и ЭВМ [30–33]. Проблема же управления упругими деформационными смещениями инструмента и заготовки сформулирована еще в работах [34]. Наконец, синергетический подход к анализу и синтезу систем управления процессами обработки на станках, сформулированный в работах [23–25], поставил задачу построения систем управления процессами обработки на станках с ЧПУ на основе согласования программы исполнительных элементов станка с эволюционно изменяющимися свойствами процесса резания. Такой подход использован и при совершенствовании систем управления сверлением глубоких отверстий малого диаметра, а также при обеспечении устойчивости траекторий формообразующих движений [25, 35]. Таким образом, как при управлении процессами обработки на станках, так и при программировании траекторий формообразующих движений необходимо знать законы преобразования управляемых траекторий исполнительных элементов

Машиностроение и машиноведение

станка в силы резания и, как следствие, при заданных упругих свойствах подсистем инструмента и заготовки в упругие их деформации. Они непосредственно влияют на параметры точности изготовления деталей. На законы преобразования влияет жесткость механической части приводов исполнительных элементов станка и параметры, характеризующие состояние процесса резания. Именно раскрытию влияния этих параметров на преобразование программируемых траекторий серводвигателей в силы резания посвящено исследование, приведенное в статье. Оно направлено на повышение эффективности управления точностью изготовления деталей.

Материалы и методы . Рассмотрим продольное точение вала постоянного диаметра, в котором задан закон изменения его жесткости в направлении, нормальном к оси вращения (рис. 1). При описании преобразования траекторий серводвигателей в силы, действующие на инструмент, примем следующие гипотезы:

• 1.    Рассмотрим случай, при котором заданная вдоль оси вращения жесткость с ( L ) заготовки на порядок меньше жесткости подсистемы инструмента (рис. 1). Поэтому деформациями инструмента относительно несущей системы станка можно пренебречь.

• 2.    Будем считать заданными и управляемыми в пределах полос пропускания серводвигателей траектории вращения шпинделя и привода суппорта. Инерционность механической части привода подачи отнесем к ротору двигателя подачи. Она влияет на переходные процессы в серводвигателе.

• 3.    Реакцией на скорости серводвигателей со стороны процесса резания пренебрегаем. Это справедливо, если мощность резания, приведенная к роторам двигателей, существенно меньше мощности серводвигателей.

• 4.    Будем рассматривать, кроме упругости заготовки, упругость всей механической части привода подачи, которую учтем обобщенной жесткостью с ₀. Так как в процессе обработки реверсирование привода подачи отсутствует, то жесткость с ₀ можно считать постоянной на всей траектории движения суппорта.

• 5.    Для формирования сил при постоянной скорости резания примем гипотезу об их зависимости от площади срезаемого слоя. Запаздыванием сил по отношению к изменению площади среза пренебрегаем [2324].

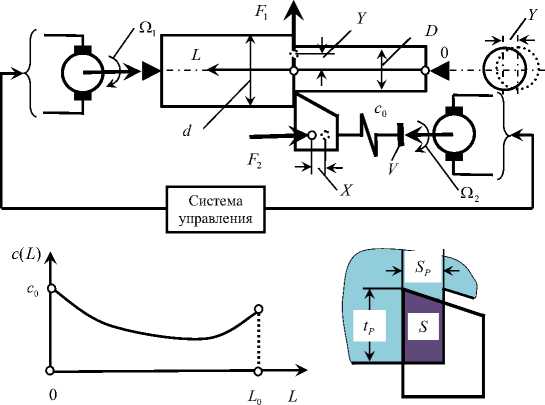
Рис. 1. Схема динамической системы преобразования траекторий исполнительных элементов станка в силы резания Тогда модуль силы резания пропорционален площади срезаемого слоя

F(t) = %, Х 2 } T ,                                            (1)

где F ₀ = р S — модуль силы резания в [ кг ] ;

р — давление стружки на переднюю поверхность инструмента в [ кг / мм ² ] ;

S — площадь срезаемого слоя в [ мм ² ] ;

X1,Х2  — безразмерные коэффициенты. Связь скорости подачи V и упругих деформационных смещений X и Y определяется из системы (рис. 1).

t

<

c 0 X = Х 2 Р ( t p - Y ) J [ V © - v ( ^ )] d ^ ;

t - T

t

c(L)Y = XiP(tp - Y) J [V© - V(^)]d^, t - T где v(t) = dX / dt; V(t) = kQ2 (t);

k — коэффициент, определяющий связь частоты вращения привода подачи и скорости суппорта в [ мм ] .

Частоты Q ₁ и Q ₂ рассматриваются в [ с " ' ] . Поэтому время T в интегральном операторе формирования подачи T = ( Q ₁ ) ^{- 1} = const .

Изучение преобразования скорости подачи V в силы резания удобно выполнить в частотной области.

Для этого можно воспользоваться преобразованиями Лапласа и Фурье [36]. Однако система (2) имеет не только запаздывающие аргументы, но и мультипликативные члены. Использование же методов преобразования Лапласа и Фурье возможно лишь для линейных систем. Поэтому исследование выполним в два этапа. На первом этапе в (2) положим Y ^ 0 по сравнению с глубиной резания tp. преобразование скорости подачи в силы на основе выражения

С0X = X2ptp J [V(^) - v(^)ld^- t - T

Нетрудно показать, что передаточная функция W(p) = F(p)/ V(p) равна w (p) = с1"exp(-Tp)--------1-------- p 1 + с^ [1 - exp(-Tp)]

c ₀

Тогда проанализируем

где с = p t_p x ₂ имеет смысл жесткости процесса резания. Выражение (4) позволяет выяснить частотные свойства преобразования скорости подачи V в силу резания F в зависимости от безразмерного параметра А = c_L / c 0 . Этот параметр определяет отношение жесткости процесса резания к жесткости

_                           .             .      1 - exp(-Tp) _ механической части привода подачи. При А ^ 0 передаточная функция W(p) ^ с           . При А ^ да

p

с

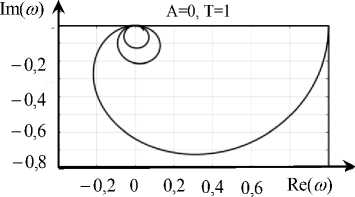
W(p) ^ — . Это два крайних случая. Если случай А ^ 0 возможен при существенном увеличении жесткости p механической части привода по сравнению с жесткостью процесса резания, то второй случай требует уменьшения жесткости привода до нуля, что для реальных систем невозможно. Приведем примеры W(jю) для различных A (рис. 2). Амплитуда рассмотрена в относительных единицах к с^ = 1.

Mod[W]

Mod[W]

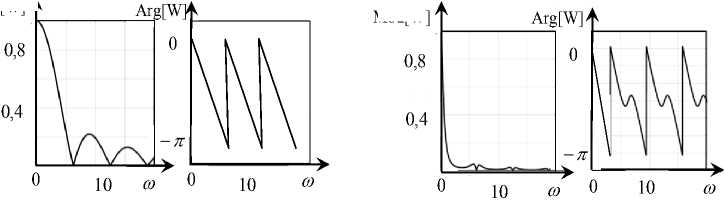
а )

б )

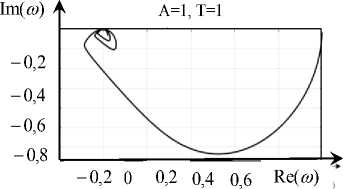
Рис. 2. Пример частотных характеристик преобразования скорости подачи в модуль силы резания: а–А=0, б–А=1

Машиностроение и машиноведение

Вначале рассмотрим случай, когда деформации механической части между ротором двигателя подачи и перемещением суппорта отсутствуют (рис. 2 а). Такая частотная характеристика обусловлена свойством интегрального

t оператора J V(£)d^ t - T

формирования величины подачи, который раскрывает тот факт, что

величина подачи есть путь, пройденный инструментом относительно заготовки в течение периода ее вращения. Естественно, что составляющие изменения скорости подачи, частота которых равна или кратна частоте вращения заготовки, после интегрирования обращаются в ноль. Это частоты, на которых Mod[W(jю)] = 0 (рис. 2). При этом наблюдается быстрое вращение фазы на частотах, близких к частоте вращения заготовки, что способствует самовозбуждению систем управления процессом резания. Увеличению податливости механической части привода соответствует изменение частотных свойств преобразования скорости V в силы резания. Во-первых, полоса пропускания этого преобразования заметно уменьшается, что должно способствовать увеличению времени переходного процесса при установлении нового значения управляемых сил резания. Во-вторых, периодические вариации фазы наблюдаются в области большего затухания амплитуды. Наконец, при еще больших увеличениях податливости характеристики преобразования скорости в силы приближаются к интегрирующему звену. В основе механизма затягивания переходного процесса лежит перераспределение сил, влияющих на деформационные смещения, и деформационных смещений, влияющих, в свою очередь, на силы. Этот функционально связанный процесс зависит от жесткости механической части привода подачи.

Приведенный анализ позволяет также оценить влияние на динамику преобразования скорости V в силы резания деформационных смещений заготовки в направлении оси ее вращения (направление Y на рис. 1). Очевидно, что при уменьшении жесткости c уменьшается и параметр А, влияющий на динамику преобразования скорости подачи в силы резания.

Алгоритм вычисления траектории скорости подачи. Для обеспечения заданных значений диаметра путем управления деформацией Y необходимо подобрать такие траектории скорости V , при которых

Y = const . Для этого вместо интегрального оператора в (2) рассмотрим его первообразные, то есть

Г c 0 X = Х 2 р ( t p - Y )[ L ( t ) - L ( t - T ) - X ( t ) + X ( t - T )];

1 c ( L ) Y = X i P ( t p - Y )[ L ( t ) - L ( t - T ) - X ( t ) + X ( t - T )],

t где L(t) — траектория перемещения суппорта без учета упругих деформаций, то есть L(t) = J V(£)d5,. В (5) 0

L ( t ) - L ( t - T ) = S P °’( t ) — текущее значение подачи без учета деформационных смещений. Если c ( L ) = const и рассматривается     установившееся     состояние ( X ( t ) = X ( t - T )),     то      S_p ° = S_p = VT .     Здесь

SP(t) = Sp° -[X(t)-X(t-T)]. Подчеркнем, что величина подачи Sp°, оцениваемая традиционно, отличается от действительного ее значения Sp (t).

Будем вычислять деформационные смещения в (5) последовательно после каждого оборота заготовки и определим       последовательности       X(iT) = {X (0), X (T),... X (nT)},       Y(iT) = {Y (0), Y (T ),...Y (nT)}, i=n

S_P(t) = { S_p ( T ),.. S P ( nT )}, c(T) = { c [ S P (T )],... c [( E S P ( iT )]}. Таким образом, за n оборотов заготовки суппорт i = 1

i=n проходит расстояние L(n) =E Sp (iT). В этих последовательностях X(0) = Y(0) = 0. Можно рассмотреть i=1

решение двух задач.

Первая задача анализа, то есть определения траекторий деформационных смещений X(iT) и Y(iT) при постоянной скорости подачи. Для вычисления значений X(T), Y(T)  и последующих величин деформационных смещений X(iT), Y(iT) можно воспользоваться соотношениями, в которых известны все l=i-1

предыдущие значения X [( i - 1) T )], Y [( i - 1) T )], а также c [( E S P ( IT )]. Здесь V = const , следовательно, l = 1 l = i - 1

c [( E S P ( IT )] = ( c ( iS P ). Таким образом, для вычисления X ( iT ), Y ( iT ) можно воспользоваться системой l = 1

c_zZ® = F ^(,),                                                             (6)

где Z^(,) = { Y ( iT ), X ( iT )} ^T ; F ) = p S^t p + X (( i - 1) T )]{ _X 2 , X 1 } T ;

с _Σ

c 0 + ^X 2 ^P t P       ^X 2 ^{P S}P

X 1 P t P     К c ⁽ iS P ) + X 1 P S P⁰’

В (5) отброшены мультипликативные члены от деформационных смещений, которые являются малыми величинами. При заданной скорости V = const нас интересует прежде всего закон изменения деформационных смещений Y(iT) = {У(0),У(T),...У(nT)}, который характеризует погрешность диаметра. На основе (6) для деформационных смещений У(iT), непосредственно влияющих на диаметр детали, получаем

_{У (} iT ) ₌ Х 2 Р c ( iS P ) S P °’{ t P + X [( i - 1) T )]} c 0 c ( iS P ) + X 1 P c 0 S p +X 2 P c ( S ) t P

Таким образом, У(iT) зависят не только от закона распределения жесткости заготовки c(L) по пути резания L , но и от дc(L)/ дL , влияющего на У(t - T). На силы резания, следовательно, диаметр D , влияет давление стружки р. Оно меняется, например, по мере нарастания износа инструмента, изменения его геометрии, условий обработки и свойств обрабатываемого материала.

Вторая задача синтеза, то есть определения последовательности S_P(t) = { S P (T ),... S_P ( nT )} и соответствующей ей скорости V ( t ) таким образом, чтобы выполнялось условие У ( iT ) = const , У ( iT ) е Y(iT). Это условие постоянства диаметра при заданном законе c ( L ) при прочих неизменных условиях. Заметим, что постоянные составляющие в деформационных смещениях Y(iT) не имеют принципиального значения, так как могут учитываться с помощью статической установки инструмента [34]. Для определения закона изменения величины подачи на каждом обороте заготовки по критерию обеспечения постоянства диаметра необходимо в (7) положить У ( iT ) = const . Тогда необходимо вычислить последовательность S_P (t) = { S_P(T ),... S_P ( nT )}. Процедура вычисления на i -ом обороте заготовки заключается в определении S_P ( iT ) при условии, что заданы

S p ( iT ) =

У * c [( £ S p ( IT )]{ c 0 + X 2 P t p }

_____________ l =1 ________________________________________________

X1Pco{tp + X[(i - 1)T] - У •} где У * = const — заданная величина упругих деформационных смещений.

В (8) значение жесткости заготовки берется средним в течение каждой подачи. Тогда на основе вычисленных S_P(t) = { S_P(T ),... S_P ( nT )}определяются закон изменения V ( t ) и, следовательно, программируемая траектория скорости подачи во времени или пути. Вычисление траектории V ( t ) осуществляется на основе решения обратных задач динамики [37-38].

Результаты исследования . Для обеспечения точности изготовления маложестких валов необходимо согласовать траектории исполнительных элементов станка с изменяющейся жесткостью заготовки вдоль траектории движения инструмента. Согласование необходимо выполнить и в том случае, если учитываются эволюционные изменения свойств процесса резания, обусловленные, например, изнашиванием инструмента или термодинамическими процессами, а также регулярными возмущениями, к примеру, вариациями припуска. Для этого прежде всего требуются знания законов преобразования программируемой скорости подачи суппорта в силы резания и далее в сами деформации, изменяющие текущее значение диаметра заготовки. Выполненные исследования показали, что закон преобразования зависит от параметров жесткости взаимодействующих подсистем и параметров динамической связи, формируемой процессом резания.

Машиностроение и машиноведение

Среди параметров жесткости принципиальное значение имеют характеристики жесткости механической части приводов подачи, которые можно оценить суммарной приведенной жесткостью c0 . Она изменяет амплитудно-фазовую частотную характеристику преобразования скорости подачи в силы резания (рис. 2). Как видно, уменьшение жесткости привода существенно уменьшает амплитуду по мере роста частоты и изначальная АФЧХ, которая имела заметные всплески, преобразуется в характеристику с амплитудным затуханием. Такая характеристика вызывает преобразования колебательных переходных процессов в монотонные, близкие к апериодическим. По мере уменьшения c0 наблюдается уменьшение частоты среза в преобразовании скорости подачи в силы резания (рис. 2), следовательно, возрастает время переходного процесса, например, изменения силы резания при врезании инструмента. Пример изменения переходных процессов установления силы F0 при точении вала из стали 20Х диаметром 80 мм приведен на рис. 3. Точение на режимах: скорость резания 4,0 м/с (частота вращения шпинделя — 1000 об/мин), глубина резания tP — 2,0 мм, величина подачи SP — 0,1 мм. Для этого случая р = 400 кг / мм2.

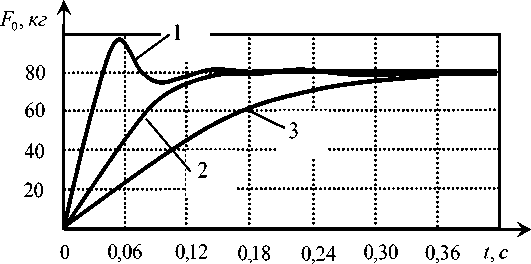
Рис. 3. Пример изменения переходных процессов установления силы:

F ₀ : 1 — с 0 = 1000 кг/мм, 2 — с 0 = 750 кг/мм, 3 — с 0 = 500 кг/мм

Из отмеченных выше свойств интегрального оператора формирования величины подачи следует важное заключение о возможности управления силами резания, следовательно, упругими деформационными смещениями инструмента относительно заготовки. При изменении скорости подачи частотные составляющие возмущений, равные или кратные частоте вращения заготовки, становятся неуправляемыми с помощью вариации скорости привода подачи. Например, это вариации припуска, обусловленные несоосностью установки заготовки, радиальные биения шпинделя и пр. Приведенные данные также показывают, что переходные процессы преобразования скорости подачи в силы зависят также от параметров динамической связи, формируемой процессом резания, и прежде всего от параметра давления стружки на переднюю поверхность инструмента. Этот параметр изменяется по мере развития износа инструмента. На динамику преобразования траекторий исполнительных элементов станка в силы резания оказывают влияние все факторы, связывающие силы резания с площадью срезаемого слоя. Эти факторы ограничивают возможности управления точностью изготовления деталей путем варьирования траекторий исполнительных элементов станка. Это относится прежде всего к обработке деталей сложной геометрической формы.

Обсуждение и заключения . Одно из направлений повышения точности изготовления деталей на станках связано с согласованием программы ЧПУ с изменяющимися динамическими свойствами процесса резания. Причем эти изменения могут быть заданы априорно. Например, априорно может быть задан закон изменения матриц жесткости вдоль траектории исполнительных элементов станка. Они могут развиваться по некоторому случайному закону, например, в связи с развитием износа инструмента. Во многих случаях управление точностью осуществляется на основе изменения упругих деформационных смещений инструмента и заготовки. Как показано в статье, закон преобразования скорости подачи в силы резания и упругие деформационные смещения, во-первых, зависит от параметров упругости механической части приводов подачи, влияя не только на время переходных процессов, но и на их форму. Во-вторых, закономерности преобразования скорости подачи в силы зависят от эволюции параметров взаимодействующих подсистем со стороны инструмента и заготовки, а также параметров формируемой резанием динамической связи. Раскрытые закономерности преобразования позволяют не только выяснить ограничения, накладываемые системой резания на возможности управления точностью, но и повысить их точность.

Библиографический список