Влияние зональной неоднородности коллектора на распределение давления в пласте
Автор: Брайцева Е.Е.
Журнал: Форум молодых ученых @forum-nauka
Статья в выпуске: 10 (38), 2019 года.
Бесплатный доступ
В статье на основе конечно-разностной модели поля давления в зонально-неоднородном пласте, рассмотрена проблема фильтрации в пластах с загрязненной призабойной зоной. Путем сопоставления с аналитическим решением и результатами моделирования в гидродинамическом симуляторе показана достоверность развитой модели.
Давление, фильтрация, неоднородный пласт, конечно-разностная модель
Короткий адрес: https://sciup.org/140285108
IDR: 140285108 | УДК: 532.54
Текст научной статьи Влияние зональной неоднородности коллектора на распределение давления в пласте
Задачи о полях давления в проницаемых пластах составляют теоретическую основу разработки нефтегазовых месторождений, об их актуальности свидетельствует большое количество классических и современных работ [1 – 5].
Результаты исследования полей давления в пористых пластах, используются при расчетах параметров отбора и закачки в гидрогеологии, нефтегазовой промышленности и экологии [1 – 5].
В природе все пласты неоднородны. Часто встречающимся типом неоднородности является зональная неоднородность горных пород [4], то есть, проницаемость меняется с удалением от скважины. Такая неоднородность неизбежно возникает и в процессе эксплуатации залежи, так как околоскважинная зона со временем загрязняется. Именно изучению изменению давления и притока в результате такого загрязнения посвящена данная работа.
Для описания фильтрации в неоднородном пласте предлагается следующая модель. Пласт шириной H вскрыт идеально, на границе при x = 0 поддерживается постоянное давление P 0, течение флюида полагается плоским. На правой границе пласта поддерживается гидростатическое давление Pk . Зональная неоднородность пласта учитывается зависимостью коэффициента проницаемости от координаты x . Геометрия задачи представлена на рис. 1.

Рис.1. Геометрия задачи
Течение флюида в пористых пластах описывается уравнением
пьезопроводности дР д дР
) = О'
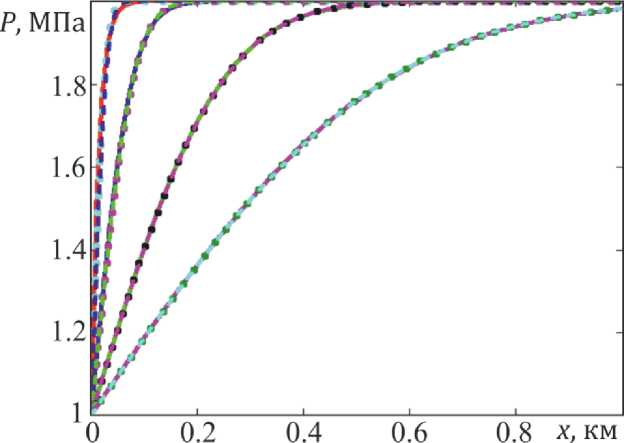
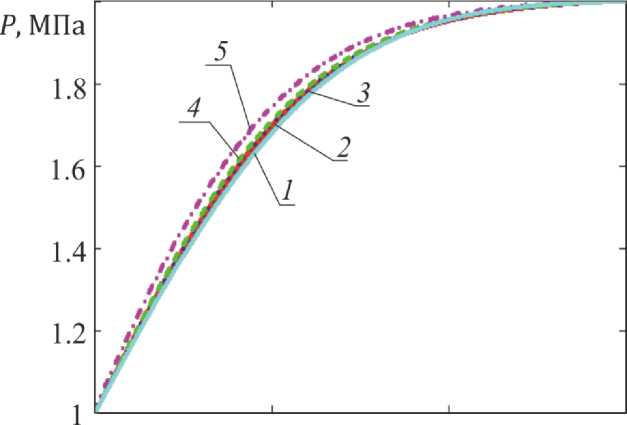
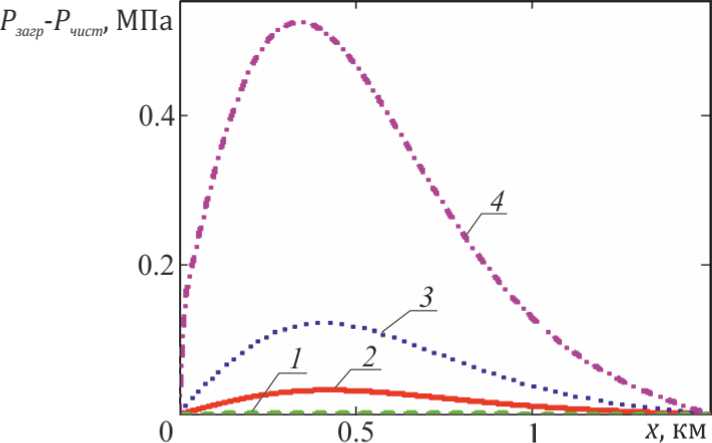
И(тРж... ^р.^^-^^дХ t > 0, 0 В начальный момент во всем пласте давление равно гидростатическому P|t=o = Pt, 0 < x < L. На правой границе изменение давления отсутствует, и равно первоначальному давлению в системе Р|х=1 = Рк, t > 0. Пласт эксплуатируется в режиме постоянной депрессии Р|,=о = Ро , t > 0. Решить задачу (1) - (4) аналитическим методом не представляется возможным, поэтому, использован конечно-разностный подход. В основу алгоритма положена неявная схема на равномерной сетке с шагом □ по координате х, шаг по времени принят равным т. Применение неявной схемы несмотря на сложность ее реализации по сравнению с явной обусловлено тем, что неявная схема является абсолютно устойчивой, следовательно для расчетов не требуется выполнения условий устойчивости, что дает свободу в выборе величины шагов по координате и времени. Конечно - разностный аналог уравнения (1) представлен в виде системы линейных алгебраических уравнений (СЛАУ)[6, 7] ™ р— - (1 + ^ (z + Zi+t)) Ph + T^ p+ = -pH, (5) где Р^ - значения искомого поля давления в узлах равномерной сетки, i е [0,N1], к е [0, N2], где N1 + 1,,N2 + 1 - количество узлов сетки по оси х и времени t, соответственно. Полученная СЛАУ решается с помощью метода прогонки [6, 7]. Аналитическое решение частного случая задачи (1) – (4), когда коэффициент проницаемости не зависит от x приведен в работе [4] и имеет вид: Р = р0 + (pt- ро)е* (^ (6) Для верификации расчетов, проведенных по конечно-разностной модели, проведено их сопоставление с аналитическим решением и результатами моделирования в eclipse (рис. 2). Для этого пласт полагается однородным, с проницаемостью k = 10-15 м2 значения других физических параметров пласта: т = 0.2, в ж = 2^10 9"^,^с = 10 9~,М = 5 мПа • с, Р0 = 1 МПа, Рк = 2 МПа. При моделировании в eclipse рассмотрены так же следующие исходные данные: эффективная толщина пласта H = 8 м, скин фактор – 0, отношение горизонтальной проницаемости к вертикальной – 1. Рис. 2. Распределение давления по пласту, рассчитанное в eclipse На рис. 3 приведено сопоставление пространственного распределения давления для расчетов по формуле (6) (пунктирные линии) и конечно – разностной схеме (5) (сплошные линии) для различных значений времени. Рис.3. Сопоставление распределений давления в пласте, произведенных с помощью конечно-разностных расчетов (сплошные линии) и аналитического решения (6) (точки) и расчетов с помощью гидродинамического симулятора Eclipse (пунктирные линии), при k = 10-15 м2 и следующих значениях времени t = 1.261⸳105c, 1.261⸳106c, 1.261⸳107c, 2 года. Из рис. 3 видно удовлетворительное согласие кривых, расхождение кривых обусловлено большим шагом по координате x, при уменьшении шага кривые согласуются лучше, но требуется большее время для расчетов. Интересным для практики является случай наличия плохо проницаемой области вблизи скважины, что соответствует загрязнению призабойной зоны пласта парафинами, смолами и т.д. На рис. 4 представлено сопоставление распределений давления вдоль оси x для различных значений размера зоны загрязнения: 0 м (кр. 1), 1 м (кр. 2), 5 м (кр. 3), 10 м (кр. 4), 20 м (кр. 5), значение проницаемости пласта k = 10-13 м2, проницаемость загрязненной области kз = 10-15 м2. О 0.5 I X, км Рис.4. Сопоставление распределения давления в пласте, при наличии загрязненной зоны (сплошные кривые) и при отсутствии загрязненной зоны (пунктирная кривая), при t = 10 дней Как видно из рис. 4. Чем больше загрязненная зона, тем больше отклонение кривой от кривой, не учитывающей загрязнение, так при зоне загрязнения 1 м пунктирная линия и сплошная практически совпадают. Для более глубокого анализа вклада загрязненной зоны в табл. 1 проведено сравнение дебитов для единицы ширины пласта толщиной 8 м для представленных выше случаев, рассчитанных по формуле [4] Н Рк-Р0 At L , L - Lз' к з + и значений средневзвешенного давления, рассчитанных по формуле [4] L P^f Pdx,(8) о для конечно-разностной модели эта формула преобразуется к виду и P=^pf 1=0 Таблица. Сопоставление дебитов для различных размеров загрязненной зоны Размер загрязненной зоны, м 0 1 5 10 20 Максимальное отклонение значений давления от давления «чистого» пласта, Па 0 2.119⸳103 3.215⸳104 1.218⸳105 5.138⸳105 Расстояние от скважины до точки максимального отклонения, м - 426 422 408 396 Дебит, м3/с 1.067⸳10- 5 1.001⸳10- 5 8.020⸳10-6 6.426⸳10-6 4.598⸳10-6 (Qзагр/Qчист)⸳100% 100 95 75 60 43 Р, Па 1.739⸳107 1.739⸳107 1.740⸳107 1.745⸳107 1.764⸳107 Таблица демонстрирует, что чем больше размер загрязненной зоны, тем меньше дебит скважины, так для 20 – метровой зоны дебит отличается от «чистой» скважины на порядок. Уже при 10 – метровой загрязненной области дебит скважины составит только 60% от возможного дебита. На рис. 5 представлена зависимость разности давлений для пласта с загрязненной призабойной зоной и пласта при отсутствии такой области от x для различных значений размера зоны загрязнения: 0 м (кр. 1), 1 м (кр. 2), 5 м (кр. 3), 10 м (кр. 4), 20 м (кр. 5), значение проницаемости пласта k = 1013 м2, проницаемость загрязненной области kз = 10-15 м2. Как видно из рисунка 5 максимальное отклонение давления наблюдается для большей загрязненной области и достигается вдали от скважины при x = 396 м, для других случаев данные приведены в таблице. Рис. 5. Зависимость отклонения давления в модели с учетом загрязнения Pзагр от давления в однородном пласте Pчист от координаты x Итак, разработанная модель позволила установить зависимость дебита скважины от размера загрязненной зоны пласта, несмотря на то, что перепад давления из-за этой зоны значительно увеличивается, дебит падает, это происходит из-за того, что проницаемость в этой области значительно меньше, чем во всем пласте. Представленная в работе конечно-разностная модель позволяет рассмотреть большое количество интересных для практики случаев, ее достоверность подтверждена сравнением с классическим аналитическим решением и результатами моделирования в гидродинамическом симуляторе.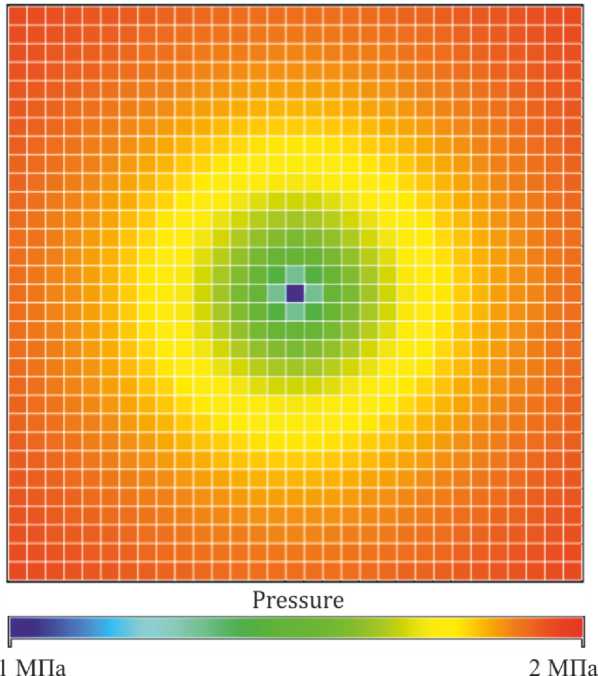
Список литературы Влияние зональной неоднородности коллектора на распределение давления в пласте
- Борисов, Ю.П. Учет неоднородности пласта при проектировании разработки нефтяной залежи / Ю.П. Борисов // Труды ВНИИ, вып. XXI. - 1959. - С. 245-260.
- Валиуллин, Р.А. Математическое моделирование восстановления давления в системе пласт - многоствольная скважина / Р.А. Валиуллин, Р.Ф. Шарафутдинов, М.Ф. Закиров, А.А. Садретдинов, В.Н. Федоров, М.А. Ихсанов // Нефтяное хозяйство. - № 10. - 2010. - С. 104-116.
- Котенёв, А.Ю. Моделирование процесса вытеснения нефти в неоднородных коллекторах / А.Ю. Котенёв, О.Ф. Кондрашев, Р.Ф. Шарафутдинов, А.А. Садретдинов // Электронный научный журнал "Нефтегазовое дело". - № 2. - 2010. - С. 28-32.
- Басниев, К.С. Нефтегазовая гидромеханика: учеб. пособие для вузов / К.С. Басниев, Н.М. Дмитриев, Г.Д. Розенберг. - М.-Ижевск: ИКИ, 2005. - 544 с.
- Бан, А. Об основных уравнениях фильтрации в сжимаемых пористых средах / А. Бан, К.С. Басниев, В.Н. Николаевский // Прикладная механика и техническая физика. - № 3. - 1961. - С. 52-57.
- Ши Д. Численные методы в задачах теплообмена; Пер. с англ. - М.: Мир, 1988. - 544 с.
- Самарский А.А. Теория разностных схем. Учебное пособие, Главная редакция физико-математической литературы изд-ва "Наука", М.: 1977. - 656 с.


