Вложение весовых пространств Соболева в весовые пространства Орлича и в пространство непрерывных функций на анизотропно нерегулярных областях

1.    Введение1.1.    История вопроса

В 1938 г. С. Л. Соболев установил [1], что для областей с условием конуса, при s — 2 + 2 > о,    s е N,    1 < р < q < то                    (1)

Р q пространство Wp(G) вложено в пространство Lq(G) Это утверждение носит название теоремы влоэюения С. Л. Соболева.

В 1980 г. Ю. Г. Решетник перенес [2] результат С.Л. Соболева, о вложении Wp(G) С L_q (G) на области с условием Джона, а в 1983 г. О. В. Бесов - на области с условием гибкого конуса, (см, например, [3]) с теми же ограничениями на. параметры суммируемости и гладкости.

В 2000 г. Килпелайнен и Малы для максимально возможного q установили [4] неравенство Соболева-Пуанкаре для областей с и-условием Джона при s = 1. В 2001 г. О. В. Бесов установил [5] теорему вложения Соболева с максимально возможным показателем q при s Е N для областей с условием гибкого и-конуса. В 2008 г. Б. В. Трушин установил [6] теорему вложения Соболева с максимально возможным показателем q при s Е N для областей с А-анизотропным условием гибкого и-конуса, а в 2010 г. распространил [7] этот результат на. случай пространств со степенными весами. В 2011 г. О. В. Бесов обобщил [8] теорему вложения Соболева с максимально возможным показателем q при s Е N на области с обобщенным А-анизотропный условием гибкого и-конуса.

Более подробную историю вопроса можно найти в недавней монографии [9].

1.2.    Известные результаты о вложении пространства Соболева в пространство Орлича

Хорошо известно, что в предельном случае (если в неравенстве (1) заменить q на то) пространство Wp(G) не вложено в пространство L^ (G). В 1965 г. С. И. Похожаев доказал [10] в случае ограниченной области G с границей, локально удовлетворяющей условию Липшица, вложение пространства Wp(G) в пространство Орлича Lф(G), соответствующее функции Ф(і) = e^|t|P — 1 пр и s = 0. Ранее, в 1961 г., В. И. Юдович получил [11] оценки интегралов типа потенциала, прішодящие к этому вложению.

В 2003 г. Б. В. Трушин установил [12,13] вложение пространства W®(G) в пространство Орлича Lф(G) в передельном случае соответствующей теоремы вложения (в том числе и в случае весовых пространств).

Также следует отметить работы Трудингера [14], Эванса и Эдмундса [15] и Сианчи [16], в которых рассматривались некоторые вопросы, связанные с вложениями в пространства Орлича.

1.3.    Известные результаты о вложении пространства Соболева в пространство непрерывных функций

Если в предельном случае неравенства (1) нестрогое неравенство заменить на строгое, то пространство Соболева вложено в пространство непрерывных функций. Для области с условием конуса это утверждение содержится в монографии [17], а для открытого множества с условием А-рога - в книге [3].

1.4.    Полученные результаты

В настоящей работе устанавливаются теоремы вложения пространства Соболева в пространство Орлича и пространство непрерывных функций для областей с А-анизотропным условием гибкого и-конуса. Результаты распространяются также на случаи вложений весовых пространств Соболева. Тем самым результаты работ [12, 13] переносятся на более общие области, введенные в работах [6,7].

2.    Основные определения и обозначения

Везде далее область G С Rⁿ, G = Rⁿ, n > 2, Q (x, d) = x + (—d, d)ⁿ,

n

А = (А1, А2,..., A_n) G (0, ro)ⁿ,      |А| = V Аг ,      А₀ = min А_г.

^—'              16i6n г=1

При |А| = n, d >  0 А-кубом А-диаметра d называют [6] открытый параллелепипед вида

Q_x (x, d) = x + (—d^x1, d^x1 ) x (—d^x2, d^x2 ) x ... x (— d^x" ,d^x" ) ,

А-длиной вектора x G Rn называют величину

|x|x = max |x«| A» = inf {d : x G Qx(0, d)} . г

При x G G через

•                е - определяют А-расстояіше до границы области G.

Обозначим

Gs = {x G G : dist (x, Rn\G) >5} = 0, где dist(x, Rn\G) = inf{|x — y| : у G Rn\G} - евклидово pace-тояние от точки x G G до границы области G, 5 > 0 достаточно мало.

Пусть у и yxG,d) - характеристические функции соответственно интервала (0,1) и А-куба Qx(0, d). Весовыми будем называть п.в. положительные локально суммируемые функции. Для измеримого множества Е обозначим |Е| = | dx лебегову меру множества Е П G.

EnG

Через р' обозначают показатель, с-спряженный показателю р. то е<-ть —I—‘ = 1.

2.1.    Пространство Соболева

В работе изучается весовое пространство Соболева W®_y._r (G), определяемое [5] как совокупность функций с конечной нормой

||/W^(G)|| = I £ ID“/ILP,V(G)| + ||/IL.(GS)|| \ 'i - при некотором 6 > 0.

2.2.    Пространство Орлича

Вещественную функцию Ф называют N-функцией, если она непрерывна на всей оси, выпукла, четна и удовлетворяет условиям:

lim^C, lim^ = tMG t           t^m t

Весовое пространство Орлича Lф,w (G) с N-функцией Ф определяют [12] как совокупность функций с конечной нормой

II/ Дф,_ш ^(G)|| = inf ¹ Л + [ ^Ф(Т7|№/1) dxA . ч>° У V     Jg             /

Определение 1. Будем говорить, что N-функция Ф принадлежит классу Ne с показателем q > 0, если для некоторого натурального ко > Q-1 найдется последовательность {ак}^=к0 такая, что                   ___ lim к/ак < то, к^^

и справедлива оценка

∞

Ф(t) 6 Е »k\t\^ke.

к=ко

В качестве примера N-функции Ф, принадлежащей классу Ne, в вопросах, связанных с вложениями в пространства Орлича, обычно рассматривают [10,12,13] функцию вида к0-1

Ф(t) = e^|t|e -У -11| ^ке,     ко Е N,      ко >q ^{- 1} .

z—' к!

Но в настоящей работе мы не будем ограничиваться лишь этим случаем.

2.3.    Области с А-анизотропным условием гибкого а-конусаОпределение 2 ( [6]). Пусть область G С R”, о > 1, 0 < t* < 1, к > 0, А = (0, то)”, \А\ = п, Ао >о-1.

Пусть для каждой точки ж Е G существует кусочно гладкий путь

7 : [0,t*] ^G, 7(0) = ж, QA(7(t), KtCT) С G, d7i(t) dt

6 к^-1р\(7 (t))^Ai-A0 для п.в. t Е [0,t*].

Тогда будем говорить, что область G является областью с А-анизотропным условием гибкого о -конуса.

3.    Основные результаты3.1.    Вложение пространства Соболева в пространство Орлича

Теорема 1. Пусть G - область с условием Х-анизотропного гибкого а-конуса, а > Хо — п, b >  0, и выполнены условия

• 1    6 р,г<_ю,    , е N,    Хс — ^п > о,    , + А — ' ^{п + а —}М±1 > 0.

3.2.    Вложение пространства Соболева в пространство непрерывных функций

Р             Хо рг

Тогда для любой N-функции Ф, принадлежаащей классу N_p‘, ко > —, ко > —, имеет место вложение Wp;_y._r (G) С Тф,_ш (G) и справедлива оценка

\\Ф 1Ьф._ш (G)\ 6 С I £ \\D4IL_P,_V (G)П + \\ф L (G_S )\ 1 ,

\ |a|=s/ при to = pX, t = pX и некоторых С, 5 > 0, не зависящих от ф.

Теорема 2. Пусть G - область с условием Х-анизотропного гибкого ст-конуса, а >  Х о — п, b >  0, выполнены условия

• 1    6 р,г< ^,    , е N,    Х о , — п> 0,    , + X —    ■        ■■ > 0,

Р             Хо и имеет место хотя бы одно из неравенств

, _ _п                  ^с(п ± ^{а — Х} о ) ± ¹ , _п

• b > 0    ил и    s= 0.

4.    Некоторые вспомогательные результаты4.1.    Регуляризация А-расстояния

Р

Тогда каждая функция ф е W_p^._r (G) эквивалентна непрерывной на G функции ф и справедлива оценка

ИС(G)П 6 С I £ \D^ILP^(G)П + \ф|Lr(G5)\ I , \ |a|=s/ при t = p^, ) = p^ и некоторых С, 5 > 0, не зависягцих от ф.

Лемма 4.1. [6] Пусть G С Rⁿ, G = R” - произвольное открытое мномсество, Х е (0, то)^п, |Х| = п. Тогда существует такая регуляризация Х-расстояния p\ G СQ^O(G), что для всех х eG

Cipx(x) 6 px (х) 6 C 2 p_A(x),

9px(x') Әхі

6 C 3 px(x)^{1 x}

где константы, с1. с₂. сз зависят лить от размсрности пространства п и параметра, Хо-

4.2. Слабые оценки

интегральных операторов

Рассмотрим оператор

К/ (ж) = j к(ж, у)/(у) dy , ж G G, G где измеримое множество дательная функция.

G С R”, k : G х G ^ R - ядро оператора - измеримая неотри-

Введем при 1 6 р <  q <  то, ж G G, Е С G, у G R”, d >  0

k(ж, у, d) = (1 - ух (ж - у, d)) k(ж, у),

IIlklllG = |||k|||p_{;(/;G = sup sup | k(ж, •, d)v(^)} p lLp (G)|l |Qx (ж,d) | ⁷, $CG d>0

где v - некоторая весовая функция.

Лемма 4.2. [7]. Пусть область G С R”, 1 6 р < q <  то, v - весовая функция. Тогда для интегрального оператора К с ядром k существует постоянная С >  0, зависящая лишь от размерности п, такая, что справедлива оценка слабого типа

1                          7

sup у |{ж G G : ч>0

|К/(ж)| >у}|⁷ 6 С р- -        ||k|||G Н/ IL_P^ (G)H.

4.3.    Сильные оценки интегральных операторов

Лемма 4.3. Пусть область G С R”, 1 6 р < то, v - весовая функция, а для интегрального оператора К с яд}юм k при всех q > р справедлива оценка

111 k 111G = 111 k II U,;G 6Cq« для некоторых С > 0 и 3 > 0. пс зависящих от q. Тогда имеет место оценка сильного типа

НК/ L(G) Н 6 Ci max j 1,----^ I q Н/|Lp,_v(G) Н,

(q - р) 7

где Ci пс зависит от q.

В работе [13] доказан изотропный аналог данного утверждения. Его доказательство базируется на изотропном аналоге леммы 4.2 (см. [18-20]), и поэтому дословно переносится на анизотропный случай леммы 4.3.

4.4.    Интегральные оценки функций через производные

Лемма 4.4. [7]. Пусть область G С R”.

е G (0,1), R > 0,      C > 1, А G (0, то)”, |А| = п,

7 : [0, Д] ^ G - кусочно гладкий путь, г : [0, Д] ^ (0, то) - непрерывная кусочно гладкая функция со свойствами

⁰<  43) ^{6 e}px⁽7^(t)),

(r(t)^Xo^ 6 C для п.в. t G [0,3_Ж],

r(t_x) >  е²,

и

7(0)=ж,    рх(7(t_x )) > е, t_x 6 R,   ,7‘(t)| 6 C для п.в. t G [0,3_Ж].

Тогда для почти всех ж G G справедлива оценка

|/(ж)| 6 С Аі

У |Da/ | I (ж) + СА2 I у |Da/ | I (ж) + САа/(ж), H=s        /               \|a|=s        / где С не зависит от /. ж. и

Аід (ж)

r (0) ^x 0

Z ^r1

п ^х 0

j д (у) dy dt, Qx^,t У)

tx

А2д (ж)

s— 1

о

r (t) ^п j      д (у) dydt,

ОлЫРжр))

А а /(ж)

j ^|/ Ы^у.

Qx (l(tx),r(tx))

Запишем операторы Аг в виде

Аід(ж) = j ki(ж,у)д(у)dу,     г = 1, 2, 3.

G

Лемма 4.5. [7] Пусть G - области с условием A-анизотропного гибкого а-конуса. весовая функция ж(ж) = р а (ж)“, и выполнены условия

1 6 р,г < то,

s G N,

^A o ^s

—

п

- >  0. Р

Тогда имеют место оценки

\\ki (ж, -,d)v(-) p |Tp‘(G)H 6 Сіх

(7(0)) ^{Рх(ж) Pn} 1 ^(ж,d),

где

п 1 (ж, d) = <

1 (- ) ^p r(0)^A 0 ^{s - п}

при Aos--= 0, при Aos--> 0, Р

(tx j X

о

(

d

Са max{r(0), t^x o }

)x

/             , \ (s—1)p‘                xp ‘                 ap' \ p‘ x ^t + r (0)A0J        r (t) 0 ^p рд(д(t)) p dt j ,

һк а (ж, •,d)|Lr' (G)H 6 С 4

Z ( ^{(1 —} x a ^{(ж —} y^,d))x ( ^|ж с₅^{У | л} )) ^dy )

Gs                                               )

при некоторых С >  0. нс зависяіцих от ж и d.

5.    Оценки норм операторов А^ из леммы 4.45.1.    Оценка нормы оператора А1

Лемма 5.1. Пусть G - область с условием X-анизотропного гибкого с-конуса, а >  Х о — п, b >  0, и выполнены условия

1 6 Р < ^о,      з G N,      Хоз — — > 0,      Хоз + b —----- > 0.

Р                   р

Тогда для всех конечных q > р справедлива оценка

|II ^^i ||| _G = ||| wki ||| p_№q;G 6 Cq^p,

Р =

р 0

при Хоз —   = 0, при Хоз--> 0

при ш = рьх, и = рХ и некотором С, не зависящем от функции g и показателя q.

Доказательство. Из леммы 4.5 имеем

( d \       _а                — —

—— px(x) ^p"i(x,d)px(x) d ⁹ г(⁰)

til ^

6 С₂ sup sup dq n₁(x,d')p_x(x)^b" xEG 0

где

п1(х, d) = <	⎧ 1 [ (ь ^ ) р r(0)x 0 s_—	при Хоз — при Хоз —	п - = 0, Р п - >  0.
			Р

Воспользуемся тем, что

(^)

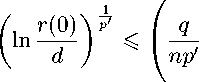
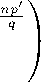
р’

„ 1  ^(0)

= ^C 3 ^qр (мД

Поэтому при Х о з —

— = 0 имеем Р

|||wfc i ||| g 6 C4q^р’

b_а sup sup px(x) р 6 C4qр’.

x E G о<и,6г(о)

Если же Хоз--> 0. то Р

|||wfc i |||G 6 C 5 sup sup px(x)^x 0 ^s+b x e g о<а,6т(о)

-

—+а

— 6C 5 .

5.2. Оценка нормы оператора А2

Лемма 5.2. Пусть G - область с условием Х-анизотропного гибкого н-конуса, а > Хо — п, b > 0, и выполнены условия

1 6 Р< о,    з G N ,    Х о з — ^П > 0,    з + Д — Д" ^{+ а — Х о ) + 1} > 0.

Р             Х о           р

Тогда для всех конечных q >  р справедлива оценка

111 W^2 111 G = 111 W^2 111 p,x;q;G 6 Cq^P ,

( 1 при Ь = 0, s - А" + ° — А°) ± 1 =0, в = Р                     ( Р „ п         к п         ст(п + ° — А°) + 1 V п

0 при Ь >  0 ил и s --= 0

р при w = рХ, v = рХ и некотором С, не зависящем от функции g и показателя q.

Доказательство. В работе [7] показано, что для области с А-анизотропным условием гибкого и-конуса можно так «исправить» кусочно гладкий путь у в определении 2, что условия теоремы 4.4 будут верны с функцией r пропорциональной регуляризованному А-расстоянию рх. Поэтому, в силу леммы 4.1, справедливы оценки рхЫі) >   .

r(t) = срх(у (t)) >  СС1Рх(у (t)) >  CC1Kt^CT = c°t^CT,

Из леммы 4.5 имеем

IIIWI g 6 С1 sup sup x E G d>°

b

(р_х(х)^х° + d^x^ ^A° d ?

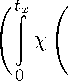
d

C2 max{r(0), t A° }

)

X

/             , \ (s—1)p'                 \p ‘                  ap'    \ ^p'

X \t + r (0)^X°J        r (tp °   ^^p р_х(у (t))    ^p dt\   .

Тогда при a >  А° — п, Ь >  0 получаем k₂G 6 С3 sup sup(I1 (x, d) + I₂(x , d)), где xEG d>°

Ii(x, d) = r(0)^+ 9

Tx

I -(..-0)) °

\ P7

r(0)((s—     У?-" )Pdt

I2(x,d)= (рх(x)x° + dx° j ■" + ,"•

1 tx                                                              p'

I x -4т) ■ ■ ¹⁺ (^-p^-^ ) p ' dt I J    \ C_bt^°)

Tx

(t,,rr}.

Ho

Ii(x,d) 6 Cer(0)^{b+ 9 +(s—1)х}°⁺ ^^{Q-p— +} T- = Сб-(0)^х° ^s+b— ^ 6 Сб < Сб

.      , п + a при A°s + Ь-- Р

> 0.

Заметим, что (п + a — А°)(сА° — 1) > 0 ил и а(п + a — А°) + 1 >

п + a

А°

откуда

A₀s + Ь —П±Л ₌а₀ (s + А — ПД1 >А° (sA — ^ІП + ^—УіІ + ІА > 0. Р             А°    А°р / V А°           р        /

I₂(x,d) = 0 щ )іі r(0)^x° > 2Ct_x. а. при т_х

_ЕсліІ s — ^⁽ⁿ±^az2°⁾±l >  0, _то р

г(0)х°

2C

< t_x имеем следующее.

s+ ф — Л⁽Л±^а-Ао)+1 + П             , _{b CT}(„_+a-A°) + 1

I2(x,d) 6C₇t_x ^°      ^{p      x}°^q 6С7^⁵ ^°      p

< С7.

Если s -        ^{; A}< 0. то

р

І 2 (х, d) 6 С8Х

_d \    /   - ( п + а—^Ж    ^

^ J \         ^P / ^q

1 ^dX

_x , I b ^ ( n + a^-A 0) + 1

6 C 8 C₅^Xo R^s+M p

< C9 .

при _s + 1 - £(n±a-A o 2±l > 0. A o            р

Если s - '   ±             = 0 ii b = 0. to

P

i n / ('О'’'0! \ P‘ l2(x,d) 6Ciod^ hn -5^

n

6 Cwd^

′

/        \ ⁿP

Xoq / C ' \ ^Xoq нр’   d'

P‘

= Ciiq^p‘ ,

где d_x = max <^d, C₅tX‘' }.

Если s -       ^{; A} = о 11 b >  0

TO

P

І 2 (х, d) 6 Ciod^b_x

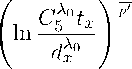
. / i / c^Xot \^bp \ ^P

' | bp ¹       '  )   "^

5.3.    Оценка нормы оператора М3

Лемма 5.3. Пусть G - область с условием X-анизотропного гибкого а-конуса, b >  0, 1 6 т < то, s Е N. Тогда для вс еж конечных q > т справедлива оценка

IІҺ^зІІІС = ||Һ^з|||г,И;7;С 6 C, при ш = д', и = 1 и некотором C, не зависягрем от функции g и показателя q.

Доказательство. Из леммы 4.5 имеем

111 ш^3111G 6

,                                                                                                                1

6 C1 sup sup xEG d>0

Z ( ^{(1 -} Xx ⁽Ж ^- y^,d))x ( ^1Ж -^ ' )) ^dy I px⁽x^{)i>dn 6} G_S

6 C 1 supsupX Ur) (d^nr‘A¹’ px(x)^bdⁿ = C 1 supx      d"^+b = C 1 C”^+d.

xEGd>0 ^C22/ V z                 d>0 ^C22/

6.    Доказательство основных результатов6.1.    Доказательство теоремы 1

Из леммы 4.4 следует, что для почти всех х Е G справедлива оценка

|ш⁽ж)/⁽х)| ⁶

6 C i w(x)M i I ^2 I^“/1 I (х) ±C i w(x)A 2 I ^2 I^“/1 I (х) ±C i w(x)M 3 /(х). \ |^ | = s        )                          \|a | = s         /

Поэтому из леммы 4.3 для всех к > ко, в силу лемм 5.1, 5.2 и 5.3, получаем

ІИ lL_kp, (G)| 6 С₂(кр')р’ ||f W,, (G)|.

Условие

Ao„ + 6 - 2±a > о p леммы 5.1 выполнено в силу справедливости оценки (2).

Оценим теперь при фиксированном , > 0 интеграл j" Ф(,|ш/|)dx для некоторой N- (])упкпіш Ф. прішадлежаіцей классу N_p‘:

Z Ф(,|ш/1) dx 6 2 а_к Z \w/\^кр'dx 6

6 52 ai,^kp‘ ( C2(kp‘)p1‘ |/ \W_p,_vr (G)| ) ^lp k=ko

.

′1

Обозначим для удобства F = С₂р ^р‘ ||/|W_{p(G)|, тогда}

∞

Ф(,И1) dx 6 ^ a_kk^k(,F)^kp‘ .

Получили степенной ряд по (,F)^p . Его радиус сходимости

R =     ----> 0.

lim к кfak k^^

R р’ Выберем произвольно Ri < R и возьмем , = пғ = ---. Тогда

F

Z Ф(,_ғ|w/1) dx 6 52 °kk^kRi = С3. ^G                  k=k₀

Поэтому

||f Дф,_№ ^(G)|\ = inf¹ (1± [ Ф;у ^w/ \)dx\ ч>⁰, V Jg            /

6 ^(l + j Ф(^^\w/\)dx^ 6

6 ^C3^F = C4F = С5|/|Wp,,_;r(G)|. R р’

Тем самым доказано утверждение теоремы

6.2. Доказательство теоремы 2

Пусть ж G G, Е = dist($, ЭС). Тогда / G W_p ^ (^Ж, D)' "° ^{классическ}°й теореме вложения Соболева (см., например, [17]) функция / в шаре В (ж, -) эквивалентна непрерывной функции. Значит, она эквивалентна непрерывной функции и на всей области G.

Для всех q >  р ± 1 из лемм 5.1, 5.2 и 5.3 имеем

|w/ L (G)| 6С1|/ \W_p,._r (G)|.

Теперь утверждение теоремы 2 следует из очевидного соотношения l|g|L»(G)|| 6 lim \\g\Lq(G)W. q^^

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект 11-01-0074), гранта Президента РФ «Ведущие научные школы» (проект НШ-65772.2010.1), ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы (контракты 16.740.11.0128, 16.740.11.0568).