Внеконтактная деформация при реверсивном поверхностном пластическом деформировании

jiiiiiHHOiiiaiii

Состоянию поверхностного слоя деталей машин уделяется должное внимание как на стадии их изготовления, так и в процессе эксплуатации машин и оборудования. Все проблемы, связанные с надежностью изделий машиностроения, во многом зависят именно от качества поверхностного слоя деталей машин [1–3]. Улучшить состояние внешнего слоя деталей и элементов конструкций удается достаточно эффективно при использовании после механической обработки резанием отделочно-упрочняющей обработки поверхностным пластическим деформированием (ППД). Благодаря ППД можно не только сгладить микронеровности поверхности, но и повысить твердость поверхностного слоя и сформировать в нем сжимающие остаточные напряжения. Всё это благоприятно сказывается на работоспособности деталей машин и изделий машиностроения в целом [4–6].

При ППД, в отличие от обработки резанием, металл не удаляется путем отрыва стружки, а перераспределяется под действием давления в тонком поверхностном слое. Деформирующий инструмент в виде шарика или ролика в зоне контакта с заготовкой воздействует на металл, сдавливая его в направлении, перпендикулярном обрабатываемой поверхности. При этом часть деформируемого материала выдавливается на свободную поверхность заготовки, образуя вокруг рабочего ин- струмента упругопластический наплыв, называемый технологами «волной», которая характеризуется двумя основными геометрическими параметрами: высотой и длиной. При использовании известных статических методов ППД размер упругопластической волны перед деформирующим инструментом значительно больше, чем после, и в направлении продольной подачи размеры волны значительно выше, чем в направлении главного движения [7–9].

Подъем металла в виде упругопластической волны увеличивает площадь контакта рабочего инструмента с обрабатываемой поверхностью, что оказывает существенное влияние на силу трения, температуру в зоне деформации, ухудшает доступ смазочно-охлаждающей жидкости в зону обработки [10–12]. Если в очаге деформации возникают в основном сжимающие напряжения, то в упругопластической волне, которая формируется на поверхностном слое, возникают растягивающие напряжения, которые при большой интенсивности могут являться источником зарождения повреждений в виде микротрещин [13–15].

В фундаментальной монографии профессора В.М. Смелянского [16] показано, что именно в вершине упругопластической волны происходит ужесточение схемы напряженного состояния, снижение запаса пластичности, которые приводят к разрушению поверхностного слоя. Таким образом, волнообразование при ППД приводит к формированию дефектного слоя, кото- рый снижает глубину упрочнения и повышает интенсивность накопленной деформации. Экспериментально доказано, что подавление или механическое удаление упругопластической волны повышает качество поверхностного слоя [17; 18].

В связи с вышеизложенным вопрос о влиянии ППД на процесс образования упругопластической волны является весьма актуальным при изготовлении деталей машин с обеспечением качественного поверхностного слоя. Изучение процесса волнообразования при ППД относится к достаточно сложной технической задаче, так как экспериментально определить ее можно только качественно или весьма приближенно. Внедрение в исследовательскую практику программных средств на основе конечно-элементного моделирования позволяет получить достаточно надежные численные результаты.

Авторами статьи предложен новый способ поверхностного пластического деформирования, основанный на реверсивном движении рабочего инструмента [19]. Способ направлен на решение задачи по интенсификации напряженного состояния в очаге деформации и остаточных напряжений в упрочненном слое.

Цель данной работы заключается в определении геометрических параметров упругопластической волны и напряженного состояния в ней в зависимости от основных технологических параметров реверсивного поверхностного пластического деформирования.

1.    Способ реверсивного поверхностного пластического деформирования

Новый способ ППД поясняется на рис. 1, где показаны конструкция и кинематика рабочего инструмента, реализующие предлагаемый способ реверсивного поверхностного пластического деформирования цилиндрических деталей.

Особенность данного способа заключается в том, что рабочий тороидальный инструмент выполнен в виде двух деформирующих роликов, расположенных относительно направления подачи под некоторым углом α н , при этом ось вращения рабочего инструмента (РИ) расположена параллельно оси заготовки, а рабочему инструменту сообщают реверсивное вращение относительно оси, проходящей через плоскость, соединяющую два деформирующих ролика и перпендикулярную оси заготовки, с амплитудой угла ± α р [19]. Вершины деформирующих роликов располагаются относительно друг друга на расстоянии I .

Как видно из схемы обработки (см. рис. 1) параметрами режима, определяющими кинематику процесса являются: частота вращения заготовки (nз), продольная подача (Sпp), радиальный натяг (t), реверсивная частота вращения рабочего инструмента (nр), начальный угол установки (αн) и амплитуда угла реверсивного вращения РИ (αр). Заготовку 3 закрепляют в трехкулачковом патроне 1 токарно-винторезного станка и поджимают вращающимся центром задней бабки 2. Заготовке придают вращательное движение с частотой nз (об./мин). Рабочему инструменту 4 одновременно сообщают продольную подачу Sпр и реверсивное вращение nр вокруг своей оси.

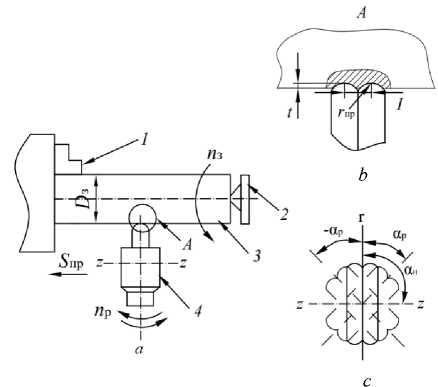
Рис. 1. Схемы реверсивного ППД двухрадиусным роликом ( а ), его рабочей зоны ( b ) и реверсивного вращения ( c ): 1 – трехкулачковый патрон; 2 – задняя бабка; 3 – заготовка;

4 – рабочий инструмент

Fig. 1. Schemes of reversible PPD with a two–radius roller ( a ), its working area ( b ) and reverse rotation ( c ): 1 – three–cam chuck;

2 – tailstock; 3 – blank; 4 – working tool

Под воздействием двухрадиусного тороидального инструмента во внеконтактной зоне деформации образуются пластические наплывы – волны (рис. 2), которые характеризуются двумя основными геометрическими параметрами: высотой h и длиной волны l.

На рис. 2 показаны формы упругопластических волн в направлении продольной подачи ( А 1 ) и в направлении главного движения ( А 2 ). Следует отметить, что под воздействием двухрадиусного ролика упругопластические волны, образующиеся в результате реверсивного ППД, обладают характерной конфигурацией. В направлении главного движения вокруг рабочего инструмента создаются упругопластические волны ( А 2 ), обладающие практические одинаковой формой и размерами. При этом в направлении продольной подачи упругопластические волны ( А 1 ), образующиеся в зоне, обработанной и необработанной поверхностей, имеют разные геометрии и отличаются от упругопластических волн ( А 2 ) большими размерами высоты h 1 и длины l 1 . Это объясняется не только наличием продольной подачи, но и ориентацией РИ при ППД. Длины упругопластических волн ( l 1 и l 2 ) определяли от точки пересечения РИ с упругопластической волной до точки пересечения упругопластической волны с горизонтальной линией (для l 1 ) и с окружностью детали (для l 2 ), а высоты упругопластических волн ( h 1 и h 2 ) определяли от вершины упругопластической волны до горизонтальной линии (для h 1 ) и до точки контакта упругопластической волны с окружностью детали (для h 2 ) (см. рис. 2).

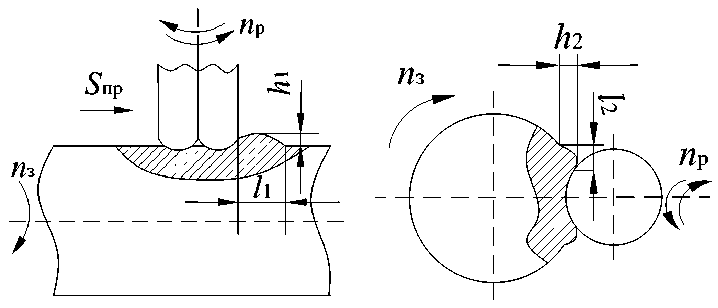
Рис. 2. Форма упругопластических волн при реверсивном

ППД: а – в направлении продольной подачи ( А 1 );

b – в направлении главного движения ( А 2 )

Fig. 2. The shape of elastoplastic waves during reverse PPD: a – in the direction longitudinal feed ( A 1 ); b – in the direction of the main movement ( A 2 )

2.    Конечно-элементное моделирование процесса обработки реверсивным ППД

В настоящее время существуют разнообразные численные методы для расчета напряжений, в которых широко и эффективно используется метод конечных элементов (МКЭ) [20–22]. Метод конечных элементов решает эти задачи, используя дифференциальные уравнения, создавая сетки конечных элементов, связанных друг с другом узлами, для того чтобы заменить обычную физическую модель математической моделью, покрытой сеткой, позволяющей наиболее точно рассчитать напряжения, деформации, смещения и т.д. в рассматриваемом положении объекта. Для расчета напряжений посредством МКЭ часто используют программное обеспечение, среди которых программный пакет ANSYS может полностью решать проблемы в рамках решаемых задач, упомянутых выше [23–25].

На рис. 3 показана конечно-элементная модель реверсивного ППД двухрадиусным роликом. Параметры моделирования: конечно-элементная форма – треугольная форма для рабочего инструмента и тетраэдрическая форма для заготовки (рис. 3, а ), сгущение 137 613 элементов, 43 916 узлов. Условия контакта: в данной работе выбрали контакт типа Frictional (трение), контактную (заготовка) и целевую (рабочий инструмент) поверхности; коэффициент трения в зоне контакта рабочего инструмента с поверхностью заготовки f = 0,1. Граничное условие: в нашем случае рабочему инструменту одновременно сообщают продольную подачу S пр и реверсивное вращение n р вокруг своей оси, а также прижатие к вращающейся обрабатываемой заготовке. Заготовка крепится в двух точках на концах и вращается вокруг своей оси О z . Поэтому принят запрет всех перемещений ( Translation X , Y , Z – Fixed ) и вращение по оси О z ( Rotations – Free Z ) при назначении частоты вращения заготовки. Аналогичны граничные условия для рабочего инструмента ( Translation Y – Free )

для назначения радиального натяга рабочего инструмента; ( Translation Z – Free ) для назначения величины продольной подачи; ( Translation X – Fixed ); ( Rotations Y – Free ) для назначения реверсивной частоты вращения рабочего инструмента (рис. 3, b , c ).

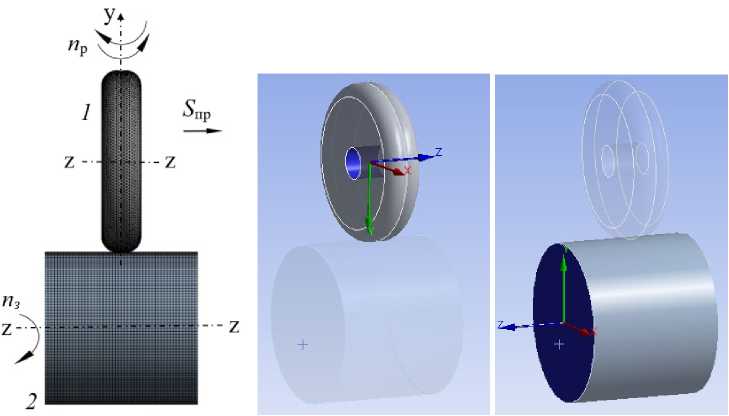
b

Рис. 3. Конечно-элементная модель реверсивного ППД двухрадиусным роликом ( а ), граничные условия для рабочего инструмента ( b ) и заготовки ( c ); 1 – двухрадиусный ролик;

2 – цилиндрический образец

Fig. 3. Finite-element model of a reversible PPD with a two-radius roller ( а ), boundary conditions for the working tool ( b ) and workpiece ( c ); 1 – a two-radius roller; 2 – a cylindrical sample

Для исследования влияния основных параметров реверсивного поверхностного пластического деформирования на размеры упругопластической волны рассмотрены 6 параметров – продольная подача ( S пр ), частота вращения заготовки ( n з ), радиальный натяг ( t ), реверсивная частота вращения РИ ( n р ), начальный угол установки РИ (α н ) и амплитуда угла реверсивного вращения РИ (α р ). Для проведения расчетов по определению размеров упругопластической волны приняты следующие параметры и режимы обработки: тип рабочего инструмента – двухрадиусный ролик со следующими переменными значениями: реверсивная частота вращения двухрадиусного ролика n р = 60...360 дв.ход./мин, начальный угол установки РИ α н = 0...180 ⁰ , амплитуда угла реверсивного вращения двухрадиусного ролика α р = ± 15...± 60 ⁰ , продольная подача S пр = 0,1...0,6 мм/об, частота вращения заготовки n з = 60...300 мин ^-1 , натяг t = 0,1...0,9 мм. Диаметр ролика D и = 30 мм; профильный радиус r пр = 2,5 мм; материал – твердый сплав ВК8; модуль упругости Е = 6·10 ⁵ МПа; коэффициент Пуассона μ = 0,3; коэффициент трения в зоне контакта рабочего инструмента с поверхностью цилиндра f = 0,1.

Характеристики заготовки: в качестве заготовки был использован цилиндр диаметром D з = 20 мм; материал – сталь 45 – упругопластический, упрочняющийся; модуль упругости E = 2·10 ⁵ МПа; коэффициент Пуассона μ = 0,3; диаграмма деформирования материала – билинейная (предел текучести σ т = 360 МПа, модуль упрочнения E Т = 6,8·10 ³ МПа).

3.    Результаты компьютерного моделирования 3.1.    Влияние параметров ППД на размеры упругопластических волн

Рассмотрим влияние продольной подачи, натяга, частоты вращения заготовки, реверсивной частоты вращения РИ, начального угла установки РИ и амплитуды угла реверсивного вращения РИ на размеры упругопластической волны при реверсивном ППД. Базовые режимы обработки представлены в табл. 1.

Таблица 1

Базовые режимы реверсивного ППД

Table 1

Basic modes of reverse PPD

n р (дв. ход./мин)	α н (град)	α р (град)	t (мм)	n з (мин-1)	S пр (мм/об.)
180	90	± 45	0,5	100	0,2

Следует отметить, что для выявления закономерности изменения геометрических размеров упругопластических волн, образующихся при внеконтактной деформации, а также определения их напряженного состояния была выбрана несколько завышенная величина радиального натяга ( t = 0,5 мм), которая в производственной практике применяется весьма редко. Расчетная завышенная величина натяга позволит также обосновать его реальное значение, которое используется на практике.

На рис. 4 представлены зависимости размеров упругопластических волн от продольной подачи РИ.

Из рис. 4 видно, что с изменением величины продольной подачи РИ в основном изменяются размеры только упругопластических волн в направлении продольной подачи. При этом с повышением продольной подачи РИ от 0,1 до 0,4 мм/об. значения размеров упругопластических волн ( А 1 ) существенно увеличиваются, а свыше 0,4 мм/об. – практически не изменяются. Величина продольной подачи РИ оказывает весьма слабое влияние на изменение размеров упругопластических волн в направлении главного движения ( А 2 ).

На рис. 5 показаны зависимости размеров упругопластических волн от величины радиального натяга.

Из рис. 5 наглядно видно, что при всех значениях величины радиального натяга ( t ) упругопластическая волна, образующая в направлении продольной подачи ( А 1 ), имеет больше длину и высоту, чем в направлении главного движения ( А 2 ) по следующим соотношениям: l 1 = (1,2…1,4) l 2 ; h 1 = (1,6…1,8) h 2 . С увеличением величины радиального натяга ( t = 0,1 – 0,4 мм) линейные размеры упругопластических волн увеличиваются благодаря непрерывному накоплению деформации с повышением напряженного состояния поверхностного слоя, при этом запас пластичности металла постепенно снижается.

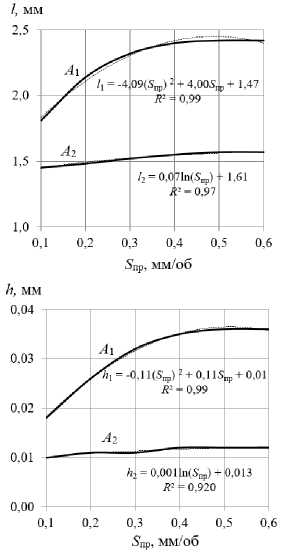
Рис. 4. Влияние продольной подачи рабочего инструмента на размеры волн: А 1 – в направлении продольной подачи;

А 2 – в направлении главного движения

• Fig. 4.    Influence of the longitudinal feed of the working tool on the size of the waves: A 1 – in the direction of the longitudinal feed; A 2 – in the direction of the main movement

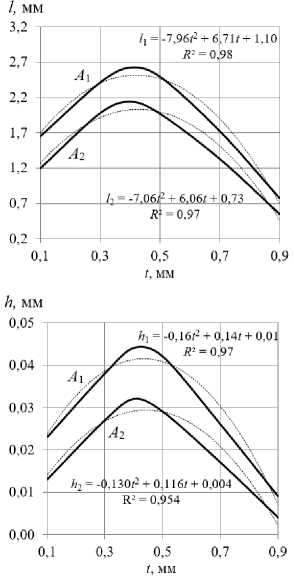
Рис. 5. Влияние величины радиального натяга на размеры упругопластических волн: А 1 – в направлении продольной подачи; А 2 – в направлении главного движения

• Fig. 5.    Influence of the value of the radial interference on the dimensions of elastic-plastic waves: A 1 – in the direction of the longitudinal feed; A 2 – in the direction of the main movement

При t = 0,4 мм линейные размеры упругопластических волн достигают максимального значения. С дальнейшим увеличением величины натяга ( t ) размеры упругопластической волны снижаются. В технологической практике при большой величине радиального натяга в результате охрупчивания и отслаивания упрочненного металла происходит «шелушение» поверхностного слоя.

На рис. 6 представлены зависимости размеров упругопластических волн от частоты вращения заготовки.

По рис. 6 можно отметить, что с увеличением частоты вращения заготовки от 60 до 180 об/мин наблюдается рост размеров упругопластических волн в направлении продольной подачи, а при частоте свыше 180 об/мин размеры упругопластических волн практически не изменяются. Изменение частоты вращения заготовки оказывает незначительное влияние на размеры упругопластических волн в направлении главного движения.

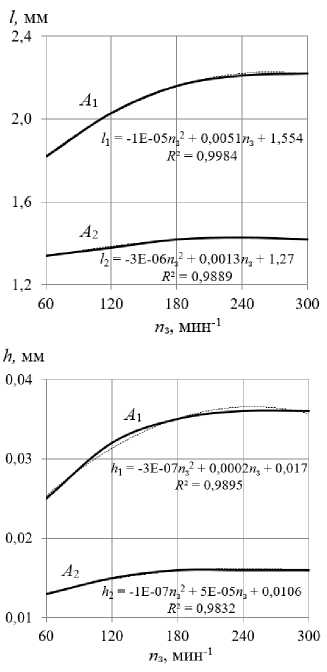
Рис. 6. Влияние частоты вращения заготовки на размеры упругопластических волн: А1 - в направлении продольной подачи; А2 - в направлении главного движения

• Fig. 6.    Influence of the workpiece rotation frequency on the

dimensions of elastic-plastic waves: A 1 - in the direction of the longitudinal feed; A 2 - in the direction of the main movement

На рис. 7 представлены зависимости размеров упругопластических волн от реверсивной частоты вращения РИ. Закономерности изменения размеров упру- гопластических волн качественно совпадают с таковыми на рис. 6.

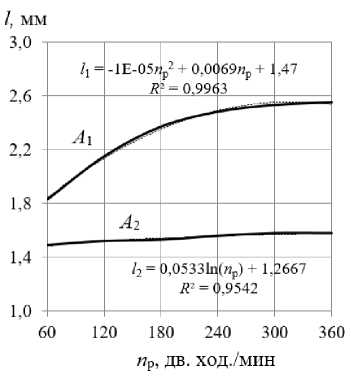
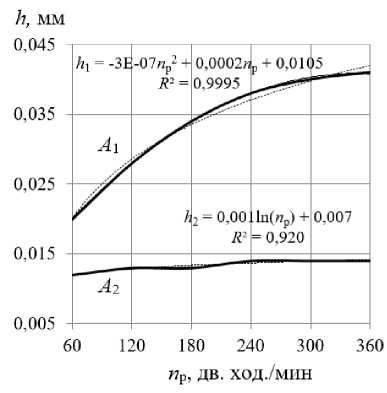
Рис. 7. Влияние реверсивной частоты рабочего инструмента на размеры упругопластических волн: А 1 - в направлении продольной подачи; А 2 - в направлении главного движения

• Fig. 7.    Influence of the reverse frequency of the working tool on the size of elastic-plastic waves: A 1 - in the direction of the longitudinal feed; A 2 - in the direction of the main movement

На рис. 8 показаны зависимости размеров упругопластических волн от начального угла установки РИ.

Из рис. 8 видно, что при ан = 90°, т.е. когда ось вращения РИ расположена параллельно оси вращения заготовки, размер упругопластических волн достигает своего максимального значения в направлении продольной подачи (А1) и минимального значения в направлении главного движения (А2). С увеличением начального угла установки РИ от 0° до 90° значения размеров упругопластических волн в направлении продольной подачи (А1) увеличиваются, а в направлении главного движения (А2) уменьшаются. Но при увеличении начального угла установки инструмента от 90° до 180° установленные закономерности изменяются на обратные. Следует отметить, что степень изменения размеров упругопластических волн в направлении глав- ного движения (А2) меньше, чем степень изменения размеров упругопластических волн в направлении продольной подачи (А1).

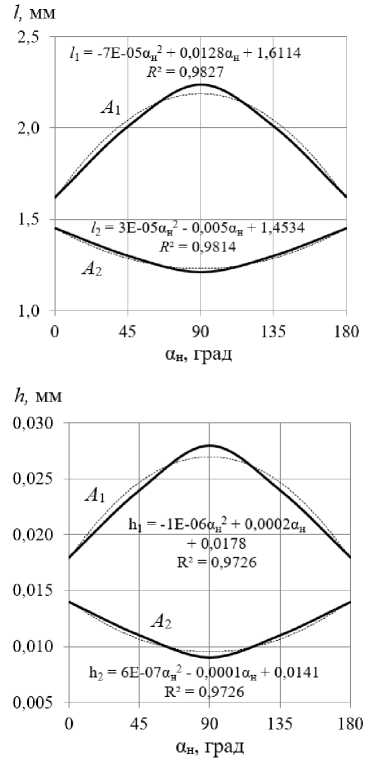
Рис. 8. Влияние начального угла установки рабочего инструмента на размеры упругопластических волн при: А 1 - в направлении продольной подачи; А 2 - в направлении главного движения

• Fig. 8.    Influence of the initial installation angle of the working tool on the dimensions of elastic-plastic waves at: A 1 - in the direction of the longitudinal feed; A 2 - in the direction of the main movement

На рис. 9 показаны зависимости размеров упругопластических волн от величины амплитуды угла реверсивного вращения РИ при ППД.

Из рис. 9 следует, что с увеличением α р от ± 15 до ±45 град. значения размеров упругопластических волн в направлении продольной подачи ( А 1 ) и в направлении главного движения ( А ₂ ) увеличиваются. С дальнейшим увеличением амплитуды угла вращения РИ длина и высота волн в двух направлениях практически не изменяются. Степень изменения размеров упругопластических волн в направлении главного движения ( А ₂ ) меньше, чем таковая в направлении продольной подачи ( А 1 ).

Таким образом, результаты исследования показали, что основные параметры реверсивного ППД значительно влияют на размеры упругопластических волн. Для минимизации размеров упругопластической волны ре- комендуется назначать рациональные режимы обработки реверсивным ППД: продольная подача 0,1…0,2 мм/об., натяг 0,1…0,15 мм, частота вращения заготовки 60…120 об/мин, реверсивная частота вращения рабочего инструмента 60…80 дв.ход./мин, начальный угол установки РИ 0…30 град. или 150…180 град., амплитуда угла реверсивного вращения РИ ± 15…± 20 град.

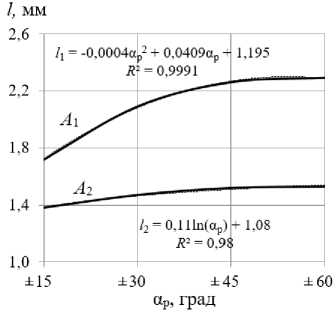
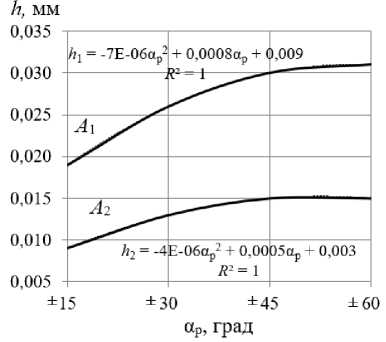
Рис. 9. Влияние амплитуды угла реверсивного вращения рабочего инструмента на размеры упругопластических волн: А 1 - в направлении продольной подачи; А 2 - в направлении главного движения

• Fig. 9.    Influence of the amplitude of the angle of reverse rotation of the working tool on the dimensions of elastic-plastic waves: A 1 - in the direction of the longitudinal feed; A 2 - in the direction of the main movement

• 3.2.    Влияние физико-механических свойств материала на размеры упругопластических волн

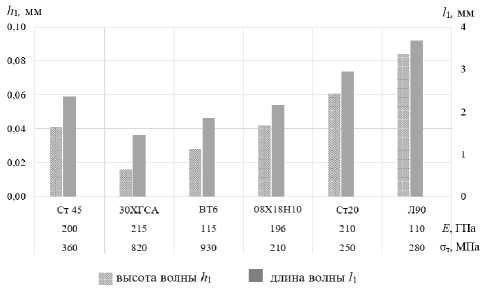
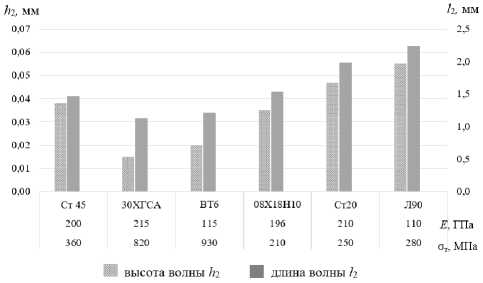
Из технологической практики известно, что чем пластичнее металл, тем большую степень деформации он позволяет обеспечить. С высокой степенью вероятности это справедливо и для внеконтактных деформаций. Для количественного определения влияния физико-механических свойств материала на размеры упругопластических волн после реверсивного ППД выполнены расчеты для некоторых черных металлов и цветных сплавов (рис. 10). Следует отметить, что при реверсивном ППД с базовыми режимами обработки превышение размеров упругопластических волн в направлении подачи (А1) по сравнению с размерами упругопластических волн в направлении главного движения (А2) справедливо не только для сталей, но и для некоторых цветных сплавов.

b

Рис. 10. Влияние физико-механических свойств металлов на размеры упругопластических волн при реверсивном ППД: а – в направлении продольной подачи ( А 1 ); b – в направлении главного движения ( А 2 )

Fig. 10. Influence of physical and mechanical properties of metals on the sizes of elastoplastic waves during reverse SPD: a – in the direction of the longitudinal feed ( A 1 ); b – in the direction of the main movement ( A 2 )

Из рис. 10 видно, что физико-механические свойства металла значительно влияют на размеры упругопластических волн внеконтактной деформации при реверсивном ППД. Большие размеры упругопластических волн наблюдаются у материалов, имеющих низкий предел текучести (латунь Л90, сталь 20). Повышение модуля упругости приводит к снижению линейных размеров упругопластических волн при реверсивном ППД. Также установлено, что чем выше предел текучести материала, тем ниже размеры упругопластических волн.

Максимальные размеры упругопластических волн формируются при обработке медного сплава Л90, минимальные образуются при упрочнении стали 30ХГСА. Полученные результаты моделирования позволяют описать соотношение высоты упругопластических волн от физико - механических свойств металлов в направлении продольной подачи:

h1 = (0,74…0,76).10-3 E, h1 = (0,22…0,25).10-3 σT, где единицы измерения Е – ГПа, σT – МПа, а h1 – мм.

4.    Напряженное состояние в упругопластической волне

Кроме деформированного состояния упругопластических волн, которое зависит от основных параметров реверсивного ППД, напряженное состояние упругопластических волн в зоне внеконтактной деформации является тоже немаловажной информацией для оценки качества обработанной поверхности ППД. При реверсивном ППД двухрадиусным роликом в очаге деформации возникают временные, а в упрочненных поверхностных слоях цилиндрических деталей остаточные напряжения, которые являются одним из основных показателей качества поверхностного слоя. При этом временные напряжения возникают при постоянном воздействии внешних сил в зоне деформации, а остаточные напряжения остаются в деталях после прекращения их действия [26–27]. Временные напряжения оказывают влияние на энергосиловые характеристики процесса и глубину упрочненного слоя, давление в зоне деформации, а также влияют на прочность и износостойкость деформирующего инструмента. Большое влияние на усталостную прочность деталей оказывают остаточные напряжения в поверхностных слоях. При действии сжимающих остаточных напряжений в поверхностных слоях значительно возрастает усталостная прочность.

Многими исследованиями установлено [28–30], что именно потеря работоспособности поверхностного слоя, которая приводит к его дальнейшему разрушению, происходит в большинстве случаев в вершине упругопластической волны. Для оценки напряженного состояния в упругопластической волне использовали интенсивность напряжений по Мизесу [31–33], которая учитывает все главные компоненты тензора напряжений в точке тела и позволяет оценить прочность материала поверхностного слоя. Интенсивность временных напряжений во внеконтактной зоне деформации ( а вр ) определяется как:

авр = ^1.[(°вР — афр)2 + Кр — авр)2 + (авр — °в Р)2], где σвzр , σrвр , σвφр – главные компоненты временных напряжений, действующие по осям Oz, Or, Oφ.

Чтобы не определять интенсивность напряжений для достаточной большей номенклатуры параметров реверсивного ППД, нужно знать параметры, при которых возникают наибольшие напряжения в вершине упругопластической волны. Выше представлены результаты расчетов по влиянию параметров процесса реверсивного ППД на геометрические размеры упруго- пластической волны. Было сделано предположение, что интенсивность напряжений в упругопластической волне связана с ее геометрическими размерами. На рис. 11 представлена такая зависимость для упругопластической волны в направлении продольной подачи.

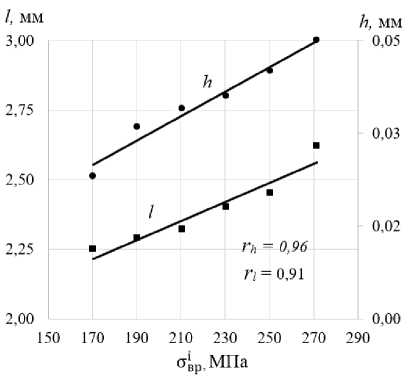
Рис. 11. Зависимость максимальной интенсивности временных напряжений в вершине волны от ее размеров в направлении продольной подачи

Fig. 11. Dependence of the maximum intensity of temporary stresses at the wave top on its dimensions in the direction of the longitudinal feed

Из рис. 11 видно, что в направлении продольной подачи с увеличением размеров упругопластической волны значения максимальной интенсивности временных напряжений в вершине волны возрастают.

а™, МПа

□ 60499 Max

533,29

— 471,6

— 404,9

— 333,2

■ 271,51

— 204,31

— 138,12

— 71,421

■■ 47253 Min

Osp МПа ■ 519.8 Max 462,07 — 404,33 — 346,6 — 288,36 J 231,13 — 173,39 — 115,66 ■ 57,92 1 0.18418 Min

а

b

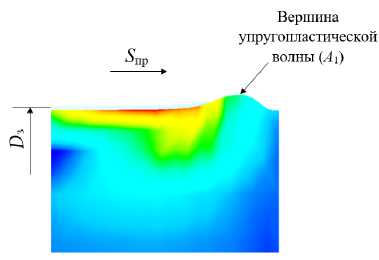
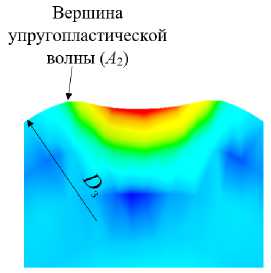
Рис. 12. Распределение интенсивности временных напряжений в упругопластической волне (при натяге t = 0,4 мм): а - в направлении продольной подачи ( А 1 ); b - в направлении главного движения ( А 2 )

Fig. 12. Distribution of intensity of temporary stresses in elasto-plastic wave (with preload t = 0,4 mm): a - in the direction of the longitudinal feed ( A 1 ); b - in the direction of the main movement ( A 2 )

Расчеты коэффициента корреляции показали достаточно высокую прямую зависимость σ ⁱ _вр от размеров упругопластической волны. Коэффициент корреляции, устанавливающей связь максимальной интенсивности напряжений с высотой упругопластической волны, составил 0,96, а с ее длиной - 0,91. Интенсивность временных напряжений в вершине волны достигает максимального значения при l = 2,62 мм и h = 0,045 мм (при t = 0,4 мм). Для этих размеров упругопластической волны были определены поля интенсивности напряжений, представленные на рис. 12.

На рис. 12 показано распределение интенсивности временных напряжений в упругопластических волнах в направлении продольной подачи ( а ) и в направлении главного движения ( b ). Установлено, что при натяге t = 0,4 мм в упругопластической волне ( А 1 ) интенсивность временных напряжений почти на 26 % выше по сравнению с напряжениями в упругопластической волне ( А ₂ ). В вершинах упругопластических волн создается интенсивность временных напряжений величиной 202-271 МПа, которые меньше в 2,4-3,2 раза предела прочности материала, что не являются причиной нарушения прочности обработанных поверхностей.

Заключение

• 1.    Линейные размеры упругопластических волн достигают максимума только при определенных значениях величины натяга (в данной работе t = 0,4 мм). При одинаковых условиях упрочнения размеры упругопластической волны в направлении продольной подачи больше, чем размеры упругопластической волны в направлении главного движения (получено следующие соотношения 1 1 = (1,2...1,4) 1 ₂ ; h 1 = (1,6...1,8) h ₂ ) . Изменение размеров упругопластической волны в направлении продольной подачи в основном вызывают технологические параметры, характеризующие кинематику рабочего инструмента (реверсивная частота вращения РИ, начальный угол установки РИ, амплитуда угла реверсивного вращения РИ, частота вращения заготовки, продольная подача). Эти параметры оказывают незначительное влияние на размеры упругопластических волн в направлении главного движения.

• 2.    Установлена зависимость геометрической формы упругопластической волны от физико-механических свойств материала. Большие размеры упругопластических волн при упругопластической деформации формируются у материала с пониженным пределом текучести и модулем упругости. Полученные результаты модели-

• рования позволяют описать соотношение высоты упругопластических волн от физико-механических свойств металлов в направлении продольной подачи: h1 = = (0,74…0,76).10-3 E; h1 = (0,22…0,25).10-3 σT.

• 3.    При большой величине натяга ( t = 0,4 мм) в вершинах упругопластических волн создается интенсивность временных напряжений величиной 202–271 МПа,