Внешняя устойчивость резонанса и стабилизация вращения космического аппарата с малой инерциальной и аэродинамической асимметриями при спуске в атмосфере Венеры

Проблема устойчивости резонансов при возмущенном движении относительно центра масс возвращаемых космических аппаратов в атмосфере рассматривалась в значительном количестве публикаций [1], [2], и в других работах. Внешняя устойчивость резонанса приводит к эволюции медленных переменных на нерезонансных участках движения, прилегающих к рассматриваемому резонансу. В работе [3], было сформулировано определение и получены условия внешней устойчивости резонанса в нелинейной системе с медленными и быстрыми переменными. Явление внешней устойчивости резонансов было обнаружено также в задаче о возмущенном орбитальном движении твердого тела с сильным магнитом в геомагнитном поле [4]. Применительно к задаче о спуске в атмосфере космического аппарата с малой асимметрией явление внешней устойчивости резонансов ранее рассматривалось в следующих работах [5], [6].

ПОСТАНОВКА ЗАДАЧИ

Ставиться задача по исследованию внешней устойчивости главного резонанса при спуске в атмосфере с малой аэродинамической и инерционной асимметриями космического аппарата. Космический аппарат (КА) рассматривается как твердое тело массой 10 кг и имеет форму, близкую к конической. При исследовании внешней устойчивости требуется рассмотреть только главный резонанс. Предполагается произвести анализ внешней устойчивости главного резонанса в квазилинейном случае (при малых значениях

угла атаки) с учетом изменения параметров движения центра масс. Квазилинейная постановка задачи позволит произвести подробный приближенно-аналитический анализ условия внешней устойчивости и определить возможные случаи устойчивости главного резонанса, которые подтверждаются численными результатами. Рассмотрим движение спускаемого КА с малыми значениями угла атаки в случае положительных ω x при выполнении условия ω _x - ω _1,2 <0.Следует отметить, что случаи отрицательных угловых скоростей и случаи положительных ω x при выполнении условия ω _x - ω _{1 2} >0 могут быть рассмотрены аналогичным образом.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ

Взаимное положение связанной с аппаратом системы координат OXYZ и орбитальной системы координат OXкYкZк определяется посредством трех углов ориентации: пространственного угла атаки α п, аэродинамического угла крена ϕ п и скоростного угла крена γa. В дальнейшем нижние индексы в данных углах ориентации не указываются. В качестве исходной рассматривается приближенная квазилинейная система уравнений движения КА с малой аэродинамической и инерционной асимметрией относительно центра масс в атмосфере, полученная в работе статье [7]. Данные приближенные квазилинейные уравнения получены из системы исходных нелинейных уравнений движения КА с малой асимметрией относительно центра масс методом асимптотического расщепления решений с учетом предположения о малости значений пространственного угла атаки [7], [2]. Указанные квазилинейные уравнения (1)-(2) учитывают, что в данной системе уравнений возможен главный резонанс, реализующийся при выполнении равенства: ωxr - ω1 ≅ 0 . Из решения этого урав- нения можно определить резонансное значение угловой скорости ωxr = ω/ 1 - Ix .

Квазилинейная система уравнений [7] рассматривается совместно с уравнениями, описывающими движение центра масс КА. Для космического аппарата, близкого по форме к осесимметричной, данные уравнения имеют вид [1]: dV/dt = - С_xvqS / m - g sin ϑ ,   (1)

вого сечения и длина аппарата; I _x = I _x /I ; I_x и I_y = I_z = I – моменты инерции аппарата относительно осей системы координат OXYZ, m _zn– коэффициент восстанавливающего аэродинамического момента . Здесь безразмерный параметр асимметрии равен m^A = m^A/ ω ² .

d ϑ / dt = C_yvSq / mV - g cos ϑ / V , (2)

ВНЕШНЯЯ УСТОЙЧИВОСТЬ РЕЗОНАНСА И СТАБИЛИЗАЦИЯ ВРАЩЕНИЯ АППАРАТА

dH/dt = Vsin ϑ .

В уравнениях (1)-(3) С_xv, C _yv – известные аэродинамические коэффициенты, ϑ – местный угол наклона траектории, m – масса аппарата, V – воздушная скорость КА, R – радиус Земли, H – высота полёта КА.

Квазилинейные уравнения содержат в правых своих частях быструю фазу θ , что существенно затрудняет применение данных уравнений для анализа внешней устойчивости главного резонанса. Усредняя квазилинейное уравнение для угловой скорости с учетом двух первых приближений в нерезонансном случае, получаем:

d ^{ω x} = ε A ^{( ω x )} + ε ² A ^{( ω x )} + ε ³ A ^{( ω x )} . (4) dt 1 2 3

Здесь первое и второе приближения метода усреднения, соответственно равны:

Для исследования внешней устойчивости главного резонанса Δ = ω _x - ω ₁ ≅ 0 требуется рассмотреть изменение на нерезонансных участках функции Ляпунова следующего вида 2

V = Δ [3]. Предположим, что КА имеет следующее сочетание моментов инерции I_x = 2I . В этом случае функция Ляпунова принимает вид: 22

V = ω _x + ω . При анализе внешней устойчивости применяется выражение для усредненной производной функции Ляпунова:

dV      dω

= 2ωx    x + 2ω   .(8)

dt          dtdt dω   ω dq

Здесь = ε . Далее верхние индексы dt 2q dt

A ₃( ω x ) ₌ ε

A 1( ω x ) ₌ 0,

A ( ₂ ω x ) ₌ 0, ₃ ( - 6 + 2 a ₁ ² _,2 + 3 a ₂ ² _,1 )( m^A ) ² m ^Δ ω ⁴ ω ₁ ² _,2

в выражениях ω x не указываются. Производная рассчитывается согласно выражению (4).Согласно теореме [3] одним из условий внешней устойчивости резонанса Δ = ω _x - ω ₁ ≅ 0 является

64( ω _x - ω _1,2 ) ² I x ω _a ²

cos(2 θ ₁ - 2 θ ₃ ) . (7)

условие:

dV

Здесь б - малый параметр, характеризующий малость параметров массовой и аэродинамической асимметрии и медленность изменения ω ; a_1,2 – амплитуды угла атаки, ∆= ω _x - ω ₁ – резонансно е соотно шение частот;

< 0 .

dt

При выполнении условия (9) величина

Δ эво-

люционирует к резонансной зоне ∆ ≅ o( ε ) . Напротив, выполнение условия (10) обеспечивает

I x ω

ω ₁ = 2 ^x + ω _a ; ω _a

Ixω x + ω2 ; mA , mΔ , θ , 41

«уход» величина Δ от резонансной зоны.

θ ₃ – функции, характеризующие величину и взаимное расположение аэродинамической и инер-

dV dt

> 0 .

A ционной асимметрий; m

m ₁ ^A

ω Φ       2 A

= -     m_{y 0} - I_xz ω _x , m ₂

mzп sinθ1 = m1A /mA ; cosθ1

⁼ ( m ₁ ^A )² + ( m ₂ ^A )²

ω Φ 2

=- m + I ω z xy x m_zп

= - m ₂ ^A / m ^A ;

,

;

m ^Δ

=   ( I yz )² + ( Δ I )² , sin 2 θ ₃ =Δ I / m ^Δ ,

cos 2 θ ₃ = - I yz / m ^∆ , ω =

- m ^α _zпqsl / I ,

ФФ my0 , mz0 – коэффициенты малых аэродинамических моментов от асимметрии формы КА; q – скоростной напор; S и L – площадь миделе-

В этом случае следует говорить о внешне неустойчивом резонансе Δ = ω _x - ω ₁ ≅ 0 .

Произведем анализ условия внешней устойчивости (9) при движении спускаемого КА с малыми значениями угла атаки в случае положительных ω x при выполнении условия ω _x - ω _{1 2} >0. Область реализации условия (9), следует оценивать следующим образом: ε <  Δ < 1/ ε . Нижняя граница указанной области по величине Δ соответствует границе резонансной зоны, которая имеет порядок ε . На верхней границе данной области по величине Δ порядок малости производной d ω _x / dt увеличивается на один

порядок ε , что в соответствии с уравнением (4) приводит к стабилизации усредненных величин ωx . Из условия (9) следует, что внешняя устойчивость главного резонанса Δ = ωx - ω1 ≅ 0 наблюдается при одновременном выполнении условий dωx / dt < 0 , ( dωx / dt < 0, ωx >0, ω >0. На рис. 1 и рис. 2 представлены результаты численного интегрирования квазилинейной величиной аэродинамической или инерционной асимметриями в представленной задаче может обеспечить выполнение заданных ограничений по углу атаки и угловой скорости КА. Однако подробное исследование управляемого движения КА выходят за рамки представленной статьи, но оно может быть рассмотрено в дальнейших публикациях.

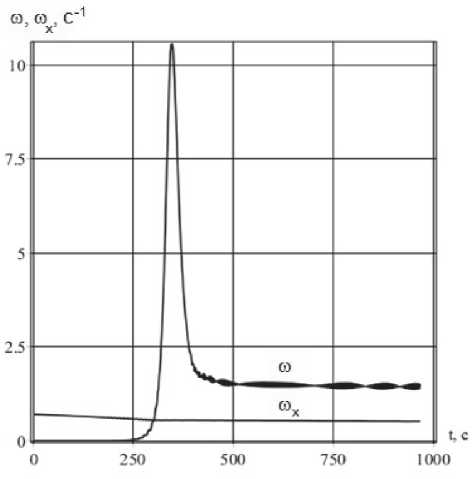
Рис. 1. Эволюция угловых скоростей ω _x (t) и ω (t) при внешне устойчивом резонансе

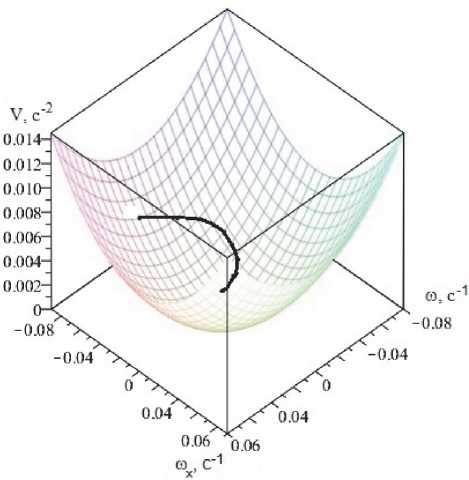
Рис. 2. Эволюция переменных V, ω _x (t) и ω (t) при внешне устойчивом резонансе

системы при реализации внешней устойчивости резонанса. Действительно, при нерезонансном уменьшении положительного значения угловой скорости ω x на участке уменьшения величины ω (t) осуществляется выполнение условий d ω _x / dt <  0, d ω / dt <  0 , ω x >0, ω >0. Такое поведение рассматриваемой системы соответствует внешней устойчивости резонанса Δ ≅ 0 . Кроме того, в этом случае наблюдается стабилизация вращательного движения КА. На рис. 2 изображено изменение переменных ω _x и ω в трехмерном пространстве в рассматриваемом случае внешней устойчивости главного резонанса.

ВЫВОДЫ

Таким образом, применение метода усреднения и условия внешней устойчивости главного резонанса при малых величинах угла атаки позволяют обеспечить стабилизацию вращения асимметричного космического аппарата в атмосфере Венеры, имеющего следующее сочетание моментов инерции I_x = 2I . Следует отметить, что практический интерес представляет изучение вопросов, связанных с выбором величин параметров асимметрии КА. В этой связи, применение закона управления