Внутренние усилия и перемещения стелечного узла обуви под воздействием нагрузки

Витебский государственный технологический университет

ЭЛЕМЕНТ БАЛКИ, УПРУГАЯ СВЯЗЬ, ПЕРЕМЕЩЕНИЯ, ВНУТРЕННИЕ УСИЛИЯ, ВЕКТОР-СТОЛБЕЦ, ТРАНСПОНИРОВАНИЕ, МАТРИЦА ЖЁСТКОСТИ

В статье рассматривается алгоритм определения деформированного состояния балки, моделирующей стелечный узел обуви, позволяющий найти внутренние усилия (поперечные силы и изгибающие моменты), а также упругие перемещения (прогибы и углы поворота поперечных сечений) под действием сосредоточенных сил в условиях кусочно-линейной жёсткости поперечных сечений упругих связей (трапеций в плане).

Поставленная задача решается исходя из принципа виртуальных перемещений. На базе алгебры матриц связываются векторы-столбцы заданных сосредоточенных сил и моментов с внутренними усилиями.

Последние выражаются посредством матрицы жёсткости через деформации, а деформации – через перемещения. Как результат получаем уравнения равновесия в перемещениях.

Матрицы жёсткости строятся путём интегрирования приближенных дифференциальных уравнений упругих связей с переменной по длине жёсткостью (изменяющейся по линейному закону).

Результаты работы могут использоваться при анализе деформированного состояния низа обуви. При этом может решаться как прямая задача определения перемещений при заданных силовых факторах, так и обратная (возможно, более важная) подбора жёсткостей поперечных сечений стелечного узла, обеспечивающих заданные перемещения.

ELEMENT OF THE BEAM, ELASTIC JOINT, MOVEMENT, INTERNAL EFFORTS, VECTOR-COLUMN, TRANSPOSE, STIFFNESS MATRIX

The article describes the development of algorithms that always allow dealing with deformed states of systems. These systems include assembled shoe insoles. As a model, the author used an elastic beam loaded with concentrated forces (and, possibly, concentrated moments). The relatively smooth outlines of the assembled insoles are replaced by a broken outline. Infinitely small load-bearing elements are represented by assembled insoles connected by trapezoidal elastic bonds. Integration of approximate differential equations of plane bends resulted in the final construction of mathematical equations.

Algebra made it possible to compactly formulate the equilibrium equations connecting the rear force factors. Recent changes in the matrix reflect the relationship between internal forces and deformations.

However, the task of displacements finding is simplified.

As a result, a matrix algorithm was found that allows not only to find the stress-strain state of the node trunk, but also to solve the problem of selecting its sections that provide the required displacements.

The article describes an example of determining the deflections and rotation angles of a pinched assembled insole. The calculation results are comparable with experimental data.

Известно, что в обуви с каблуком для обеспечения надёжной опоры своду стопы, обеспечения правильного положения стопы в процессе ходьбы, геленочная часть обуви (особенно с увеличением высоты каблука) должна обладать определенной жесткостью и оказывать сопротивление оказываемым нагрузкам.

Для обеспечения объективной оценки качества стелечных узлов обуви, а также для прогнозирования величины прогибов геленочной части стелечного узла при эксплуатации, необходима разработка методики расчёта, позволяющей найти внутренние усилия (поперечные силы и изгибающие моменты), а также упругие перемещения стелечного узла обуви под воздействием нагрузки.

Авторами [1] была разработана расчётная схема несущей конструкции женской обуви, в которой геленочная часть обуви была представлена балкой. Нагрузки, действующие на геленочную часть обуви, заменили более простой и удобной для расчёта схемой. Разработанная ме- тодика была проверена на экспериментальном образце, анализ результатов показал, что теоретическая модель низа женской обуви позволяет с точностью только до 15 % оценивать прогибы геленочной части низа обуви.

Таким образом, целью данной работы являлась разработка алгоритма определения деформированного состояния стелечного узла обуви, который позволит с достаточной степенью точности определять прогибы (перемещения) стелечного узла обуви под воздействием нагрузки, что даст возможность осуществить рациональный подбор материалов для стелечного узла ещё на этапе конструкторско-технологической подготовки производства обуви.

При разработке методики расчёта внутренних усилий и перемещений стелечного узла для низа обуви необходимо составить и обосновать расчетную схему нагружения. Стелечный узел в обуви представим балкой с кусочно-линейной жёсткостью, нагруженной сосредоточенными силами и моментами (рисунок 1).

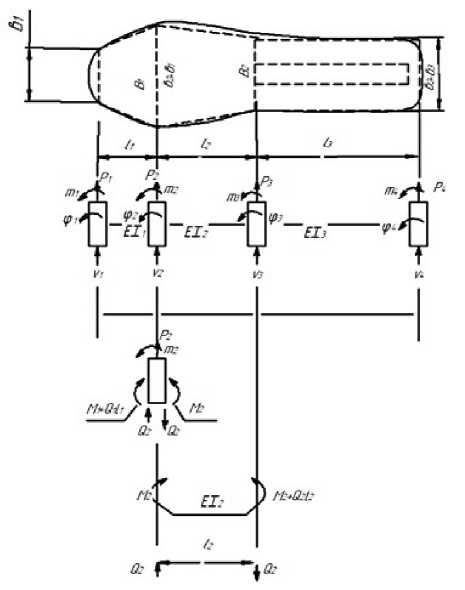
Рисунок 1

– Несущие элементы с упругими связями

Следуя принципу виртуальных перемещений [2, с. 448], напишем уравнение

,        (1)

Ы         /=1

или

Р-^-^(Др) = О

откуда следуют уравнения равновесия

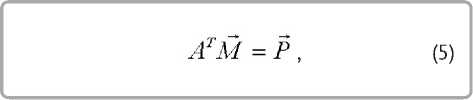
и уравнение равновесия в перемещениях

,           (6)

В уравнении (1) введены матричные векторы-столбцы (2) заданных сил; внутренних сил; перемещений бесконечно коротких элементов, выделенных из балки; деформаций упругих связей между ними.

—

R1	га ~		Avj
mY	MY		А^
Рг	Qi	1,2	Af2
Р = т2 ,М =	мг	v= Фг ,Av =	(2)
Р„	Qm	Vn	A^ra
тп	м„	фп	А^

Деформации связаны с перемещениями:

где использовался закон Гука с матрицей жёсткости С

М = CAv

Матрицы А (3) и А^т (5) взаимно транспонированы.

Заметим: матрицу А^т в уравнениях равновесия элементов балки (5) можно получить, составляя их обычным образом как уравнения проекций и моментов (рисунок 1); соответственно получаются выражения для деформаций (3), то есть, в конечном счёте, уравнения для перемещений

.                     (7)

,                       (3)

их вариации

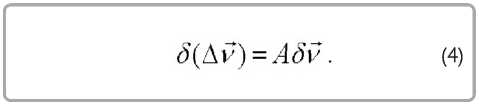
Для примера рассмотрим балку с тремя элементами на рисунке 1. Уравнения равновесия её трех элементов (5)

Используя вариации (4) в уравнении (2) и транспонируя его, получим

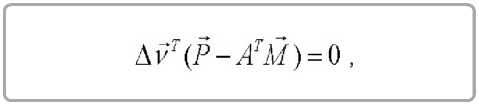
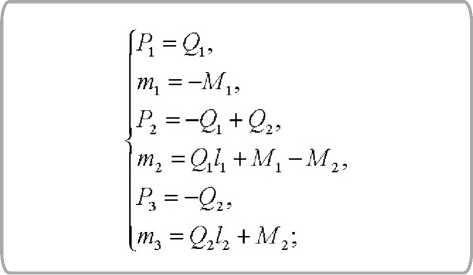
их матрица

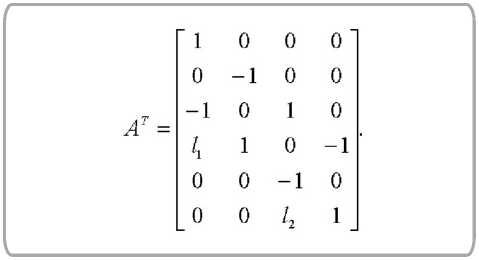
Деформации (3)

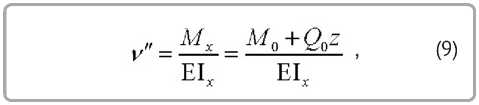
где жёсткость текущего поперечного сечения

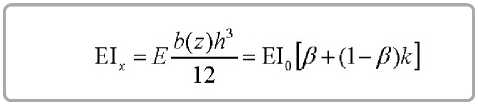
и введены обозначения

Лг =

о о о

о

-1

о о

-1

О

О

1 о -1

О о -1 о

о о

Ф1

^2

A i'i = 1'! — v₂ + v М\ = (-ф1+Фз),

А^з =(-9^,2⁺9’з)-

л

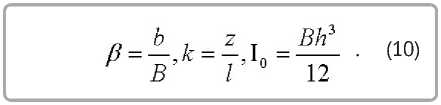
Дифференциальное уравнение (9) принимает в обозначениях (10) вид

Фз.

X.

Найдём теперь матрицу жесткости в законе (7).

Проинтегрируем дифференциальное уравнение упругой кривой трапециевидной упругой связи (рисунок 2)

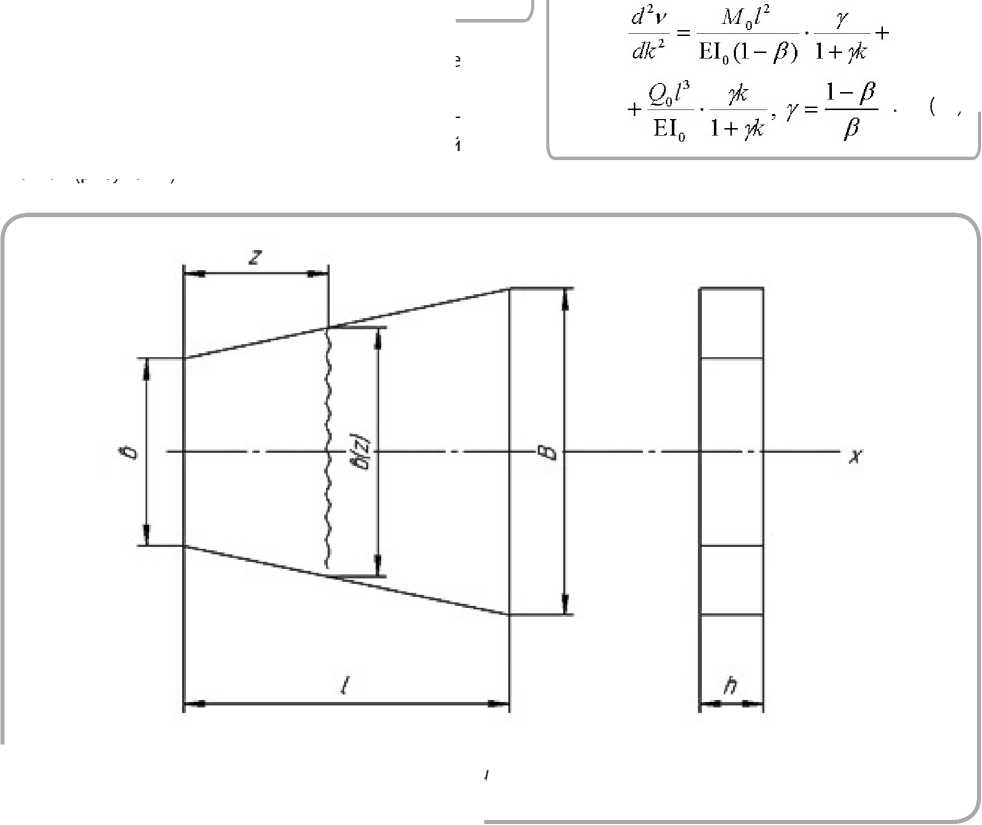
Рисунок 2 – Упругая связь соседних элементов балки

После интегрирования уравнения (11)

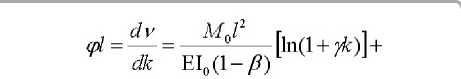
Как видим, матрица уравнений (14) симметричная. В упомянутом выше предельном переходе при β → 1, γ → 0

, QJ³

+ EIO(1-/?)

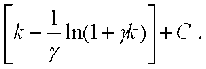
-                         "                 (15)

EI, Am = 1 Q/3+A+,/2.

Постоянную интегрирования в формуле (12) найдём из начального условия φ ( z = 0) = = φl ( k = 0) = φ₀l : C = φ₀l .

После второго интегрирования с подстановкой начального условия v ( z = 0) = v₀ получим выражение

Из уравнений вида (14, 15) внутренние усилия выражаются через деформации (8), образуя матрицу жёсткости, в «овалах» которой заключены нули.

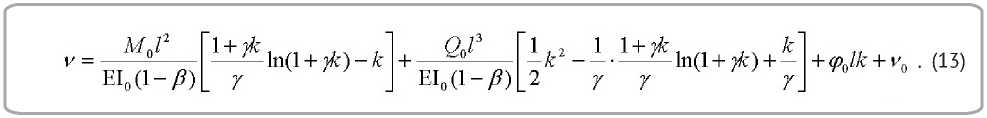
Заметим: в случае балки с кусочно-постоянной жёсткостью формулы (12, 13) получают вид (в результате предельного перехода по Лопита-лю при β → 1, γ → 0), известный как решение, полученное методом начальных параметров [3, с. 337].

Располагая формулами (12, 13), найдём вначале выражения для деформаций (8) (полагая в указанных формулах k = 1). Выразим угол поворота и перемещение, например, элемента 2 (рисунок 1):

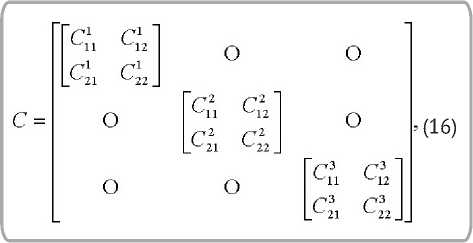
EIO1(1-Д)г2 = Е101(1-№ + Е101(1-/?М +^i

1 + у           1         1 + у

—АЧп(1 + /) + — +M^ —-ln(l + /)-l r r] L Y " .

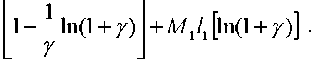
Е101(1-А)<р2=Е101(1-А)?>1+ф12

После этого деформации (8)

Eui-ijA^az31+4

2 у

}L\n(\-P^k=QJ3

in(i+/)-! +M.P i-lin(i+/) ,

Y

l-lln(l + y) +MJI [ln(l + /)] .

Последняя из симметричных матриц 2×2 (её элементы помечены верхним индексом 3) имеет вид, следующий из уравнений (15):

На рисунке 3 изображена расчётная схема стелечного узла, представленная балкой с кусочно-линейной (изменяющейся вдоль балки по линейному закону) жёсткостью поперечного сечения.

Для проверки расчётных значений на практике было проведено экспериментальное исследование прогибов стелечного узла на устройстве для испытания геленков, стелечных узлов и готовой обуви на жесткость и упругость, разработанном с профессором Горбачиком В.Е. [4, 5]. Устройство позволяет максимально приближать условия нагружения при испытании к реальным нагружениям геленочной части при эксплуатации.

Для исследования использовался стелечный узел наиболее распространённой в настоящее время конструкции: полустелька нижняя (картон повышенной жёсткости MERCKENS CJM 888 2,5 мм ) + основная стелька (картон Flexan 1,5 мм ) + геленок (сталь) + полустелька верхняя (картон MERCKENS CJM 158 1,2 мм ).

При проведении исследования стелечный узел неподвижно закреплялся в пяточной части (точка 4 на рисунке 3), нагрузка прикладывалась в точке 1 (носочная часть узла), величина прогибов измерялась в точках 1, 2, 3. На рисунке указаны расчётные значения прогибов, а в скобках – значения, полученные экспериментальным путём. Как видно, для точек 1, 2, 3 расхождения расчётного и экспериментального значений для данного стелечного узла составили 8,3 %, 8,7 % и 5,6 % соответственно (расхождения могут быть вызваны неоднородностью свойств материалов).

Таким образом, расчётные значения и величины прогибов, полученных экспериментальным путём, различаются в пределах 10 %. Перемещения геленочной части стелечного узла, которые нас интересуют, отличаются от расчёт-

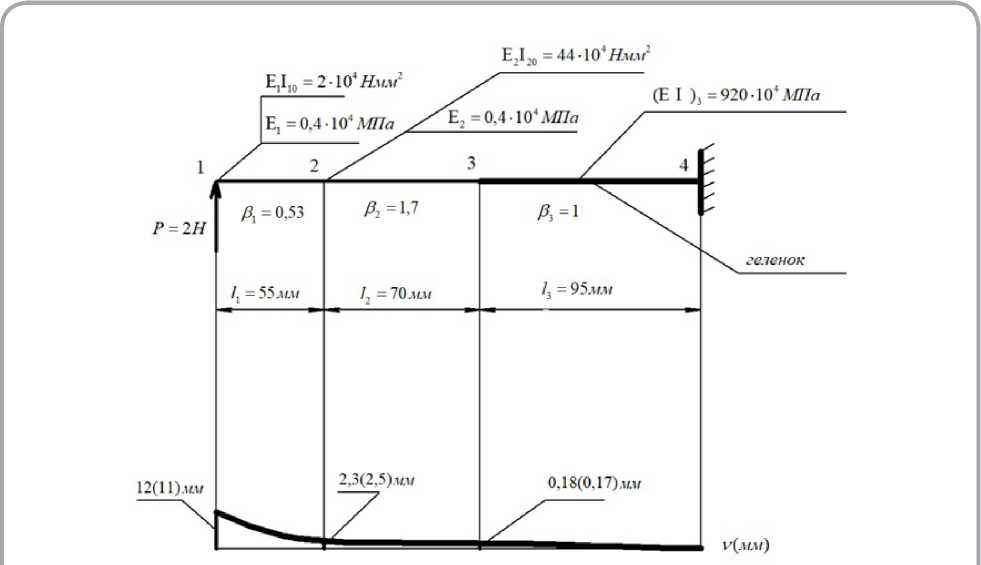
Рисунок 3 – Прогибы балки-модели (рисунок 1)

ных значений только на 8,7 %, следовательно, разработанный алгоритм позволяет достаточно точно определять прогибы стелечного узла под воздействием нагрузки, что даёт возможность оценивать жёсткость стелечного узла, не проводя дополнительных исследований.

Внутренние усилия М в уравнении (7) выражаются посредством двух матриц – матрицы жёсткости (16) и транспонированной матрицы уравнений равновесия (5), входящей в уравнение (8), через перемещение (2). Для трёх участков заделки имеем

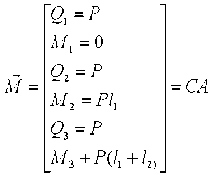
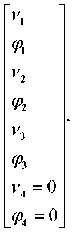
где структура матрицы жёсткости С представлена выражением (16), транспонированная матрица уравнений равновесия, аналогичная матрице

(8),

Выражения (19) получаются перемножением матриц 2×2 в матрице (16) на матрицы (2×4) в матрице (18). В защемлённом узле перемещения v ₄ , φ₄ равны нулю. Два последних уравнения (17,19) дают перемещения v ₃ , φ₃ . Их подстановка во вторую группу уравнений (17,19) даёт опять же систему двух уравнений, откуда находятся перемещения v ₂ , φ₂ . Наконец, их подстановка в первые два уравнения даст систему двух уравнений относительно v ₁ , φ₁ . Именно так находятся перемещения на рисунке 3.

Таким образом, полученный алгоритм может быть распространён на любое число участков, с любым числом сил с произвольными очертаниями упругих связей и легко поддаётся программированию. Алгоритм с достаточной степенью точности позволяет определить прогибы стелечного узла при заданной нагрузке при использовании различных конструкций и различных материалов комплектующих, поэтому может быть использован для рационального подбора материалов, обеспечивающих жёсткость геленочной части стелечного узла на этапе конструкторско-технологической подготовки производства, что позволит выпускать обувь с заданным уровнем потребительских свойств.

1—
	10-1^ 3 0 0 0
	0-10 1 _Э 0 00
	0 0   1   0 -1 L 0 0
	(18)
	0 0   0    0    1    0 -1 /3
	0 0   0   0   0 -1 0 1

В произведении в правой части уравнения (17) получим линейные алгебраические выражения, образующие вектор-столбец

	ГАу^ф^ф.)
	51(Ч,^,1'2,^2)
	Гг^Фг^Ф^
	йАУг.ФгЗ'^фА ’	(19)
	ГзАЧ^ФзАл,Ф^
	МУ^ФЗ'У^Ф4Х

В статье приняты следующие обозначения: P(H) - вектор-столбец, P^T - векторы-строки заданных сил Р(Н) и моментов m . ( Н^мм ); M - вектор-столбец внутренних сил - поперечных сил Q i (Н) , изгибающих моментов М . ( Н^мм ), перемещений несущих элементов (рисунок 1) - прогибов v_t ( мм ), углов поворота ф . ( рад ), деформаций упругих связей Av i ( мм ), Аф . ( рад ); А , А^т - матрица и транспонированная матрица: первая матрица линейной связи деформаций и перемещений, вторая – матрица уравнений равновесия, С - матрица жёсткости; М_о ( Н^мм ), Q_o ( Н ) - начальные изгибающий момент, поперечная сила; 1₀ ( мм⁴ ) - момент инерции начального поперечного сечения, ф⁰ ( рад ), v₀ ( мм ) - угол поворота и прогиб начального сечения.