Волновая динамика ширины годичных слоев дуба

Автор: Мазуркин Петр Матвеевич, Тишин Денис Владимирович

Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc

Статья в выпуске: 5 т.16, 2014 года.

Бесплатный доступ

Для анализа ширины годичных слоев были взяты керны из стволов семи дубов ( Quercus robur L.) на пробной площади около г. Зеленодольск Республики Татарстан. По дереву № 5 с 1774 по 2004 гг. даны математические модели ежегодной динамики ширины годичных слоев. Модель содержит более 100 асимметричных вейвлет-сигналов. Для них можно провести эвристическую идентификацию причин появления каждого колебательного возмущения дуба по радиальному приросту в ходе его развития и роста. Дана матрица параметров модели, сравнены дубы по биологическому времени и показаны графики закономерностей. Приведены результаты прогноза ширины годичного слоя дерева № 5 до 2050 г.

Еще

Дуб, ширина годичных слоев, радиальный прирост, динамика, вейвлеты, сравнение

Короткий адрес: https://sciup.org/148203298

IDR: 148203298

Текст научной статьи Волновая динамика ширины годичных слоев дуба

Для изучения строения и свойств растущих деревьев без их разрушения применяют метод керна [2, 4, 5]. Керны древесины, извлекаемые из растущих деревьев при помощи возрастных и приростных буравов Пресслера, сохраняют все свойства дерева [1], что позволяет получить необходимые данные при исследованиях возрастной структуры, прироста по диаметру, структуры и плотности древесины отдельных деревьев и древостоев.

В практикуме [2] и статьях [12-16] изложены способы измерения ширины годичного слоя с точностью до 1 мкм, а также ширины поздней и ранней древесины, с использованием технологии ГИС.

Статистическим моделированием [10, 17, 22] выявляют волновые закономерности динамики радиального роста ствола дерева, а по полученной статистической модели прогнозируют изменение радиуса ствола дерева в перспективу и ретроспективу [2].

Опыт моделирования в дендрохронологии показан в [3, 7-9, 18]. Получены закономерности ширины годичного слоя поэтапного [16] для сосны 250 лет и минимаксного градиентного анализа ряда в 650 лет [11] ставропольской ели на керне древесины.

По данным [6] минимаксным градиентным анализом получены волновые формулы для ширины годичных слоев можжевельника возраста 808 лет.

Цель статьи – показать новый метод вейвлет-анализа [10, 22] ширины годичного слоя дуба че-решчатого. При этом предполагается, что измере-

ния и датировка годичных колец до моделирования выполнены [19].

РАЙОН И ОБЪЕКТ ИССЛЕДОВАНИЯ

Дендрохронологический материал отбирался в лесу Зеленодольского лесничества, кв. 115. Координаты пробной площади широта: 55º51'25''N, долгота: 48º29'05''E. Почва дерново-подзолистая. Тип леса - липняк осоково-снытевый с дубом и елью. В подлеске средней густоты преобладают лещина обыкновенная, бересклет бородавчатый и подрост липы. В травостое доминируют сныть обыкновенная и осока волосистая. Максимальный возраст дубов достигает 250 лет.

Например, дерево № 5 имеет следующие показатели: высота ствола – 24 м , диаметр на уровне груди – 77 см. Начало замера первого годичного слоя на керне древесины равно t 0 для 1790 г. (табл. 1). Текущий биологический возраст дуба равен t + 16 лет, то есть дуб начал расти с 1774 г. Возраст при взятии керна на высоте 1,3 м в 2004 г. составил A 2004 1774 230 лет.

МЕТОДИКА ИЗМЕРЕНИЙ

Отбор кернов древесины проводился в 2005 г. возрастным буром Suunto на высоте 1,3 м по одному случайному радиусу с семи дубов. В лабораторных условиях образцы были подготовлены к измерениям по общепринятой методике [20]. Ширина годичных колец измерялась с помощью полуавтоматического измерительного комплекса LINTAB с точностью до 0,01 мм.

По данным измерений строились графики абсолютного радиального прироста, которые использовались для точной датировки годичных слоев методом перекрестной датировки [21]. Качество датировки оценивалось с помощью программы TSAPWin [23]. Перекрестная датировка – это сравнение сходных графиков изменения ширины годичных слоев у разных деревьев и выбор точного места на кернах, где соответствие между ширинами максимально.

Метод перекрестной датировки позволяет проводить относительную и абсолютную датировку времени формирования радиального прироста древесины у ствола по ширине годичных слоев.

Относительная датировка позволяет определить возраст анализируемых образцов относи- тельно друг друга, для которых календарная дата не определена.

Абсолютная датировка определяет календарную дату годичных слоев на керне. Она выполняется в том случае, если известна календарная дата взятия образца древесины хотя бы у одного дерева [19].

Таблица 1 . Данные измерений ширины годичных слоев дуба № 5 и привязка к шкале времени

Год	Время t , лет	b , 10² мм	Год	Время t , лет	b , 10² мм	Год	Время t , лет	b , 10² мм	Год	Время t , лет	b , 10² мм	Год	Время t , лет	b , 10² мм
1790	0	110	1833	43	162	1876	86	80	1919	129	189	1962	172	186
1791	1	108	1834	44	149	1877	87	74	1920	130	264	1963	173	144
1792	2	141	1835	45	105	1878	88	83	1921	131	202	1964	174	130
1793	3	164	1836	46	132	1879	89	120	1922	132	126	1965	175	133
1794	4	149	1837	47	142	1880	90	137	1923	133	124	1966	176	79
1795	5	142	1838	48	184	1881	91	53	1924	134	84	1967	177	126
1796	6	84	1839	49	121	1882	92	101	1925	135	98	1968	178	125
1797	7	79	1840	50	124	1883	93	64	1926	136	101	1969	179	103
1798	8	68	1841	51	100	1884	94	110	1927	137	159	1970	180	156
1799	9	64	1842	52	102	1885	95	84	1928	138	79	1971	181	151
1800	10	110	1843	53	143	1886	96	66	1929	139	161	1972	182	160
1801	11	64	1844	54	198	1887	97	82	1930	140	149	1973	183	153
1802	12	90	1845	55	140	1888	98	64	1931	141	156	1974	184	157
1803	13	123	1846	56	151	1889	99	69	1932	142	136	1975	185	118
1804	14	96	1847	57	126	1890	100	119	1933	143	112	1976	186	164
1805	15	143	1848	58	74	1891	101	110	1934	144	76	1977	187	115
1806	16	89	1849	59	93	1892	102	135	1935	145	122	1978	188	107
1807	17	101	1850	60	126	1893	103	218	1936	146	104	1979	189	70
1808	18	84	1851	61	101	1894	104	284	1937	147	106	1980	190	88
1809	19	126	1852	62	84	1895	105	261	1938	148	149	1981	191	90
1810	20	94	1853	63	99	1896	106	222	1939	149	134	1982	192	99
1811	21	99	1854	64	70	1897	107	181	1940	150	127	1983	193	142
1812	22	84	1855	65	103	1898	108	148	1941	151	150	1984	194	134
1813	23	72	1856	66	79	1899	109	110	1942	152	98	1985	195	103
1814	24	121	1857	67	74	1900	110	213	1943	153	112	1986	196	84
1815	25	109	1858	68	123	1901	111	220	1944	154	96	1987	197	91
1816	26	74	1859	69	98	1902	112	211	1945	155	111	1988	198	90
1817	27	79	1860	70	80	1903	113	128	1946	156	126	1989	199	106
1818	28	78	1861	71	69	1904	114	126	1947	157	121	1990	200	113
1819	29	76	1862	72	71	1905	115	309	1948	158	139	1991	201	110
1820	30	121	1863	73	73	1906	116	297	1949	159	141	1992	202	92
1821	31	143	1864	74	84	1907	117	220	1950	160	198	1993	203	70
1822	32	64	1865	75	80	1908	118	194	1951	161	179	1994	204	56
1823	33	53	1866	76	52	1909	119	259	1952	162	191	1995	205	74
1824	34	110	1867	77	81	1910	120	153	1953	163	213	1996	206	71
1825	35	205	1868	78	132	1911	121	218	1954	164	183	1997	207	66
1826	36	201	1869	79	130	1912	122	163	1955	165	180	1998	208	64
1827	37	189	1870	80	106	1913	123	254	1956	166	186	1999	209	72
1828	38	164	1871	81	116	1914	124	126	1957	167	167	2000	210	86
1829	39	181	1872	82	54	1915	125	164	1958	168	199	2001	211	75
1830	40	191	1873	83	96	1916	126	155	1959	169	190	2002	212	66
1831	41	164	1874	84	61	1917	127	184	1960	170	174	2003	213	72
1832	42	142	1875	85	59	1918	128	170	1961	171	143	2004	214	81

ЛИНЕЙНАЯ МОДЕЛЬ

В дендрохронологии принята линейно-агрегированная модель [19], отражающая формирование ширины годичного кольца: bA+C+D+D+E , (1)

где: A – тенденция роста, вызванная естественным процессом старения, C – воздействие климатических факторов, D - эндогенные воздействия, на- пример, плодоношение, D - экзогенные воздействия, например, воздействия вредителей, загрязнения и т. д., E - случайная составляющая.

Формула (1) показывает, что общий сигнал в каждый год t может быть разделён на влияние ряда естественных и антропогенных факторов, воздействующих на произрастающее дерево. Однако в реальности динамика ширины годичного слоя явно не линейна, так как нелинейно изменчивы все факторы.

Факторы могут влиять на радиальный прирост как положительно, так и отрицательно. И это обстоятельство не позволяет выявлять адекватные закономерности, так как положительные и отрицательные влияния математически уничтожают друг друга. Из формулы (1) становится ясна основная задача экологических исследований – выделить «след», оставленный интересующим нас фактором.

Однако моделирование ширины годичных колец, как правило, проводится с помощью сплайн-функций. Недостатками являются неизвестность стыков между сплайн-функциями и допущение об одинаковых средних арифметических и равных дисперсиях у этих средних.

Фактически дисперсия всегда переменна, то есть ряд измеренных значений ширины годичных слоев скедастичен. Поэтому линейный метод дает только грубые ориентировочные оценки. При этом невозможна обратная эвристическая идентификация процессов, повлиявших на ход развития и роста дерева.

Поэтому получается, что у каждого динамического ряда в значительной степени исключены индивидуальные особенности радиального роста ствола дерева и сохранена в линейном методе только общая для данного дерева изменчивость (сигнал).

Мы предлагаем совершенно новый подход.

РЯД РАДИАЛЬНОГО ПРИРОСТА СТВОЛА

ДЕРЕВА КАК ЧЕРЕДА АСИММЕТРИЧНЫХ ВЕЙВЛЕТ-СИГНАЛОВ

Физико-математический подход [2, 7, 10, 22] предполагает понимание динамического ряда ширины годичных слоев как отражения какого-то сложного и составного процесса развития и роста ствола дерева.

Сигнал - это материальный носитель информации. А информация нами понимается как мера взаимодействия. Сигнал может генерироваться, но его приём не обязателен [10, 22]. Так, например, ежегодный ряд годичных слоев людям известен умозрительно несколько сот тысяч лет, но суть его как множества сигналов до сих пор не раскрыта.

Сигналом может быть любой физический процесс, но его свойства по ряду годичных слоев пока непонятны. Получается, что изменение множества неизвестных сигналов давно известно. И ремесленники это знали давно и понимали интуитивно, например, при изготовлении музыкальных инструментов (например, скрипки Страдивари).

Поэтому примем ряд ширины годичных слоев за фрактальное множество аналоговых сигналов , изменяющихся непрерывно в шкале календарного времени. Для удобства календарную шкалу заменим шкалой времени измерений t .

Тогда любой асимметричный сигнал можем записать как гармоничный вейвлет [10, 20] вида b Acos( t / p a ) ,

A a t^a ² exp( a t^a ⁴ ) , p a a t^a ⁷ , (2)

где A - амплитуда (половина) вейвлета (ось y ), p - полупериод колебания (ось x ), a ...a - парамет ры модели (2), значения которых по данным измерений выявляются в программной среде CurveExpert-1.40.

По формуле (2) с двумя фундаментальными постоянными e и (иррациональные числа), образуется квантованный изнутри изучаемого явления или процесса вейвлет-сигнал. Причем квантование происходит по фрактальным уровням.

Понятие вейвлет-сигнала позволяет абстрагироваться от неизвестного явления или процесса. Мы уверены в том, что выявленные закономерности как суммы вейвлетов – будет важным событием. Как и в живой клетке: сигнал – это событие, имеющее регуляторное значение для функционирования клетки.

Есть аналогия с сигналами в ряду радиального прироста из-за живых клеток, которые вначале нужно выявить как асимметричные вейвлеты (табл. 2).

Таблица 2. Параметры общего уравнения динамики годичного радиального прироста дуба № 5

Но мер i	Вейвлет b _i a ₁ _i t^a ² ⁱ exp( a ₃ _i t^a ⁴ ⁱ )cos( t /( a ₅ _i a ₆ _i t^a ⁷ ⁱ ) a ₈ _i )								Коэфф. коррел. r
	амплитуда (половина) колебания				полупериод колебания			сдвиг
	^a 1 i	^a 2 i	^a 3 i	^a 4 i	^a 5 i	^a 6 i	^a 7 i	^a 8 i
1	124,35486	0	0,0086631	0,74861	0	0	0	0	0,7431
2	6,18065e-33	23,68868	1,72906	0,62818	0	0	0	0
3	1,47924	1,04672	0,013393	1	37,44509	0,48830	0,44264	4,32027
4	79764,925	8,39401	19,40156	0,19160	20,45747	0	0	-0,56569
5	8,13082e-35	81,19211	0,15114	1,02129	0,97826	0	0	5,95901	0,1780
6	-2,95406e-62	36,55117	0,062279	1,28958	1,85804	0	0	3,16216	0,2514
7	12,76947	0,29541	0,10908	0,49229	2,50339	0,0020570	1,22195	-4,67285	0,3703
8	-6,27729	0,54576	0,30712	0,37334	11,33170	-0,00036758	1,48945	-4,69337	0,3127
9	1,88998	10,52780	16,03522	0,23276	3,84305	0	0	0,91353	0,1728
10	8,27902e-31	18,29686	0,028758	1,30792	3,27262	-0,0048695	0,51592	1,03351	0,2998
11	-0,18961	1,37240	0,023034	1	8,03973	0	0	-0,74639	0,2281
12	8,07674e-45	28,51831	0,26412	1,00092	3,03788	-0,0010004	1,13801	-2,85011	0,3173

Но мер i	Вейвлет b a ₁ _i t^a ² ⁱ exp( a ₃ _i t^a ⁴ ⁱ ) cos( лt /( a ₅ _i + a ₆ _i t^a ⁷ ⁱ ) a ₈ _i )								Коэфф. коррел. r
	амплитуда (половина) колебания				полупериод колебания			сдвиг
	^a 1 i	^a 2 i	^a 3 i	^a 4 i	^a 5 i	^a 6 i	^a 7 i	^a 8 i
13	-1,77190e-28	18,56339	0,16713	1,01388	7,60500	-0,0021550	1,22325	-3,68494	0,5566
14	5,52100e-27	28,03478	2,54973	0,74307	4,78171	-0,040599	0,99638	-4,81651	0,2893
15	31,39545	0	0,025848	1	5,90079	-0,090622	0,95158	1,80007	0,3375
16	-7,56653	0	0,0060341	1	9,13846	0	0	3,22654	0,1752
17	-7,59675	0	0	0	15,51592	-0,00027403	1,56536	0,66782	0,2971
18	-8,74266	0	0,00049328	1	1,47150	0	0	5,18104	0,3397
19	-7,92880	0	0,0079695	1	-91,10629	96,75157	0,019987	5,06625	0,1831
20	2,73887e-36	19,59899	0,10002	1	3,02573	-5,08663e-8	1	-0,29248	0,1572
21	-5,84292e-28	11,86111	0,069867	1	3,49321	-9,20822e-8	1	1,40070	0,1667
22	-2,24931e-21	18,92424	0,48166	1	3,64434	-0,034254	1	-2,72486	0,2581
23	1,03887e-54	33,16320	0,25579	1,01188	1,66542	0	0	5,53530	0,1411
24	1,14528e-63	40,01659	0,36718	1	2,08569	3,39894e-8	1	-2,43999	0,2898
25	1,23518e-25	17,82508	0,67108	0,75767	1,11750	0	0	-5,02227	0,4068
26	8,37736	0	0,010167	1	1,31614	0	0	-0,98724	0,2181
27	-0,51511	0	-0,013457	1	1,50531	0	0	-1,74556	0,2139
28	-12,20143	0	0,0087604	1	4,27140	0	0	-0,82516	0,3538
29	1,13151	0	-0,0062645	1	4,03058	0,00024158	1	4,63667	0,1555
30	-0,23567	0	-0,016215	1	2,07132	0	0	1,16720	0,1796
31	1,96790e-51	31,70000	0,27381	1	1,06594	2,28616e-7	1	-1,06999	0,2273
32	-5,01483e-6	8,75497	0,58186	0,97825	1,57541	-0,016473	1,04492	-5,31113	0,3366
33	-1,29069e-5	4,43167	2,89311	0,23643	14,35272	-0,088260	0,80230	-6,19949	0,2833
34	-1,65820e-6	5,92462	1,40986	0,47871	1,46748	0	0	5,03203	0,1605
35	1,86085e-34	26,49267	0,45636	1,01481	19,08224	-0,099408	1,04481	-5,74662	0,1371
36	-1,18217e-19	11,38164	0,076226	1,00788	15,61352	-0,012663	0,90261	1,66740	0,2046
37	5,64078e-55	40,81476	0,66015	1	0,54146	0,0079956	1,00643	0,62188	0,2853
38	-0,0081334	1,56469	0,015754	1	1,29452	3,00752e-6	1	-0,0063180	0,1369
39	2,96598e-31	18,34277	0,12889	1	1,17118	1,14449e-8	1	-3,16000	0,4140
40	5,58301e-98	69,11868	0,96261	1	1,30365	-3,09359e-6	1	5,74476	0,2427
41	-1,51768e-21	12,18647	0,021096	1,25155	1,25346	0	0	2,71572	0,3710
42	4,35763e-7	3,74453	0,038709	0,87377	2,23025	0	0	-1,03892	0,2034
43	-1,21507e-72	36,76029	0,0070526	1,56212	1,08127	0	0	3,35812	0,2557
44	2,11873e-45	40,46730	1,09576	1,00246	1,07211	0,00023247	1,21307	0,55760	0,2359
45	0,67192	0	-0,0033550	1	34,96421	-7,46024	0,11113	-1,84214	0,1032
46	183,30873	6,49112	10,30113	0,26465	3,29588	0	0	-3,21999	0,3215
47	13,84184	0	0,12281	1	1,46441	0	0	-0,99679	0,2243
48	-1,71475	0	-0,0030693	1	7,05622	-0,028188	0,9943	0,25647	0,2585
49	-2,42842e-84	65,16534	1,21839	0,99932	1,82088	-0,0059698	0,98516	-5,38814	0,1664
50	2,19290e-18	10,64723	0,076415	0,99955	4,14387	-0,0049282	1,00633	-3,52404	0,2519
51	-2,59478e-36	20,46266	0,11367	1,01858	1,35127	0	0	1,05872	0,4490
52	1,82999e-37	22,34597	0,033452	1,35247	1,32427	0	0	4,45279	0,2066
53	7,55751e-14	8,27483	0,075095	1	1,09532	4,21687e-7	1	-0,088773	0,1207
54	-2,21050e-6	4,92258	0,57963	0,58216	1,55736	0	0	2,94400	0,3219
55	-9,09211e-14	8,16295	0,16287	0,82705	1,21581	0	0	-3,52174	0,1797
56	-1,39182	0	0,0060135	1	3,44883	0,024519	0,53424	1,43657	0,1266
57	-5,47328e-8	4,05269	0,0013233	1,51500	15,30715	-0,20920	0,63309	-1,99494	0,2693
58	-2,49361e-57	40,89073	0,61879	0,98921	0,98051	0	0	5,53344	0,2810
59	-7,21572	2,25150	1,06565	0,80305	1,13396	0	0	-1,48847	0,1882
60	-7,63845e-26	28,09234	1,54531	0,93505	0,65395	0,0080204	1,00937	-0,042402	0,1182
61	0,92639	0,22763	0,0044581	1	1,80362	0	0	-1,35500	0,2687
62	-0,044969	0,72157	0	0	1,61187	0	0	-2,55446	0,2438
63	-1,84828e-13	17,52475	7,85362	0,40563	1,71113	0,16915	0,15185	-0,57125	0,2613
64	1,09268e-34	21,95574	0,17490	1,09051	1,87494	0	0	-5,73041	0,1825
65	-4,62383e-13	6,24829	0,010214	1,11922	1,97061	0	0	5,16052	0,2189
66	3,86943e-35	17,70810	0,072041	1	2,81002	0,0024589	1,40611	0,61598	0,0934
67	-2,69657e-100	50,77866	0,059632	1,22299	1,78920	0	0	0,71710	0,1853
68	-0,087259	0	-0,0089403	1	10,98965	-0,0016368	1	0,24213	0,0523
69	-4,00125	0	0,0056211	1	2,37861	0	0	-0,76955	0,4955
70	0,25205	0	-0,012708	1	1,42013	0	0	-4,25833	0,3820
71	-1,58488	0	0,018787	1	160,68481	-2,14810	0,99973	-0,24447	0,1626
72	-0,21694	0	-0,00068106	1	24,83494	-0,00031560	1,75372	-2,27120	0,0589
73	-0,059287	0	-0,018155	1	0,97104	0	0	-4,47386	0,2445
74	-0,22758	0	-0,0068125	1	1,13498	0	0	1,74628	0,1471

Но мер i	Вейвлет b a ₁ _i t^a ² ⁱ exp( a ₃ _i t^a ⁴ ⁱ ) cos(Я t /( a ₅ _i + a ₆ _i t^a ⁷ ⁱ ) a ₈ _i )								Коэфф. коррел. r
	амплитуда (половина) колебания				полупериод колебания			сдвиг
	^a 1 i	^a 2 i	^a 3 i	^a 4 i	^a 5 i	^a 6 i	^a 7 i	^a 8 i
75	4,13888	2,65307	0,050260	0,90246	52,54827	-0,72031	0,61120	1,25680	0,0622
76	4,05864	0	0,013226	1	2,67555	0	0	0,14118	0,4596
77	-0,98299	0	0,0097769	1	6,53795	-5,76705e-5	1,28070	0,54411	0,1444
78	0,79432	0,10062	0	0	2,31921	6,15415e-6	1	-6,14807	0,3764
79	1,22028	0,19717	0	0	0,99991	0	0	1,60759	0,0164
80	-0,93637	0,34700	0	0	1,37257	6,42858e-7	1	-0,11143	0,1515
81	0,00066962	1,49870	0	0	3,06228	0	0	-3,95759	0,3478
82	-7,63813e-20	9,67693	0,0078435	1,27142	2,54503	0	0	-2,45830	0,3249
83	-2,10924e-29	16,59752	0,11641	1	1,48789	-6,38128e-7	1	1,09344	0,1474
84	-6,43330e-6	4,13335	0,51283	0,57092	3,27188	0,0013804	1,05055	5,22402	0,2683
85	-1,38294e-71	46,46095	0,70765	0,92443	2,91431	-0,0016938	0,78783	-0,27316	0,3226
86	-0,60477	0,10276	0	0	1,90285	0,010277	0,90958	1,00676	0,3963
87	-1,62156e-14	8,20124	0,088515	0,95907	14,94702	-0,00094433	1,37725	0,66309	0,0757
88	2,48381e-12	7,34602	0,065631	1	3,75357	0,15491	0,23022	-3,77147	0,4776
89	1,36688e-76	45,55015	0,35875	1	1,75228	3,74092e-7	1	6,00875	0,3075
90	-3,66288e-7	7,47877	0,34259	1	1,14660	0,43907	0,11309	0,50329	0,2979
91	7,81674e-5	2,69087	0,00093597	1,90843	2,31205	0	0	-1,46156	0,1314
92	1,93620e-30	16,98333	0,11874	1	2,34243	-1,31912e-5	1	0,97264	0,0974
93	-3,25128e-12	9,36199	0,20967	0,99864	1,48166	-0,00016004	1,16574	-0,22127	0,1628
94	1,22243e-88	39,98288	0,052087	0,99995	0,85676	0	0	3,47658	0,1848
95	-5,04760e5	22,13341	49,94094	0,18224	1,64363	0	0	-4,82610	0,2811
96	-8,97864e-28	15,80114	0,28510	0,82270	1,33387	0	0	3,56744	0,1924
97	-5,76831e-54	29,23315	0,11212	1,07049	0,94700	0	0	3,21891	0,3690
98	9,23585e-40	20,97871	0,10968	1	1,42082	4,93588e-8	1	3,01175	0,1794
99	3,60159e-58	33,43511	0,26667	0,97469	1,17635	0	0	1,83692	0,3305
100	5,02427e-19	11,06550	0,090349	0,99616	4,62990	-0,0027739	1,11923	-0,68996	0,5026
101	4,41306e-72	38,59475	0,20359	1	0,59091	-1,35929e-9	1	1,88000	0,2433
102	3,47800e-17	9,90446	0,35273	0,71249	1,89910	0	0	0,41727	0,2660
103	2,77052e-50	27,76253	0,16494	1,00904	3,78015	-0,00045276	0,85124	2,00775	0,1911
104	-3,55744e-65	36,43236	0,23323	1	1,57605	4,42517e-8	1	3,21817	0,1880
105	-1,69099e-13	20,15343	8,87675	0,44015	1,22966	0	0	4,91828	0,2965
106	-0,35388	0	-0,00041049	1	-10,80777	14,78410	0,017394	4,88175	0,3636
107	-2,54618	0	2,25359	1	0	0	0	0	0,2585

ТРЕНД И ДВЕ ВОЛНЫ

Всего было получено 107 составляющих, из которых первые два члена составляют тренд (рис. 1).

S = 44.78422513 r = 0.48470952

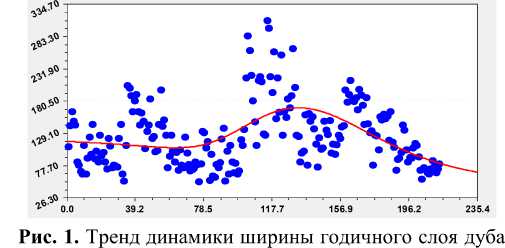
№ 5

Затем последовательно появляются два колебания (рис. 2) с переменными амплитудой и периодом.

Эти четыре составляющие образуют формулу, с параметрами из таблицы 2 и общим коэффициентом корреляции 0,7431 > 0,7 (сильная связь), вида bb+b+b+ b4 , (3)

b 124,35486exp( 0,0086631t 0,74851) , b 6,18065 10 33 t 23,68868 exp( 1,72906t0,62818), b A cos(71t/p 4,32027),

A 1,47924t1,04672 exp( 0,013393t) , p 37,44509 0,48830t0,44264 , b A cos(71t/p2 +0,56569),

A 79764,925t8,39401 exp( 19,40156t0,19160) , p 20,45747 .

Первый член формулы (3) по закону экспоненциальной гибели всегда показывает естественную тенденцию, а второй и последующие члены статистической модели характеризуют природные или антропогенные (внешние и внутренние) влияния.

Вторая составляющая показывает стрессовое возбуждение организма дуба как генетический отклик на изменение фенотипических условий произрастания. Если бы мы знали историю развития и роста дуба за 220 лет, то вполне могли бы провести обратную эвристическую идентификацию событий.

Программная среда по своим возможностям помещает всего четыре составляющие (рис. 3).

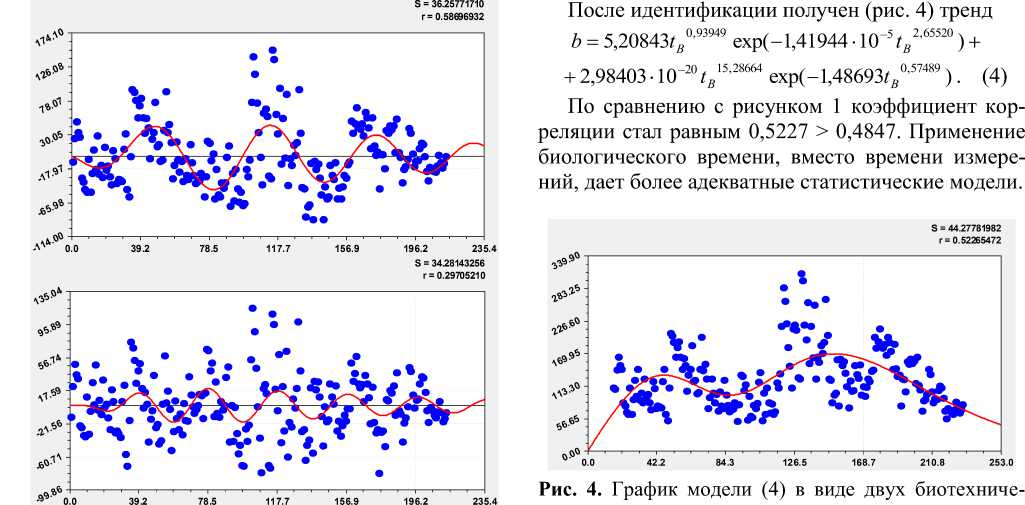
ских законов

Рис. 2. Две волны колебательного возмущения

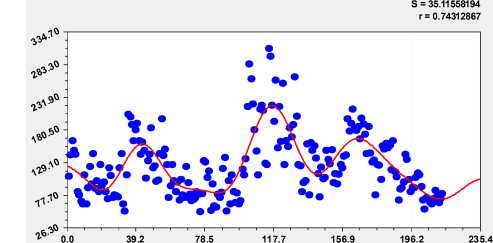
Рис. 3. График модели (3) с четырьмя членами

АНАЛИЗ ПАРАМЕТРОВ МОДЕЛИ

Интерес представляет изменение амплитуды колебания 2 a в 1790 г.

Вейвлет № 71 имеет максимальный начальный период 2 X 160,68481 321,4 года. А минимальный период 1,08 года наблюдается у вейвлета № 37.

При этом все волновые члены общей формулы делятся на две группы:

а) конечномерные вейвлеты 3-14, 20-25, 31-44, 46, 49-55, 57-67, 75, 78-105 (у них a 2 i ^ 0 );
б) бесконечномерные вейвлеты 15-19, 26-30, 45, 47, 48, 56, 68-74, 76, 77, 106 (у них a 2 i 0).

Особое место занимает член № 107, показы вающий необходимость учета биологического времени.

ВЛИЯНИЕ БИОЛОГИЧЕСКОГО ВРЕМЕНИ

Оно равно t_B t + 16 лет, когда жёлудь дуба №5 пророс в 1774 г. Очевидно, что в первый год у проростка ширина годичного слоя равна нулю.

При таком допущении получается, что тренд должен состоять из двух биотехнических законов [10, 20]. Добавим в табл. 1 строку при условии t 16 ширину b 0 и изменим шкалу t t +16.

ДРУГИЕ ДУБЫ

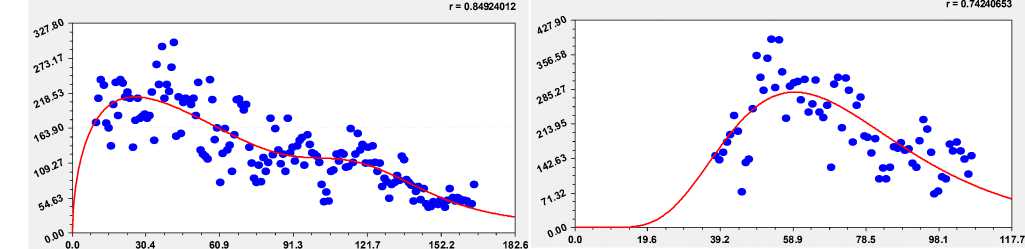
Проверим общий закон [10, 20] на других шести дубах (табл. 3 и рис. 5).

Дубы имеют следующее время в начале замера последнего от периферии ствола годичного слоя: № 1 – 9 лет; № 2 – 11; № 3 – 10; № 4 – 38; № 5 – 16; № 6 – 15; № 7 – 34 года .

Полный по биологическому времени керн дает лучшие результаты и по моделированию.

Например, дуб № 4 дал только одну составляющую от общей формулы тренда b a t a2 exp( a3tB 4 ) +

+ a t ^a ⁶ exp( a ₇ t_B^a ⁸ ).

Наибольшую адекватность получил дуб № 3, а наименьшую по коэффициенту корреляции – № 6.

ФРАКТАЛЬНЫЕ ГРУППЫ ВЕЙВЛЕТОВ

Всего были идентифицированы 106 вейвлетов (107-е уравнение вспомогательное из-за непринятия шкалы биологического времени) по семи группам составляющих общей модели.

Группировка вейвлетов выполнена по скачкам снижения максимальных остатков по модулю к max , как это показано в табл. 4.

Нулевой номер члена общей модели соответствует среднему арифметическому значению b .

Цена деления прибора равна 0,01 мм или 10 мкм. Тогда погрешность измерения будет равна ±5 мкм. Группы вейвлетов выделены по шкале остатков (абсолютной погрешности моделирования): 1) более 200 X 5 = 1000 мкм; 2) от 1000 до 500 мкм; 3) 500 – 250 мкм; 4) 250 – 125 мкм; 5) 125 – 60 мкм; 6) 60 – 40 мкм; 7) менее 40 мкм (табл. 4).

S = 34.4430 r = 0.7744

S = 34.30007572 r = 0.78937490

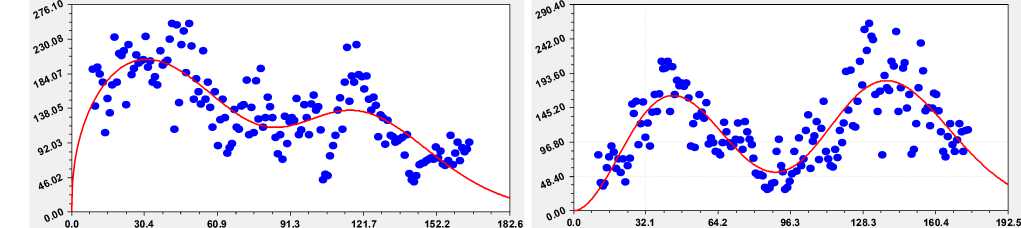
б№1

дуб №2

S = 56.57961798

S = 33.493

б№4

б №3

S = 28.92074009 r = 0.81128185

S = 43.48

r = 0.37

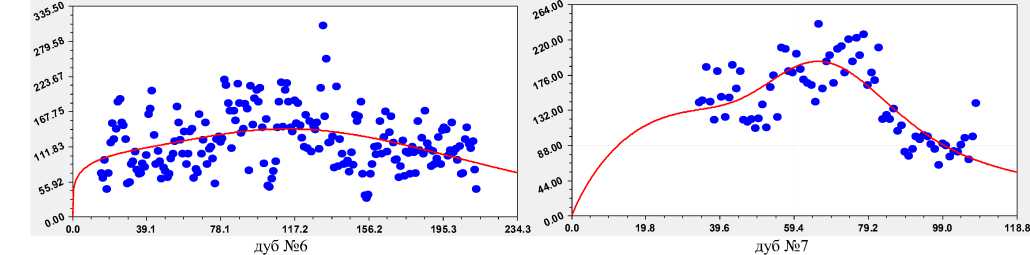
Рис. 5. Графики влияния биологического времени на тренд ширины годичного слоя у шести дубов

Таблица 3. Параметры тренда динамики ширины годичного слоя дубов от биологического времени

Номер дуба	Тренд b _B a t ^a ² exp( a ₃ t _B ⁴ ) + a ₅ t _B ^a ⁶ exp( a ₇ t _B ^a ⁸ )								Коэфф. коррел. r
	амплитуда (половина) колебания				полупериод колебания			сдвиг
	a ₁	a ₂	a ₃	a ₄	a ₅	a ₆	a ₇	a ₈
1	59,58902	0,41593	0,00017844	2,04635	3,28122e-32	20,30193	0,16373	0,99680	0,7744
2	0,34295	1,87453	0,00048048	2,00097	4,71973e-38	22,34916	0,059256	1,17072	0,7894
3	63,62527	0,53589	0,020718	1	1,96918e-53	32,97515	0,27359	1	0,8492
4	1,74949e8	28,43590	52,76943	0,21978	0	0	0	0	0,7424
5	52,08428	0,93949	1,41944e-5	2,65520	2,98403e-20	15,28664	1,48693	0,57489	0,5227
6	52,58525	0,21338	0,00020407	1,61246	9,15608e-7	4,49569	0,031274	1	0,3785
7	11,98383	0,91299	0,024203	1	1,58158e-28	21,19486	0,30877	1	0,8113

АНАЛИЗ ФРАКТАЛЬНОСТИ СУММЫ ВЕЙВЛЕТОВ

Разные по форме сигналы самоподобны, т.е. фрактальны через общую модель типа (2).

Известно, что фракталы подобны через закон Мандельброта y a exp( a x) . Для фрактальной модели суммы вейвлетов показателем стала максимальная абсолютная погрешность (остаток) кmax .

По данным табл. 4 получили (рис. 6) формулу max | = 1829,860 exp( 0,15483i0,70934) +

+A cos( 71i / p 0,66347) , (6)

A 58,40831i0,86288 exp( 0,11493i) , p 0,87957 + 0,017078i1,57394 .

S = 25.60336350 r = 0.99746189

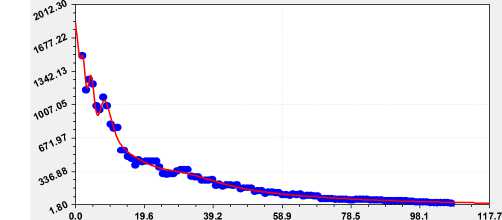
Рис. 6. График формулы (6) фрактального изменения остатков (абсолютной погрешности) от влияния номера составляющей

Таким образом, асимметричный вейвлет (2) позволяет с высокой адекватностью при коэффициенте корреляции 0,9975 показывает возможность количественного описания неизвестных в прошлом процессов поведения дуба № 5. Для эвристической идентификации прошлого поведения необходимы результаты феноменологических наблюдений.

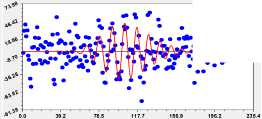
Графики вейвлетов с наибольшими значениями коэффициента корреляции даны на рис. 7.

Амплитудно-частотный анализ каждого вейвлета позволит определить причины поведения растения. При этом на дуб влияет множество процессов.

Таблица 4. Фрактальное снижение остатков (мкм) после составляющих модели (табл. 2)

1 группа		2 группа		3 группа				4 группа				5 группа		6 группа		7 группа
i	к max	i	к max	i	к max	i	к max	i	к max	i	к max	i	к max	i	к max	i	к max
0	1831	9	997	15	490	28	318	40	196	50	168	59	107	77	59	95	38
2	1501	10	813	16	470	29	341	41	209	51	135	60	107	78	53	96	35
3	1155	11	769	17	405	30	353	42	188	52	143	61	99	79	53	97	32
4	1259	12	776	18	455	31	353	43	203	53	143	62	108	80	58	98	32
5	1213	13	550	19	438	32	353	44	203	54	120	63	107	81	60	99	31
6	997	14	550	20	441	33	291	45	198	55	132	64	108	82	57	100	30
7	958			21	440	34	282	46	202	56	128	65	94	83	58	101	26
8	1082			22	440	35	282	47	165	57	125	66	98	84	53	102	26
				23	439	36	253	48	171	58	125	67	98	85	54	103	26
				24	379	37	253	49	171			68	94	86	53	104	26
				25	314	38	249					69	92	87	53	105	26
				26	311	39	254					70	64	88	47	106	25
				27	315							71	64	89	46	107	18
												72	66	90	46
												73	67	91	46
												74	59	92	43
												75	61	93	43
												76	61	94	43

S = 16.41 r = 0.33

S = 20.79913279 r = 0.55660582

вейвлет № 13

S = 18.64 r = 0.33

S = 11.71285242 r = 0.35383197

S = 13.1987 r = 0.4068

5^*6

вейвлет № 18

Вейвлет № 25

вейвлет № 28

v^.^ J ■1У

вейвлет № 15

S = 5.20 r = 0.44

S = 4.7 r = 0.3

1.^

39.2

78.5 117.7 156.9 196.2

S = 3.07 r = 0.49

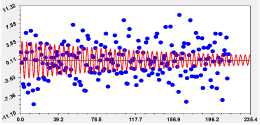
S = 2.83961157 r = 0.38202176

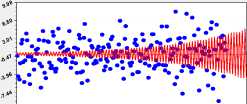
39.2 78.5 117.7 156.9 196.2 235.4

----------- ---------% --------е* е е

И ---------------|-------fl —1—1 1---------------■

0.0 39.2 78.5 117.7 156.9 196.2

вейвлет № 51 вейвлет № 54 вейвлет № 69 вейвлет № 70

Рис. 7. Графики вейвлетов (табл. 2) динамики ширины годичного слоя дуба № 5 с коэффициентом корреляции не менее 0,3

Из графиков на рис. 7 видно, что многие вейвлеты произошли в прошлом. Поэтому вейвлет-анализ дает возможность составить прогнозную математическую (статистическую) модель.

ПРОГНОЗИРОВАНИЕ ПОВЕДЕНИЯ ДУБА ПО ШИРИНЕ ГОДИЧНОГО СЛОЯ

Компьютер дал ту последовательность членов, которая поэтапно идентифицируется программной средой CurveExpert-1.40. Череда сигналов от разложения сложного динамического ряда ширины годичных слоев у дуба № 5 не совпадает с номером вейвлета. Но эту череду надо уточнять только после проведения процедуры упаковки всех 107 составляющих общей модели типа (2), а для этого нужен новый программный комплекс, позволяющий одновременно учитывать десятки вейвлетов с несколькими сотнями параметров модели.

Для составления прогнозной модели нужно отобрать те члены, которые с 2004 г. будут влиять на изменение ширины годичного слоя. Вполне очевидно, что появляются новые воздействия, поэтому прогнозирование возможно только условно. Причем с ростом горизонта прогноза вероятность появления расчетной ширины годичного слоя уменьшается (погрешность моделирования возрастает).

Дерево выдерживает взятие до 11-12 кернов [4] без изменения физиологических процессов. Поэтому для проверки прогнозных моделей необходимо в конце 2014 г. отобрать по одному керну с этих же деревьев.

Тогда горизонт прогноза определяем в 10 лет.

В табл. 5 даны результаты расчетов по прогнозной модели, в которой были оставлены следующие члены из табл. 2 с номерами: 1-4, 7-9, 11, 16-21, 2630, 33, 34, 36, 38, 39, 42, 43, 45, 48, 50, 51, 54-57, 61, 62, 65-70, 72-74, 78-82, 84, 86, 95-98, 102, 106. Для основания прогноза для 57 действующих членов взят интервал времени 1980-2004 гг. Отброшенные 50 членов статистической модели мало влияют после 1980 г. на динамику b .

Таблица 5. Основание прогноза дуба № 5

Год	Время t , лет	b , 10² мм	Расчетные значения
Год	Время t , лет	b , 10² мм	^bp	8	\, %
1	2	3	4	5	6
1980	190	88	86,3	1,7	1,93
1981	191	90	98,4	-8,4	-9,33
1982	192	99	104,3	-5,3	-5,35
1983	193	142	140,2	1,8	1,27
1984	194	134	129,6	4,4	3,28
1985	195	103	97,2	5,8	5,63
1986	196	84	79,1	4,9	5,83
1987	197	91	100,0	-9	-9,89
1988	198	90	88,4	1,6	1,78

Окончание таблицы 5

1	2	3	4	5	6
1989	199	106	117,1	-11,1	-10,47
1990	200	113	107,7	5,3	4,69
1991	201	110	109,3	0,7	0,64
1992	202	92	81,6	10,4	11,30
1993	203	70	68,6	1,4	2,00
1994	204	56	59,5	-3,5	-6,25

1995	205	74	80,5	-6,5	-8,78
1996	206	71	75,6	-4,6	-6,48
1997	207	66	68,1	-2,1	-3,18
1998	208	64	55,9	8,1	12,66
1999	209	72	66,9	5,1	7,08
2000	210	86	77,3	8,7	10,12
2001	211	75	82,4	-7,4	-9,87
2002	212	66	71,0	-5	-7,58
2003	213	72	79,7	-7,7	-10,69
2004	214	81	80,8	0,2	0,25

Без 50 членов с 1980 по 2004 гг. основание прогноза дает максимальную относительную погрешность 12,66%.

Статистическая модель по табл. 2 дает возможность прогноза на одну треть полного основания 230 / 3 до 2080 г.

В табл. 6 с учетом повышающейся погрешности моделирования дан прогноз до 2050 г.

Осенью 2014 г. появится практическая возможность проверки прогноза за 2005-2014 гг.

ЗАКЛЮЧЕНИЕ

Идентификация устойчивых закономерностей позволяет преобразовать табличные модели, которых много накопилось в дендрохронологии, например в [6], в высокоадекватные волновые уравнения с переменными амплитудами и периодами колебательного возмущения.

Эта текущая информация о взаимодействии растущего дерева со своей окружающей средой запоминается в годичных слоях древесинного тела дерева [7]. Тогда появляется задача дешифровки записанной информации в виде отдельных колебаний некоторой длины в хронологическом времени.

За свою жизнь в главном стебле дерева накапливается множество волн возмущения живых клеток при их одревеснении. При этом принимается допущение, что усушка керна древесины до проведения измерений вызывает пропорциональные изменения в размерах клеток и годичных слоев.

Применение предложенных методов и методик [7-18] к коротким рядам до 150-250 лет не представляет особых трудностей. Однако процесс идентификации весьма трудоемкий.

Таблица 6. Прогноз ширины годичного слоя дуба

Год	Время t , лет	b p , X 10² мм	Год	Время t , лет	b p , 10² мм	Год	Время t , лет	b p , 10² мм
2005	215	68,5	2021	231	83,1	2037	247	77,1
2006	216	52,5	2022	232	56,8	2038	248	107,4
2007	217	73,2	2023	233	77,2	2039	249	34,9
2008	218	95,8	2024	234	98,1	2040	250	52,3
2009	219	100,2	2025	235	123,6	2041	251	78,4
2010	220	79,2	2026	236	124,5	2042	252	55,4
2011	221	107,1	2027	237	97,5	2043	253	73,4
2012	222	106,3	2028	238	109,6	2044	254	123,0
2013	223	110,5	2029	239	151,0	2045	255	64,4
2014	224	76,5	2030	240	128,5	2046	256	84,2
2015	225	72,1	2031	241	105,9	2047	257	44,8
2016	226	74,9	2032	242	140,5	2048	258	17,0

2017	227	87,9	2033	243	79,5	2049	259	60,4
2018	228	54,0	2034	244	76,4	2050	260	100,5
2019	229	72,3	2035	245	91,0
2020	230	78,1	2036	246	63,4

Поэтому для автоматизации моделирования необходима разработка специализированной программной среды. Она может быть создана на базе наших методик эвристической, структурной и параметрической идентификации устойчивых законов распределения.

Дендроэкологический мониторинг прошлого у территории, на которой произрастает древостой, возможен по модельным и учетным деревьям, а также по отведенным лесоводами в рубку деревьям хозяйственного назначения. Вместе с тем дендро-экологический мониторинг и потребность в надежных экологических прогнозах, как было показано в данной статье, потребует перехода к учетным деревьям и применения в будущем неразрушающих и частично разрушающих (многократным взятием кернов из стволов и ветвей испытуемых деревьев) методов дендрохронологии.

Список литературы Волновая динамика ширины годичных слоев дуба

Бюсген М. Строение и жизнь наших лесных деревьев/Пер. с нем. М.-Л.: Гослесбумиздат, 1961. 424с.
Варсегова Л.Ю., Мазуркин П.М., Фадеев А.Н. Практикум по экологическому древоведению/под ред. проф. П.М. Мазуркина. Йошкар-Ола: МарГТУ, 2010. 42 с.
Верхунов П.М., Мазуркин П.М. Таксация древесного ствола лесных насаждений: Учеб. пос. Йошкар-Ола: МарГТУ, 1999. 72 с.
Колесникова А.А. Исследование свойств древесины по кернам. Йошкар-Ола: МарГТУ, 2002. 178 с.
Использование кернов древесины в лесоводственных исследованиях: Метод. рекомендации/Д.П. Столяров, О.И. Полубояринов, Н.Н. Декатов и др. Л.: ЛенНИИЛХ, 1988. 43 с.
Ловелиус Н.В. Изменчивость прироста деревьев. Дендроиндикация природных процессов и антропогенных воздействий. Л.: Наука, 1979. 232 с.
Мазуркин П.М. Дендрометрия. Статистическое древоведение: учеб/пос. Часть 1. Йошкар-Ола: МарГТУ, 2003. 308 с.
Мазуркин П.М. Дендрохронологические шкалы разновозрастного сосняка//Современные наукоемкие технологии. № 6. 2010. С. 32-44.
Мазуркин П.М. Дендрохронологические шкалы и возрастная структура разновозрастного сосняка. 12 с. Портал WOOD.RU. URL: http://www.wood.ru/ru/loa732.html.
Мазуркин П.М. Решение 23-ой проблемы Гильберта//Междисциплинарные исследования в области математического моделирования и информатики. Матер. 3-й научно-прак. internet-конф. Ульяновск: SIMJET, 2014. С 269-277.
Мазуркин П.М. Статистическое моделирование многоцикловых процессов//Циклы природы и общества: материалы VI Международной конференции. Часть 1. Ставрополь: Изд-во Ставр. ун-та, 1998. С. 213-218.
Мазуркин П.М., Варсегова Л.Ю. Испытание растущего дерева//Успехи современного естествознания. № 4. 2010. С. 38-43.
Мазуркин П.М., Варсегова Л.Ю. Измерение ширины годичного слоя на керне древесины//Успехи современного естествознания. № 4. 2010. С. 31-38.
Мазуркин П.М., Варсегова Л.Ю. Измерение ширины годичных слоев сердцевины и присердцевинной зоны растущего дерева с использованием кернов//Деревообр. пром-сть. 2010. № 2. С. 25-26.
Мазуркин П.М., Варсегова Л.Ю. Ультразвуковое испытание древесины растущего дерева на радиальных кернах//Деревообр. пром-сть. 2010. № 3. С. 29-30.
Мазуркин П.М., Демаков Ю.П. Особенности многоволновой динамики радиального прироста сосны//Циклы природы и общества: материалы VI Международной конференции. Часть 2. Ставрополь: Изд-во Ставр. ун-та, 1998. С. 174-176.
Мазуркин П.М., Филонов А.С. Математическое моделирование. Идентификация однофакторных статистических закономерностей: учебное пособие. Йошкар-Ола: МарГТУ, 2006. 292 с.
Мазуркин П.М., Филонова Е.С. Метод анализа дендрометрических данных//Экология: Образование, наука, промышленность и здоровье: материалы II Международной научно-практической конференции. Вестник БГТУ. 2004. № 8. Часть V. С. 83-85.
Тишин Д.В. Дендроэкология (методика древесно-кольцевого анализа): учебно-метод. пос. Казань: Казанский университет, 2011. 33 с.
Шиятов С.Г. и др. Методы дендрохронологии. Часть I. Основы дендрохронологии. Сбор и получение древесно-кольцевой информации: Учебно-методическое пособие. Красноярск: КрасГУ, 2000. 80 с.
Douglass A.E. Climatic cycles and tree-growth. A study of the annual rings of trees in relation to climate and solar activity. -Washington: Carnegie Inst., 1919. Vol. 1. 127 p.
Mazurkin P.M. «Wavelet Analysis of a Number of Prime Numbers». American Journal of Numerical Analysis, vol. 2, no. 2 (2014): 29-34 DOI: 10.12691/ajna-2-2-1
Rinn F. TSAP-Win -time series analysis and presentation: dendrochronology and related applications. Heidelberg, Germany. 2003. 91 p.

Еще

Статья научная