Волновая теория слоистых пластин с приближенным учетом поперечного сдвига

Динамические задачи, описывающие распространение волн в ограниченных средах, моделирующих элементы конструкций машин и аппаратов, отвечают запросам практики. Возникновение этой постановки связано с появлением большого количества прикладных задач, в которых необходима проверка прочности конструкции при кратковременных внешних воздействиях.

Первой отечественной работой в этой области является, по-видимому, монография [3], в которой сформулирован и решен широкий круг задач по определению воздействия импульсных нагрузок на элементы конструкций.

В решении задач о поведении тел при импульсном нагружении выделяется метод, основанный на использовании общих энергетических соотношений, называемый теорией Кокса [4; 5]. В ней деформируемое тело описывается весьма приближенно. Введенные впоследствии многочисленные дополнения и уточнения не смогли существенно улучшить эту теорию.

Применяемая в данной работе постановка, несомненно, имеет ограничения по интенсивности внешнего воздействия. Однако, границы ее использования достаточно широки и, как отмечается в [6], она применима для исследования внешних импульсных воздействий при давлении до 105 атм. Тем более, как отмечено в [7], при кратковременном воздействии конструкционные композиционные материалы упруги вплоть до разрушения.

Простейшей моделью, используемой при динамических расчетах элементов конструкций, является одномерная схема (стержень или безграничный слой постоянной толщины и неизменной структуры) [8-10]. Обширную библиографию по задачам о распространении упругих волн в стержнях можно найти в работах [11; 12]. В статье [12], в частности, критически проанализирована эволюция расчетных схем, обсуждаются пределы применимости различных теорий. Следует отметить, что наиболее изученным является процесс распространения волн в однородных средах.

Вопросы проверки откольной прочности однородных стержней конечной длины при продольном нагружении рассматриваются в статье [13]. Несущая способность проверяется по первой отраженной волне.

Однако, рассмотрением одномерных задач, имеющих, кстати, непосредственное отношение к конструкциям большей размерности, исследования не ограничиваются. Вообще, увеличение размерности, как и появление неоднородностей, значительно усложняют задачи расчета. В задачах расчета в этом случае превалируют статические модели упругих тел, как правило, несколько уточненные. Применяемые статические модели весьма разнообразны [14]. В ряде работ теории пластин и оболочек уточняются приближенным учетом тех или иных эффектов, связанных с тол- 23⁴   щиной. Во многих работах для описания процес-

Том 5

сов распространения волн используется теория типа Тимошенко [16-24]. Проверка последней и является темой данной работы.

Решение задачи

Для решения поставленной задачи воспользуемся обозначениями и результатами наших работ [1; 2; 25]. Отметим, что в этом исследовании предполагались нулевыми деформации поперечного сдвига. Приближенно учтем поперечный сдвиг, например, следуя предложению С. П. Тимошенко. Для кинематических переменных имеем:

z

W ( x , y , z , t ) = f е dz + W o ( x , y , t )

z        zz zz dr        d W.

U ⁽ x , y , z , t ) = J Y>^- J f— dzdz —— z + U ₀ ⁽ x , y , t ) = '          5 x        9x

H z z                                z z

— dzdz + |y„--0 I z + U =-  — dzdz + 9,z + Uo xz                       о                              x         о

₀₀dx       V      d x )           do^x

z      z z dr      d W

V ( x, y, z, t ) = J Y yz dz - J J— dzdz ——⁰ z + V ( x, y, t ) = dy      dy

0 0

zz

= -ff— dzdz + 1 1 Sy

Y yz V

d W Sy

^{z + V} 0

zz

= -[ [—dz+z + 0 z + V y0

0 0 y

Здесь W 0 , U ₀, V 0 - двумерные нестационарные перемещения точек поверхности приведения, за которую выбрана нижняя лицевая плоскость пластины (при z = 0).

По закону Гука и остальным соотношениям Коши будем иметь:

о

x

= C 11

zz 2

« - [ [ — dzdz W дx ²

zz

д0

д U

дx    дx

> dzdz +

^{+ C} 12

-и

0 0

dzdz ду у

д0

д V,

ду    ду

> dzdz

. d U д д , z +--0 > dzdz + dx

П \\S2^- Д Д , 50, ст = С„ < -  —ddddz + —- y 12 J JnSx2           dx

^T xy

⁺   22

^- ff

0 0

d 2 8

dzdz d y²

S0„ d И

+ y z +⁰ dzdz >

d y

9y

С⁵ e

° z = C 13 i- l I ТГ ^{dzdz +} n n d x

zz

zz

Г5 e

^{+ C} 23 IJ J d ; z--⁺- ⁺

I 00 5 У

zz

59,    d U_o   , ,

—- z + —⁰ >  dzdz +

d9 y d y

dx d V ■ z + —-0

d y

d x

> dzdz + C _{3 3}{e}

H S E . .

—- ^{dzdz +} 9xdy

d9

d U

d V

-+ + ^ 1 +-- ⁰ + —° ^ dzdz

^9y   dx )   9y   9x

Два оставшихся соотношения закона Гука следует записать с учетом введенной гипотезы о деформациях поперечного сдвига:

γ= ^{1 τ xz} dz или z θ= ^{τ xz} dz - z ^{∂ W 0 xz h ∫} 0 ^G xz              ^{nx ∫} 0 ^G xz       ^{n ∂ x}

1 ^{h τ} yz                       ^{zn τ} yz          ∂ W

γ=      dz или z θ=     dz - z ⁰

^{yz h ∫} 0 ^G yz             ^{ny ∫} 0 ^G yz       ^{n ∂ y}

Из уравнений равновесия найдем с учетом вышенаписанных равенств:

z

^т xz ( ^x , У , z , t ) = j -P

z

z     ^2

⁺J ^P 772 - C i i L ^d t

; 2

0 L a2 ax2

a ³          a³                   a³

-^ + C„ -dT + (Cn + 2 C44) -Ц axat2     11 dx3      12      44 dxay3

-

C44     (Uo + z9x )dz + dy

z

⁺ j —^{( C} 12 ^{+ C} 44 )

0 L

a ²

d x d y

V o + z 9 y ) dz + <

z

^T xz ^{( x} , У , z , t ) = J ^-P

0 _

z

z z jje dzdzdz +

_ oo

a ³         a³                   a³

----. + C„ _: ■ ( C_n + 2 C ₄)----. dxdt ^{2     11} ax^{3      12      44} дхду²

z z jj edzdzdz + f.0

z a²        a²

+j P^ — C 11      C(U 0 + z ⁹ * ) dz +

' _ a t       ax       ay

! 2

, 2

a-

0 _

+

z

J -( C 12 + C 44 )

0 _

d ² axay

( V + z 9 y ) dz + t 0 z

z

^T yz ⁽ x , У , z , t ) = j -P 0 _

a ³ a³                   a³

+ c ₂₂ -^+( c ₁₂ + 2 C ₄₄)

ayat2      ay3               ax 2ay

z z jj £ dzdzdz + J 00

z

⁺ j -^{( C} 12 ^{+ C} 44 ) 0 _

a ²

dxdy

(U 0 + z 9 x ) dz +

z

z 2

⁺ j ^P at^{2 -} C ^z n     at

0 _

a ² ax²

-

_ a ² ,        „ ..

c 22 ТГ (V 0 + z 9 y ) dz + T dy

yz

z2z о z (x, y, z, t) = fp -y fedzdz + 0  d t 0

zz

+ jj p 0 0 _

(  a4

a ⁴

vdx2 dt2   dy2 dt2

—2( C 12 + 2 C 44 )

a ⁴

ax²ay ²

a ⁴

¹¹ ax⁴

—

a ⁴

²² ay⁴

—

z z jje dzdzdzdz +

_ 00

z a2

+jpW0dz + 0  d t zz

+Ш

1 00 L

—

p— Тл + C 11 777- + ( C 12 + ² C 44 ) axat      ax

a1

d x dy ² _

( U_o + z 9_X) dzdz f +

zz

+UI

. 0 0 _

—

P^ + C 22 .   ■ ( C 12 + ² C 44 )

d ydt       d y

a3

d x² ay _

( V_o + z 9_y) dzdz f +

+σ

z

-

∂τ⁰ xz _z

∂ x

-

∂τ⁰ yz _z

∂ y

KI/IE АППАРАТЫ Ш

№ 4 (38) 2021 Том 5

При расчете пластин со свободной нижней поверхностью и с верхней поверхностью, нагруженной импульсом внешнего давления F ( x , y , t ), в разрешающую систему уравнений прикладной теории входят следующие зависимости:

а) граничные условия на нижней и верхней лицевых поверхностях пластины:

h j—p

0 L

d ³ 9x 91²

—

T 0 = От⁰ = Ga⁰ = 0 xz        yz         z

33 C 11ТГ + ( C 12 + 2 C 44 ) dx             9x 9y

zz jj £ dzdzdz +

J/0

h 22

d д       „О

⁺J ^{P       C |}1 Д 2   ^C 44 д 2 ^(U 0 ⁺ z ⁹ x ) ^d z ⁺

* L d t       9x       9y

9y

h Г

⁺ j ^{—( C}12 ^{+ C} 44 )

0 L

h i—p

0 L

h

a ³ 9y 91 ²

9x9y

(V + z 9 y ) dz = 0

+ C 22 ^    ■ ( C 12 + 2 C 44 )

9y             9x 9y

z z jj £ dzdzdz +

J 00

⁺ i ^{—( C}12 ^{+ C} 44 ) 0 _

a ²

9x9y

(U о + z 9 , ) dz +

h 2

⁺ i ^P 9? ^{— C} 44

0 L   ^ut

9x ²

—

C 22      (V o + z 9 y ) dz = 0

d y

h      2z jp -2 jedzdz +

0 ^d t 0

—2( C 12 + 2 C 44 )

hz jj p 0 0 _

a ⁴        9 ⁴

d x 2 91²   9y ²91²

—

C dL

¹¹ a x⁴

—

C dL

²² 9y⁴

—

dx 2 9y ²

z z

JJ e dzdzdzdz +

_ 00

h d ²  ,

⁺jp .2 ^dz W 0 ⁺

0 t

hz

+Ш

. 0 0 - hz

+Ш

—

93        9                  9

P---- +C C l     ■ ( C 12 + 2 C ₄4) — у

9x9t ^{2      11}9x^{3      12      44} 9x9y²

(U_o + z 9_X) dzdz f +

—

. 0 0 -

9 ³          9

P    ,  ■ C 22        ( C 12 + 2 C 44 )

dy 912       9y3

d

dx 2dy

(V_o + z9_y ) dzdz > = F ( x,y, t )

б) физические соотношения:

h

z

fi —p 0 ^ xz 0 L

hz

0 xz 0 l hz

0 xz 0 l

h

z

a ³

9x 912

+ Cu   + (C,2 + 2C44) —— dx             dx 9y

jj £ dzdzdzdz +

J 00

—

d x ²

x  a2

„   9 ² "_{z           x} ,

C44     (U0 + z9x)dz + ay

9x9y

. aw.

(V + z 9 y ) dz — h W = h 9 x

hz

I I-p

0 yz 0 -

a ³ 9y 91²

+ C22 -y + (C12 + 2 C44) — dy             9x 9y

z z jj £ dzdzdzdz +

J 00

h

z

h , z

⁺J7^J ^{( C} 12 ^{+ C} 44 )

0 yz 0 -

d ²

9x9y

(U 0 + z 9 x ) dz +

hz

’ ^a2

⁴⁴ 9x²

-

9'

C^    (V + z 9v) dz - h —⁰ = h 9

²² 9y^{2          y} 9y

y

в) соотношения, уравнивающие поперечные нормальные напряжения, найденных из уравнений равновесия (4) и определяемые законом Гука (2):

= r

z      2 z

J^p—J ^e dzdz ⁺

0 ^d t 0

—2( C_n + 2 C 4 ₄)

zz

+Ш

. 0 0 - zz

+Ш

—

zz

JJ p

0 0 _ d4

dx 2cy2

d ⁴        d ⁴

dx 29 t2   dy 2d t2

—

44 r —Г —- ¹¹ dx^{4     22} dy⁴

% \                \  92

J J e dzdzdzdz + J p — yZW₀ +

0' d t^{2      0}

_ 0 0

P^ + ^C”    ( C 12 + ² C 44 )

дx д t2      дx3

—

. 0 0 -

—

д'

дx дy2

33    3

p '. ■ C22     ■ (C12 + 2 C44) -д— дyдt2     22 дy3      12      44 дx 2дy

zz 2

< Д J — dzzdz +

x

(Uo +z0,)dzdz U

(V +z0y)dzdz - =

de,    9 U_o   _

—- z + —⁰ ^ + C

9x    9x

• 23 "

ff d²^.  de ,    9V I _ _M

-JJ 2 d ^{dzdz +} ^T z ⁺     Г ^C 33 ^{e}

0Л 9y       9y    9y

Начальные условия имеют вид:

9W 9U 9V t = 0W = 0 ^W = 0U = 0 ^U = 0V = 0 ^V = 0

9t

91

91

Рассмотрим, например, локальное поперечное нагружение безграничного слоя. В этом случае решения можно искать, воспользовавшись экспоненциальным преобразованием Фурье по продольным координатам:

∞∞

e(а, в, z, t ) = — j j s( x, y, z, t ) e^i^{ш -} i ^eY dxdy π -∞ -∞

∞∞

e( x, y, z, t ) = — j j е(а,в, z, t ) e i “ x ⁺ i ^₽Y dad в π -∞ -∞

В отмеченных соотношениях проведем интегральное преобразование Лапласа-Карсона по времени (р - переменная в преобразовании) и прямое преобразование Фурье. Трансформанты соответствующих функций отметим чертой сверху. Обозначим для краткости:

5 1 =а[р p ² + С _на ² + ( C 12 + 2 C 4 ₄)Р 2 ] 5 2 =р[р p ² + ( С 12 + 2 С 44 )а ² + С 22 Р ² ] Г = а5, +Р5₂

Тогда основное уравнение (8) можно записать в виде:

zz

zz zz

z

∫ ρ p ² ∫ ε dzdz - ∫ ∫ Г ∫ ∫ ε dzdzdzdz + ∫ ρ p ² dzW -

00 zz

00  00

zz

- i ∫∫ δ( U + z θ) dzdz - i ∫∫ δ( V + z θ) dzdz =

zz

= C _Зё + С ₁₃<

а ² j J s dzdz + iaz 0 + ia U_o > +

00 00

zz

+ C ₂₃ Ь² j J s dzdz + i p z 0 + i p V_o >

I 00 00                           y               J

Получили интегральное уравнение относительно е с разрывными подынтегральными функциями. Для его решения проведем преобразование Лапласа-Карсона по координате z ( s - переменная в интегральном преобразовании) и учтем отмеченное в [1]. Получаем систему равенств:

0СМИЧЕСН1/1Е АППАРАТЫ И

Том 5

-

+ W

P i Р p

- ^iU o

-

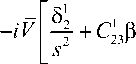
- i 9 ,

-1 +    3

ss

— i ⁹ ,

82/Ч'- s ³ s

= 0

f - ( C 3 a ² + C >в²)

+W o

^{- iV}0

-

— 42

zk - 1 z

J J b dzdz

z k — 1

да

( Г k -1

—

S ³

s ²

k

'33

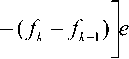
^- sz k - i

?             F.

;              s

z k — 1

s

—

e

, - ^sz ? - 1

ik

—

-

-

e

,^{— Sz} k — 1

s

s

t k — 1

S 5

' 33

iU 0

s

-

C ) e

-

C *"' ) e- sz?- i 0 ,  (8 ?

-

, , / 1           7          1

S z

s

s

e

,^{- sz} 1

-

tk

-

e

,^{- sz} ? - 1

Данная система уравнений решается последовательно. Из нее определяются трансформанты поперечной нормальной деформации ε _j ( α , β , s , p ) для каждого слоя композиционной пластины. Обращение по поперечной координате удается провести аналитически. В частности, для первого слоя получим:

—

y

-

—

-

Здесь λ ^j и λ ^j – положительные корни биквадратного характеристического уравнения:

Их, как показано в [2], возможно представить рядами Лорана, построенными в окрестности бес- конечно удаленной точки (что позволяет точно провести обращение и по второй координате):

Таким образом, волны расширения распространяются со своей обычной скоростью:

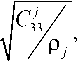
т. е. ρ конечно. Волны сдвига сливаются в одну и распространяются с одинаковой (в пределах слоя) бесконечно большой скоростью. При известных их скоростях, следовательно, необходимо принять:

G xz → ∞ и G xy → ∞.

Этот эффект является прямым следствием гладкой аппроксимации. Тогда, в соответствии с принятым интегральным физическим законом, γ xz ≡ 0 и γ yz ≡ 0.

Заключение

Рассмотрена возможность уточнения применяемых волновых теорий приближенным учетом поперечных деформаций сдвига. Показано, что применение интегрального физического закона приводит к противоречию. Отмеченный закон требует непрерывности касательных напряжений, а она, в свою очередь, в волновой задаче предполагает бесконечно большую скорость распространения волн сдвига. Это означает, что модули поперечного сдвига бесконечно велики. Выход из этого (предполагая конечность сдвиговых напряжений): ²³⁹ принять деформации сдвига нулевыми (или использовать не интегральный физический закон).