Волновое уравнение - НЕ уравнение электромагнитной волны

Показывается, что волновое уравнение только в первом приближении можно считать уравнением электромагнитной волны, и для нее предлагается новое уравнение, которое также следует из системы уравнений Максвелла. В этом уравнении демонстрируется строгое соблюдение закона сохранения энергии, сдвиг фаз между электрическими и магнитными напряженностями, преобразование энергии из магнитной в электрическую и обратно, закрученность электромагнитной волны.

Прежде всего заметим, что система уравнений Максвелла (СУМ) является системой дифференциальных уравнений и поэтому может иметь множество правильных математических решений. Среди них могут быть такие, которые соответствуют экспериментам и физическим законам, и такие, которые противоречат экспериментам и физическим законам. Волновое уравнение – из числа последних.

Решение СУМ для вакуума должно

• 1.    не противоречить закону сохранения энергии в каждый момент времени , т.е. устанавливают постоянство плотности потока электромагнитной энергии во времени,

• 2.    демонстрировать сдвиг фаз между электрическими и магнитными напряженностями,

• 3.    демонстрировать преобразование энергии из магнитной в электрическую и обратно,

• 4.    объяснять закрученность света , т.е. появление орбитального углового момента, при котором поток энергии не просто летит вперед, а крутится вокруг оси движения.

Рис. 1.

Однако решение в виде волнового уравнения

• 1.    противоречит закону сохранения энергии, т.к. в нем поток энергии изменяется во времени и сохраняет свою величину только в среднем , что в принципе нельзя считать соблюдением закона сохранения - см. рис. 1;

• 2.    демонстрирует синфазность электрической и магнитной напряженностей — см. рис. 1;

• 3.    не объясняет закрученность света,

В [1] найдено решение уравнений Максвелла для вакуума в цилиндрической системе координат {г, (, z], которое имеет следующий вид:

Hr. = hr(r)co,(1)

Нф.= hp(r)si,(2)

Hz .= hz(r)si,(3)

Er. = e/r^i,(4)

Ep. = ep (r)co,(5)

Ez.= ez(r)co,(6)

где co = cos( atp + xz + tot),(7)

si = sin( dtp + xz + tot),(8)

x = toV^C,(9)

ez(r) = 0,(10)

hz(r) = 0,(11)

er(r) = ep (r) = 0. 5Лг(й-1), A - const,(12)

ht(r) = J|er(r),(13)

hr(r) = -J|er(r),(14)

Л, а, w - const.

Эта же система уравнений в прямоугольной системе координат
{х, у, z} имеет вид
Ех = exsin((a + 1)ф + xz + wt),	(15)
Еу = eycos((a - 1)ф + xz + wt) ,	(16)
Н = h х cos( ( a + 1)<р + xz + wt),	(17)
Ну = h у sin((a - 1)<р + xz + wt),	(18)
где
ex ( r ) = е у ( r ) = 0.5Лг(a-1) ,	(19)
h х (r) = h у (r) = —J | e x ( r) ,	(20)
Г = ^x2 + у2 ,	(21)
ф = arctg(y/x) .	(22)

В этих решениях

• •    плотность потока энергии вдоль координаты Z на каждом радиусе Г сохраняет свое значение в каждый момент времени – соблюдается закон сохранения энергии,

• •    геометрическим местом точек равной напряженности (магнитной или электрической) на каждом радиусе является спираль – см. рис. 2

• •    наблюдается сдвиг фаз между электрическими и магнитными напряженностями– см. рис. 3,

• •    наблюдается закрученность электромагнитной волны – см. рис. 4.

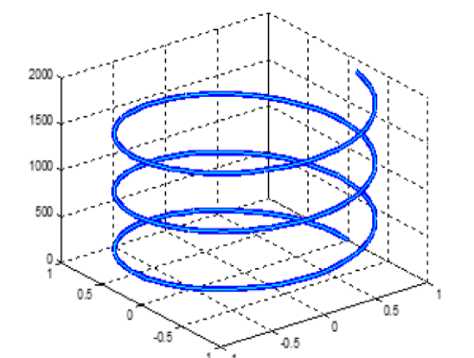
Рис. 2.

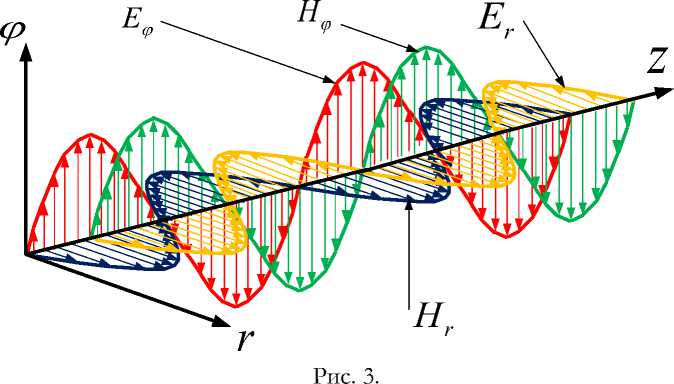
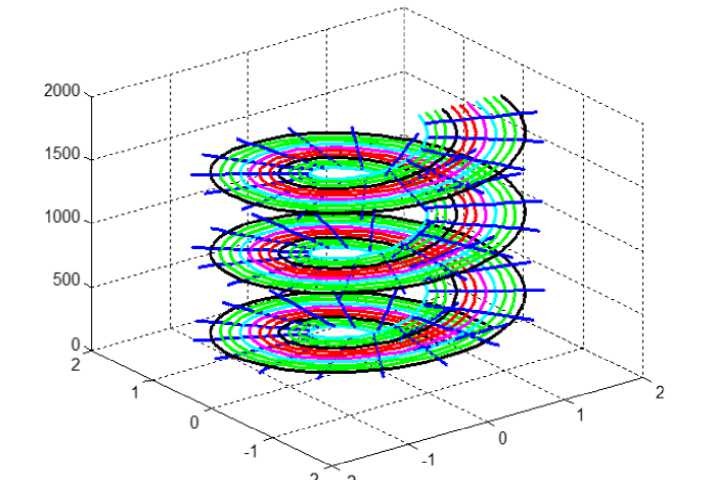
Рис. 4.

Рассмотрим еще сферическую систему координат ^{Р, в, Ф^} В этом случае решение уравнений Максвелла для вакуума в дальней зоне имеет следующий вид:

Еф = еф Kh(p, 6) sin(a р + хр + wt),

Ед = е9 Kh(p, 6) cos(« р + хр + wt),

Ер = 0,

Н ф = h ф Kh ( p, 9) cos( кр + ХР + cot), Н6 = h e Kh ( p, 9) sin( к р + хр + ot), Н р = о,

(26) (27) (28)

где Kh(p, 0) - определенная функция, вф, вд, Нф, Нд - константы, причем

НФ = J|e0,(29)

he = J^e^,(30)

Х = ^ТёД.

На рис. 5 показаны спирали — геометрические места точек, где плотности электрической напряженности при умножении на р остаются постоянными. Эти спирали лежат на конусе с углом 0 . Показаны несколько таких конусов.

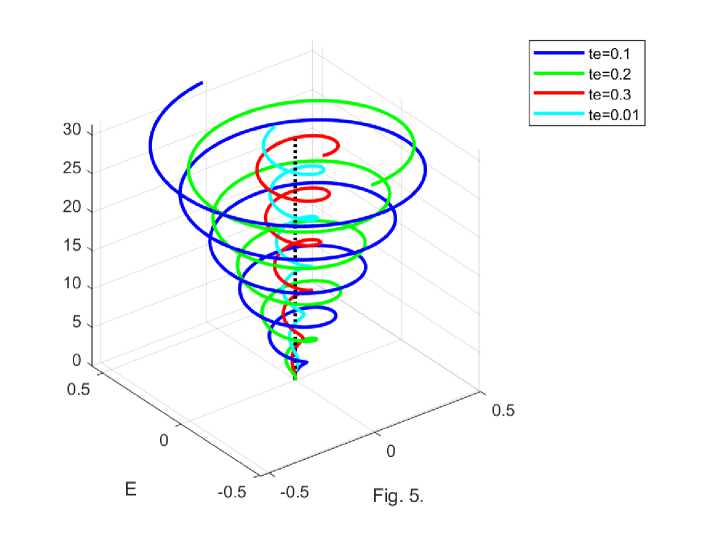
В этом решении

• •    плотность потока энергии, проходящего сквозь сферу, не зависит от радиуса и не зависит от времени , т.е. этот поток имеет одну и ту же величину на сферической поверхности любого радиуса в любой момент времени; иначе говоря, поток энергии , направленный вдоль радиуса, сохраняет

свою величину с увеличением радиуса и не зависит от времени, что соответствует закону сохранения энергии;

• •    наблюдается сдвиг фаз между электрическими и магнитными напряженностями;

• •    наблюдается закрученность электромагнитной волны.

Громадное количество теоретических выводов в электродинамике сделано на основе использования волнового уравнения. Эти выводы получены с нарушением закона сохранения энергии и с этим приходилось мириться. Теперь, когда найдено точное решение уравнений Максвелла, необходимо пересмотреть и уточнить ранее полученные результаты. Это необходимо потому, что некоторые результаты могут оказаться принципиально неверными (а не только ошибочными с некоторой погрешностью).