Волны в градиентно-упругой среде с поверхностной энергией

Wave propagation in homogeneous gradient-elastic media with surface energy is studied. Dispersion properties of longitudinal and shear waves, Reyleigh surface waves and SH surface waves were analized in linear approximation.

В последние два десятилетия в физике твердого тела, главным образом в материаловедении, получила признание концепция структурных уровней деформации [1,2]. Согласно этой концепции, каждая точка твердого тела представляет собой сложную систему взаимодействующих структур более низкого структурного уровня.

Но значительно раньше идея о структурных уровнях была сформулирована в механике сплошных сред при рассмотрении твердых тел с внутренними степенями свободы и восходит к работам В. Фойхта (1887,[3]), Е. и Ф. Коссера (1909,[4]), Леру (1911,[5]). -

Теория континуумов с микроструктурой по своим гипотезам занимает промежуточное положение между классической теорией упругости и физикой твердого тела, стоящей на позиции существования структурных уровней. Материальная точка в континууме с микроструктурой имеет “разумную” степень сложности, что позволяет описывать и структуру материала (это недоступно для теории упругости), и волны деформации (это недоступно для материаловедения).

В модели микроморфной среды Миндлина [6] предполагается, что для достаточно малого макроэлемента его движения состоят из параллельного переноса, вращения около центра масс и афинной деформации.

Один из вариантов среды Миндлина был рассмотрен Я. Вардолакисом и X. Георгиадисом [7]. Данная теория предполагает в выражении для плотности энергии деформации, помимо классических компонент, содержание дополнительных слагаемых: градиента деформации (Леру) и поверхностную энергию. Такая модель получила название градиентно-упругой среды с поверхностной энергией.

В настоящей работе рассмотрены особенности распространения различных типов упругих волн в градиентно-упругой среде с поверхностной энергией (объемных, поверхностных, SH поверхностных волн и SH волн в слое).

Основные уравнения

Рассматривается однородное пространство с микроструктурой. Положение каждого структурного элемента в этой среде определяет радиус вектор в декартовой системе координат Х|, Х2, хз. Предполагаем, что микросреда сливается с макросредой, р — масса микроматериала на единицу макрообьёма, микросреда является кубом с ребром длиной 2Л.

Для решения задачи используем следующий постулат для функции плотности энергии деформации, предложенный в [7]:                          .

• ^ = ^»^ ⁺ ^дАд +^_S£grId_se,J+klb_sd_s(_iEg_r£,.g),           (1)

где X и ц - стандартные константы Ламе, с- градиентный коэффициент (имеющий размерность [длина]²), b_s = b\_S) v^=l и где b есть длина материала, относящаяся к поверхностной энергии, Eq^Mlf^Uq^dqUr) - тензор деформации.

Последний член (1) относится к поверхностной энергии, поскольку в силу теоремы Гаусса - Остроградского, он может быть записан в форме

Jd_s (м^ V = ^b |(м«? \^_sn_s Ж

(s)

где J обозначает интегрирование по объёму V, J - интегрирование по поверхности (И(s)

S, охватывающей объем V, и »s - компоненты единичного вектора внешней нормали к поверхности.

Заметим, что положительная определённость плотности потенциальной энергии исходит из следующих ограничений на константы материала: (31+2р)>0,    р>0,    с>0,     -1 < (л-/с|/2)< 1.(2)

Коэффициент с зависит от размеров структурных элементов и находится как сД0,25А)2.(3)

Уравнения движения в напряжениях в отсутствии объёмной силы в случае гладкой границы записываются следующим образом:

dJv + а^)=р(д„мг),(4)

д^Лвга =|p^@ziV^(5)

где т_дг, a_qr, m_qr-- тензор напряжений Коши, тензор относительных напряжений и тензор двойных напряжений, ^дг- несимметричный тензор микросмещений.

Используя (2),(3) можно получить уравнение движения в перемещениях ри = ZV2U + (X + 2p)V2U + (х + ц - pcV2 jrotrotU - 2pcV4U .(6)

Продольные и поперечные волны

^*W*«_A -2цсиЛ1Х|Х;Х|

1 / 2

+ —р/? м^#

"Р^п = 0.

Решение (7) будем искать в виде бегущей гармонической волны и = Ае^№^^к^

где ^-волновое число, очастота.

Подставив (8) в уравнение (7), получим дисперсионное уравнение

(X+адк² - аде⁴ - ^к² + р)ю² = о,

где / = 1 / ЗрА2 -момент инерции частицы вещества.

Из дисперсионного уравнения можно найти явную зависимость частоты от волнового числа:

со = ^

с2 + 2сс2^2

1+1/3/?Ч2

(Ю)

где c_z =

--скорость продольной волны, с, =--скорость сдвиговой волны в

V Р                                     VP классической теории упругости.

На рис. 1 приведена зависимость частоты от волнового числа. При малых значениях волнового числа, когда размер зерна не важен, дисперсия отсутствует. В этом случае фазовая скорость — = с2 совпадает со скоростью продольной волны в классической упругой среде. При щ-^оо дисперсия также отсутствует и асимптотическое значение фазовой скорости

Рис. 1. Закон дисперсии продольных волн Рис. 2. Закон дисперсии поперечных волн

Уравнение, описывающее распространение поперечных волн, также получается из (6) при подстановке U = (0, v(xt ,/),0).

(И)

Аналогично, как и для продольных волн, находим дисперсионную зависимость частоты от волнового числа:

График закона дисперсии приведен на рис.2. Совпадение данной кривой с дисперсионной зависимостью, построенной по классической теории упругости, наблюдается так же, как и для продольных волн, при малых значениях к и ох В этом .                      0)— случае дисперсия отсутствует и фазовая скорость — = ст. При стремлении со к -                      .            .                   .                                                 к'

бесконечности фазовая скорость уменьшается и в пределе со -^ о» имеет значение:

Заметим, что в уравнении движения в перемещениях (6) нет слагаемых с параметром Ь. Скорости продольных и поперечных волн также не зависят от данного параметра. Поэтому дополнительное слагаемое в выражении плотности потенциальной энергии, отвечающее за поверхностную энергию, не влияет на распространение объемных волн в данной исследуемой модели среды.

Поверхностные волны Релея

Пусть полупространство занимает область хз >0, а оси декартовых координат х/ и хз направлены по поверхности.

Рассматривается плоская гармоническая волна, распространяющаяся в направлении оси х/, амплитуда которой экспоненциально уменьшается с расстоянием от свободной поверхности Х2. От нуля отличны две компоненты вектора перемещения Uxi”Ui(XbX2)» u_X2~U2(xbX2). Принимаем, что Ьх1-Ъ_хз~0, Ъ_Х2=ЬтЮ.

Условия на границе будут следующими:

o₂i (^i, х₂ = 0) = О      при -оо < ^ < о»;

°22(Х1 >х2 =0)                                     ^^

W22)(^>x2 =0)=0; .

т_П1^х_х,х₂ -0) = 0.

Разложим вектор смещений на потенциальную и соленоидальную составляющие:

U = gradф + roty, divy - 0.                            (14)

Поскольку волна плоская и движение не зависит от х3, у векторного потенциала будет отлична от нуля только компонента по оси х3: у = (0,0, Уз).

Применим сначала к уравнению (6) операцию div, а потом операцию rot. В результате получим следующую систему уравнений:

рф = 7У2ф + (Х+2ц)72ф-2цсУ4ф,(15)

■                     PV3 = ^2Уз + pV2y3-|Лс74ф3.(16)

Решение как (15), так и (16) будет состоять из двух убывающих от свободной поверхности компонент:

<р = ^"^ + S^* je^-^,(17)

V3 = \Cevy + ОГ» )^*, где к - волновое число, со-частота, Л, В, С, D- амплитудные функции, и а = ^ -z. , Р = 7^^ ■(19)

Величины z^2 являются корнями следующего уравнения:

2pcz2 + (x + 2p-7®2)z-po)2 =0,

Dis = (А + 2ц - 7со²)² + 8цсрсо, - А - 2ц + /со² ± -Tois

• 2- 2 _              -,

4цс

А также для \Цз:

р = 4k2 - с2 , q = ^к2 + т2 ,О = Щ-^ ,(20)

• V 2с

t”                                                     .(21)

V 2с у цц

Граничные условия, выраженные через компоненты вектора перемещения, будут следующими:

^21 (^и^ =0) = 7^712 +Ц (7/2,1 +^1,2)“ИС^ (^2,1 +^1д)?ПРИ ~°°<Х] < °0,

^22 (Х1 , -^ - 0) = ^2,2 + ^ (Ц,1 + ^2,2 ) + ^Ц^^ - 2ЦсУ2(/2 2 , w221 (^l > ^2 ~ 0) = Ц^ (^2,1 + ^1,2 ) + Е6‘ (^2,12 + ^1,22 ) ’

^222 (^15 -^2 — ^) — 2ц/^7/22^” 2ЦС бД 22 *

Подставляя (17), (18) в (14), а затем (14) в (22), получаем однородную линейную систему из четырех уравнений с неизвестными амплитудными функциями Л, В, С и D. Как известно, такая система имеет решение тогда и только тогда, когда ее определитель равен нулю. Данное условие и будет дисперсионным соотношением для волны Релея. Введем нормированные величины, с которыми в дальнейшем удобно оперировать:

k_d =к^, m_d = ®4="» V= = ™,               (23)

V3E у р Vc

Cd =oVc, Td =TVC, zdl2 ^zuc,cd где Cd -нормированная фазовая скорость.

Тогда

Pd = 4^kd-c"_d , q_d = jkd +T²_d , a_d = y^-, T_d = уЫ-,        (24)

• 5 =         X = l-(oL a_d=4k^^, ^_d=yl^-z_d2 ,

^ = 7---2 + ®d+ - + 2-to^ b--6)^ .

• ⁴ I-¹ VV^ ) ² J

Дисперсионное соотношение в нормированных координатах будет выглядеть следующим образом:

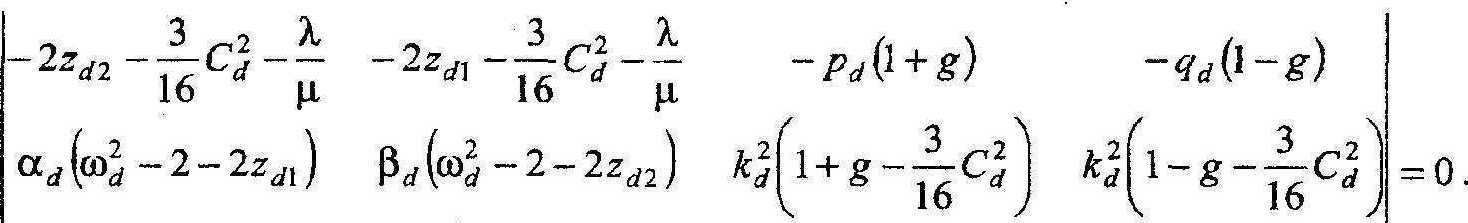
^d^d ~^а)        Р<у^_d -р^)      -k_dp_d^b_d -p_d)   -k_dq_d(b_d -^d)

-la>d-a^ -l^bd-^  ^ + p^b, -pd) ^^\ьа-Ч^

Дисперсионные кривые были построены для среды с упругими постоянными: Х=8-10⁹, ]Д=2,Ы0⁹. Параметр b_d принимал значения: ОД; 0,5; 0,75. Оказалось, что значения нормированной частоты и нормированной фазовой скорости для данной упругой среды при различных значениях bd близки друг к другу соответственно так, что дисперсионные кривые, приведенные на рис. 3 и рис.4 , сливаются в одну. Поэтому можно предположить, что введение дополнительного слагаемого в выражение плотности потенциальной энергии, отвечающего за поверхностную энергию, незначительно влияет на характер распространения плоской поверхностной волны Релея. На рис. 3, 4 приведены дисперсионные зависимости нормированной частоты и нормированной фазовой скорости от нормированного волнового числа при значении ^=0,5. -

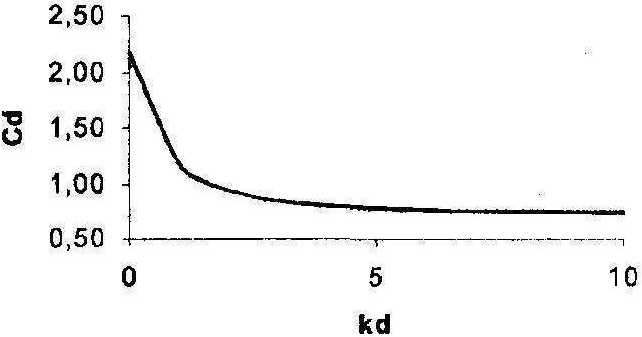
Рис.4. Дисперсионная зависимость нормированной фазовой скорости от нормированного волнового числа поверхностной волны Релея

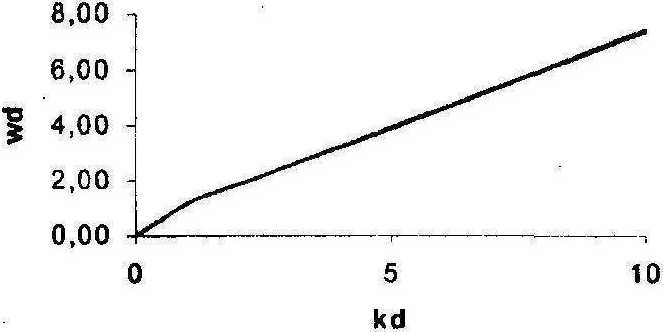
Рис.З. Дисперсионная зависимость нормированной частоты от нормированного волнового числа поверхностной волны Релея

По дисперсионным кривым можно сделать вывод, что скорость волны Релея зависит от частоты, т.е. имеет место дисперсия. Для материала с приведенными выше упругими постоянными при <о=О значение фазовой скорости Crg совпадает со значением фазовой скорости Crkh поверхностной волны Релея в классической теории упругости:

^ =—2,1746 = 0,9416, --^ = 0,9416.

С2 4С

Асимптотическое значение фазовой скорости при со —> °° для данного материала £5^ = 2^0,73 = 0,32.’

С2 4,

Сдвиговая анти-плоская поверхностная волна

Будем рассматривать неплоские сдвиговые (т.е. горизонтально поляризованные или SH) движения в градиентно-упругом полупространстве с поверхностной энергией. Этот тип волн уже рассматривался в [7]. Пусть в декартовой системе координат Ох_хх₂х₃ полупространство занимает область (-oo2>0) и оно достаточно толстое в направлении оси х₃, чтобы допустить неплоское сдвиговое состояние. В этом случае задача двухмерная и зависимость есть только от ^х_х,х_г).

Также примем, что b_x = b_z ~0,b_y ^Ь^О. Для настоящего случая SH- движений в полупространстве х₂>0 мы имеем U_x = U₂ = 0, U₃ = w(x_vX2,t)^^- Уравнение, описывающее SH волны, имеет следующий вид:

pV2w-pcV4w + 7V2w-pw = 0.                   (25)

Заметим, что уравнение (25) совпадает с уравнением для роторной составляющей поверхностной волны Релея.

Граничные условия в перемещениях:

а23 (х,, х2 = 0) = Ц№е - ncw21] - ^cw222 + Iw2 = 0, тт^хА,х2 =0) = pcw22 -p6w2 -0.'

Решение (25) состоит из двух убывающих компонент:

Ws^ ■ е”№ + В ^* ]■ е^^+к.с,(27)

где к - волновое число, to-частота, А и В - амплитудные функции, р и q удовлетворяют соотношениям (20) и (21).

Также в работе [7] получено дисперсионное соотношение

В нормированных координатах (23) из дисперсионного соотношения можно выразить волновое число через частоту kd =         +                        ■(29)

V 16 X V'

Заметам, что (29) выполняется не при любых cod. Начало диапазона действительных частот определяет частоту среза, которую можно найти из условия:

На рис. 5 отображена зависимость нормированного волнового числа от нормированной частоты, на рис.6 - зависимость нормированной фазовой скорости C_d =to_d { k_d от нормированной частоты.

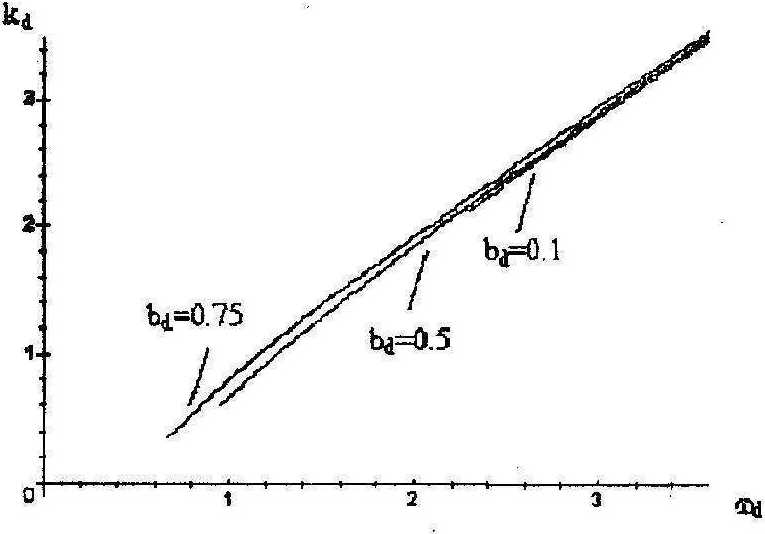
Рис.5. Дисперсионная зависимость нормированного волнового числа от нормированной частоты SH поверхностной волны

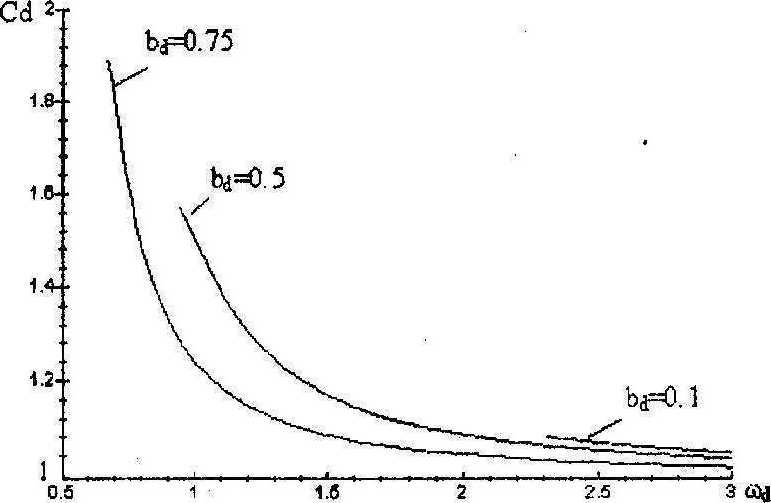
Рис.6. Дисперсионная зависимость нормированной фазовой скорости от нормированной частоты SH поверхностной волны

Для данной задачи дополнительное слагаемое в выражении плотности потенциальной энергии позволяет теоретически доказать существование SH поверхностных волн в полупространстве однородного материала. Экспериментально этот тип волн можно наблюдать, однако в рамках классической теории упругости они неопределяемы. Рассматриваемый случай является подтверждением эффективности слагаемого в выражении плотности потенциальной энергии, отвечающего за поверхностную энергию.

• • SH поверхностные волны в полупространстве однородного материала обладают дисперсией. Дисперсионное соотношение в нормированных координатах не зависит от материала, поэтому для всех материалов дисперсионные кривые будут подобны кривым, построенным выше. При о-э^о асимптотическое значение фазовой скорости C_SH равно: ' .

=2§ = 0,43.

С2 4

Распространение SH-волн в слое

Будем рассматривать анти-плоские волновые движения в слое, распространяющиеся в направлении оси x_t. Слой ограничен плоскостями х₂ = 0 и х₂ = d. Задача двухмерная, и зависимость есть только от (Xj ,х₂).

Также примем, что b_x = b_z = ^,b_y s b ^ 0. Для настоящего случая SH- движений в слое мы имеем: U_x =U₂ = 0, U₃ = w(x_1?x₂,/) * 0.                                 .

Уравнение движения будет тем же самым, что и в предыдущем разделе pV2w-pcV4w + /V2w-pvv = 0.                   (30)

Число граничных условий по сравнению с предыдущим случаем будет в два раза больше, поскольку появляется вторая граница х₂ = d.

Си (^, х₂ = 0) = gw₂ - fuw_M1 - Цси/₂₂₂ + /w₂ = 0, ^223 (^Х1 >^х2 = 0) = V^W^ - Ц^г ⁼ 0,

^2з(х1>х2 -^"^г "Pcw211 " 1^^222 + ^2 ~ ^’

^223 (^Х1 ’^Х2 ⁼ ^) " ^^,22 " ^^w,2 "  0.

Решение уравнения (30) будет состоять уже из четырех компонент:

w = [Л • sin(Py) + В cos(Py) + Csh(qy) + Dch^qy)V е¹^^-^^ -^к.с.,         (32)

где к - волновое число, со-частота, А, В, С и D- амплитудные функции, q удовлетворяет соотношениям (20) и (21), а

Р=4М?.                  (33)

Подставляя (32) в (31), получим линейную однородную систему четырех уравнений, решение которой существует при условии обращения в нуль определителя матрицы, составленной из коэффициентов в полученной системе при амплитудных функциях А, В, С и D. Раскрывая определитель и вводя нормированные величины (23), (24), получим следующее дисперсионное уравнение:

Iti^ О - cos(/% )сЛ(^)) + Sin(^ }^h\q.Y_d ) x

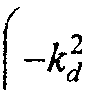
, 13 2

1--«£

4 I i 39 ₂    39 4           ,2 2 I n

+ <% ”I + 77«5-7T®^®ti*^^ =°=

где P_d = Pjc, Y_d=^. .

Дисперсионное соотношение в нормированных координатах так же, как и в предыдущей задаче не зависит от свойств материала. На рис.7 и рис.8 изображены зависимости нормированной фазовой скорости от нормированного волнового числа для параметров: b_d =0,5; d = 10Л ; b_d =0,5; d = 20/?.

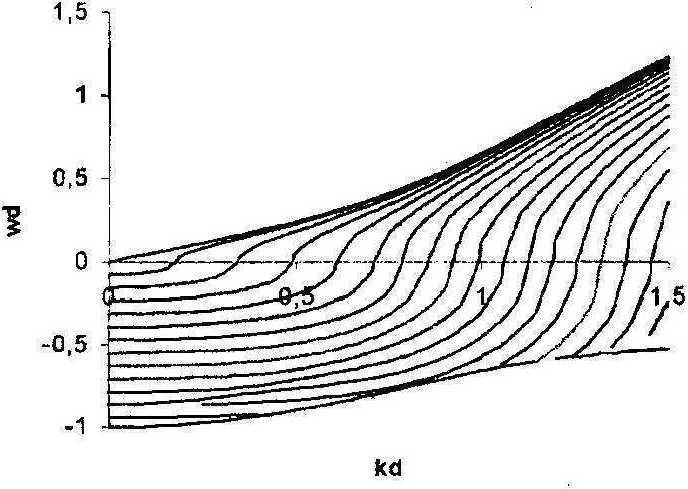
Рис.7. Дисперсионная зависимость нормированной фазовой скорости от нормированного волнового числа SH- волн в слое при значениях параметров b_d =0,5;^ = 10/z

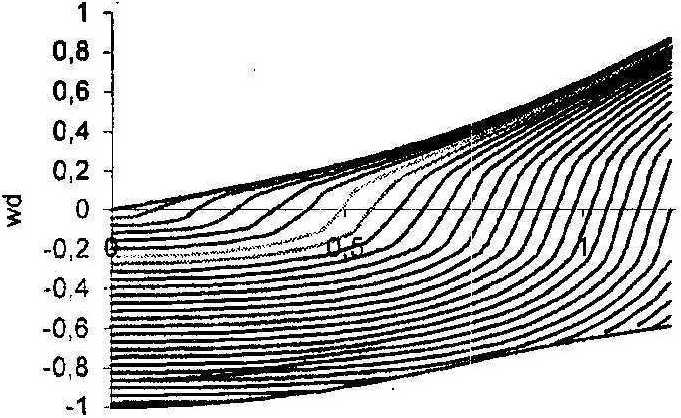
kd

Рис.8. Дисперсионная зависимость нормированной фазовой скорости от нормированного волнового числа SH- волн в слое при значениях параметров b_d =0,5;^ = 20Н

В заключение приведем таблицу, в которой отображены асимптотические значения фазовых скоростей для различных типов волн.

Асимптотические значения фазовых скоростей для различных типов волн

Тип волн	Классическая теория упругости	Теория градиентной упругости, учитывающая поверхностную энергию
Продольные волны	С1	0,61 ст
Поперечные волны	Ст	0,43ст
Поверхностные плоские волны		0,32ст (Х=8-109,ц=2,1109)
Сдвиговые анти-плоские поверхностные волны	Не существуют	0,43ст
Сдвиговые анти-плоские волны в слое	Ст	0,43ст

Работа выполнялась при поддержке Российского фонда фундаментальных исследований (грант № 00-02-173 37).