Вопросы динамики многодвигательного электропривода на примере механизма наклона конвертера

В настоящее время многодвигательным приводом (два, четыре и более) оснащены многие тяжелые машины и механизмы горнометаллургической отрасли, например кислородные конвертеры. Привод таких машин представляет собой разветвленную многосвязную систему валопроводов с суммированием моментов на общей шестерне. Такая схема позволяет уменьшить суммарный момент инерции механизма и снизить динамические нагрузки в передачах по сравнению с однодвигательным приводом и, следовательно, снизить их массу и габариты. С другой стороны, увеличение числа валопроводов приводит к появлению дополнительных механических связей и, как следствие, к росту зазоров в зубчатых передачах и несинхронности нагружения отдельных ветвей. Даже небольшие отклонения в значениях моментов инерции и жесткости валопроводов приводят к росту динамических нагрузок, колебательному характеру в нестационарных режимах работы (пуск, торможение, реверс) и возможному преждевременному отказу оборудования.

Анализу поведения многосвязных электроприводов посвящено значительное число публикаций. Результаты теоретических и экспериментальных исследований динамики многомассовых ЭМС рассмотрены в работах Кожевникова С.Н. [1], Большакова В.И., Буцукина В.В. [2–4], Ключева В.И. [5], Борцова Ю.А., Соколовского Г.Г. [6].

Настоящая работа посвящена исследованию поведения электромеханической системы многодвигательного привода механизма

наклона конвертера в типовых режимах работы с целью определения путей локализации узлов, требующих ремонта.

Уменьшение влияния недостатков, характерных для разветвленной многосвязной системы, возможно за счет создания систем регулирования на основе математических моделей рассматриваемых электромеханических систем (ЭМС). В полной математической модели учитывается число электродвигателей ЭМС, зазоры в передачах, упругости валопроводов, влияние диссипативных сил и т.д. Недостатком такого подхода является сложность таких моделей. Это приводит к большим вычислительным и временным затратам при их реализации, что зачастую недопустимо в реальных условиях производства.

Для анализа динамических процессов, возникающих в режимах разгона и торможения электромеханической системы механизма наклона конвертера, предлагается использовать упрощенную эквивалентную расчетную модель, которая учитывала бы изменение собственной частоты колебаний ЭМС для любого режима работы на основе технологических и конструктивных особенностей. На основании анализа расчетной модели сделан вывод о необходимости оценки механических нагрузок в системе методом сравнения их текущих и базовых значений, а также учета демпфирующих свойств электропривода. Для предварительной оценки динамики рассматриваемой системы с помощью программного пакета Matlab Simulink выполнено моделирование процесса разгона.

I ГОРНЫЕ НАУКИ

I Ж И ТЕХНОЛОГИИ

2020;5(3):253-265

МИСиС

Национальный исследовательский технологический университет

Поскольку анализ текущих сигналов, поступающих от системы электроприводов, не позволяет оценить ее техническое состояние, предлагается использовать данные, полученные в результате термо- и вибродиагностики.

Расчетная схема ЭМС многодвигательного привода наклона конвертера

Для многодвигательных электроприводов, содержащих два, четыре, шесть и более приводных электродвигателей основным недостатком является различие в кинематических зазорах по каждому из валопроводов. При пуске такой сложной ЭМС будут наблюдаться участки, соответствующие выбору зазоров по каждому из валопроводов. На приводимых ниже осциллограммах (рис. 1) хорошо прослеживается неодновременность пуска валопроводов четырехдвигательного привода механизма поворота и появление параметрического резонанса в районе половинной частоты вращения (на 11-й секунде) при пуске и в случае реверса

на 41-й и 51-й секундах. В качестве регистрируемых величин приняты упругие моменты по каждому из валопроводов (первый – четвертый), а также частота вращения и ток первого двигателя. Неодновременность выбора зазоров видна на характере изменения упругих моментов – M 121 , M 122 , M 123 , M 124 .

Число приводных двигателей может достигать 10–16. При таком числе приводных двигателей приемлема их группировка в блоки по два или четыре, а также необходимость чередования блоков с последовательным и параллельным соединениями машин.

Нагрузка на двигатели у механизмов поворота и кантования будет усредняться в установившемся режиме движения, в пускотормозных режимах из-за различных условий выбора зазоров, нагрузка на отдельные двигатели может возрастать более чем в 2 раза, аналогичная ситуация повторяется и для упругих моментов в валопроводах [5, 6].

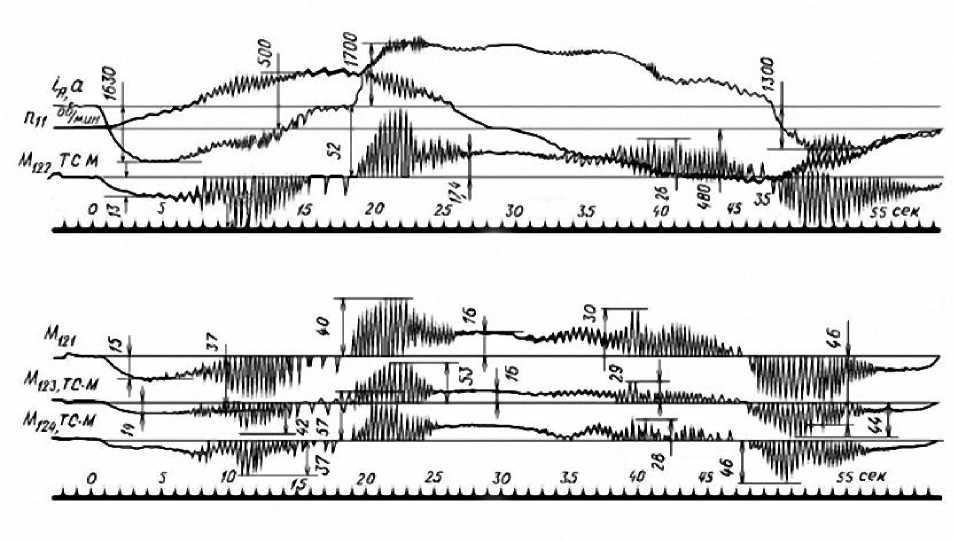
Рис. 1. Осциллограммы пуска четырехдвигательного привода механизма поворота: i я – ток якоря электродвигателя; n 11 – частота вращения 1-го электродвигателя;

M 121 , M 122 , M 123 , M 124 – упругие моменты валопроводов (с 1-го по 4-й)

Fig. 1. Oscillograms of starting the four-motor drive of the tilting mechanism: i a – electric motor armature current; n 11 - speed of rotation of the 1st electric motor; M 121 , M 122 , M 123 , M 124 – elastic momenta of shafting (from the 1st to 4th)

2020;5(3):253-265

а

б

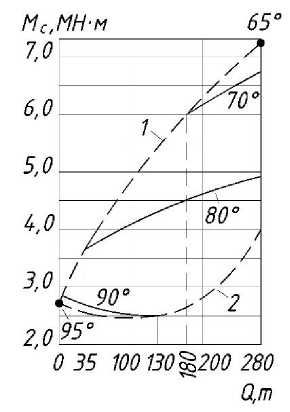
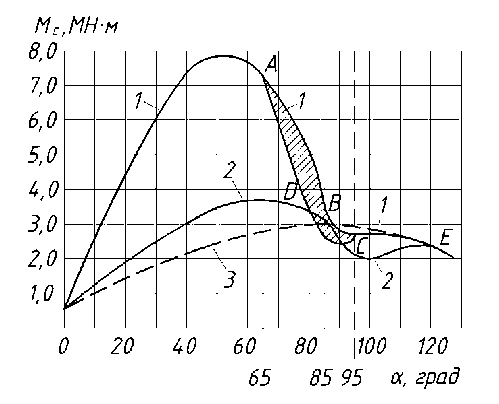
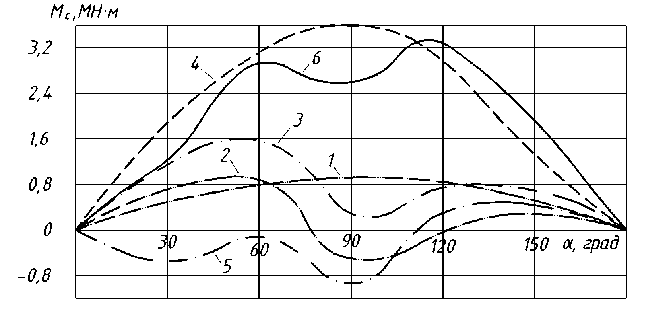
Рис. 2. Зависимости статических моментов на цапфе от количества металла в конвертере ( а ) и в функции угла поворота α конвертера ( б ):

на а : 1 – граничная кривая, соответствующая появлению шлака в сталевыпускном отверстии; 2 – граничная кривая, соответствующая началу слива шлака через горловину конвертера;

на б : 1 – слив стали; 2 – возврат в исходное положение с 44 т шлака; 3 – поворот порожнего конвертера; 65° – начало слива стали; 85° – начало слива шлака через горловину; 95° – окончание слива стали; 120° – окончание слива шлака

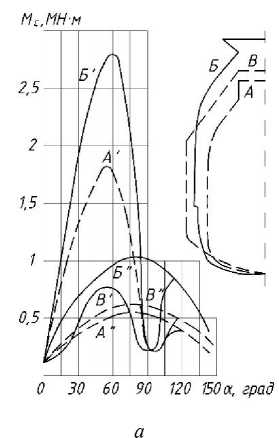
Fig. 2. First momenta on the trunnion as a function of the amount of metal in the converter (a) and as a function of the converter tilt angle α (b)

in ( a ): 1 – boundary curve corresponding to appearance of slag in the steel-tapping hole; 2 – boundary curve corresponding to the beginning of slag pouring through the converter mouth;

in ( b ): 1 – steel pouring; 2 – return to initial position with 44 tons of slag; 3 – tilting empty converter;

65° – start of steel pouring; 85° – start of slag pouring through the mouth; 95° – finish of steel pouring;

120° – finish of slag pouring

б

Рис. 3. Зависимость статического момента на цапфах конвертера 250 т от профиля конвертера ( а ) и угла его поворота ( б ) :

А', Б', В' – загруженные конверторы с садкой 125 (А), 190 (Б) и 230 (В), т; А", Б", В" – то же для порожних конверторов; 1 – момент порожнего конвертора с новой футеровкой; 2 – момент от садки в конверторе с новой футеровкой; 3 – суммарный момент при новой футеровке; 4 – момент порожнего конвертора с выгоревшей футеровкой; 5 – момент от садки в конверторе с выгоревшей футеровкой; 6 – суммарный момент при выгоревшей футеровке

Fig. 3. Dependence of the first moment on the 250-t converter trunnions on the converter profile (a) and its tilt angle (b):

A', B', C' – loaded converters with load 125 (A), 190 (B) and 230 (C), t; A", B", C" – the same for empty converters; 1 – moment of empty converter with new lining; 2 - moment due to the load in converter with new lining; 3 – total moment at new lining; 4 – moment of empty converter with burnt-out lining; 5 – moment due to the load in the converter with burnt-out lining;

• 6 – total moment at burnt-out lining

  2020;5(3):253-265

Момент сил сопротивления Мс меха-      валопроводов, характер изменения моментов низма наклона конвертера существенно изменяется в процессе отработки технологических операций [7-9]. Одновременно с изменением Мс наблюдается и изменение приведенного момента инерции:

J = m р², где m - полная масса металла и собственно конвертера, р - радиус инерции.

Это очевидно, так как в процессе наклона изменяется положение центра тяжести. Наибольшие значения J (ф) будут иметь место в случае выгоревшей футеровки по сравнению с показателями для новой футеровки. Зависимость для J (φ) будет в некоторой степени повторять кривую М с (ф). Характерные зависимости момента сил сопротивления от состояния футеровки и угла наклона конвертера для различных садок приведены на рис. 2; влияние профиля конвертера на момент привода механизма наклона и зависимость М с (ф) для Q = 250 т - на рис. 3.

При анализе исследований по динамике привода наклона конвертера [2–4] было замечено, что основной упор делался на изучении нагрузок в валопроводах от тихоходного редуктора к венцовой шестерне, а также склонности электромеханической системы к биениям. В качестве расчетных схем принимались эквива-

лентная двухмассовая и многомассовая, в которых моделировалось изменение времени приложения движущего момента к рассматриваемым

валопроводам, учитывался процесс растормаживания приводов [1, 5, 10]. Реальная расчетная схема должна учитывать систему электропривода, схему соединения электродвигателей, основные жесткости, зазоры по линии каждого из

сопротивления М с (φ) и инерции J конв (φ) при наклоне конвертера [11]. Особенно следует выделить зоны с минимальными и максимальными значениями М с и J конв . При упрощенном моделировании ЭМС наклона возможно задание механической характеристики двигателя в графическом виде или таблично [12, 13]. Типовая схема шестидвигательного одностороннего привода механизма наклона конвертера приведена на рис. 4.

При пуске многодвигательного привода механизма наклона конвертера наблюдается неодновременное подключение приводных ветвей к венцовой шестерне [3, 14, 15]. При этом возможно рассмотрение нескольких типовых случаев, к числу которых следует отнести: 1) подключение одной приводной ветви к венцовой шестерне в первый момент; 2) одновременное подключение двух приводных ветвей и 3) подключение оставшихся валопроводов к венцовой шестерне после выбора зазоров.

В первом случае [16] собственная частота колебаний может быть найдена как

^ 12 =

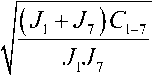
Подключение второго валопровода приведет к изменению собственной частоты

,» _   ⁽ J 1 + J 2 + J 7 ⁾⁽ C i - 7 + C 2 - 7 )

V        ⁽ J 1 + J 2 ) J 7

В случае подключения всех валопроводов к венцовой шестерне собственная частота ЭМС наклона, приведенная к двухмассовой, находится из выражения

_хт _   ^{( C} 1 - 7 + ^C 2 - 7 + — + C 6 - 7 ⁾⁽ J 1 + J 2 + — + J 6 + J 7 )

\              ⁽ J 1 + J 2 +   J 6 ) J 7

Рассмотрим отношение собственных частот колебаний:

⁽^1 2 ) _       ⁽ J 1 + J 7 ) C 1 - 7 ⁽ J 1 + J 2 ) ^J 7

( Q‘2 )    ^J 1 ^J 7 ^{( J} 1 + ^J 2 +^ + ^J 7 ^{)( C} 1 - 7 + ^C 2 - 7 )

2020;5(3):253-265

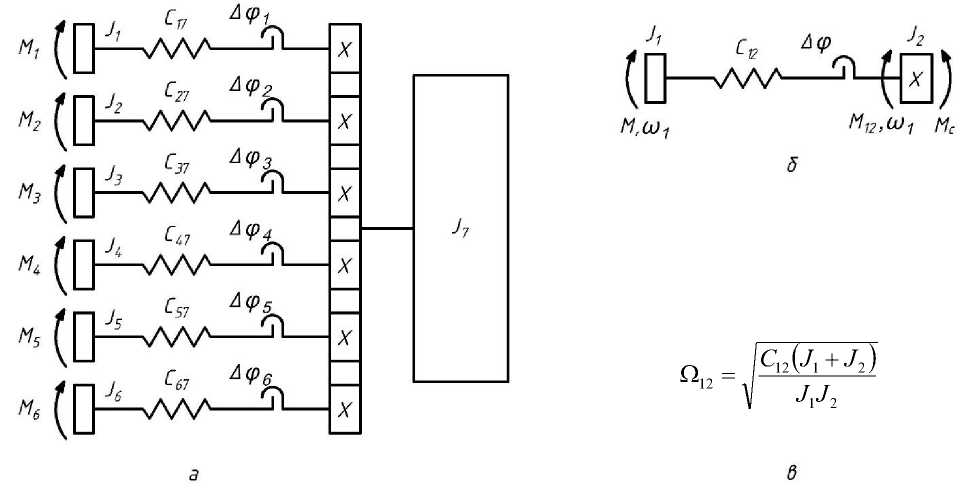
Рис. 4. Расчетная схема механизма наклона конвертера с шестью приводными двигателями ( а ); двухмассовая расчетная схема ( б ); выражение для собственной частоты колебаний двухмассовой системы ( в ):

M i – момент, развиваемый i -м приводным электродвигателем; J i – момент инерции i -й массы;

J 7 - момент инерции венцовой шестерни; C_i7 - жесткость i -го валопровода; Аф i - зазор в i -м валопроводе

Fig. 4. Design model of the converter tilting mechanism with six drive motors ( a ); two-mass design model ( б ); expression for the two-mass system natural oscillation frequency ( в ):

M i is the moment (torque) developed by the i -th drive motor; J i is the moment of inertia (second moment) of the i -th mass; J₇ is moment of inertia of the ring gear; C_i7 is stiffness of the i -th shafting; Аф i is gap in the i -th shafting

Можно предположить, что в идеальном случае

J 1 = J 2 = … = J 6 , C 1–7 = C 2–7 = … = C 6–7 . (5)

Учитывая предыдущие соотношения, получим

6°Я. = JJ- .      (6)

( n )₂ ) ^{2    2} J 1 + J ,

Отношение собственных частот колебаний при подключении одной ветви валопровода и всех ветвей к венцовой шестерне:

^°2Ь = ^J । ⁺ J ⁷ .         (7)

( 0 12 ) ^{2   6} J 1 ⁺ J 7

Общее выражение:

^(O 12)  _ ^J 1 ⁺ J ₇ _  O’ ; _ I ^J i ^{+ J} 7

= > =            •  (8)

(Q™) ²    nJ I + J 7     ОГ ;    ^nJ I + J 7

То есть в процессе разгона собственная частота колебаний многомассовой системы (приведенной к двухмассовой) будет ступенчато изменяться в функции подключения валопроводов к ведущей шестерне (выбора зазоров в передачах). В момент окончания выбора зазора будут происходить удар и возбуждение колебаний в электромеханической системе [17, 18].

Одна из причин увеличения числа приводных двигателей механизма наклона конвертера – стремление уменьшить габаритные размеры контактных пар ведущая шестерня – венцовая шестерня и, как следствие, снизить динамические нагрузки на элементы приводных ветвей в пуско-тормозных режимах.

Очевидно, что установка приводных блоков механизма наклона конвертера требует высокой квалификации наладчиков, но даже в этом случае не удается идеально установить зацепление в контактных парах. В пуско-тормозных режимах нагрузка на валопроводы будет существенно различаться из-за различных вели-

2020;5(3):253-265

чин зазоров в контактных парах. Выше было отмечено, что наибольшая нагрузка будет на двигатель, по линии валопровода которого имеет место минимальный зазор (или он отсутствует), т.е. перегрузка по линии этой ветви будет максимальной. Время максимума нагрузки будет относительно небольшим, так как оно зависит от времени выбора минимального зазора по дру-

М     -М - Т d ®/ •

M 1дв M 17   M 8 17 = J 1   /Д; ;

M 2дв - M 27 - M 8 27 = J 2 d %;

.............................................. (11)

м бдв - M 67 - M , 67 = J 6 dy_dt ;

M 17 + M 27 + ...+ M 67 - M с = J 7 ^d ^t.

гим ветвям. В дальнейшем нагрузки по контакт-

Условия существования упругих моментов:

ным парам будут снижаться, и при установившемся характере движения будет наблюдаться их усреднение [19, 20].

В процессе выбора зазора Аф з двигатель разгоняется, допустим, при постоянном ускорении; в конце выбора зазора он достигает скорости ω 1нач , с которой и происходит удар в зацеплении. Запасенная кинетическая энергия частично рассеивается в передачах, а другая ее часть идет на создание упругих деформаций, которые вызывают дополнительные нагрузки в механической системе. Эти нагрузки могут быть оценены с помощью динамического коэффициента K дин [4, 5], который представляет собой отношение максимального упругого момента М упр.макс к базовому М баз :

^M 17 = C 12 ( Ф 1 ^- ф ? ) ; ^M 17 = 0,|Ф 1 ^- Ф 7, ^— А ф _Г7 ;

^M 17 >  0, ^{ф -} Ф 7| >^А фт

^M 27 = C 27 ^{( ф} 2 ^{- ф} 7 ) ; ^M 27 = ^{0 1 ф} 2 ^{- ф} 7 | ^{— А ф} 27 ;

' M 27 >  0,|ф 2 - ф 7| >А ф 27 ;                      ⁽¹²⁾

^M 67 = ^C 67 ( ф б ^- ф 7 ) ; ^M 67 = ⁰,¹ ф б ^- ф 7| ^{— а}ф 67 ; ,^M 67 >  ⁰,¹ ф 6 ^- ф 7| > ^А ф 67 .

Учет диссипативных сил в передачах (1 - 6):

M δ17	= b ( W 1	« 7 ) ;
M δ27	= b ( w 2	- « 7 ) ;
M δ67	= b ( « 6	- « 7 ) .

K дин

М упр.макс

/ М баз .

В качестве базового удобно принимать среднюю величину упругого момента в передаче М упр.ср . Для двухмассовой упругой системы с выбранным зазором и W 1 нач выражение для K дин примет вид

K дин

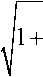
22 C 12 ω 1нач

12 упр.ср.

где С 12 - приведенная жесткость двухмассовой системы; J 1 , J г - моменты инерции первой и второй масс.

Для рассматриваемых, например, шести приводных двигателей (с одинаковыми паспортными данными) и однотипных линий связи с венцовой шестерней в общем случае можно записать уравнения движения одного и того же вида для каждой ветви [20]:

При моделировании многодвигательного электропривода механизма наклона конвертера важно учесть схемы соединения групп электродвигателей - последовательное, параллельное, смешанное. Необходимо стремиться к сокращению числа групп с последовательным или параллельным соединением двигателей, имея в виду их недостатки. Наиболее благоприятными динамическими условиями будут обладать электроприводы с индивидуальным питанием двигателей от тиристорных преобразователей, когда вопросы токоограничения будут решаться в зависимости от нагрузок по каждой из ветвей механической связи [5, 12, 21].

Демпфирующие свойства электропривода можно оценивать по величине коэффициента электромеханической связи - K эс . Для системы управляемый преобразователь - двигатель (УП - Д) при Т пр = 0 и K от = 0 величина K эс находится из выражения [5, 6, 9]

2020;5(3):253-265

^K эс

Y ^- 1

7Y ( Y - 1 ) T " + Y T Y'¹ ' ’

где у = ( J_x + J ₂) / J_x - величина относитель-

ного момента инерции.

Частота свободных колебаний вала двигателя при жесткой заделке вала механизма:

Q = Ь .            (15)

V Y - 1

Связь Ω 12 с Ω 0 через γ:

Q 12 =Q o    ^Y— .         (16)

V Y - 1

Величина K эс при различном сочетании параметров электропривода для разомкнутой системы УП – Д может изменяться в широких пределах 0 <  K эс с <  ∞. Диапазон изменения K эс предлагается рассматривать в трех интервалах, соответствующих слабой (0 <  K эс < 0,2), существенной (0,2 <  K эс < 2) и жесткой ( K эс > 5) электромеханической связи, двигатель обладает жесткой механической характеристикой. Имея конкретные значения K эс для системы, можно судить о демпфирующей способности электропривода, т.е. о взаимовлиянии электрической и механической частей ЭМС [16].

Контроль теплового состояния и виброспектров узлов механизма наклона

Приведенные выше способы оценки технического состояния ЭМС механизма наклона конвертера (по величине изменения собственной частоты колебаний системы, величине коэффициента динамичности, величине коэффициента электромеханической связи) не дают возможности оценить степень неисправности отдельных звеньев системы. Поэтому нами используется один из современных методов контроля – метод оценки теплового состояния элементов. С другой стороны, может быть получена достоверная информация о состоянии узлов ЭМС механизма наклона конвертера с помощью методов вибродиагностики.

При работе механизма наклона основную нагрузку от веса конвертера воспринимает опорный подшипник [17, 22–24]. На рис. 5, 6 показаны разрушение подшипника опорного кольца, термограмма корпуса исправного подшипника, а также спектр виброускорения поврежденного подшипника. Необходимо констатировать, что характерным признаком повреждения подшипника является рост высокочастотной вибрации в области 2–4 кГц [20, 25, 26].

Возможный характер разрушения шестерен редукторов, износа зубчатого венца показан на рис. 7, 8. Вид разрушения позволяет судить о динамическом характере нагружения и значительных силах в зацеплении [27].

а

б

Рис. 5. Опорный подшипник конвертера:

а – разрушение опорного кольца; б – термограмма корпуса

Fig. 5. Converter backing bearing:

a – failure of the support rim; b – shell thermogram

2020;5(3):253-265

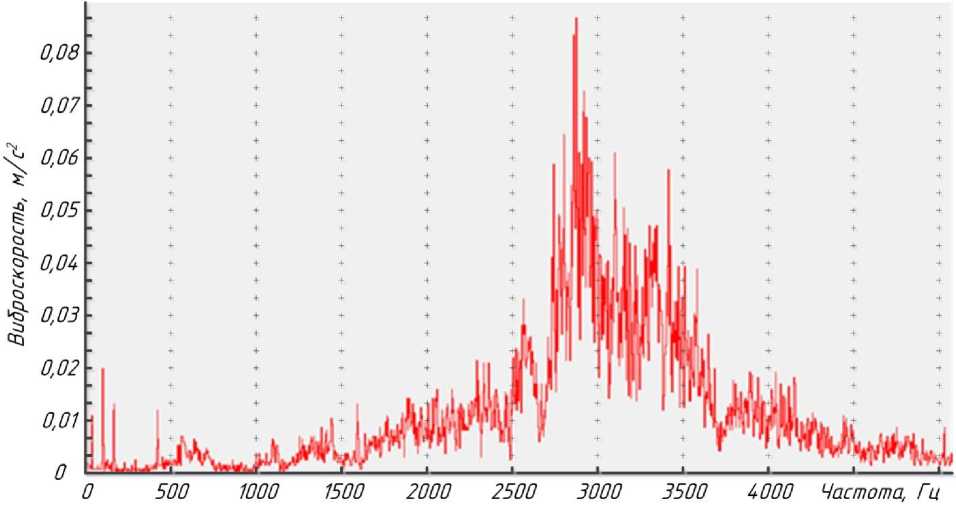
Рис. 6. Спектр виброускорения поврежденного подшипника

Fig. 6. Vibration acceleration spectrum of damaged bearing

Рис. 8. Повреждения зубчатого венца

Fig. 8. Damage to gear rim

Рис. 7. Разрушение шестерен редукторов

Fig. 7. Failure of reduction pinions

Результаты исследования динамики привода наклона конвертера на основе математического моделирования

Для одного из типовых механизмов наклона конвертера с многодвигательным электроприводом с помощью программного пакета Matlab выполнено моделирование пускового режима с вариациями значений приведенного зазора при условии одинаковых жесткостей валопроводов. Рассмотрены одновременные пуски двух приводных двигателей при условии, что Δϕ 1 = Δϕ 2 и С 12 = С 22 (рис. 9–12).

Момент сил сопротивления на этапе разгона задавался ступенчатой зависимостью от M c0 до M c ном . В качестве системы электропривода рассматривалась система тиристорный преобразователь – двигатель постоянного тока с независимым возбуждением (металлургического исполнения). Для удобства оценивания результатов моделирование было выполнено в относительных единицах. На приводимых осциллограммах моментов и частот вращения расчетных масс хорошо прослеживается удар при выборе зазоров, значения упругих моментов достигают

2020;5(3):253-265

практически трехкратного номинального значения ( M н ). Колебания упругих моментов затухают за относительно короткий промежуток времени. В рамках этого интервала времени происходит затухание частот вращения расчетных масс. По окончании выбора зазоров имеют место удар и частичное снижение частоты вращения приводных двигателей.

Здесь и на рис. 11: M 1 , M 2 – моменты,

M 12 , M 23 , M 42 – упругие моменты в валопроводах между электродвигателями, венцовой шестерней и конвертером.

Здесь и на рис. 12: ω 1 , ω 4 – частоты вращения электродвигателей приводов; ω 2 – частота вращения венцовой шестерни, ω 3 – частота вращения конвертера.

развиваемые электродвигателями приводов;

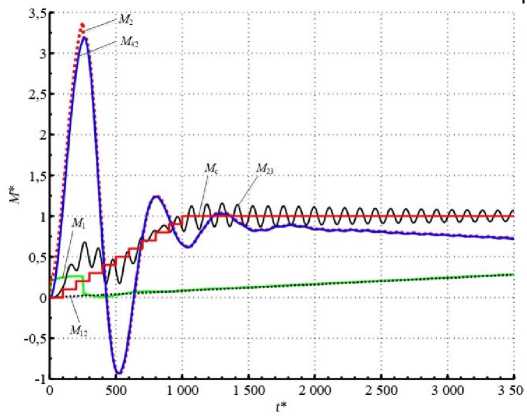
9. Графики моментов при пуске разветвленной

Рис многомассовой модели ЭМС механизма наклона кон-

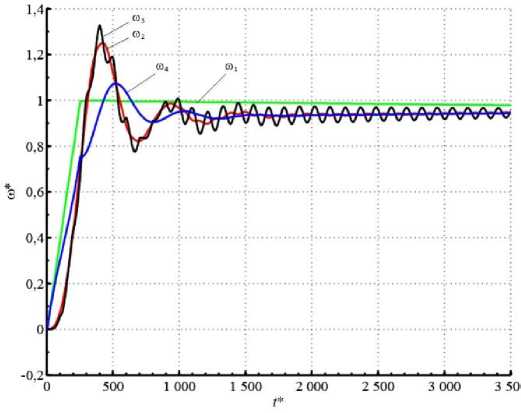
Рис. 10. Графики скоростей при пуске разветвленной многомассовой модели ЭМС механизма наклона кон-

вертера при равных зазорах в ветвях

вертера при равных зазорах в ветвях

• Fig. 9.    Graphs of momenta at starting branched multimass model of the converter tilting mechanism EMS at equal gear backlashes in the branches

• Fig. 10.    Graphs of speeds at starting branched multimass model of the converter tilting mechanism EMS at equal gear backlashes in the branches

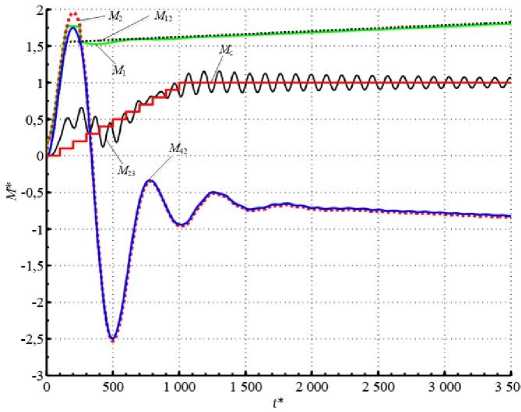
Рис. 11. Графики моментов при пуске разветвленной многомассовой модели ЭМС механизма наклона конвертера при разных зазорах в ветвях

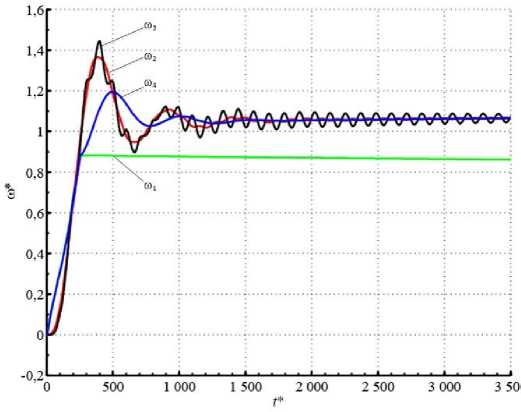
Рис. 12. Графики скоростей при пуске разветвленной многомассовой модели ЭМС механизма наклона конвертера при разных зазорах в ветвях

Fig. 11. Graphs of momenta at starting branched multimass model of the converter tilting mechanism EMS at different gear backlashes in the branches

Fig. 12. Graphs of speeds at starting branched multimass model of the converter tilting mechanism EMS at different gear backlashes in the branches

I ГОРНЫЕ НАУКИ

I Ж И ТЕХНОЛОГИИ

2020;5(3):253-265

МИСиС

Национальный исследовательский технологический университет

В случае когда Δϕ 1 <  Δϕ 2 , практически всю нагрузку принимает первый двигатель – в момент удара запасенная кинетическая энергия трансформируется в упругий момент в первом валопроводе, упругий момент достигает четырехкратного номинального значения. Подключение второго двигателя приводит к росту частоты вращения первого (после просадки скорости в результате удара), а также наблюдается переход всей электромеханической системы в режим затухания колебаний, который продолжается в течение нескольких секунд.

Выводы

1. Перегрузки в механических передачах многодвигательного электропривода механизма наклона конвертера приводят к выходу из строя подшипниковых узлов и шестеренных пар. Перегрузки возникают вследствие неточности изготовления механических кон-

тактных пар, а также отклонений при проведении монтажных операций по установке приводных групп.

• 2.    Неодновременность выбора зазоров по линии каждого из валопроводов приводит к перераспределению нагрузок между приводными электродвигателями, большие нагрузки принимают на себя линии передач с меньшими приведенными зазорами.

• 3.    Существенно снизить нагрузки в передачах возможно за счет применения двухступенчатого задатчика интенсивности U зи ( t ), когда на начальном этапе разгона выбор зазоров происходит при малой частоте вращения, после их выбора темп U зи ( t ) возрастает до допустимого значения по условиям ограничения ускорения.

• 4.    Непосредственная информация о текущем техническом состоянии элементов объекта может быть получена с помощью термои вибродиагностики.

2020;5(3):253-265

2020;5(3):253-265