Вопросы использования БПЛА для проведения мониторинга качества береговых вод

DOI:

Хорошо известно, что беспилотные летательные аппараты (БПЛА) обладают высоким пространственным разрешением и не имеют такие проблемы, свойственные спутниковому дистанционному зондированию как влияние атмосферы, облаков [2]. БПЛА широко используются для определения качества береговых вод [3; 4; 7; 10].

Исследования качества береговых вод проводятся путем проведения с помощью как морских измерительных станций, так и БПЛА, оснащенных мультиспектральной и гиперспектральной аппаратурой. Например, как указывается в работе [11], с этой целью были использованы восемь станций, установлены в заливе Chesapeake (США). Станции были оснащены гиперспектральными измерителями, работающими в спектральном диапазоне 320–950 нм с интервалом 3,3 нм. Полученные результаты сопоставлялись с результатами измерений с применением БПЛА, оснащенными пятиканальными измерителями Mica Sense. Это устройство имеет следующие измерительные каналы: синий канал (475 нм, ширина полосы 32 нм); зеленой канал (560 нм, ширина полосы 27 нм); красный канал (668 нм, полоса пропускания 14 нм); канал края красной зоны (717 нм, полоса пропускания 12 нм); канал NIR (842 нм, с полосой 57 нм).

В указанных морских станциях проводятся контактные измерения хлорофилла и общего количества взвешенных частиц (TSS).

Вместе с тем, применительно к береговым зонам элементами загрязнения морских вод считаются водоросли, или морская капуста (kelp), которая является трехморным высокопродуктивным морским растением, представляющим экономическую ценность для населения прибрежной зоны [6; 8]. Указанный фактор актуализирует исследование к оценки потенциала этого растения как его надводной, так и подводной компоненты. Учет объема надводной части с использованием ее излучения в NIR области затрудняется наличием морским блеском в поверхности воды, мутностью воды [1; 9].

Традиционным образом, учет и исследование состояния растений осуществляется применением сигналов спектральной зоны «край красной зоны» (670–750 нм).

В общем случае, суммарный сигнал NIR диапазона, регистрируемый спектрометрами БПЛА определяется как

R uas ( NIR ) = R rs ( NIR ) + p ( NIR ) + '₁ ,   (1)

Ed где RRS(NIR) – сигнал NIR диапазона, извлекаемая с поверхностной части растительности; ρ(NIR) – компонента NIR диапазона из-за блеска поверхности воды; Lsky – небесное излучение; Ed – пере излучения из глубин воды.

Маскирование ρ ( NIR ) согласно [11] может быть осуществлено методом «темного»

Lsky пикселя, а компонента определяется с ис-Ed пользованием модели радиационного переноса [6]. Компоненты Rrs(NIR), может быть оп- ределена с помощью нелинейного регрессионного уравнения [5].

С учетом (3) и (4) напишем

R rs ( NIR ) = 0,025exp

- 3,469 - R uas ( blue ) . Ruas ( red edge ) .

+ 0,00013. (2)

R r2s ( NIR ) = 0,025 U_rs ( NIR ) exp

- 3,469 - R uas ( blue ) R UAS ( red edge X R rs ( NIR ) )

+ 0,00013 R rs ( NIR ).

+

Регрессионная функция (2) графически изображена на рисунке. Таким образом, задача обеспечения уменьшения доли сигнала R_UAS ( NIR ) в сигнале R_UAS ( red edge ) сводится к уменьшению влияния R_rs ( NIR ). При этом следует определить такую взаимосвязь между и при которой такое влияние могло бы быть приведено к минимуму.

Материалы и методы

Для решения указанной задачи можно ввести на рассмотрение функциональную зависимость

R UAS ⁽ red edge) = R UAS ⁽ red ^edg^{e) (} R rs ( ^NIR )) ⁽³⁾

Рассмотрим сценарий, когда БПЛА исследует множество точек в зоне береговых вод в количестве n . Из полученных результатов измерений можно сформировать два множества:

Rrs(NIR) = {Rrs(NIR)}; i = 1,n ;(6)

RUAS (red edge) = {RUAS (red edge)} }; J = 1, n .

Будем считать, что множество R_rs ( NIR ) является упорядоченным, то есть элементы удовлетворяют условию

Rrs (NIR) = Rrs (NIR),-, + ARrs (NIR), где 'ARrs (NIR) = const; Rrs (NIR)0 = 0.

И далее вычислить такой вид функции (3), при которой некоторый функционал, характеризующий мощность сигнала R_rs ( NIR ) достиг бы минимума.

Рассмотрим возможность формирования функционала, характеризующего мощностные характеристики R_rs ( NIR ) по множеству исследуемых береговых зон, загрязненных водорослью типа «морская капуста». Умножим каждую из сторон выражения (2) на R_rs ( NIR ). Получим

С учетом (5) и (8) составим дискретную сумму F_g , где

F g = E n = i 0,025 U rs ( NIR ), exp

3,469 - R _uas ( blue )

^RUAS ⁽ red edge ^{) ( R}rs ^{( NIR} )).

R s ( NIR ) = 0,025 R_rs ( NIR ) exp

- 3,469 - R uas ( blue ) . Ruas ( red edge )

+ 0,00013 R_rs ( NIR ).

Рассмотрим задачу выбора такого вида функции R _uas ( red edge ) ( R_rs ( NIR )) , при которой F_g достигает минимума, то есть суммарный вклад отраженной ближне-инфракрасной радиации от надводной части морского растения достигает минимума и в основном извлекается R_UAS ( red edge ), то есть извлекается информация о подводных частях этого растения.

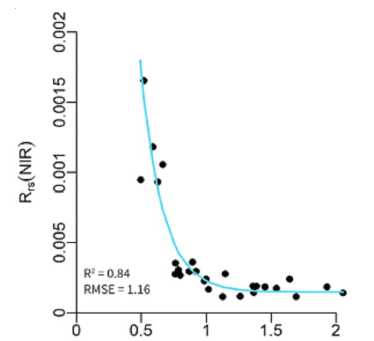
RuAs(blue)/RUAS(rededge)

Кривая нелинейной регрессионной функции взаимосвязи между отношением

^R UAS ( ^blue ) R uas ( red edge )

и R_rs ( NIR )

Для решения указанной задачи в первом приближении осуществим переход от дискретной модели (9) на непрерывную модель в виде непрерывного функционала F_H , где

F H = j O' rs ⁽ NIR ) 'ax 0,025U_rs ( NIR ) exp

3,469 • R _uas ( blue ) R uas ( red edge )( R rs ( NIR )).

X d ( Urs ( NIR )).

X

Решение непрерывной оптимизационной задачи (10) может быть осуществлено по методу вариационного анализа при выполнении одного условия, суть которого заключается в наложении к искомой функции определенного ограничительного условия. Рассмотрим случай, когда указанное ограничительное условие F _огр имеет вид

F orp = f U rs ( ^NIR) ""R uas ( red edge 1 x x ( R_rs ( NIR )) d ( R rs ( NIR )) = C , где C = const .

Из (15) находим

J      ^3,469 • R UAS ( blue ¹     =

[ R UAS ⁽ red edge X ^Rrs ^{( NIR ))}.

^R uAA rededge^

0.025U _rs ( NIR 1 3,469 • R _uas ( blue 1 '

Таким образом, полученное выражение (16) является трансцендентным уравнением относительно искомой функции R _uas ( red edge ) ( R_rs ( NIR ^ Задача нахождения оптимального вида этой функции не имеет аналитического решения и может быть решена вычислительным путем при заданных значениях R_rs ( NIR ) и R_UAS ( blue ).

Решение задачи удовлетворит условие достижения минимума функционала (10), так как вторая производная интегранта в функционале (14) по искомой функции оказывается положительной величиной.

Заключение

Отметим, что смысл ограничения (11) заключается в сужении пространства непрерывных и дважды дифференцируемых функций до некоторого подпространства, элементы которого удовлетворяют условию (11). С учетом (10) и (11) составим целевой функционал F ₀ безусловной вариационной оптимизации по следующей схеме:

F o = F h + ^ [ F _Or_P — C ]■             (12)

С учетом (10), (11), (12) получим

F 0 = j 0 ^{rs ( NI}R ¹ "ax 0,025 U_rs ( NIR ) exp

3,469 • R _uas ( blue ) R UAS ⁽ red edge X R rs ^{( niR} ))

X

X d ( Urs ( NIR )) +                       (13)

+ 4 U^{rs ( NI}R ¹ -Ruas ( red edge X R rs ( NIR )) d ( R rs ( NIR )) - C ] .

Решение оптимизационной задачи (13) должно удовлетворить условию:

d j o,O25 U „ ( NIR )exp [-

^3,469 • R UAS ^{( blu}e )     1

R A ⁽ red edge X R s ^{( NI}R 1Ц

- ^ ^R UAS ⁽ red edge X ^R„ ^{( NIR 11}

^dR UAS ⁽ red edge X ^R„ ^{( NIR 11}

= o. (14)

С учетом (14) получим

0,025 U_rs ( NIR 1 exp

3,469 • R _uas ( blue 1

Ruas (red edge1(Rrs (niR 11.

_X      ^3,469 • R UAS ^{( blue 1}      - _л = 0

R UAS ⁽ red edge ^{1( R} rs ^{( NIR 11 2}

Сформулирована и решена задача оптимального использования БПЛА для мониторинга качества береговых вид. Отмечена, что качество береговых зон определяется в основном количеством водорослей и в частности морской капусты в береговых водах. При этом основная масса этой растительности оказывается под водой. Надводная часть обычно оценивается с большой погрешностью методами дистанционного зондирования так как требуется учесть влияния блеска и мутности морской поверхности. Таким образом, учет подводной части водорослей должен быть осуществлен путем такой оценки R_UAS ( red edge ), которая в минимальной степени подвержена влиянию R_rs ( NIR ). Для этой цели использована известная регрессионная зависимость R_rs ( NIR ) от отношения R_UAS ( blue )/ R_UAS ( red edge ). Введена на рассмотрение функция R_UAS ( red edge ) ( R_rs ( NIR )) и сформирована задача поиска такого вида этой функции, при которой целевой функционал, формированный на базе указанной регрессионной зависимости и некоторого ограничительного условия наложенного на искомую функцию, достиг бы минимума. Получено трансцендентное уравнение, решение которого позволяет определить характер искомой зависимости.