Вопросы кинематики ходовой системы бесчокерной трелевочной машины на базе гусеничного трактора

Динамические нагрузки на технологическое оборудование в продольно-вертикальной плоскости возникают при наезде машины на препятствие одновременно двумя бортами. При этом факторами, оказывающими значительное влияние на нагруженность элементов конструкции, являются высота препятствия и скорость движения машины [3]. Для исследования влияния данных факторов на нагруженность элементов конструкции технологического оборудования машины необходимо выполнить анализ кинематики движения и разработать математическую модель системы «трелевочная машина + груз». Исходя из этого, целью настоящего исследования является анализ влияния кинематических параметров трелевочной машины на траекторию движения точки, расположенной на конце стрелы, при переезде через препятствие.

Результаты исследований и их обсуждение. На рисунке 1 показана расчетная схема переезда трелевочной машины на базе гусеничного трактора ТЛТ-100 через препятствия одновременно двумя катками задней каретки трактора. Для упрощения расчетной схемы представим данную систему в виде треугольника ABC. При этом точка A перемещается поступательно по направлению движения машины, точки B и C одновременно совершают переносное поступательное движение и вращательное движение относительно точки A [5]. Для определения положения точки B получена следующая зависимость:

h_B (t) = l₃ • sin [c + sin^-1 (^p^] — l₃ • sin o' ,                               (1)

где    hB (t) - текущая высота точки B относительно положения при движении по горизонтальной поверх ности, м;

• l₃    - расстояние от точки A до точки B, м;

• 11    - расстояние от точки A до точки C, м;

• о - угол BAC, град;

h_c (t) - текущее перемещение точки C относительно положения при движении по горизонтальной поверхности, м.

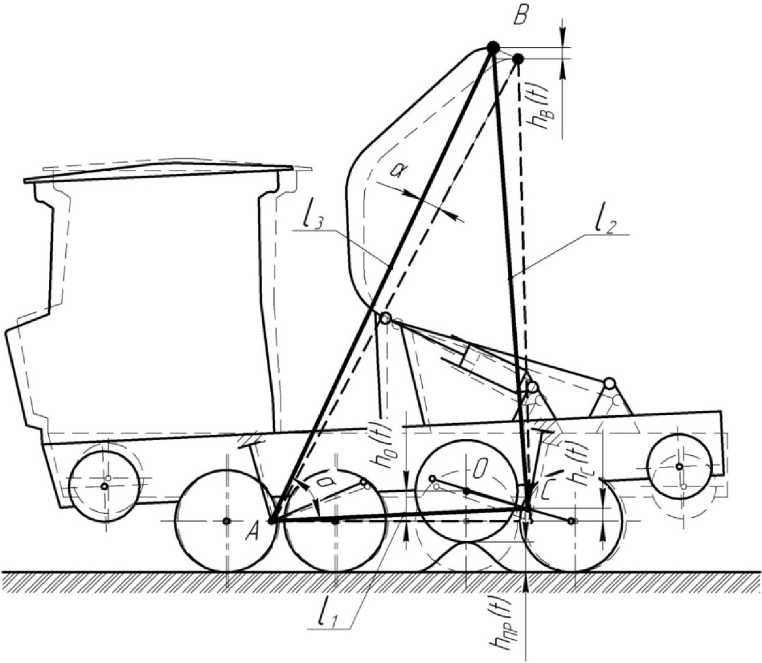
Рис. 1. Расчетная схема перемещения трелевочной машины через препятствия двумя бортами

Условимся, что при переезде катка через препятствие, имеющее косинусоидальный профиль [2], ось вращения катка (точка O) движется по дуге окружности (рис. 2).

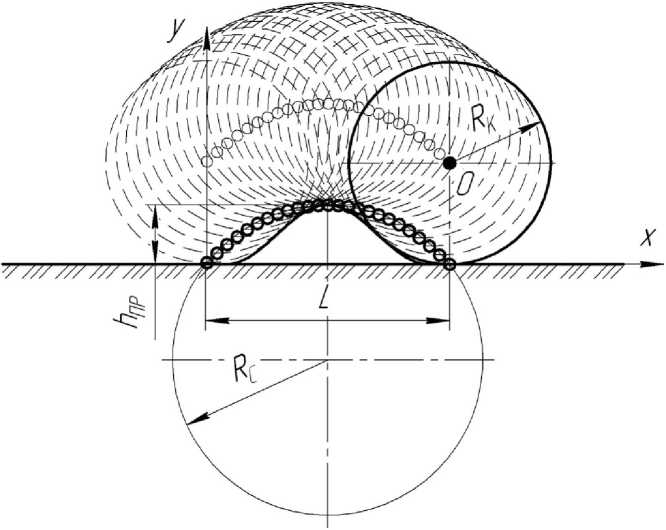
Рис. 2. Траектория движения оси вращения катка при переезде через препятствие

Исходя из этого, используя уравнение окружности, получаем зависимость положения точки O от высоты препятствия hПР h0 (t) = Уо + ^Rq - (x- %o)2,(2)

где у0 - начальная координата точки O по оси у, м уо = hпр - Ro, где h ПР - максимальная высота препятствия, м;

R_o - радиус траектории точки O, м

Ro = Rk + h пр ;(4)

x - координата точки O по оси х, м; x = L(t) ;

x₀ - начальная координата точки O по оси х, м;

хо = ^О-У0.

На рисунке 3 видно, что точка O располагается несколько выше, чем точка C; исходя из правила подобия треугольников [6], получим следующее соотношение hс(t) = ho (t) -^

“ 2

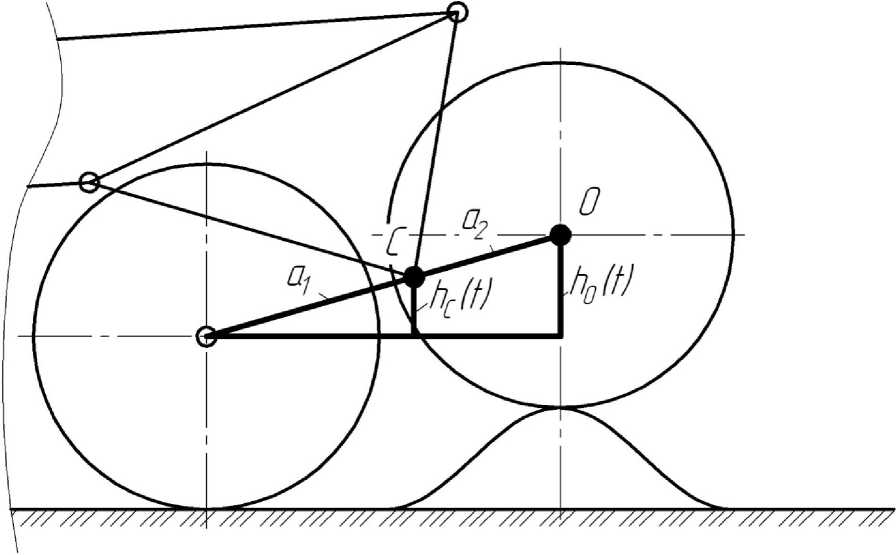
Рис. 3. Схема переезда катка через препятствие

Подставив в формулу (1) выражения (2) и (3), получим траекторию движения точки B hB(t) = l3 • sin

a + sin ¹

|уо+^?1Д^7|^

—

l3

• sin a .

Используя формулу (7), выполним расчёт по ряду точек (рис. 4): a 1 , a 2 , a 3 , b 1 , b 2 , b 3 , c 1 , c 2 , c 3 . Для каждой точки построим траекторию движения (рис. 5).

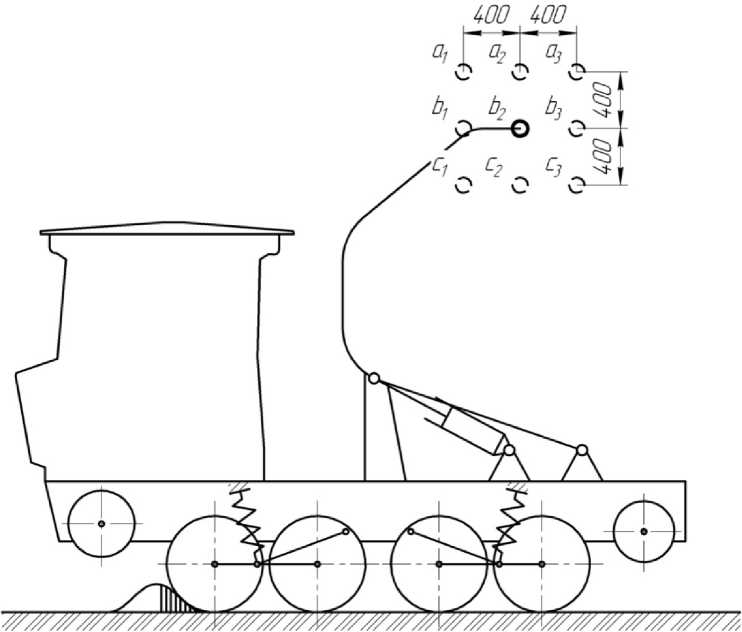
Рис. 4. Схема расположения исследуемых точек

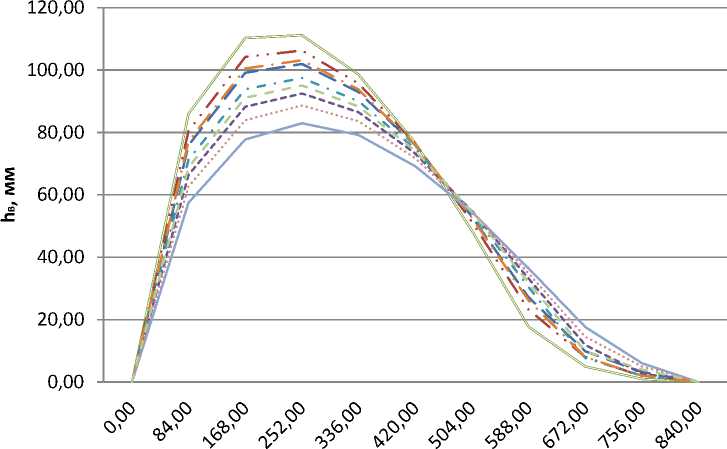
L, мм

Рис. 5. График траекторий движения исследуемых точек

a1

a2

a3

b1

b2

b3

c1

c2

c3

На рисунке 6 показана зависимость максимальных значений h B от звена l 3 .

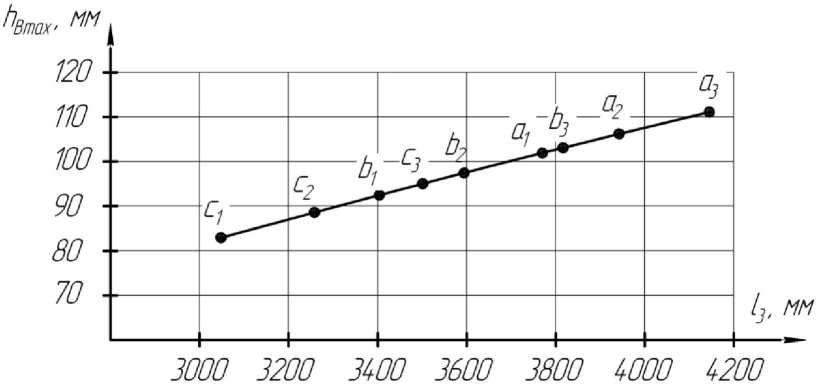
Рис. 6. Зависимость максимальных значений h B от звена l 3

Заключение. При переезде трелевщика через препятствие величина максимального отклонения точки крепления захватного устройства к стреле (точки B) имеет пропорциональную зависимость от звена l 3 . Коэффициент пропорциональности в данном случае будет равен 0,027. Отсюда следует, что при уменьшении радиуса поворота точки B относительно оси вращения трелевочной машины (звена l 3 ) уменьшается величина h B , которая влечет за собой снижение динамических нагрузок на технологическом оборудовании.