Вопросы математического моделирования радиоинформационных систем

ВЕСТНИК 2016

Математическое моделирование явлений, процессов и конструкций сложных технических систем, каковыми являются радиоинформаци-онные системы (далее РИС), является мощным инструментом теоретического анализа задач, возникающих в различных областях естествознания. Имитация на ЭВМ функционирования сложных (проектируемых или реально существующих) систем – практически единственный способ быстрого решения актуальных проблем науки и техники.

В последнее время в научных исследованиях интенсивно развивается новый подход к исследованию сложных явлений с позиций вычислительного эксперимента [1]. Этот подход играет важную роль и при разработке систем автоматизации проектирования радиоинформационных систем, поскольку он позволяет вместо имитации РИС путем ее макетирования разрабатывать такие вычислительные алгоритмы, которые позволяют моделировать функционирование РИС и исследовать их свойства математическими методами.

Отметим, что в настоящее время машинный анализ является, например, обязательным элементом при проектировании сложных электрон- ных схем. Как известно, анализ РИС есть первый шаг к их проектированию. Автоматизированное проектирование РИС является предметом широких исследований многих коллективов и требует хорошего понимания проблем, возникающих при разработке технологического цикла вычислительного эксперимента.

Как и в любой инженерной задаче, конструирование модели РИС состоит из нескольких основных этапов. При конструировании модели целесообразно выделять следующие основные этапы.

• 1    этап . Он состоит в построении качественной, например физической, модели изучаемой проблемы, т.е. в задании некоторых представлений о моделируемом объекте в том или ином естественно-научном языке.

Функциональное описание и анализ моделируемого объекта, очевидно, являются первоосновой для построения качественной математической модели. Этот этап наиболее ответственен и определяет стратегию решения задачи. От того, насколько всесторонне и квалифицированно опущены несущественные факторы, выявлены основные факторы и установлены закономерности, которым они подчиняются, и на этой основе создана последовательность систематически усложняемых (и уточняемых) функциональных схем объекта, во многом зависит успех использования будущих математических моделей и принятие соответствующих решений.

Как известно, выработка соответствующих рекомендаций обычно относится к компетенции конструкторов и не входит в обязанности специалистов по математическому моделированию. Однако после того как соответствующая структура (или последовательность структур) выбрана, можно переходить ко второй, чисто математической, части задачи – построению класса математических моделей.

• 2    этап. Построение математических моделей для измерительных систем на общем уровне – это построение некоторого оператора, отображающего множество входных данных X во множество результатов Y.

Сразу же отметим, что собственно этапу построения математической модели (построению оператора А) , как правило, предшествуют следующие два действия:

• 1 ) выбор уровня детализации для моделирования;

• 2 ) выбор математического описания.

При этом, поскольку оператор А не обязательно должен давать самое подробное описание системы (хотя, вообще говоря, естественно стремиться ко все более подробному описанию системы (модели)), выбор уровня детализации ее диктуется следующими двумя требованиями: во-первых, описание должно быть достаточно подробным, во-вторых, оно должно быть достаточно простым. Таким образом, здесь приходится идти на компромисс между точностью моделирования, с одной стороны, и простотой модели, с другой. Если этот компромисс найден, то основной задачей тогда является определение оператора А .

Что же касается вопроса выбора математического описания, то здесь основная проблема с точки зрения автоматизации проектирования измерительных систем – это разработка удобно-

Объект

Физическая модель

Сателлит №1 в.э.

Поставляет коэффициенты

ЛМатематическая модель

• 1.    Выбор уровня детализации

• 2.    Выбор математического описания

• 3.    Построение математической модели

• 4.    Проверка корректности построения

Уточнение математической модели

ВЕСТНИК 2016

Численные методы

Дискретная модель

• 1.    Разработка алгоритма

• 2.    Исследование алгоритма

• 3.    Реализация алгоритма

Программа

Уточнение дискретной модели

• 1.    Отладка

• 2.    Тестирование

• 3.    Верификация

Расчеты

• 1.    Планирование

• 2.    Проведение

• 3.    Отработка

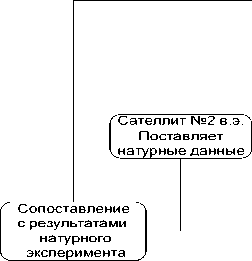
Рис. 1. Основные этапы технологического цикла вычислительного эксперимента

ВЕСТНИК 2016

го для конструктора языка, с помощью которого можно описывать как саму систему, так и множество вариантов будущей системы.

Анализ внутреннего строения различных моделей для измерительных систем показывает, что наряду с определенной спецификой они имеют и много общего. А именно, любая сложная модель строится на основе сравнительно более простых с помощью определенных композиций.

С нашей точки зрения, это фундаментальный факт в изучении внутренней структуры логикофункциональной природы, или сущности, моделей и моделирования в целом. Поэтому адекватное выделение и исследование на различных уровнях композиций моделей представляет собой центральную проблему моделирования.

Иными словами, модели – это не просто любые операторы, а такие, которые имеют определенную структуру. Структура этих операторов характеризуется тем, что компонентами ее являются операторы (как правило, более простые, чем исходные) и предикаты (распознаватели).

Во множестве компонент такого типа выделяются операторы входа и выхода. Из указанных компонент путем подключения выходов операторов к входам строится модель.

Понимание математических моделей для РИС в таких терминах позволяет установить определенные соответствия между моделью и программой и, следовательно, использовать методы теории программирования для изучения математических моделей данного класса. Однако при этом возникают и определенные трудности: во-первых, при моделировании сложных РИС возможны ситуации, когда некоторые объекты (или отдельные элементы) имеют несколько входов и выходов с одновременным поступлением информации по ним, что не допускается в стандартных программах; во-вторых, в качестве базисных элементов в моделях могут использоваться конкретные физические объекты (например, интегратор, реактивная лампа, временной дискриминатор и т.д.), которые трудно выразить композициями базисных средств языков программирования. Уже к первой ситуации приводит, например, наличие положительных и (или) отрицательных обратных связей, т.е. замкнутых циклических путей в функциональной схеме моделируемого объекта.

Вместе с тем при таком подходе существует целый ряд положительных моментов: во-первых, мы в модели сохраняем структуру объекта, что удобно, например, при поиске и локализации ошибок на уровне наших представлений, во- вторых, построенная по таким принципам модель (схема модели) удобна при ее реализации на ЭВМ.

В заключение отметим, что второй этап включает также построение некоторой целевой функции, по которой в дальнейшем будет оцениваться корректность математической модели.

• 3    этап. В содержательном плане этот этап может представляться в виде нескольких шагов. Начальная стадия его заключается в исследовании математических задач, возникающих в связи с построением математической модели. Основным на этом этапе является решение прямой задачи, т.е. получение теоретических следствий из принятой модели. Задачи, решаемые на этом этапе, являются типично математическими, и для их решения может применяться как развитый аппарат классической математики, так и имитационное моделирование с помощью ЭВМ. При этом сначала может использоваться достаточно грубая модель. В случае необходимости можно производить уточнение модели. Переход к более точной модели, вообще говоря, должен производиться согласованно с более грубым описанием. Таким образом, исследователь может иметь дело с целой системой «вложенных» друг в друга моделей.

Как отмечалось выше, основная цель, которая ставится при построении математических моделей, – это получение простого способа нахождения качественных и количественных характеристик отдельных сторон функционирования реальной (проектируемой) физической системы [3]. Семейство моделей реализует эту цель только в том случае, если в этом семействе существует такая модель (такие модели), на которой достигается совпадение (в определенном смысле) заданных характеристик системы и модели, т.е. когда положительно решен вопрос об адекватности математической модели заданным физическим представлениям. Рассмотренные эмпирические соображения допускают математическую формализацию, которая, с нашей точки зрения, позволяет достаточно эффективно реализовать процесс построения математических моделей сложных измерительных систем [4].

Как известно, математическая модель задает характер поведения для неопределенного, часто даже бесконечного числа возможных процессов. Такие процессы различаются значениями переменных в соответствующих интервалах времени и, в частности, начальными значениями. Возникает вопрос, каким образом убедиться, что в любом из процессов, которые можно выполнить в соответствии с данной моделью, получаются правильные результаты? Этот вопрос правильности математических моделей является одним из основных, решающих и неизбежных вопросов моделирования.

Одним из методов контроля точности (адекватности) математического моделирования является, как известно, метод сравнения основных показателей, найденных с помощью модели, с соответствующими показателями, полученными экспериментальным путем и отражающими все известные свойства системы [5]. Такой метод проверки правильности моделей называется тестированием. Несмотря на повсеместное использование этого традиционного способа проверки математических моделей, он обладает рядом серьезных недостатков. Во-первых, он дорог, обременителен и связан с большими затратами времени. Во-вторых, поскольку физический эксперимент часто оказывается «грязным» или затруднительным по техническим причинам, а в случае моделирования гипотетических, например проектируемых, систем вообще невозможен, то он непригоден, и необходимо разработать методы косвенного контроля точности моделирования.

Очевидно также, что экспериментальное тестирование моделей может использоваться только для доказательства наличия ошибок, но никак не для доказательства их отсутствия в исследуемой модели. Следовательно, для моделирования необходимо разрабатывать также аналитические методы проверки правильности математических моделей, доказывающие логическую правильность модели относительно выбранных условий. Таким образом, третий этап включает также и верификацию математической модели заданному физическому описанию. Последняя задача достаточно трудная, однако решение ее является очень важным, поскольку она помогает выявить имеющиеся ошибки, избегая метод тестирования. Резюмируя сказанное, отметим, что третий этап включает, вообще говоря, как построение последовательности усложняющихся и уточняющихся (в определенном смысле) математических моделей, так и верификацию каждой из них заданным физическим представлениям, поскольку последнее позволяет в конечном итоге в ряде случаев локализовать фронт работ по определению ошибок только на физическом уровне [2].

• 4    этап. На этом этапе, пользуясь математическим аппаратом, находят точные или приближенные решения соответствующих математических задач. А поскольку практические задачи матема

тического моделирования для РИС, как правило, требуют большого объема вычислительных работ, то весь процесс проходит при участии современных ЭВМ, что требует создания программ (специализированных пакетов программ), реализующих те или иные алгоритмы.

Здесь возможны два случая.

Случай 1. Если результаты расчетов неудовлетворительны (обычная ситуация на начальной стадии программирования), то переходят ко второму циклу процесса: проверяют правильность программ методом тестирования, проверки или верификации программ.

Случай 2. Если результаты расчетов удовлетворительны, то таблицы вычислений, полученные на этом этапе, сопоставляют с соответствующими экспериментальными данными (если такие, конечно, имеются) с целью выявления степени адекватности математической модели реальному объекту.

Отметим, что всё многообразие параметров математической модели и реального объекта можно условно разделить на два вида:

• 1)    количественные, например величины угла, значение ошибки, время и т.п.;

• 2)    качественные, например характер ошибки (грубая, нормальная, меньше нормы), характер режима функционирования (есть срыв, нет срыва) и т.п.

В результате статистического сопоставления данных на выходе математической модели и реального объекта можно сделать научно обоснованные выводы с заданным уровнем значимости риска о степени адекватности математической модели реальному объекту по каждому из параметров, интересующих исследователя.

• 5    этап. На этом этапе решаются следующие вопросы:

• 1)    существуют ли в принятом классе гипотетических моделей такие модели (сопоставимые), что уклонение теоретических следствий модели от данных эксперимента не выходит за пределы точности наблюдений;

• 2)    если такие модели существуют, то разрабатываются методы отбора из множества сопоставимых моделей наиболее целесообразной модели, т.е. дается интерпретация результатов наблюдений (решается обратная задача).

Здесь также возможны два случая.

Случай 1. Если результаты сопоставления удовлетворительны, то модель принимается и проводится необходимый численный эксперимент как с целью изучения отдельных сторон функционирования моделируемой системы, так и с целью активного влияния с помощью моде-

ВЕСТНИК 2016

ВЕСТНИК 2016

ли на сокращение процесса испытаний сложных систем.

Случай 2. Если результаты сопоставления неудовлетворительны, то переходят ко второму циклу процесса (рис. 1) – проводят идентификацию математической модели и снова производят сопоставление (5 этап).

Если результаты сопоставления и в этом случае неудовлетворительны, то необходимо уточнить постановку задачи на уровне физических представлений (1 этап), построить новую математическую модель (2 этап), решить соответствующие математические задачи и т.д. в соответствии с алгоритмом рис. 1.

Обратим внимание на процедуру взаимодействия между этапами «внешнего» и «внутреннего» проектирования через этап формирования облика в случае проектирования достаточно сложной системы.

Он выглядит примерно следующим образом.

• 1.    С этапа «внешнего» проектирования в конструкторское бюро поступает набор частных критериев u = { u 1 ,u 2 ,,„_mu_m } , которые условно назовем концепцией проектируемого объекта.

• 2.    В конструкторском бюро инженер вместе с математиком формируют множество X – описание возможных вариантов будущей конструкции.

• 3.    По совокупности частных критериев { u 1 ,u 2,..., u_m } формируется множество эффективных вариантов конструкции, которое поступает к представителям «внешнего» проектирования.

• 4.    Представители «внешнего» проектирования на имеющихся у них имитационных моделях функционирования объекта с использованием экспертиз и прочих процедур, требующихся для этого этапа, решают задачу

• 5.    Если решение этой задачи дает удовлетворительный результат (или несколько результатов), то он служит (они служат) для окончательного формирования технического задания представителями «внутреннего» проектирования.

• 6.    Если же решение задачи оказывается неудовлетворительным, необходимо перейти на иной уровень детализации и повторить ряд этапов. Либо – пересмотреть концепцию u = { u 1 ,u 2 ,...,u_m } и выбрать другую, например

• 7.    Если же и эта процедура к успеху не приведет, то нужно снижать требования или изобретать принципиально новую конструкцию, т.е. формировать другое множество X .

x 0 e A rgmax x _e n ₍ u , x ) F ⁽ x ) . (1)

U = { U , ... , U m } •

После чего повторяется процедура формирования, и так до тех пор, пока не определится концепция u , такая, что среди эффективных вариантов, соответствующих u , найдется удовлетворительное решение задачи.