Вопросы применения разновысотных баллонных источников оптической радиации для калибровки наземных микротелескопов сети отслеживания орбитальных спутников

Такие глобальные астрономические события, как расширение вселенной и эффект смещения красной зоны в спектре, а также необходимость отслеживания функционирующих спутников на орбите диктуют необходимость проведения периодической калибровки самих телескопов [1-2].

В качестве примера можно указать сеть наземных микротелескопов OSCOM, предназначенную для оптического слежения спутников CubeSat,

в частности для контроля высоты полета и положения солнечных панелей и антенн спутников. В системе OSCOM используются микротелескопы Celestron 14 Edge HD. Наличие информации об абсолютной яркости свечения необходимо для определения альбедо поверхности спутника. Для калибровки в данном случае используется свет звезд с известной магнитудой.

Как отмечается в [1], проведение калиброванных фотометрических измерений всегда связано с проблемой динамичности атмосферных условий, что обычно приводит к несовпадению фотометрических данных, полученных при различных временных показателях. Здесь также следует учесть такие факторы, как неточность калибровки фотометров, различные характеристики используемых оптических фильтров, использование различных калибровочных источников и т. д. [3-5].

Аналогичные проблемы существуют в наземной сети микротелескопов, используемой для наблюдения за спутниками CALIPSO [6]. Как отмечено в работе [7], неточная калибровка фотометрических устройств, совместное воздействие затуханий сигнала в видимом и близком ИК диапазонах, вносимых атмосферой и самой измерительной аппаратурой, - являются источником большой неопределенности результатов исследования свойств и величины «темной энергии». Очевидно, что повышение точности калибровки фотометрических измерителей диктует необходимость наличия специальных внешних источников оптической радиации, специально установленных на ракетах или баллонах. Использование в целях калибровки отраженной от спутников солнечной радиации или переотраженной от поверхности Земли солнечной радиации приводит к большой неопределенности результатов измерений из-за нестабильности свойств атмосферы и альбедо Земли.

и 532 нм. Согласно работе [8], использование изотропных источников для калибровки обладает тем преимуществом, что результаты измерений оказываются менее чувствительными к относительному углу между источником и наблюдателем. Из-за отсутствия таких идеальных источников в настоящее время используются высотные баллоны, на которых могут быть установлены либо кварце-вые-вольфрамовые-галогеновые лампы, либо светоизлучающие диоды, либо плазменные лампы.

Вариант построения платформы, носимой баллоном, показан на рис. 1 а , 1 б [8].

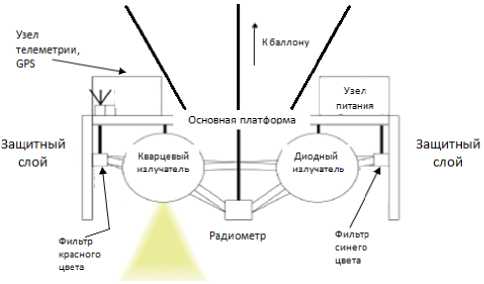
1.    Существующий метод Наиболее перспективным в решении данного вопроса следует считать использование источников оптической радиации, установленных на высотных баллонах и ракетах. Например, если установить вольфрамовую лампу с мощностью 25 Вт, излучающую оптическую радиацию мощностью 1 Вт в диапазоне 390-780 нм изотропно во всех направленных, то на Земле получим точечный источник со звездной величиной 12,5. Согласно [7], альтернативой изотропно излучающей и в принципе нестабильной вольфрамовой лампе является лазерный источник, установленный на каком-либо носителе, возможно, на спутнике, или на специальных высотных баллонах. Дивергенция лазерного луча равна нескольким миллирадианам, и магнитуда такого орбитального лазера на уровне Земли определяется следующим выражением: Рис. 1. Схематическое представление платформы, носимой баллоном: а - вид сбоку; б - вид сверху m -2,5log I _P 101 h2 d2 - 20,1 где Р – мощность лазера в милливаттах; h – высота орбиты спутника, на котором установлен лазер; d – среднеквадратическое отклонение дивергенции лазерного луча в миллирадианах. При этом допускаем, что апертура телескопа намного меньше, чем среднеквадратическое отклонение дивергенции луча на уровне Земли. Согласно [7], разработана программа ALTAIR, согласно которой для калибровки наземных микротелескопов используются диодные лазеры с длинами волны 639 нм, 690 нм, 440 нм 2. Предлагаемый метод Основной недостаток баллонного метода калибровки наземных микротелескопов - низкая достоверность результатов калибровки из-за проведения измерений на одной высоте полета и использования различных типов источников света, несогласованных по спектральным характеристикам. Предлагаются следующие изменения в конструкции платформы: 1. Замена всех источников на однотипные лазерные излучатели.

АППАРАТЫ 1/1

Том 4

• 2.    Проведение калибровочных процедур на различных высотах.

Вышеуказанное первое нововведение может обеспечить некоторую изотропность излучения за счет дивергенции однотипный лазерных лучей.

Второе нововведение позволит приобрести новый качественный показатель-признак верности проведенной калибровки в виде появления экстремума в суммарном калибровочном сигнале.

Несколько подробно остановимся на втором нововведении. Очевидно, что при предлагаемых нововведениях базовой формулой расчета оказывается выражение (1).

Если учесть, что измерения в предлагаемом методе проводятся на разных высотах в пределах 0: h max , то, условно переходя на непрерывную модель анализа, введем на рассмотрение функцию:

d = ф( h), (2)

показывающую зависимость дивергенции от высоты полета платформы. Далее можно предположить, что с увеличением показателя d также увеличится количество микротелескопов, которые будут охвачены оптическим следом лазерных лучей, исходящих от лазеров на платформе. С учетом вышеуказанного суммарную звездную величину одного излучателя платформы на высоте h оценим как:

Интегрируя (3) по всем h в пределах (0^ h max ), получим:

h                       _ max

тинт = - f 2,5 • k • h • logic ,2.2nx dh + o                  h ф (h)

^h max                                                        ⁽⁴⁾

+ J C•hdh .

Для решения задачи вычисления оптимальной функции ф( h ) рассмотрим следующее ограничительное условие:

h max

|ф( h) dh = C1,                (5)

о где С 1=const. С учетом выражений (4) и (5) сформируем функционал безусловной вариационной оптимизации F, который представляется в виде суммарного калибровочного сигнала:

max

F = -J 2,5 ■ к ■ h ■ logio

P dh + h2ф2(h)

h                       h max                     max

+ J C ■ hdh + X J ф(h)dh - C

m_y = -2,5 • k • h • log_in —---- dh+ + C ( h ).

²                     h ²ф( h )²

(3)       Хорошо известно [9; 10], что решение задач типа (5) и (6) должно удовлетворить условию:

d ^

P               Г          1

2,5• k• h• logw+ C(h) + Х[ф(h)-C1 ] [ h2Ф2(h)                       JI

d (Ф( h))

= 0.

Из условия (7) получим следующее выраже-      Таким образом, при решении (12) целевой

ние:

функционал (6) достигает экстремума. Для опре- 5 .    k . h                          деления типа экстремума достаточно определить (ИА In 10 + ^ = 0.              (8) знак второй производной интегранта в (6) по ф( h ) v '                               и убедиться, что она всегда отрицательна, т. е. при Из (8) находим:                           решении (12) функционал цели (6) достигает мак- -5⋅ k ⋅ h                     симума. ϕ( h ) =       .             (9)       Обладающий таким свойством суммарный ^" ln 10                    калибровочный сигнал, количественно определя- С учетом выражений (5) и (9) имеем:        емый выражением (4), может быть использован в качестве экстремального показателя верности max 5 ⋅ k ⋅ h                  (10) проводимой калибровки микротелескопов. ∫ λ⋅ln10        1 . 0                            3. Модельные исследования Из (10) находим: - 5 , к , h 2                           Проведем модельное исследование для про- λ =         max .             (11) верки верности полученного результата. 2 C 1 ⋅ ln 10                          Методика проверки состоит в следующем. С учетом выражений (8) и (11) получим:          1. Определяется пара функций, отвечающих 2 ⋅ C ⋅ h                  условию (5). Одной из этих функций выберем ф ( h ) =   2   .             (12) функцию (12). Вторую функцию определим из ус- h max                        ловия:

где

h max

| ф₂( h ) dh = C_x ,              (13)

S , ( h ) = - h • logio-7,            (21)

^A ■ ^hm

1         2    ,

_{A =} 2 C 1 h_m

Можно показать, что если выбрать φ2 в виде линейной функции

2CX A • h Ф2( h) =  ' —^, hm   hm

5 ₂( h ) = - h • log        '"             (22)

h ² (2 - h )²

в интервале h =0^1.

Построенные графики S 1 ( h ) и S ₂( h ) приведены на рис. 3. Как видно из приведенных на рис. 3 графиков, площадь участка под кривой 1 значительно больше площади участка под кривой 2. Следовательно, функционал цели (6) при решении (12) получает большее значение, чем при выборе функции (16). Таким образом, подтверждается оптимальность решения (12).

то условие (13) выполняется (рис. 2).

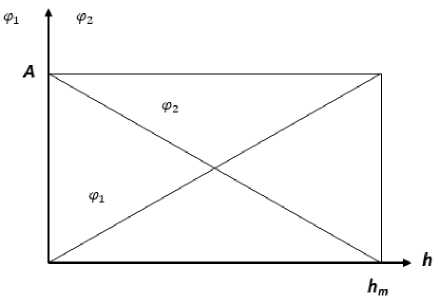
Рис. 2. К выбору функции φ2

2. Исследуется экстремум первого целевом функционале (6) без постоянных телей, т. е.:

hm

F ₁ =- ∫ h ⋅log₁₀

^P    dh .

h ²ϕ² ( h )

Для этого ставим Получим:

решение (12)

в

hm

F ₁(ϕ₁)=- ∫ h ⋅log₁₀

^{P ⋅ h} max _{dh .} 4 C ₁ ² h ⁴

Ставим выражение (16) в (17). Получаем:

hm

^F 1 ⁽9 2 ) = ^- J ^h " log io

P

2 ( 2 C i    A - h )²

h     h

У h m     h m 2

dh .

Следует построить графики интегрантов в (18) и (19) и далее визуально оценить площади под ними.

Примем модельные величины:

A=1; h_m =1; C 1 = 1; P =1.        (20)

Таким образом, следует построить графики функций:

члена в множи-

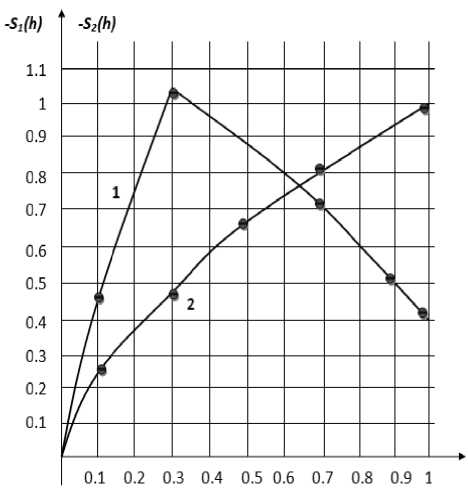
Рис. 3. Графики функций S 1 ( h ) и S ₂( h ). Принятые обозначения: 1 - график функции S 1 ( h );

2 - график функции S ₂( h )

Заключение

Показано, что требование дальнейшего повышения точности наземного отслеживания орбитальных спутников диктует необходимость по-

вышения точности калибровки используемой для этой цели сети микротелескопов. Для этой цели используются внешние стабильные источники излучения в виде лазера, устанавливаемые на баллонных платформах, поднятых на одинаковую высоту.

Однако, осуществление калибровки всего лишь на одной высоте может привести к недостаточной величине отношения сигнал/шум, а использование излучателей с различными спектральными характеристиками может усложнить требуемую методику анализа. Нами предложено использование однотипных лазеров и проведение

КИЕ АППАРАТЫ И

Том 4

калибровки на множестве высот поднятия платформ. При этом если соблюсти принятое ограничительное условие, то оказывается, что суммарный калибровочный сигнал при соблюдении некоторого оптимального условия может достичь экстремального значения. Предлагается использовать указанное свойство для проверки правильности проведенной процедуры калибровки.