Вопросы синтеза динамической модели для контроля и диагностики пилотажно-навигационных комплексов летательных аппаратов

Современные диагностические комплексы систем бортового оборудования прошли долгий путь развития, совершенствования, и представляют из себя мощные многофункциональные программируемые системы, способные выполнить в составе одного комплекса широкий спектр диагностических тестов, применительно к разным типам бортового оборудования. Несмотря на высокий технический уровень современных диагностических средств некоторые вопросы диагностики систем пилотажно-навигационного комплекса (ПНК) современных летательных аппаратов (ЛА) в силу специфики выполняемых задач остаются не решенными.

Анализ процессов контроля и диагностики ПНК показал, что лётные испытания выявляют достаточно высокий процент неисправностей, связанных с функционированием ПНК в целом в реальных динамических условиях. Однако лётные испытания не дешевы, и каждый авиапроизводитель стремится уменьшить объём внеплановых (повторных) вылетов для отработки обнаруженных дефектов. Решение этой задачи возможно на базе динамической модели всего пилотажно-навигационного оборудования как единого комплекса. Для создания такой модели и её реализации в рамках

динамической системы контроля и диагностики в наземных условиях необходимо решить ряд задач. Это позволит снизить объём летных испытаний и как следствие производственных затрат, при этом значительно повысить качество авиационной техники, обеспечив безопасность полётов.

Данная статья посвящена одному из центральных вопросов - синтезу динамической модели систем ПНК для решения задач диагностики на базе таких математических инструментов как теория образов У. Гренандера [1] и теория тензорного анализа Г. Крона [2]. Подобному подходу к решению задач диагностики посвящены труды А.Н. Коптева, В .А. При-лепского, Д.В. Гольдена, В.И. Сагунова, Г.М. Загрутдинова, Б.Г. Соловьева.

Под динамической моделью будем понимать множество регулярных конфигураций р(k) [1], где k - набор правил и ограничений, а само множество р(k) является пространственно-временным образом полной структуры ПНК, отражающим все пилотажные и навигационные задачами, выполняемыми комплексом в полёте. Таким образом, задача аппаратных средств диагностики в общей постановке сводится к сравнению полученного образа ПНК с реально существующим оригиналом. Представлением конкретной пилотажнонавигационной задачи является конфигурация ci е p(k) обладающая составом и структурой. Состав всякой конфигурации ci есть набор: Ci = {g 1,g2,gз...gn}, где g - образующая [1], являющаяся интерпретацией стандартных составных блоков и агрегатов моделируемых систем ПНК. Структура конфигурации с представляет собой множество σ соединений, существующих между всеми или некоторыми связями ω(gi) образующих, входящих в её состав. Множество σ можно задать с помощью квадратной матрицы инцидентности порядка Σω(gi), в которой единицы и нули указывают наличие или отсутствие соединения в определённых парах связей, которая ожжет быть представлена дельтой Кронекера [2].

На основе обобщённого понятия образующей и понятии о конфигурации, с учётом правил и ограничений, строим конфигурации для представления определённых контуров систем ПНК. В качестве примера конфигурации можно привести задачу поддержания ЛА на заданной траектории полёта на примере самолёта Ан-140 (рис. 1). В рамках решения поставленной задачи системы ПНК взаимодействуют следующим образом. Траектория полёта со всеми промежуточными пунктами предварительно программируется в бортовой системе приёма спутниковой навигационной информации СН-3301. По сигналам СНС ГЛОНАСС и GPS, а, также используя значение истинной воздушной скорости ( V ист ) от системы ИК ВСП и текущего курса ( φ тек ) от БСФК, аппаратура СН-3301 формирует и выдаёт в САУ сигнал заданного угла крена γ зад ⁼ f(z,z ^& , Δ ЗПУ ) , где: z & = W z – составляющая вектора путевой скорости, β – угол сноса. Получая значение γ зад , вычислитель САУ определяет закон управления по каналу крена δ эл = f ( γ зад ). Самолёт совершает эволюции, приводящие к возврату на траекторию полёта, определяя тем самым обратную связь всего процесса регулирования.

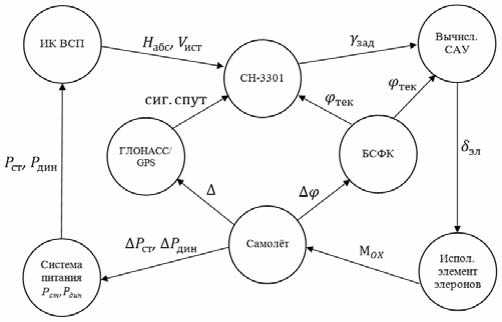
Рис. 1. Стабилизация ЛА на заданной траектории

При составлении образов любых систем бортового комплекса оборудования очевидно, что в составе полного изображения [1] временным изменениям подвержены только показатели связи введенных образующих:

β ij = f(t) .

Таким образом, введём дополнительное условие: X = R ³ x R^t , где R^t – пространство времени. В новом опорном пространстве R^t будем рассматривать полное множество показателей связи как множество временных образов. В целях синтеза временного образа введём три новых вида образующих и рассмотрим их свойства.

up up up

• 1.    g i ( f i ( t), ^τ i ) – интерпретация увеличения, возрастания значения показателя связи β i по отношению к исходному состоянию. Данная образующая характеризуется двумя признаками: f i^up (t) - функция времени, определяющая характер процесса восстановления. В качестве f_i ^up (t) может выступать любая возрастающая функция, в том числе и скачёк. Второй признак ^τ i^up характеризует длительность процесса возрастания в каких-либо единицах времени.

• 2.    g i ( f i    ( t), ^τ i    ) – интерпретация

• 3.    g_i ^con ( Y_i, τ _i ^con ) , признаками которой являются длительность неизменного состояния Y _i , τ _i ^con - текущее значение, существующее в con

dow dow dow

уменьшения, снижение значения βi от уровня исходного состояния. Образующая gidow является противоположной в отношении образую-up щей gi и характеризуется аналогичными признаками: – законом fidow(t) и длительностью τidow процесса уменьшения. Двух введенных образующих недостаточно для формирования конфигурации временного образа. Не хватает ключевого звена – точки начала отсчёта, стартового уровня, характеризующего текущее положение показателя связи βi. Эту роль выполняет образующая.

течении времени τ _i и являющееся значением показателя связи. На базе заданных образующих получена обобщённая временная конфигурация (рис. 2).

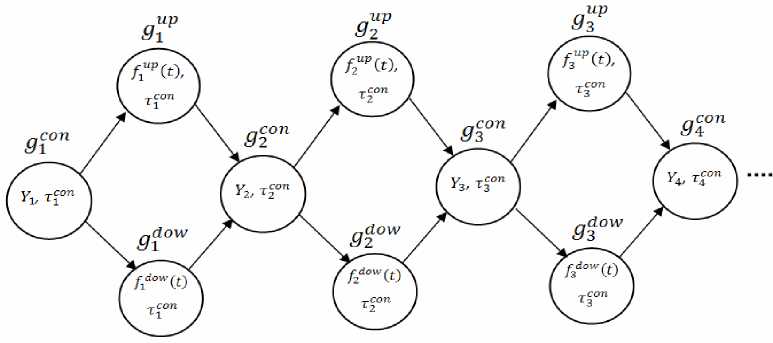
Рис. 2. Обобщённая временная конфигурация

Любой процесс начинается с исходного положения У/, которое существовало сколь угодно долгое время Tc° (образующая gcn). Далее наступает изменение У либо в сторону увеличения по закону flup (t), либо в направлении уменьшения по закону fi°w (t). По истечению времён соответственно либо т“р, либо Т0 параметр У/ приобретает новое значение У2, в котором будет находиться в течении вре-con мени Т2 (образующая gcn). На следующей итерации фигурантами подобного процесса выступают образующие g2р, g2°, g™" и т.д. В общем случае при t^^ временная конфигурация (рис. 2) устремляется в бесконечность:

^: 0(тир+т^+td=^

В частных случаях конфигурация (рис. 2) имеет количество из n итераций, в рамках которых завершается представляемое действие, происходящее в течении времени тп у” /-up , -d°w ,   con

^i=0(Ti + Ti + Ti   ) = Tn

.

Сочетание конфигурации типового процесса (рис. 1) и временной конфигурации (рис. 2) позволяет формировать пространственновременные образы, применяемые в целях динамического моделирования систем ПНК любых ЛА при контроле и диагностике.

С общих позиций задачи диагностики можно свести к следующей постановке (рис. 3). Аппаратные средства контроля и диагностики (АСКД), скомплектованные в единый проверочный комплекс, имеющий в своём составе все необходимые элементы, обеспечивающие формирование и подачу оптимального множества воздействий:

X = { x₁,x₂,x₃,...,x_n } ,

на вход проверяемых систем и агрегатов ПНК и на вход, синтезированной в виде пространственно-временного образа, модели ПНК.

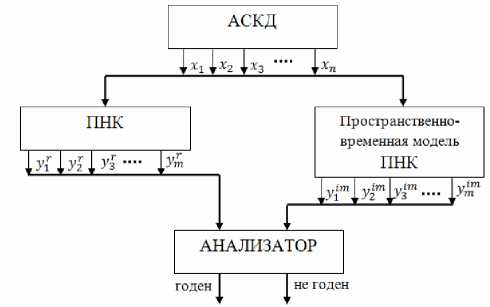
Рис. 3. Алгоритм диагностики

Отрабатывая входные возмущения сис-

,...

темы и агрегаты ПНК формируют множество:

УГ = {yl ,У2,Уз,-,yrm } выходных парамет ров. Так же пространственно - временная модель, испытывая деформации [1], формирует Yim im im im im

= {У1 ,y2 ,y3 ,...,ym }, являющееся идеальной реакцией, соответствующей полностью исправному ПНК. Далее мно-im r жества У и У сравниваются в анализаторе, который выполняет операцию: yr - yim > Ai, где Ai - пороговое значение, заданное для каждого контролируемого параметра технической документацией на объект контроля и диагно- стики.

Выводы: разработанный алгоритм контроля и диагностики обладает большой гибкостью и функциональностью, так как разработчик диагностических тестов вправе сам выбирать состав множество исходных воздействий X. И поскольку пространственно-временная модель ввиду полного соответствия способна отразить все режимы работы ПНК, то на базе одних и тех же АСКД, используя различные 1. модели, можно выполнять как оперативные 2 тесты, так и полную динамическую диагности ку современных пилотажно-навигационных 3. комплексов для оценки их состояния.