Вопросы внешней баллистики полета контейнера для доставки огнетушащих составов в контейнерах методом метания с применением установок пожаротушения стволового типа

К числу основных задач исследования установок пожаротушения стволового типа контейнерной доставки огнетушащих веществ [1] относятся определение дальности полета и проведение расчета траектории полета контейнера в виде капсулы на удаленное расстояние. В основе действия установки стволового типа лежит метод преобразования энергии сжатого воздуха в высокоэнергетический импульс, позволяющий осуществлять метание огнетушащего вещества в контейнере на удаленное расстояние без применения взрывчатых веществ и подавлять очаг пожара без потерь огнетушащего вещества при доставке в зону горения.

Проведение теоретических исследований

Первоначально расчет траектории полета контейнера выполним без учета сопротивления воздуха. При расчете принимаются следующие допущения:

• 1)    контейнеры, используемые для проведения испытаний, имеют форму обтекаемой конструкции в виде снаряда, рис. 1;

• 2)    окончательная скорость контейнера равна его начальной скорости;

• 3)    угол падения равен углу бросания;

• 4)    не учитывается шарообразность Земли и ее вращение.

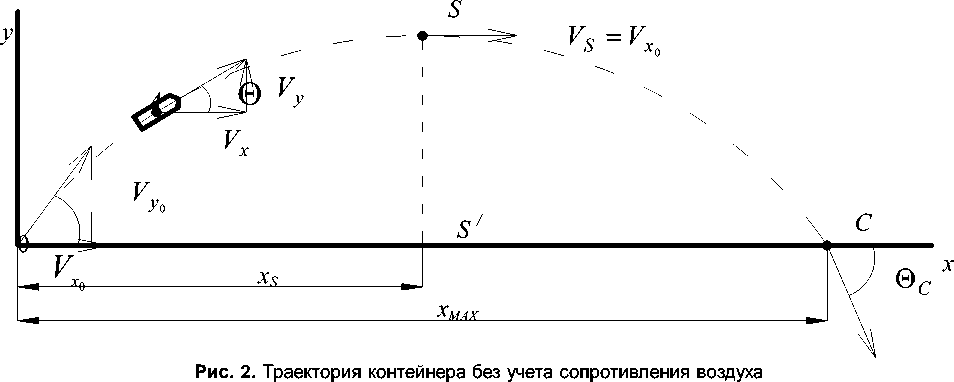
При заданных допущениях на контейнер с огнетушащим веществом после вылета из канала ствола установки действует сила тяжести, ускорение свободного падения g = 9,81 м•с^-2. Контейнер описывает кривую в виде параболы, рис. 2.

Уравнение функции траектории полета контейнера без учета сопротивления воздуха при постоянных значениях величины и направления силы тяжести описывается уравнением с учетом и влиянием на полет контейнера сил тяжести [3]

y = x ⋅ tg ( Θ ₀) -

g ⋅ x

2 ⋅ V 0 ² ⋅ cоs ² ( Θ 0 )

(1),

где x , y – координаты центра масс контей-

Рис. 1. Имитаторы контейнеров, используемые для проведения испытаний

нера; V0 – начальная скорость метания кон- тейнера, м•с-1; Θ0 – начальное значение угла полета – угол бросания, град; g – ускорение свободного падения, м•с-2.

С учетом преобразования формулы (1) и принятых вышеуказанных допущений определяется максимальная дальность полета контейнера х_MAX как [4]

V ₀ ²

^XMAX = . (2).

g

Параметру дальности полета х _MAX соответствует угол бросания, называемый углом максимальной дальности. Для случая полета без учета сопротивления воздуха 0 ₀ = 45° [3].

Однако параболическую теорию движения контейнера без учета сопротивления воздуха на практике можно приближенно принять при расчете полета на небольшие расстояния (10 - 15 м) при условии небольшой начальной скорости полета контейнера. Учитывая сопротивление воздуха при движении контейнера возникают силы давления Р и трения ф , противодействующие её движению (рис. 3).

За контейнером образуется область завихрений воздуха, в которой давление понижено, что приводит к дополнительному торможению полета. Суммируя действующие силы, образуется результирующая аэродинамическая сила сопротивления воздуха _R .

В процессе полета положение продольной оси Ок - Ок контейнера, рис. 4, меняется и не имеет постоянного совпадения с направлением вектора скорости V полета контейнера, периодически отклоняясь от направления V . Вследствие чего результирующая сила _R в общем случае не совпадает ни с осью контейнера, ни с направлением скорости его полета (рис. 4). Поэтому силу _R принимаем как сумму трех составляющих сил: силы лобового сопротивления R _x , подъемной силы R y , перпендикулярной R _x и лежащей в вертикальной плоскости; боковой силы R _z , перпендикулярной первым двум (рис. 4).

При устойчивом движении контейнера в процессе полета подъемная R y и боковая R_z силы меньшее значение по отношению R _x . Подавляющее влияние на движение контейнера и на траекторию полета оказывает сила лобового сопротивления R_x . Для ее вычисления воспользуемся формулой [3]

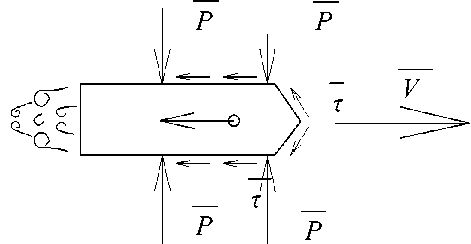
Рис. 3. Влияние внешних действующих сил сопротивления воздуха на контейнер во время полета

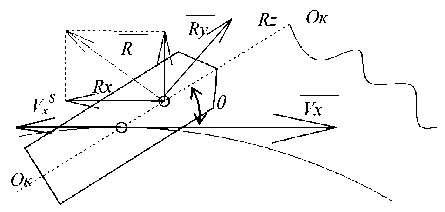
Рис. 4. Силы, действующие на контейнер при полете в воздушной среде

R x =        • S m • C x ,         (3)

, P- V „

I x = ~ S M • C x .        (5)

2 • m где р = р(у) - массовая плотность воздуха, зависящая от высоты полета у, наземное значение её ρ0N при нормальных (средних) ме-

теорологических условиях принимается равным 1,206 кг • м^-3; V_x – проекция вектора скорости полета контейнера в заданный момент

Далее рассмотрим элементарный участок полета контейнера, на котором его скорость V постоянна. Данный участок контейнер пролетит за элементарное время Д _т . При этом, ускорение полета контейнера изменит-

времени на ось x , м•с^-1;

_ п • d²

SM =   4

– пло-

щадь поперечного сечения контейнера; C_x – коэффициент силы лобового сопротивления.

Коэффициент силы лобового сопротивления является функцией от скорости и называется законом C_x ( V ) сопротивления воздуха. Для контейнеров законы сопротивления имеют совпадающие значения. Типовой график функции C_x ( V ) показан на рис. 5, где видно, что наибольшее значения C_x достигает в точке, где V = a ( а – скорость звука в воздухе, она равна на уровне земной поверхности в среднем 340 м•с^-1). При малых скоростях полета ( V = 250 м•с^-1 и менее) C_x ( V ) практически не изменяется и равен для тел по форме в виде снаряда от 0,29 до 0,35.

Согласно первому закону Ньютона, ускорение (замедление), создаваемое силой лобового сопротивления будет равно

R

I x = —,             (4)

m где m – масса контейнера, кг. Подставляя (3) в (4), получим

C x ( V )

0,31

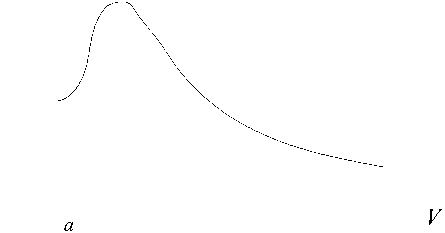
Рис. 5. График расчета коэффициента лобового сопротивления полета контейнера

Ix ся на значение д— для элементарного участ-

ка траектории

I x

Д т

р - V² V с

• S M C x .

2 • m

Считая, что коэффициент сопротивления воздуха в любой точке траектории полета контейнера постоянен при скорости полета контейнера менее 250 м/с, интегрируя выражение (6), получим

V S = р-- S m • C x • т + a ,   (7)

2 • m

где V_x^S - величина, на которую уменьшается значение скорости, рассчитываемой без учета сопротивления воздуха, при учете коэффициента сопротивления воздуха; A - постоянная интегрирования, определяется из условия, что при _т = 0, V xS = V x_o , для V x_o = 0 значение A = 0.

Зная V_x^S , можно определить скорость полета в любой момент времени

V x ^R£Z = V_x - V_x^s , (8) где V_x^REZ – величина скорости, для расчетного момента времени с учетом сопротивления воздуха; V_x – величина скорости, для расчетного момента времени без учета сопротивления воздуха; V_x^S – величина, на которую уменьшается значение скорости, V_x при учете коэффициента сопротивления воздуха.

Подставляя (7) в (8) и выражая V через V_x , получим общую формулу, описывающую зависимость проекции результирующей скорости на ось ОХ от времени полета контейнера

V xREZ = V x - , ^P ' V', _n • S m • C x • T , (9).

2 • m • cos 0

L_x ,= к • ln x , i

V^x , i ^{- 1}

Разбивая траекторию полета контейнера на участки, можно определить проекцию скорости на ось ox контейнера в каждый момент времени, принимая движение контейнера равнозамедленным. Проекция скорости на ось ox в каждой точке при этом случае будет равна

P • V 2 i

V i = Vx i -i-- x ^, i 1 • Sm • Cx • T , (10), x , I         x , I                                                       x I

2 • m • cos 0

V .

V v    x , i

A      A

+ L i - 1 • ^{cos 0}

7      7

. (13)

Учитывая (1) выведем зависимость высоты полета контейнера от времени полета через дальность, скорость и угол полета с учетом постоянного коэффициента сопротивления воздуха

y i ^SV

или

= L x , i • tg ^{0 -}

g • L x , i

2 • V. 2 • cos 2 0 x , i

(14),

где V_{x , i} – проекция скорости движения контейнера ось ox в момент времени τ_i ( i -й участок), м • с^-1; V x , i - 1 - проекция скорости контейнера ось ox на предыдущем участке (участок i -1).

Используя формулу, определяющую дальность полета на прямолинейном участке полета [5], определим путь, пройденный контейнером за время τ_i

y i ^SV

/

к • ln

V x , i ^{- 1}

\

V

g •

• tg 0 -

V    x , i 7

(     ( k •ln

VV

+ L i - 1

V x, i 1

V x , i

• cos 0 •

AA

+ L , - ,

L i = к • ln

(v A

V x , i ^{- 1}

2 • V. 2 • cos 2 0 x , i

V     i , i 7

+ L - 1 ,

V7

где: L i - 1 - путь пройденный контейнером за время T i - 1 , м; к - эмпирический коэффициент, определяемый экспериментальным путем.

Проекция пути пройденного контейнером за время τ_i на ось ox равна

L x , i = L- cos 0 .           (12)

Подставляя (10) в (11), получим

На основе расчетных формул (11), (12), (13) разработана программа с применением пакетов EXCEL и MATHCAD, позволяющая рассчитать с заданной точностью высоту полета контейнера в любой момент времени и с ее помощью построить графики зависимости высоты полета контейнера от дальности полета (рис. 6) и угла наклона ствола, например, для угла бросания 70, рис. 6.

Исходные параметры, принятые для рас-

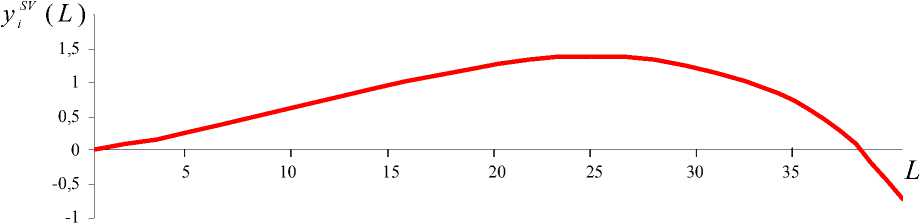
Рис. 6. График определения высоты полета контейнера в зависимости от дальности полета, угол бросания контейнера 7^о

чета высоты полета в зависимости от дальности с использованием ЭВМ: 1) начальная скорость полета капсулы V ₀, _{м ⋅ с} ^-1 ; 2) угол наклона ствола установки к горизонту Θ _i , град.; 3) плотность окружающего воздуха ρ , _{кг ⋅ м} ^-3 .; 4) коэффициент сопротивления воздуха С_Х , _с ^-1 .; 5) диаметр контейнера d , м.; 6) масса контейнера m , кг.; 6) время полета τ от точки вылета до точки падения, с.

В результате проведения расчетов получены параметры траектории полета контейнера с учетом сопротивления воздуха.

Проведение экспериментальных исследований

В соответствии с постановкой задачи определения траектории полета контейнера, максимальной дальности полета и поведения контейнера в воздухе проведены экспериментальные стендовые испытания. Допущения, принятые при проведении эксперимента: 1) коэффициент сопротивления воздуха имеет постоянное значение для каждого контейнера; 2) отклонение контейнера от вертикальной плоскости минимально.

Исследование процессов, происходящих с контейнером в виде капсулы при полете в воздухе проводилось на испытательном стен-

Рис. 7. Экспериментальный стенд для проведения испытаний стволовой установки доставки огнетушащих веществ в контейнерах методом метания де стволовой установки контейнерной доставки огнетушащих веществ (рис. 7) с использованием имитаторов контейнеров, выполненных из пластичного материала (рис. 1). Обеспечивается регулировка и установка угла наклона оси ствола. Угол наклона ствола задает угол бросания контейнера.

Характеристики контейнеров, применяемых для проведения испытаний, представлены в табл.

Первая серия экспериментов проводилась с установкой стенда в закрытом помещении. Вторая серия экспериментов осуществлялась с установкой стенда на испытательной полосе, застеленной упругим резиновым покрытием (рездором).

Результаты эксперимента фиксировались и отрабатывались в следующей последовательности:

• -    проведение выстрела контейнера на установке;

• -    проведение цифровой видеосъемки от момента начала полета контейнера до момента падения контейнера;

• -    контроль и фиксация времени полета электронным секундомером и по результатам просмотра видеозаписи;

• -    определение дальности полета в точке падения контейнера в конце траектории полета контейнера;

• -    определение вращения контейнера относительно оси или центра тяжести в горизонтальной и вертикальной плоскости по результатам просмотра видеозаписи;

• -    расчет деривации контейнера в точке падения (отклонение от оси ствола при полете) определялся по результатам замера отклонений;

• -    определение скорости вылета и полета контейнера путем просмотра видеосъемки в замедленном режиме при движении контейнера вдоль мерной рейки, прикрепленной к стволу установки, проведение расчетов.

Анализ результатов теоретических исследований и проведенных экспериментальных стендовых испытаний

С помощью программного обеспечения MATHCAD построены графические зависи-

Таблица. Характеристики контейнеров

№ капсулы	Длина капсулы, мм	Диаметр капсулы внешний, мм	Масса капсулы, кг	Коэффициент центра масс
1.1*	125	29	0,0704	0,44
1.1*	125	29	0,0704	0,44
1.1**	125	29	0,0704	0,44
1.2*	125	28	0,0658	0,45
1.2**	125	28	0,0658	0,45
1.3*	125	27	0,0605	0,46
1.3**	125	27	0,0605	0,46
1.4*	125	26	0,0546	0,46
2.1*	135	29	0,1222	0,45
2.1*	135	29	0,1222	0,45
2.1*	135	29	0,1222	0,45
2.1*	135	29	0,1222	0,45
2.2*	125	28	0,0983	0,49
2.2*	125	28	0,0983	0,49
2.3*	135	27	0,1	0,48
2.3*	135	27	0,1	0,48
2.4*	125	26	0,0817	0,52
2.4*	125	26	0,0817	0,52
3.1**	124	29	0,1037	0,46
3.1**	124	29	0,1037	0,46
3.1**	124	29	0,1037	0,46
3.1**	124	29	0,1037	0,46
3.1**	124	29	0,1037	0,46
3.1**	124	29	0,1037	0,46
3.1**	124	29	0,1037	0,46
3.1**	124	29	0,1037	0,46
3.1**	124	29	0,1037	0,46
3.2**	124.3	28	0,0996	0,47
3.2**	124.3	28	0,0996	0,47
3.3**	124.1	27	0,0955	0,47
3.3**	124.1	27	0,0955	0,47
3.4**	124	26	0,0897	0,48
4.2**	125	28	0,105	0,46
4.3**	125	27	0,078	0,44
4.4**	125	26	0,1117	0,44
4.4**	125	26	0,1117	0,44
5.1**	124	29	0,13	0,43
5.1**	124	29	0,13	0,43
5.2**	124.3	28	0,113	0,43
5.2**	124.3	28	0,113	0,43
5.2**	124.3	28	0,113	0,43
5.2**	124.3	28	0,113	0,43
5.2**	124.3	28	0,113	0,43
5.3**	124.1	27	0,1223	0,48
5.4**	124	26	0,103	0,43

Примечание: 1. * – первая серия экспериментов 2. ** - вторая серия экспериментов. 3. Коэффициент центра масс Kcm вычисляется по формуле Kcm

lcm

, где l - расстояние от торца капсулы до центра масс, м; lk        cm lk - полная длина капсулы, м мости дальности полета контейнера от его внешнего диаметра, давления, подаваемого в турбину установки воздуха, угла подъема ствола установки в вертикальной плоскости, массы контейнера, коэффициента центра масс. Графики построены следующим образом: а) на координатные оси нанесены точки – результаты расчетов и экспериментов, б) на нанесенные точки наложены полиномиальные линии тренда. Степень каждого полиномиального уравнения подбирается исходя из минимального среднеквадратичного отклонения. При этом истинная функция определяется по уравнению вида f = a. + af + a,f2 +...+a fn. (15) ист 0 1 1 2 2 n n где an – коэффициенты полиномиального уравнения; n – степень полиномиального уравнения. На графиках были приняты следующие условные обозначения:

v : Результаты зкспержлентов О О : Результаты расчетов

: Линия результатов экспериментов ; Линия результатов расчетов

В процессе проведения первой серии экспериментов была определена максимальная дальность полета контейнеров 1,1 - 2,4 (табл. 1) при подаче воздуха 0,75 МПа и угле наклона ствола установки 7 градусов. Дальность полета составила 41,9 м (капсула 1.1, диаметр 29 мм, длина 125 мм, масса 70,4 г, коэффициент центра масс 0,44). Установлены для первой серии испытаний зависимости дальности полета контейнера от величины зазора между наружной поверхностью контейнера и внутренней стенкой ствола установки, рис. 8, массы контейнера, рис. 9.

Анализ графических зависимостей показал, что при уменьшении диаметра капсулы (увеличении зазора) дальность полета контейнеров снижается. Полученные значения дальностей полета контейнеров удовлетворительно совпадают с расчетными данными. Это позволило провести исследования при доставке контейнеров на удаленное расстояние методом метания с требуемой точностью.

В результате проведения второй серии экспериментов были определены закономерности при метании контейнеров 1.1 - 1.4, 3.1 - 3.4, 4.2 - 4.4, 5.1 - 5.4 была достигнута максимальная дальность полета контейнеров 104 м – (контейнер 3.1: диаметр 29 мм, длина 124 мм, масса 103,7 г, коэффициент центра масс 0,46, давление воздуха 0,98 МПа, угол наклона оси ствола 300).

В ходе проведения второй серии экспериментов были установлены зависимости дальности полета контейнера от подаваемого давления сжатого воздуха, величины зазора между поверхностью контейнера и внутренней стенкой ствола установки, массы контейнера, угла наклона ствола установки в вер-

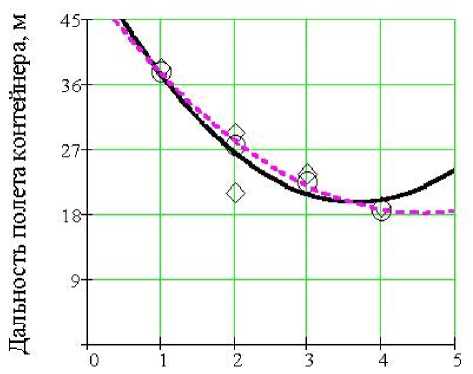
Зазор, мм

Рис. 8. График зависимости дальности полета контейнера от зазора между контейнером и внутренней полостью ствола при метании контейнеров:

2.1-2.4; давление 0.75 МПа;

угол наклона оси ствола установки 70

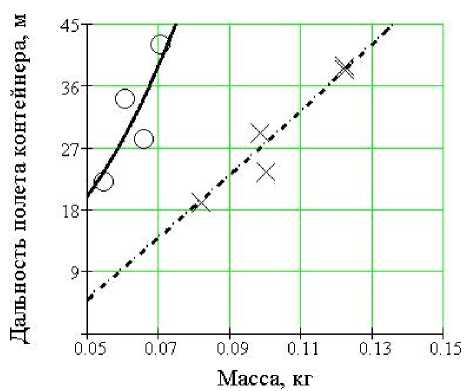
Рис. 9. График зависимости дальности полета контейнеров от их массы при давлении 0.75 МПа; угол наклона оси ствола установки 7^о: О О О - метание контейнеров 1.1 - 1.4;

Х Х Х - метание контейнеров 2.1 - 2.4

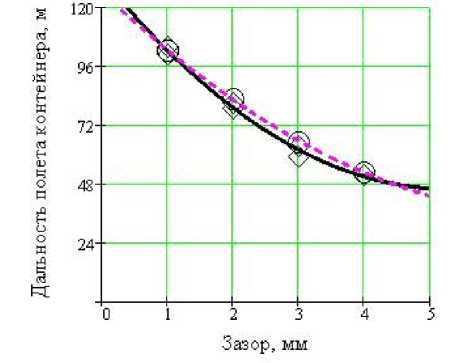
Рис. 10. График зависимости дальности полета контейнера от зазора между контейнером и внутренней полостью ствола при метании контейнеров: 3.1 - 3.4; давление 0,98 МПа;

угол наклона оси ствола установки 30о

Зазор, мм '

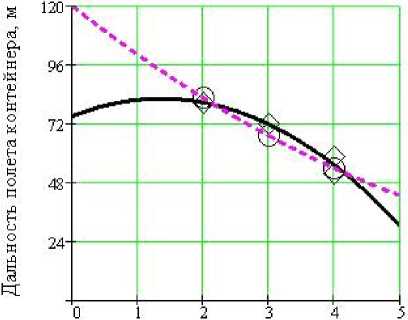
Рис. 11. График зависимости дальности полета контейнера от зазора между контейнером и внутренней полостью ствола при метании контейнеров: 4.2 - 4.4; давление 0.98 МПа; угол наклона оси ствола установки 30⁰

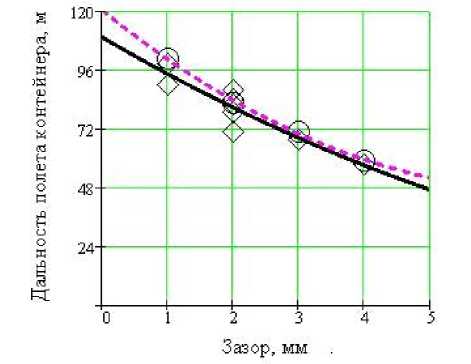
Рис. 12. График зависимости дальности полета контейнера от зазора между контейнером и внутренней полостью ствола при метании контейнеров: 5.1 - 5.4; давление 0.98 МПа;

угол наклона оси ствола установки 300

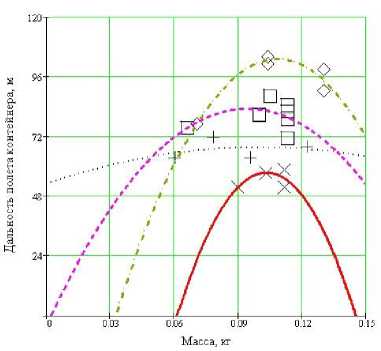
Рис. 13. График зависимости дальности полета контейнеров от их массы при давлении 0,98 МПа; угол наклона оси ствола установки 30^о , где Х Х Х – метание контейнеров диаметром 26 мм; + + + – метание контейнеров диаметром 27 мм; □ □ □ - метание контейнеров диаметром 28 мм; ◊ ◊ ◊ - метание контейнеров диаметром 29 мм

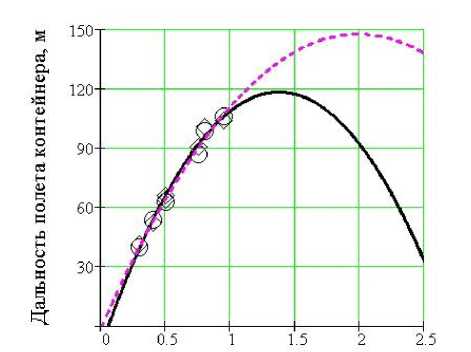
Подаваемое давление, МПа

Рис. 14. График зависимости дальности полета контейнера от давления, подаваемого воздуха при метании контейнеров:

3.1; угол наклона оси ствола установки 30о

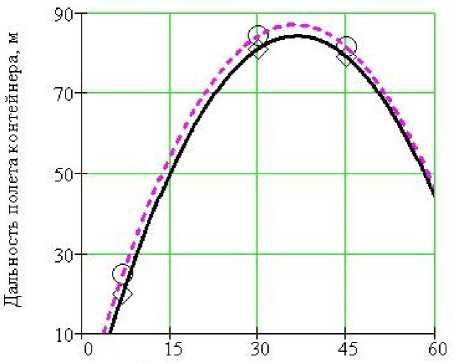
Угол подъема ствола, град

Рис. 15. График зависимости дальности полета контейнера от угла наклона ствола установки относительно горизонта при метании контейнеров: 3.1 - 3.4; давление 0.98МПа

тикальной плоскости по отношению к горизонту, коэффициента центра масс, графики зависимостей рис. 10 - 17.

Анализируя зависимость дальности полета имеющихся моделей контейнеров от зазора между их поверхностью и внутренней стенкой ствола установки в первой и во второй серии экспериментов, можно сделать вывод, что независимо от диаметра контейнера, его массы и длины зависимость имеет один и тот же вид для контейнеров типов 1.1 - 1.4, 2.1 - 2.4, 3.1 - 3.4, 5.1 - 5.4. Однако, для контейнеров типа 4.2 - 4.4 была получена линия экспериментов не вогнутая, а выпуклая. Расчетные значения показывают, что зависимости имеют общий характер изменения для всех модификаций контейнеров. Расчеты позволяют спрогнозировать дальность полета контейнеров каждой модели при изменении параметров.

Для второй серии экспериментов были построены графики зависимостей дальности полета от массы контейнеров (рис. 13 ), заданного угла наклона оси ствола 300. Данный график (рис. 13) дает возможность визуально определить характер зависимости дальности полета всех типов контейнеров от их массы, позволяет оценить эффективность доставки контейнеров различного диаметра. Наиболее эффективными являются контейнеры диаметром 29 мм (с увеличением массы была достигнута максимальная дальность 101-104 м), для диаметра 28 мм максимальная дальность – 88 м., для диаметра 26 мм максимальная дальность – 72 м. и диаметрf 26 мм максимальная дальность – 59 м. Причем максимальной дальности трех типов контейнеров (диаметром 26, 27, 29 мм) соответствовали массы 103, 113 и 137 грамм. Наиболее оптимальным диаметром для стенда экспериментальной установки обладал контейнер 29 мм, с наиболее эффективной массой – 115 – 120 грамм.

Определив контейнер, дальность полета которого при заданных условиях эксперимента составляла максимальное значение (контейнер 3.1), была проведена серия выстрелов с заданием различных значений давлений. Результаты аналитических расчетов и экспериментов показаны на рис. 14.

Анализируя графики (рис. 14, 15), можно сделать вывод, что график изменения дальности полета контейнеров при метании их с использованием установки при различном подаваемом давлении воздуха приближается к параболическому закону. Результаты теоретических расчетов удовлетворительно описывают зависимость дальности полета контейнера от подаваемого давления на отрезке 0,3 – 0,98 МПа, что позволяет утверждать о достоверности проведения расчетов. Это дает основание говорить о достоверности проведения расчетов и при увеличении давления более 0,98 МПа. Кривая аналитических расчетов дает возможность спрогнозировать максимальную дальность полета контейнера, которую можно обеспечить, используя результаты теоретических и экспериментальных исследований. Анализ графиков, в том числе, рис. 14, показывает, что при подаче давления воздуха до 2 МПа, дальность полета увеличивается до 150 м.

С применением контейнера 3.1 была проведена серия выстрелов при различных углах наклона ствола установки относительно горизонта, графическая зависимость дальности полета контейнера, рис. 15.

Исходя из результатов расчетов и подтверждающих их экспериментов максимальная дальность полета контейнеров на данной установке обеспечивалась с углом наклона ствола 35є и 30є (соответственно расчетное и экспериментальное значение).

Выводы

• 1.    Результаты проведенных исследований показали научную и практическую ценность применения методов контейнерной доставки огнетушащих веществ для тушения очагов сложных пожаров с возможностью метания контейнеров более 100 м.

• 2.    На основе обобщения современных знаний в области внешней баллистики впервые разработан метод расчета траектории полета контейнеров методом метания с принятыми допущениями.

• 3.    Разработана программа для расчета траектории полета контейнеров с учетом воз-

• действия на них силы сопротивления воздуха в зависимости от характеристик контейнеров и их начальной скорости полета.

• 4.    По результатам теоретических и экспериментальных исследований построены графические зависимости, позволяющие определить технические характеристики и достоверность результатов, характер изменения высоты полета контейнера в зависимости от дальности.

• 5.    Проведенные экспериментальные стендовые испытания подтверждают достоверность результатов аналитических исследований.

Исследования выполнены при содействии Российского фонда фундаментальных исследований по проекту № 05-01-96504.