Восстановление изображений на основе спектральной матричной нормы

Пусть изображение задано в виде неотрицательной вещественной матрицы A размером n х m с элементами ау е [0 a max ]. Будем считать, что изображение содержит искаженные пиксели. Координаты иска- женных пикселей известны, соответствующие элементы матрицы изображения равны нулю. Необходимо восстановить искаженные пиксели.

Для восстановления изображения применяют пространственные и частотные фильтры [1; 2].

Например, оценка значения пикселя a_ij в пространственном линейном сглаживающем фильтре определяется по формуле

^ a ˆ ij

rr

= EE

w p + r + 1, q + r + 1 a i + p , j + q ,

p=-rq=-r где r – радиус фильтра; wkl – весовые коэффициенты фильтра

2 r + 1 2 r + 1

wki ^ 0, E E wki = 1.

k = 1 l = 1

В случае равенства весов

an =------- ч ‘j (2 r + 1) 2

rr

V* V a.

Z—i Z—i i + p , j + q .

p =- rq =- r

Матрица W размером (2r +1) x (2r +1), составленная из весов wkl , называется ядром фильтра. Часто применяется гауссовский фильтр, ядро которого определяется функцией wkl

1 2πσ2

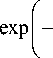
( k - r - 1)² + ( l - r - 1)² 2σ²

Радиус гауссовского фильтра r можно задать равным 3σ.

В данной статье описывается нелинейный гауссовский сглаживающий фильтр, построенный на основе спектральной матричной нормы.

Рассмотрим линейный фильтр (1). Заметим, что оценка значения aij может быть получена в результате минимизации нормы Фробениуса a у = arg min |\в( (5 )|F               (2)

матрицы B j ( 5 ) = sE - (2 r + 1)² W . Aj , где E - матрица с единичными элементами;

а, ••• ci, „ i - rr - r       I - rj+r

4 = ij ......

a i + rj - r ■" a i + rj + r

точка в выражении W . A_ij обозначает операцию поэлементного произведения матриц.

В вычислительной математике и методах анализа данных наряду с нормой Фробениуса применяется спектральная матричная норма [3], обладающая свойством грубости (робастности) по отношению к изменениям в элементах матрицы [4]. Заменим норму Фробениуса в выражении (1) на спектральную норму. Получим оценку

Ct ij = arg m i n | B ij ( s )||2 ,                 (3)

где B_ij – максимальное сингулярное число матрицы B_ij .

Фильтр (3) является нелинейным гауссовским фильтром. Вычислить значение aˆij несложно, по- скольку s – это скалярная переменная, принимающая значения в заданном интервале s е [0 a max ].

Качество восстановления изображения можно оценить по нескольким критериям:

– критерию отношения сигнала к шуму [2]:

d (A, .A) = 10log10 ^-^nm—;(4)

EE ( a j - a ij )² i = 1 j = 1

– критерию максимального отклонения:

dmax (A, ^i) = max max | aij - atij |;

– критерию на основе нормы Фробениуса:

A - .^

dF (A, ^A)=TAFF;(6)

– критерию на основе спектральной нормы:

A - )1

d 2(A, ^A) = AT'

Два последних критерия позволяют оценить качество восстановления изображения в процентном отношении.

В качестве примера рассмотрим черно-белое изображение, представленное в виде матрицы размером 400 x 600 (рис. 1). Элементы матрицы принимают значения от 0 до 255, что соответствует восьмибитному кодированию изображения. Файл с изображением взят с сайта

100           200            300           400           500           600

Рис. 1. Исходное изображение

Введем сле д ующие обозначения: A – исходное изображение; A – изображение с искаженными пикселями; A ^ˆ – восстановленное изображение. Искаженные пиксели имеют нулевое значение, что соответствует черному цвету (рис. 2).

Восстановление изображения выполнялось на основе линейного (ЛГФ) (рис. 3) и нелинейного гауссовских фильтров (НГФ) (рис. 4) с параметрами r = 2, о = 2/3.

100           200           300           400           500           600

Рис. 2. Изображение с искаженными пикселями

100           200            300           400           500           600

Рис. 3. Изображение, восстановленное на основе линейного гауссовского фильтра

Расчеты выполнялись в системе MATHLAB с использованием базовых функций чтения, записи и визуализации изображений [5].

Результаты расчетов, приведенные в таблице, показывают, что нелинейный гауссовский фильтр дает лучший результат по критериям (4)…(7), чем линейный гауссовский фильтр.

100           200           300           400           500           600

Рис. 4. Изображение, восстановленное на основе нелинейного гауссовского фильтра

Таким образом, нелинейный гауссовский фильтр, построенный на основе спектральной матричной нормы, может быть использован для восстановления искаженных пикселей изображений. Численные эксперименты подтверждают работоспособность данного фильтра и возможность его применения для решения практических задач цифровой обработки изображений.