Восстановление эквивалентного профиля показателя преломления оптического волокна по диаграмме дифференциальной модовой задержки

Для разработки методов контроля и отбора в процессе инсталляции инфокоммуникацион-ных сетей многомодовых оптических волокон (МОВ) по критериям согласования с лазерными источниками оптического излучения представляет интерес задача восстановления эквивалентного профиля показателя преломления МОВ по результатам измерений диаграммы дифференциальной модовой задержки – DMD (differential mode delay), инсталлируемой линии передачи. Форма и параметры эквивалентного профиля могут существенно отличаться от профиля показателя преломления измеряемого волокна. Важно, чтобы эквивалентный профиль обеспечивал приемлемую точность расчета диаграмм DMD в рабочем диапазоне длин волн при возможных вариациях условий ввода. Такой подход базируется на основах теории эквивалентных оптических волноводов и принципах моделирования эквивалентного профиля показателя преломления, заложенных в работах [1-4].

Фактически рассматриваемая задача сводится к синтезу эквивалентного профиля показателя преломления МОВ. В общем случае используемые для этих целей методы анализа должны быть универсальными и обеспечивать необходимые точность и быстродействие. При этом одной из основных проблем анализа МОВ является исключение фиктивных решений, не имеющих физического смысла. Это во многом и определило широкое распространение метода приближения Гаусса [2-4], позволяющего вычислять отдельно параметры каждой моды. Его применение представляет интерес и для решения поставленной задачи, поскольку синтез должен быть выполнен в процессе контроля МОВ при инсталляции линии, что требует увеличения быстродействия и, как следствие, вынуждает ограничить точность, используя приближенные методы. В работах [5-6] описан синтез профиля показателя преломления на основе универсального метода расчета параметров мод, базирующегося на совместном использовании метода приближения Гаусса и метода стратификации. Вместе с тем задача синтеза эквивалентного профиля показателя преломления МОВ не предъявляет высоких требований к универсальности метода. Дело в том, что применяемые на инфокоммуникацион-ных сетях МОВ в идеале должны иметь параболический профиль. Профиль показателя преломления образцов волокон в той или иной мере является приближением к параболическому. А выпускаемые промышленностью в последние годы МОВ категорий ОМ3 и ОМ4 приближаются к нему с достаточно высокой точностью. Это позволяет увеличить быстродействие за счет ограничения универсальности метода. В частности, естественно предположить, что для описания эквивалентного профиля, учитывающего отличия профилей МОВ от идеального параболического и близкого к нему по форме, может быть использована модель, для которой существуют приближенные аналитические решения на основе метода приближения Гаусса. В работе предложен базирующийся на данном подходе алгоритм восстановления эквивалентного профиля показателя преломления МОВ по диаграмме DMD и представлены результаты его апробации на примере образца МОВ, для которого были получены данные измерений профиля показателя преломления.

Аналитические решения для частных случаев профиля показателя преломления МОВ

Метод приближения Гаусса подробно описан [4]. В [7] представлены уравнение эквивалентного радиуса пятна моды и выражения для постоянной распространения и ее первой производной в общем виде для произвольного профиля показателя преломления:

fA-n^^fcy’U)]2^— i_____________________a Ro (2)

(m + Z — l)i/(m — 1)!

8^^ _ o^JW ^VJJ ^J (3) 8k        (m + l -ty/(m -1)!

где R = r/a – нормированный радиус; r – координата; a – радиус сердцевины волоконного све- товода; R0=r0/a – нормированный радиус пятна моды; r0 – радиус пятна моды; C – константа для заданного порядка моды l, m:

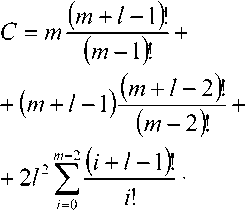
Для аппроксимации профиля на основе метода стратификации [5]:

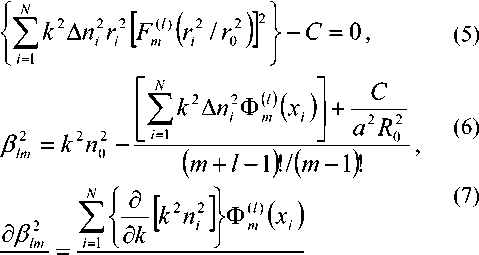
6k (m + /-l)/(m-l)!

где At?² = Hq —n^ .

А также были получены выражения для частных случаев профиля показателя преломления. Для ограниченного параболического профиля [5]:

, Ш-^У »t?q(1-2A) , l

A = k -исИ2ио)’

пйЛс – показатель преломления на оси ОВ и оболочки ОВ, соответственно, аЧг^Кл0 [(^’,+1)(0Д)- G,^0^

-с = о

+ k-W-R;. [g*^//+1)(0,1)- G^^m\R-² ,1)]} ^Ik-Vn^-

8k 0

^^^^"^"(о.О-б;,'''*^^;2,!)]

(ти + / - l)!/(m -1)!

(H)

Здесь функция С^х.Ц определяется как

In

G^ кхД= ехр(-йх) •   g^ • —— +

/g (g + А)! и (q + р - к).

хч+А'”к ~Ь^

Для профиля показателя преломления, описы ваемого функцией Гаусса [5]:

и² (R) = Ир + (и„ - и| )ехр(- R² / Rq ), (13)

п₀,п_с – показатель преломления в центре сердцевины ОВ и оболочки ОВ, соответственно; R_G – безразмерный параметр;

С - crk^n'R^p ■ с'^л/+1)(о,/)) - 0, (14)

k^n-R-G\*-l\O,b^-- а

(m + / - 1)/(т -1)!

, =8^+*M_RX^L,16)

ск дк (т + /-1)!/(т-1)!

Здесь p-R^R^b-\^p.

Модель профиля показателя преломления МОВ

Статистические исследования профилей показателя преломления образцов МОВ выявили следующие характерные отличия их от идеального ограниченного параболического профиля [8,9]. Это – провал или пик по оси волокна, сглаженный переход на границе сердцевина-оболочка и отклонение формы профиля от параболы в средней зоне. В [9] рассмотрена кусочно-степенная аппроксимация профиля. Однако для такого профиля при произвольных значениях показателя степени не кратных двум метод приближения Гаусса не позволяет получить аналитические решения. В данной работе предлагается описание профиля показателя преломления суммой элементарных функций, для которых методом приближения Гаусса уравнение эквивалентного пятна моды, выражения для постоянной распространения и ее первой производной получены в аналитическом виде. В частности, суммой ограниченной гауссовской функции и ограниченной полиномиальной функции:

n-(R)=\ ^{р GA}, ,               '     (I?)

n_G, 1 <  R < оо ;

ⁿGA =к -и^ ехр(-Л² /R;Y

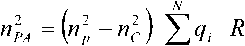
/=i гдепр’ ng'Rg% b.– параметры профиля.

На рис.1 и рис.2 приведены данные измерений профиля показателя преломления для двух типичных образцов МОВ и результаты их аппроксимации согласно (17) при N = 4. Для определения параметров использовали метод наименьших квадратов. Как видим, эквивалентный профиль, определяемый согласно (17), достаточно хорошо согласуется с данными измерений уже при 7V = 4 .

1.4566

1.4565

1.4565

1.4564

1.4564

1.4563

данные измерений — аппроксимация

О 5     10    15    20    25    30

радиус, йкм

Рис. 1. Пример аппроксимации профиля показателя преломления образца МОВ

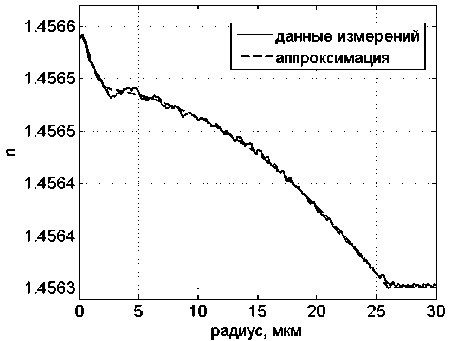
Рис. 2. Аппроксимация профиля показателя преломления образца МОВ

Аналитическое решение для модели эквивалентного профиля показателя преломления

Подставляя (17) в (1)-(3), с учетом (8)-(16) получаем уравнение эквивалентного пятна моды в виде:

С -С -С = о, РА '"GA ^{v и} ’

С„ =a’-k’-^;-n^RPs,

S = f И '"'(ОД)" Ор^пК^! ,1]- Л" • _?,, <>») Z=1

д™=к'*"(о.б)-бУ'*4^

Выражения для постоянной распространения и ее первой производной принимают вид:

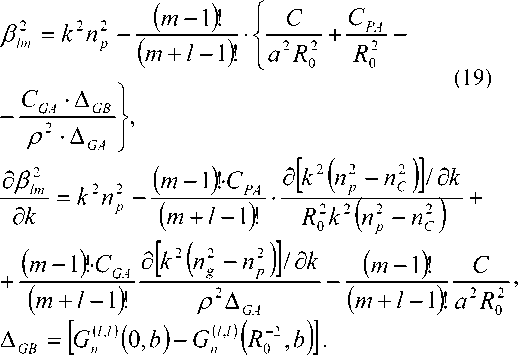
Групповая задержка моды, соответственно,

1    ^Plm равна t]m =-- , где с – скорость света.

^-Plm^C 8k

Диаграмму DMD будем рассчитывать по формуле

^_lm ~ ^im -^miⁿ(^z/,„).           (20)

Таким образом, задавая эквивалентный профиль показателя преломления МОВ формулой (17), можно рассчитать диаграмму DMD, используя аналитические выражения (18)-(20) или воспользовавшись выражениями (5)-(7) и (20).

Алгоритм восстановления эквивалентного профиля показателя преломления

МОВ по диаграмме DMD

Поскольку эквивалентный профиль МОВ описывается согласно (17), можно полагать, что он будет полностью восстановлен при нахождении параметров a, n_p, n_g, n_c, R_g и q_r В подавляющем большинстве случаев оболочка изготовлена из чистого кварцевого стекла и параметр n_c можно считать известным. Как было отмечено выше, приемлемую погрешность аппроксимации профиля МОВ эквивалентным достигаем уже при N=4. В этом случае число неизвестных не превышает 8, и для их поиска можно воспользоваться методом Нелдера-Мида [10]. Целевую функцию запишем следующим образом:

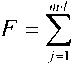
|^’-Д^?/Д^'Ч

Im          Im J Im ^.

В качестве начального приближения задаем идеальный ограниченный параболический профиль.

Апробация алгоритма восстановления эквивалентного профиля показателя преломления МОВ по диаграмме DMD

В целях апробации предложенного алгоритма восстановления эквивалентного профиля показателя преломления МОВ по диаграмме DMD были выполнены расчеты для примера профиля показателя образца МОВ. Данные измерений на длине волны 650 нм профиля показателя преломления образца волокна были представлены двумя массивами значений показателя преломления и радиуса, соответственно, размерностью 1×264 каждый. Пересчет значений показателя преломления на другую длину волны выполнялся по формуле Селлмейера по методике, подробно описанной в [11]. Исследуемый профиль на длине волны 1300 нм приведен на рис.3. Предварительно методом смешанных конечных элементов [12, 13] по данным измерений профиля были рассчитаны диаграммы DMD на длине волны 850 нм и 1300 нм. Затем, используя предложенный алгоритм, по диаграмме DMD, рассчитанной на длине волны 1300 нм, был восстановлен эквивалентный профиль показателя преломления (рис.3). Были получены следующие параметры эквивалентного профиля на длине волны 1300 нм a- 28,26 мкм; и_;,= 1,45985; n_g= 1,44963; R_g -0,06; ^=1,14; q, =0,25; q₃ =-0,06; q₄ =-0,42.

Для полученного эквивалентного профиля по предложенной в данной работе методике были рассчитаны диаграммы DMD на длине волны 850 нм и 1300 нм. Результаты вычислений приведены на рис. 4-5.

Как видим, диаграммы DMD, рассчитанные по эквивалентному профилю, достаточно хорошо согласуются с диаграммами, полученными для оригинального профиля образца ОВ. Как и следовало ожидать, погрешности на длине волны, на которой эквивалентный профиль был восстановлен (1300 нм), сущест- венно меньше.

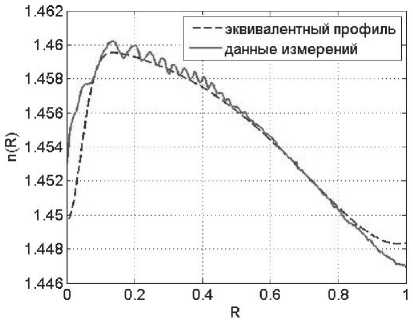
Рис.3 Оригинальный профиль образца МОВ и восстановленный для него эквивалентный профиль показателя преломления

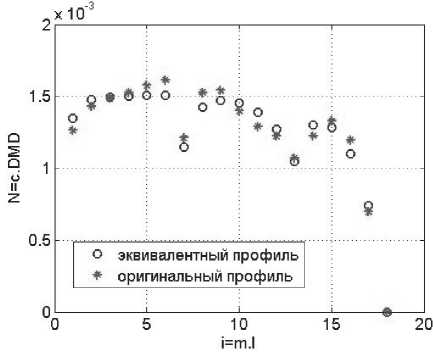
Рис.4 Диаграммы нормированной дифференциальной модовой задержки на длине волны 1300 нм (^ -lp_Q6 для i = 1 - 6 ; LP_n -LP_X6 для i = 7 - 12 ; LP_1X — LP₂₆ для i = 13 - 18 )

„х10"

1--------

0.8

Q

0.6

о °

о

о

о

Q

0.4 - о

0.2-

°0

*

о

о эквивалентный профиль

* оригинальный профиль

О

о

О о

О

*

о

*

—1-----е---'

10         15

i=m.l

° о

Рис.5 Диаграммы нормированной дифференциальной модовой задержки на длине волны 850 нм ( ^oi LP₀₆ для i = 1 - 6 ; LP_XX-LP_X6 для i = 7-12 ;

LP„ -LP₆ для i = 13-18 )

Полученные результаты позволяют говорить о возможности применения предложенного способа восстановления эквивалентного профиля показателя преломления МОВ в задачах контроля DMD МОВ при инсталляции линий передачи. Однако, чтобы рекомендовать его для этой цели, необходимо проведение исследований зависимостей от рассогласований при вводе оптического излучения в волокно.