Восстановление линейно смешанных сигналов на основе адаптивного алгоритма рекуррентной сети

ВВЕДЕНИЕ                    и построен алгоритм для НС простой структуры.

Однако работа этого алгоритма не обладает устой-

В ряде специализированных информационноизмерительных систем (ИИС) (например, радарного зондирования и мониторинга, медикобиологических комплексах), при адаптивном выравнивании усиления и адаптивном снижении шумов в каналах связи, для усиления сигналов многоканальных датчиков, при анализе негауссовых массивов данных, обработке цветных изображений, в отдельных задачах радиационного контроля требуются элементы идентификации первичной совокупности сигналов, регистрируемых только в линейно смешанном виде [1-5]. Как правило, в этих приложениях бывают неизвестными и вид сигналов источника, и количественные пропорции их смеси в регистрируемых сигналах. При квазистационарности и независимости первичных сигналов возможно их восстановление. Ввиду отсутствия информации о составе исходных сигналов и структуре их смешанного воздействия на датчики ИИС реконструкция принципиально не может быть полной. Она восстанавливает форму действующих сигналов, оставляя в качестве неопределенности порядок компонент входного век-тор-сигнала (совокупности первичных сигналов) и их масштаб, т. е. сигналы восстанавливаются с точностью до обобщенной перестановки [6, 7].

Восстановление формы сигналов может осуществляться на основе нейросетевого (НС) алгоритма, начальное формирование которого выполнено Комоном, Джутен и Херолдом [8, 9]. Ими намечен общий подход к решению задачи восстановления чивостью, сопровождается нарушением при значительной неравномерности масштаба отдельных сигналов и/или при плохой обусловленности матрицы смешивания, а также имеет временные срывы даже в благоприятных ситуациях относительно объективных характеристик, которые могут осложнять решение задачи.

Ниже представлен детальный анализ методической схемы из [8, 9] и даны две модификации алгоритма, одна из которых ориентирована на НС с прямым распространением сигнала, а другая — на рекуррентную НС (с обратными связями). Первый вариант алгоритма (частично) и второй (полностью) лишены упомянутых недостатков: они практически независимы от большой неравномерности масштабов восстанавливаемых сигналов и от степени сингулярности матрицы смешивания.

ЗАДАЧА ВОССТАНОВЛЕНИЯ СМЕШАННЫХ СИГНАЛОВ И ОСНОВЫ МЕТОДА РЕШЕНИЯ

Считается, что неизвестные сигналы S j ( t ), j = 1, ..., n , имеющие различные математические и физические модели, совместно воздействуя на датчики ИИС, порождают на их выходах измеряемые (системой) сигналы x 1, ..., x_n , которые представляют некоторую линейную комбинацию (для каждого датчика свою) первичных сигналов s j ( t ):

x i ⁽ t ) = S П = 1 a ij ⁽ t ) s j ⁽ t ),

или

Х ( t ) = A • S ( t ),                       (1)

n       n×n n где aij (i,j = 1, ...,n) — коэффициенты линейных комбинаций; второе соотношение является векторно-матричной формой первого; А — фиксированная или медленно меняющаяся матрица с определителем      det A * 0;      s(t) = [s 1(t),...,sn(t)]T;

x ( t ) = [ x 1 ( t ),..., x_n ( t )] ^T ; размерности переменных указаны под формулой, и для простоты приняты одинаковые размерности сигналов s и x ; А называется матрицей смешивания, и она неизвестна.

Восстановление состоит в получении сигналов y 1 ( t ),..., y_n ( t ), или вектора у ( t ) = [ y i ( t ),..., y „ ( t )] ^T , который в определенном смысле аппроксимирует сигнал s ( t ). Остаточная неполнота в решении задачи состоит в неопределенности масштабирования у ( t ) и порядка его компонент { y j ( t )}, в котором система оценивает { s i ( t )}. Эта неопределенность может быть выражена соотношением [10]:

~

y ⁽ t ) = D • P • ^{s (} t ) = P • ^{s (} t ) ,        (2)

n       n×n n×n n n×n n где D — диагональная масштабирующая матрица; Р — матрица перестановок1); P — обобщенная матрица перестановок, объединяющая перестановку и масштабирование.

Хотя неопределенность является довольно значительным ограничением, в практических приложениях она часто несущественна, т. к. большая часть информации заключается в форме сигналов (как например, в биомедицинских системах), а не в величине и порядке компонент.

Рассмотрение метода восстановления линейно смешанных сигналов, формирования структуры НС и алгоритма ее обучения удобно начать с анализа первоначального подхода к решению этой задачи и некоторых результатов, содержащихся в работах [8, 9].

Оригинальная модель для оценки смешивающей матрицы А и вектор-сигнала s — модель Хе-ролда—Джутен (называемая далее моделью ХД) основана на соотношениях (3), которые соответствуют рекурсивной структуре простейшей однослойной НС:

n

y ⁽ t ) = x ⁽ t ) ^- У w j ⁽ t ) y j ⁽ t ), ^j * i ;

j = 1                                    ⁽³⁾

y(t) = x(t) - W(t)y(t), где второе выражение является матричновекторной формой первого соотношения, отражающего скалярное представление сигналов2); wj — синаптические веса (СВ) нейронной сети; W — матрица синаптических весов НС:

W ( t ) = { w j ( t )} _{/ J=u}, n , ( w_u = 0, V i ). n x n ’

С помощью (3) вектор-сигнал y ( t ), предназначенный для аппроксимации первичных сигналов s ( t ) = [ s i ( t ), ..., s n ( t )] ^T , определяется в виде

y ( t ) = [ I + W ( t )] ^{- 1} x ( t ), (4)

где I — единичная ( n x n )-матрица.

Функциональная схема, отражающая структуру задачи восстановления сигналов, которая использована в модели ХД и в разработанных более эффективных реализациях нейросетевых алгоритмов, показана на рис. 1, а структура выполняемого сетью алгоритма по модели ХД — на рис. 2, 3. Алгоритм обучения НС в модели ХД построен на наборе дифференциальных уравнений (5):

d w j ( t )

= П(t)f[yi(t)] g[yj(t)] для i * j, (5) dt в которых n(t)>0 — параметр скорости обучения; fy) и g(y) — нелинейные нечетные функции, в качестве которых использованы fy) = y3 (или f(y) = y2sign(y)) и g(y) = sign(y) (или g(y) = a tg(ey) при a>0 и в>0).

Для стабильной работы алгоритма (4) требуется, чтобы собственные числа матрицы W ( t ) находились (при любом t ) в единичном круге. Требование может быть выполнено, если сумма абсолютных величин каждой строки W ( t ) меньше единицы [12, 13]. Это условие в практических приложениях трудно выполнимо, что приводит к неустойчивости алгоритма. Некоторое ослабление такого недостатка происходит за счет того, что алгоритм действует в направлении минимизации выходной мощности НС, которая соответствует "подтягиванию" полюсов у [ I + W ( к )] ¹ внутрь единичного круга [8].

Получение алгоритма по модели ХД основано на минимизации функции стоимости (ФС), определенной как математическое ожидание своеобразной "мощности" сигнала y ( t ) на выходе НС:

Неизвестно

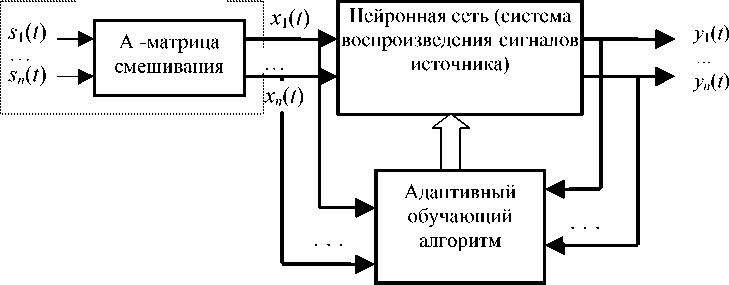
Рис. 1. Функциональная схема, отражающая структуру задачи восстановления сигналов

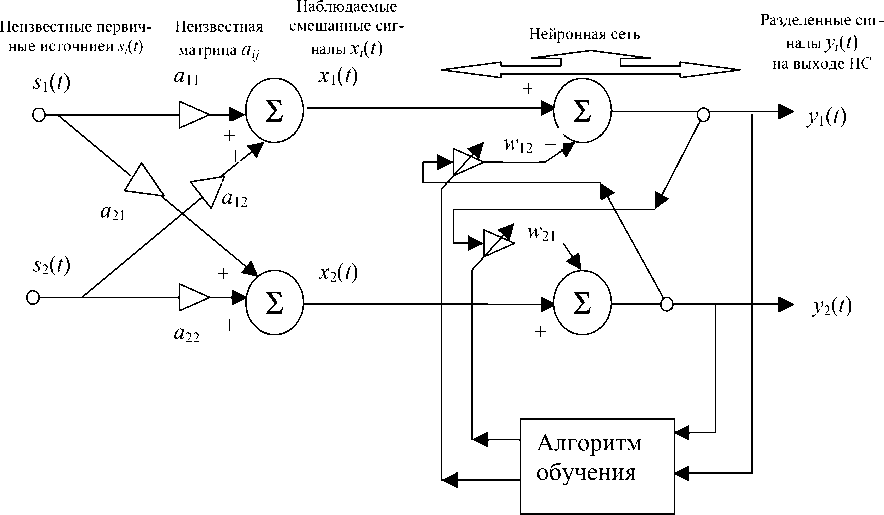
Рис. 2. Структура операций, выполняемых НС для восстановления сигналов по модели ХД при n = 2 [8]. Левая часть отражает схему формирования линейно смешанных сигналов x ₁( t ), x ₂( t )

OG( W ) = E^ P i [y . (t )] [ , . i = 1

но определяют мощность сигнала   y ( t ) =

(6) =[ y ₁( t ),..., y_n ( t )] ^T , — выражение в фигурных скобках соотношения (6):

где Е — символ математического ожидания; pi — компоненты вектор-функции р , которые аддитив-

P i ⁽У. ) = -I У. I ^Р ■ ^p

Неизвестное смешивание сигналов источника

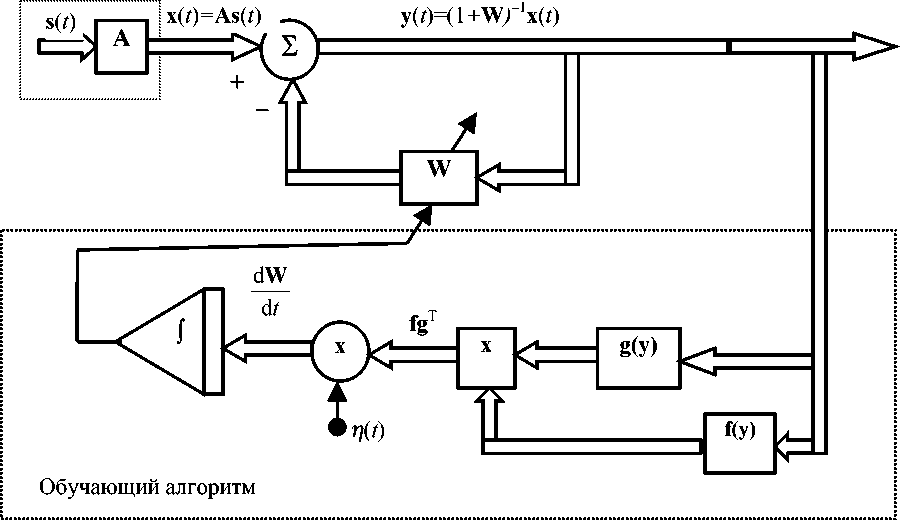
Рис. 3. Общая функциональная схема алгоритма для НС по модели ХД [11]

Для параметра р принимается значение 3, а выходной сигнал у описывается выражениями (3), (4).

Минимизация ФС осуществляется по правилу спуска вдоль антиградиента, и подстройка совокупности весов НС определяется соотношениями [14]

^d w j⁽ t )    ^дФС( W )

”^{n (} ' ) -^w-

= - n ( t ) ^{д Ф}С^{( W )} |y L = n ( t ) E{ f [ y , ( t )] y j ( t )}.   (7)

d y   d w j

Равенство первой и последней частей этих соотношений компактно представляется в векторноматричной форме (8):

(1 W                   т

-- = n ( t )E{ f [ у ( t )] у ^T ( t )},          (8)

dt где = означает эквивалентность только недиаго нальных элементов в равенстве (8); f (у) = = [f,[y 1(t)] fг[y2(t)] ....f[y„(t)]]T; f[y;(t)] = = P^L (= — равно по определению).

^d y_t

С учетом выражения для p i ( y i ) выражение для ft ^[ y , ⁽ t ^)] имеет вид: f, [ y , ( t )] = | y, | ^{p - 1}.

Поскольку математическое ожидание E{ f [ y ( t )] y ^T ( t )} неизвестно, то использована его аппроксимация ([3], [9]) в виде среднего:

E{ f [ у ( t )] у ^T ( t )} =

1 t

"T ^ f [ у ( t )] у ^T ( t )    при (9)

^T t = 1

у ( t ) = [ I + W ( t )] ^{- 1} x ( t ), t = 1,2...

Соотношение (9) не рассчитано на непосредственное использование его в реальном масштабе времени, поэтому для оптимизации в режиме online и получения решения применен метод стохастического градиентного спуска, в котором использована замена истинного градиента на его достаточно неточную "мгновенную" оценку:

E{ f [ У ( t )] У T ( t )} = f [ У ( t )] У T ( t ). (10)

Для изменения матрицы W ( t ) (подстройки синаптических весов в процессе обучения НС) с учетом (8) это приводит к выражению (11):

dW t

— = n ( t ) f [ y ( t )] y T ( t ). (11) d t

Обучающий алгоритм (10), (11) может интерпретироваться как обобщенное анти-Хеббановское правило [15–17].

Хотя алгоритм по модели ХД (до известной степени) не требует единственно возможного определения формы активационных функций f , g и полезен в отдельных приложениях, он имеет ряд существенных недостатков. Работа алгоритма нарушается, если приходится разделять сигналы значительно различающегося масштаба ("плохо масштабированные") или если матрица А является плохо обусловленной ³⁾ . Кроме того, алгоритм имеет недостаточную устойчивость, которая проявляется или непосредственно, или через некоторое время после устойчивой работы. При этом устойчивость зависит от нескольких факторов: от начальных условий, коэффициентов смешивания А и типа активационных функций. К тому же часто встречает трудности обращение матрицы для получения оценки W ( k ) = [ I + W ( k )] ^{- 1} на каждом шаге k итерации.

Анализ подхода, связанного с получением алгоритма модели ХД, служит основой для построения более совершенного метода решения задачи восстановления смешанных сигналов с использованием нейронной сети. Этот метод изложен в следующем разделе и Приложении. Он использует две модификации НС и расширение алгоритма модели ХД, которое резко улучшает качество и надежность функционирования. Предложены две структуры НС (НС прямого распространения и динамическая НС с рекуррентной структурой) и алгоритмы адаптивного обучения в несуперви-зорном (без учителя) режиме, которые практически свободны от недостатков алгоритма модели ХД.

РОБАСТНЫЙ САМОНОРМАЛИЗУЮЩИЙСЯ АДАПТИВНЫЙ АЛГОРИТМ ОБУЧЕНИЯ

НС прямого распространения

Однослойная НС простой структуры с распространением (сигнала) вперед и с линейными нейронами описывается соотношениями (12), второе из которых дано в векторно-матричной форме:

yA.t ) = ^Lw j (t ) X j (t ),      i = 1,2,-, n ;

j = 1                                            ⁽¹²⁾

~

y ⁽ t ) = W x ⁽ t ),

~ где W(t) = {wij(t)} ij; x(t) =[x 1(t) x2(t).... xn(t)] — n x n вектор сигналов, регистрируемых датчиками (сенсорами); y(t) = [y,(t) y2(t) ....y„(t)]T— вектор выходных сигналов.

После стадии обучения НС (когда синаптические веса (СВ) достигают желаемой точки равновесия) набор выходных сигналов y i ( t ) ( i = 1,2,…, n ) должен быть пропорционален первичным сигналам источника s j ( t ) ( j = 1,2,…, n ). При этом возможно несовпадение последовательности индексов сопоставляемых сигналов.

Для получения такого соответствия вектор-сигнала s(t) источника и выходного вектор-сигна-ла y(t) = [y 1(t) y2(t) ....yn(t)]T (после возможной перестановки порядка его компонент) необходимо, чтобы в точке равновесия синаптических весов W обученной сети выполнялось соотношение y (t) = W( t )x( t) = W( t) A s( t) = DP s( t), (13) т. е. чтобы полученные сигналы отличались от исходных s(t) не более чем на матрицу перестановок Р и изменение масштаба, осуществляемого некоторой диагональной матрицей D.

Это означает, что условием успешного решения задачи разделения сигналов (любого вида s ( t )) является выполнение соотношения (14), которое определяется последним равенством из (13):

W = DPA ^{- 1} .               (14)

Для описанной модели оказывается возможным применение адаптивного алгоритма обучения НС, который выражается соотношением (15) и доступен к реализации в режиме реального времени ⁴⁾ :

ˆ dW^t) = n( t ){л - f [y( t)] g T[y( t )]}\V( t),    (15)

где п (t )>0 — параметр скорости обучения; Л — диагональная матрица со значениями элементов: X X 2 , ..., X n ( X >0 V j ).

При этом для инициализации приведенного алгоритма следует использовать начальные значения синаптических весов НС с естественным условием det W (0) * 0 ; W (0) * 0 . Достаточно взять, например,

W (0) = I и такое же значение для Л ( Л = I ). Полная логика построения алгоритма дана в Приложении.

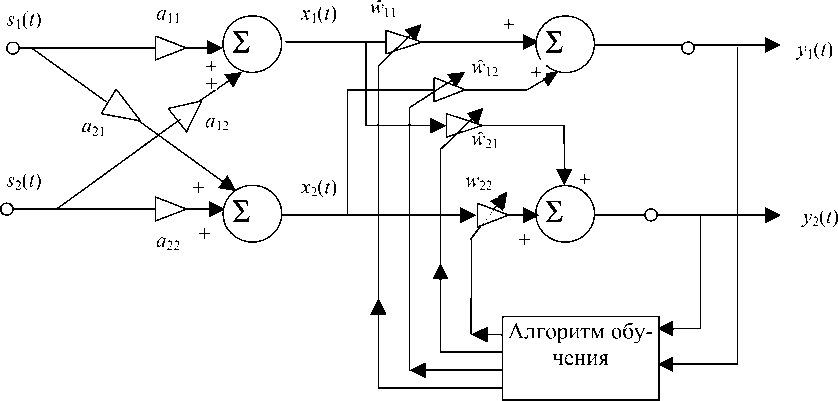
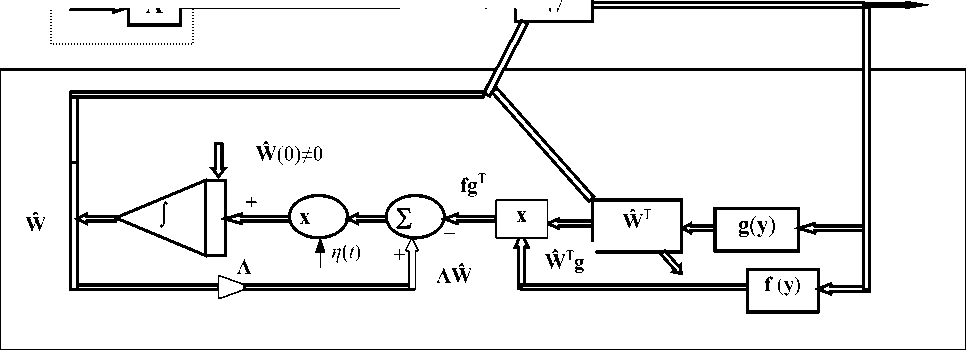
Функциональная схема алгоритма обучения при реализации его на основе использования микросхем аналоговых цепей показана на рис. 4. Алгоритм в скалярной форме представляется соотношением

a

y ⁽ t )= Wx ⁽ t )

x ( t )= As ( t )

s ⁽ t )

Ŵ

А

б

Рис. 4. Смешивание и разделение сигналов источника с использованием НС прямого распространения (сигналов).

а — подробная модель для случая двух сигналов ( n = 2).

б — функциональная блок-схема выполнения адаптивного алгоритма обучения (алгоритм определяется соотношениями (15), (16))

^{- w} ij d t

= П ⁽ t ) ^^W y

n

- ^{f [} У i ⁽ t ^)] ^ ^w pj ⁽ t ) g p [ y p ⁽ t ^)] p = 1

(i, j = 1,2,..., n ).

На первой фазе обучения (при поиске) п может быть фиксированным, а затем на второй фазе (сходимость) эту величину целесообразно постепенно уменьшать по экспоненциальному закону.

Предложенный алгоритм обучения (15) и (16) несколько сложнее, чем алгоритм ХД, но он значительно мощнее и функционирует эффективнее.

Адаптация алгоритма к компьютерной реализации осуществляется с помощью его представления в дискретной форме ⁵) :

W ( к + 1) =

= W( к) + п( к ){л - f [y( к)] g T[y( к )]}W( к); (17) k = 0 ,1, 2..., где W(0) ^ 0 и подразумевается выбор некоторой малой величины Т шага дискретизации времени. Для устойчивой работы алгоритма следует брать очень малое значение параметра п [16], [17].

Усовершенствованный алгоритм, который отражается соотношениями (15) и (17), достигает точки равновесия, когда выполняются два условия (18а, 18б):

• 1)    Е{ ^{f [} y i ⁽ t ^)] g j ^[ y j ⁽ t ^)]} = ⁰ при i * ^j . ^(18а) 2) Л -= E{ f[y_t)]gi[У,(t)]} = 0 при i = j. (18б)

Метод, использованный при получении алгоритма (15) и (17), (при некотором сходстве с формированием алгоритма по модели ХД, например по функциям активации f ( y ) и g ( y )) отличается по структуре НС и правилу обучения, обладает высокой устойчивостью и независимостью от выбора начальных условий. Кроме того, усовершенствованный подход к решению задачи восстановления сигналов имеет ряд положительных свойств:

• •    Рассматриваемая схема алгоритма построена на сети с прямым распространением сигнала

  f ( к + 1) - f ( к ) ( к + 1) - к

  
  

  = f ( к + 1) - f ( к ) .

  
  

( У = Wx ); она не требует обращения матрицы на каждом временном шаге (как это необходимо в соотношении (4) для выполнения алгоритма по модели ХД).

• •    Процедура выполнения алгоритма обеспечивает самоорганизующуюся нормализацию величины (строго говоря, энергии) выходного сигнала y ( t ). Иначе говоря, алгоритм обладает свойством адаптивного управления усилением в нейронной сети за счет самостоятельной подстройки синаптических весов w ii .

• •    С помощью процедур, реализуемых алгоритмом, возможно разделение сигналов источника с очень большим диапазоном величины (их энергии). Плохая обусловленность матрицы смешивания А (которая может быть связана с почти полной идентичностью передаточных функций измерительных датчиков) не затрудняет корректную работу алгоритма.

Отмеченные преимущества метода, положенного в основу анализируемого алгоритма, проявились при его компьютерном моделировании.

Можно обратить внимание на некоторые дополнительные соображения. Строго говоря, общее функционирование алгоритма (15-17) происходит независимо от фактора (взаимного) шкалирования сигналов, компонент вектора s ( t ) и от показателя обусловленности смешивающей матрицы А . Это становится видно, если выполнить правое умножение соотношения (15) на матрицу А , что дает соотношение

• - р , .

• = п { л - f [ P ( t ) s ( t )] g ^T [ P ( t ) s ( t )] } ~( t ), d t

где ^р( t ) = W ( t ) A и P ( t ) может интерпретироваться как матрица, определяющая выполнение обучающего правила.

Приведенное матричное дифференциальное уравнение описывает динамическое поведение общей системы смешивания и разделения (восстановления с точностью до обобщенной перестановки) сигналов, которое не зависит от параметров смешивания и масштабирования (т.е. от вида матрицы А ).

Следует отметить, что полное теоретическое обоснование сходимости матрицы ^р( t ) к обобщенной матрице перестановок пока отсутствует. Имеется лишь достаточно обширная эмпирическая база, полученная компьютерным моделированием и подтверждающая эту сходимость. Тем не менее остается не вполне решенным вопрос, каким условиям и ограничениям должна удовлетворять матрица G ( y ) в обобщенном правиле обучения

ZX dW

-- = n(t) G[y(t)] W(t), dt для того чтобы быть уверенным в такой сходимости.

Аналогично, нерешенной остается задача формализованного подхода к такому способу выбора активационных функций fi(yi) и gj(yj) в (15–17), чтобы они обеспечивали наиболее быструю сходимость к решению задачи восстановления сигналов источника. Однако компьютерным моделированием удается установить, что из всех видов нечетных активационных функций, которые могут быть выбраны в алгоритме (15–17), наиболее благоприятны для разделения сигналов функции вида fi[y.(t)] = yip signy .);

g j ( y j ) = tgh(10 y , ); V г , j = 1,..., n ; p = 1,...,5.

Хорошие результаты получаются с этими функциями для сигналов, имеющих уплощенное (относительно гауссова) распределение, т. е распределение с отрицательным эксцессом. Напротив для сигналов с положительным эксцессом распределения лучшие результаты получаются, если функции f и g поменять местами. ⁶⁾

Следует сказать, что эти выводы имеют скорее эвристическую основу, хотя и подтвержденную моделированием. Поэтому строго говоря, нельзя утверждать, что такой выбор функций возбуждения в НС безусловно оптимален или что он обеспечивает сходимость для любой формы распределения сигналов источника.

Нейронные сети с обратными связями (рекуррентные НС)

НС прямого распространения проста, легко выполнима программно или схемно (на основе интегральной технологии), темпорально устойчива и независима от начальных условий. Но иногда (хотя значительно реже, чем у алгоритма ХД) особенности разделяемых сигналов создают трудности решения задачи восстановления формы сигналов (ВФС), особенно при значительном различии масштабов сигналов или резко выраженной степени сингулярности ⁷⁾ смешивающей матрицы А .

В приложениях, характеризуемых такими осложняющими элементами, синаптические веса НС могут принимать большие значения, а работа алгоритма — становиться неустойчивой. При аналоговой реализации нейросетевого алгоритма этот недостаток особенно неудобен, т. к. вызывает эффект насыщения в интегральных элементах электроники.

Более совершенная организация алгоритма для решения задач ВФС основана на применении НС, структура которой использует принцип обратной связи. Функционирование такой сети, называемой рекуррентной нейронной сетью (РНС) [17], в терминах вход—выход ( x → y ) описывается в развернутой (покомпонентной) форме соотношением (19а) и в векторно матричной форме — соотношением (19б):

n у.(t)=xi(t)-Xwij(t)y/t); i=i2’-’n. (19а) j=1

y ( t ) = x ( t ) - W ( t ) y ( t ).             (196)

Выход РНС y(t) может быть определен по (19б) в виде y (t) = [I + W( t )]-1 x( t).              (20)

Анализируемая РНС является полностью рекуррентной в том смысле, что, кроме простых (контуров) обратных связей, она за счет w ii ^ 0 ( i = 1,…, n) содержит обратную связь, обращенную на входы. После обучения РНС удовлетворяет матричному соотношению (21), а преобразование последнего равенства в (21) позволяет получить выражение для матрицы W весов РНС в форме выражения (22) или (что эквивалентно) в виде (23):

y ( t ) = [ I + W ( t )] ^{- 1} x ( t ) =

= [ I + W ( t )] ^{- 1} As = DPs ( t );

W = AP ^{- 1} D ^{- 1} - 1 ;

A = (I + W)DP .

Построение алгоритма обучения РНС основано на преобразовании соотношений (15–17) (использованных выше для обучения НС прямого распространения) в соответствии со следующей логикой.

• • Выражение (15) представляется в форме (24):

личин собственных значений матрицы достигает очень больших значений. Это эквивалентно плохой обусловленности матрицы, например, когда для собственных чисел Д- матрицы А выполняется неравенство

^ min / ^Д тах

<< 1 .

л

- W ( t ^)dWF w ^{- 1 (} t ) "

d w ,

—j = - n ( t ) x d t

= - n ( t ) W ^{- 1} ( t ) { Л - f [ y ( t )] g ^T [ y ( t )]}. (24)

• Вводится обозначение (25) для матриц XW( t ) и W синаптических весов двух анализируемых типов НС (НС с прямым распространением и РНС соответственно):

W - [ I + W ( t )] ^{- 1} .               (25)

• При обычном предположении, что det(\ W ) * 0 (т. е. матрица XW ( t ) при любом значении t обратима и существует W ^{- 1} ( t )), на основании (25) W ^{- 1} ( t ) представляется выражением (26):

W ' ( t ) = I + W ( t ).              (26)

• Используется соотношение (27), являющееся следствием правила дифференцирования матричного произведения ⁸) :

- W - 1 ( t )— W - 1 ( t ) = d W - l ( t ) = d W t ) d t               d t        d t

• Путем подстановки (27) в левую часть (24) получается соотношение (28), выражающее процедуры адаптивного алгоритма рекуррентной сети для задачи ВФС:

d W t ) = - n ( t )[ I + W ( t )] { Л - f [ y ( t )] g ^T [ y ( t )]}, d t

где W (0) * I и в качестве начального условия может использоваться W (0) = 0 ( 0 — нулевая ( n х n )-матрица).

• Скалярная форма этого алгоритма определяется соотношениями (29а) и (29б), которые эквивалентны (28):

8) Правило дифференцирования матричного соотношения аналогично обычному, однако требует сохранения порядка следования матриц-множителей. Так, поскольку единичная матрица I постоянная и справедливо со-1г л1г-11 пл1г отношение W(t) W '(1) = I, то d[W W ] = dW W- + d t        dt

₊ W d W - = d I = ₀. d t       d t

n

x ^ w ij^{( t} ) - ^fi ^[ y ^{( t} ’k X w p ^{( t} ) f p ^[ У р ^{( t )]} g j ^[ у , ^{( t )]},    ^(29а)

V

p = 1

(i * j ;    i , j = 1,2,...n );

d w-

17 = ^{- n (} t )^x

r

n

^x Л ⁽ W ⁽ t ) ^{- 1) -} f i ^[ y ⁽ t H¹ X w p ⁽ t ) f p I У р ^{(t )] x}

V

р = 1

^x g ^[ y^(t >1;      ( i = ^j ; i = ¹.2.-, n ),

(29б)

где n >  0, X i >  0 и можно использовать алгоритм с X i = 0 при V i .

Функциональная блок-схема для алгоритма обучения РНС с использованием соотношения (28) показана на рис. 5.

Описанный адаптивный алгоритм обучения, представленный на этом рисунке и соотношением (28), с помощью обычной процедуры разностной аппроксимации производной может быть приведен к дискретной форме:

W ( к + 1) = W ( k ) - n ( k )[ I + W ( k )] x x { Л - f [ y ( к )] g ^T [ y ( к )]}.

В этом случае алгоритм должен быть правильно инициирован: наиболее просто выбрать начальные условия нулевыми ( W (0) = 0 ). Как бывает обычно, устойчивая работа алгоритма обеспечивается при достаточно малом значении параметра скорости обучения n ( к )• После начальной фазы обучения величину n ( к ) полезно дополнительно уменьшать, используя зависимость от времени, близкую к экспоненциальной при небольшом коэффициенте релаксации (показателе временной зависимости у экспоненты). Эти особенности настройки алгоритма зависят от временного масштаба решаемой задачи ВФС, приемлемого для нее шага дискретизации времени и интервала стационарности (квазистационарности) сигналов источника. Последнее свойство анализируемых сигналов относится к основным исходным положениям формирования анализируемого алгоритма.

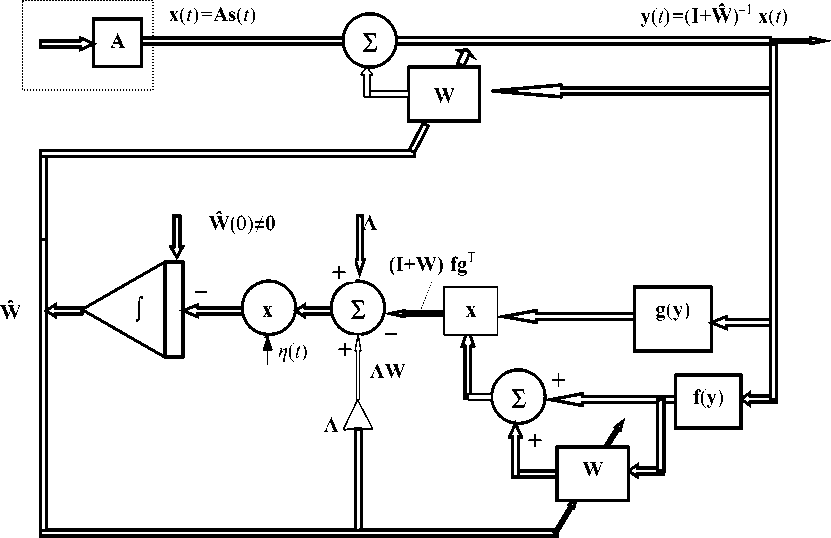
Рис. 5. Функциональная блок-схема выполнения адаптивного алгоритма обучения для рекуррентной нейронной сети (схема соответствует соотношению (28))

ЗАКЛЮЧЕНИЕ

Проведен анализ задачи восстановления группы первичных сигналов, совместное действие которых на датчики регистрирующей измерительной системы дает на выходе линейное смешивание сигналов источников. Восстановление формы исходных сигналов (сигналов источника) осуществляется на основе нейросетевого алгоритма, начальное формирование которого выполнено Ко-моном, Джутен и Херолдом [8], [9]. Условиями решения задачи восстановления является стационарность и совместная независимость первичных сигналов. Практически это означает требование выполнения этих условий на интервалах, значительно больших длительности обучения нейронной сети (НС). Из-за отсутствия априорной информации о виде первичных сигналов и пропорций их смешивания (при формировании регистрируемых сигналов на выходе измерительных датчиков) восстановление принципиально не может давать полную реконструкцию исходных сигналов. Показано, что восстановление осуществляется с точностью до масштаба сигналов и перестановки их порядка, т. е. с точностью до обобщенной матрицы перестановок (произведения канонической матрицы перестановок на диагональную матрицу).

Алгоритм из [8, 9] обладает рядом существенных недостатков: неустойчивость, временные срывы и т. п.

На основе анализа методической схемы в [6-9] введены две модификации алгоритма, одна из которых ориентирована на НС с прямым распространением сигнала, а другая на рекуррентную НС (с обратными связями). Первый вариант алгоритма (частично) и второй (полностью) лишены упомянутых недостатков: они практически независимы от большой неравномерности масштабов восстанавливаемых сигналов и от степени сингулярности матрицы смешивания.

Дана математическая форма двух модификаций алгоритмов и представление их в виде блочнофункциональных схем. Обучение НС проводится в несупервизорном режиме ("без учителя"). Алгоритм является адаптивным и несет элементы самоорганизации.

Приложение. АДАПТИВНЫЙ НЕЙРОСЕТЕВОЙ АЛГОРИТМ РАЗДЕЛЕНИЯ СИГНАЛОВ

И ВОССТАНОВЛЕНИЯ ИХ ФОРМЫ

Логика построения адаптивного нейросетевого алгоритма разделения сигналов и восстановления их формы (задача ВФС) основана на следующих предпосылках, рассуждениях и преобразованиях. Набор исходных сигналов (компоненты вектор-сигнала s ( t )) считается заданным, стационарным, некоррелированным, но неизвестным. Доступным наблюдению является вектор-сигнал x ( t ) (набор сигналов x 1 ( t ), ..., x n ( t ) — компонент этого вектора), который представляет линейное преобразование сигнала источника s ( t ) с неизвестной матрицей A . Задача ВФС состоит в получении оценки сигнала s ( t ) вектором y ( t ), который следует найти, исходя из доступных данных x ( t ), тоже на основе некоторого (пока неизвестного) линейного преобразования с некоторой матрицей W .

В соответствии с описанной постановкой задачи корреляционная матрица R_ы диагональна (П1), а x ( t ) и y ( t ) связаны линейными преобразованиями (П2) и (П3):

R„ = E [ s ( t ) s ^T ( t ) ] = D , = ( D , ) ^1/2 ( D , ) ^1/2 ; (П1)

x ( t ) = As ( t );                                (П2)

y ( t ) = Wx ( t ) = WAs ( t ).                 (П3)

Корреляционная матрица R _xx может быть факторизована в виде R _xx = VDV ^T , где D — диагональная матрица собственных значений R _xx ; V — связанная с ней матрица собственных векторов. Поэтому, чтобы убедиться, что компоненты y ( t ) тоже некоррелированы (и матрица R yy —диагональная), достаточно в соотношении

R yy = E[ y ( t ) y ^T ( t )] = E[ Wxx ^T W ^T ] = WR xx W ^T в качестве W использовать матрицу V . С учетом того, что матрица собственных векторов ортогональна (и следовательно, VV ^T = V ^T V = I ), это свидетельствует о диагональности корреляционной матрицы сигнала y ( t ):

R_w = WR W ^T = V ^T RV = yy          xx                 ss

= V ^T VDV ^T V = D = Л ,        (П4)

где Л = diag( X i ,..., X n ) — диагональная матрица.

В силу того, что нейросетевой алгоритм имеет отчетливо выраженное свойство адаптации, в качестве Л может быть принята единичная матрица I .

Автокорреляционная матрица R yy тоже может быть факторизована:

R yy = WW ^T ,             (П5)

где W = WAD * ^/2 ; D * ^/2 = R_и ^1/2 .

Чтобы сформулировать адаптивный обучающий алгоритм для итеративного обновления элементов матрицы W , достаточно сформировать следующую функцию стоимости ФС:

ФС = ¹

nn

I '.">W i=1 j=1

(П6)

где r_i j — элементы корреляционной матрицы R _yy :

rj = E[ y.(t) yj(t)];      i,j = 1Д-, n.

Эта функция стоимости может быть представлена в матричной форме:

ФС = 4||Ryy -Л||у,(П8)

где ||...|| у — норма, определяемая как сумма квадратов всех компонент матрицы (норма Фробениуса).

Правило подстройки синаптических весов НС определяется на основе минимизации ФС с использованием метода градиентного спуска, который с учетом "цепного" правила дифференцирования сложной функции дает соотношение dwtJ     ., дФС     . . Л дФС дги

—j = -n( t    = -n( t )LL^ k^, d t            д Wy           k=1 l=1 д rkl д wj

(П9)

где n ( t ) — параметр скорости обучения. При этом процедура минимизации заставляет корреляционную матрицу R yy двигаться к диагональной матрице Л = diag( X 1, ..., X n ).

Поскольку корреляционная матрица R yy сигнала y ( t ), оценивающего источник s ( t ), связана с матрицей весов W = [ w j ] n _{х x} уравнением (П10), то после некоторых преобразований получается более развернутая форма (П11) для соотношения (П9):

R yy = WW T, dwij n . дГц VVr дrki

=I '- i d t -IZ ^r »a w

n

nn

^2-i ^W y ^- I ^r ik ^W kj ^- I ^r lj w j kl

(П10)

(П11)

где X i >  0 и для практических задач ВФС можно принять X i = 1 для всех i .

Упрощение (П11) может быть получено в виде (П12) за счет использования свойства симметрии корреляционной функции (rij = rji) и последующего представления этого результата в матричной форме (П13):

d W_y d t

П A w ij

n

X ~

- L r ik w kj

k

( i , j = 1,2,..., n );

~

-- = п [ л - R yy ] W . d t

(П12)

(П13)

Умножение справа выражения (П13) на D s ^4/2A ^{- 1} дает выражение (П14), которое на основании соотношений (П5) ( W = WAD s ^1/2 ^ ^ WD s ^{- 1/2} A ^{- 1} ) естественным образом сводится к более простой векторно-матричной форме (П15):

~

• -WD , ^4/2A ^{- 1} = п [ л - R yy ] WD , ^4/2 A ^ч;    (П14)

dt dW = п[л - E(yyt)]w.          (П15)

d t

Уничтожение множителя [ Л - E( yy ^T )] может происходить, если вектор-сигнал y ( t ) имеет некоррелированные компоненты с соответствующими дисперсиями A i . В отдельном случае для Л = I аннулирование [ Л - E( yy ^T )]происходит только, если компоненты аппроксимирующего сигнала y ( t ) будут некоррелированными и иметь единичную дисперсию (т. е. их нормировка предусматривала выполнение этих свойств).

Поскольку восстановление (разделение) сигналов источника производится только с точностью до масштаба, то можно полагать, что они тоже имеют дисперсию ( o s ² ), равную единице, т. е. что корреляционная матрица R ss = I . Это связано с тем, что скалярные множители (определяющие масштаб S j ( t ), j= 1,2,..., n ) могут обмениваться между сигналами источника и столбцами матрицы смешивания А .

Для сигналов s ( t ) с o s ² = 1 корреляционная функция R yy выходного сигнала y ( t ) определяется выражением:

R_v = WAR A ^T W ^T = WA ( WA ) ^T = P P ^T ,

(П16) где P = WA .

Для этого случая алгоритм обучения (П15) для решения задачи ВФС на основе адаптивной самонастраивающейся НС может быть представлен соотношением (П17):

— = n [ l - P P ^T ] w ( t )         (П17)

dt при Л = I и P = W(t)A.

Преобразование (П17) путем умножения справа на матрицу А (не зависящую от времени) позволяет использовать еще одну эквивалентную форму (П18) или (П19) математической основы этого алгоритма:

/X

П.Р Г л а _т I /X

• -- = n [ l - P ( t ) P ^T ( t ) ] p ( t ),         (П18)

d t

/X dP 22 . . L 22 t . . 22 . . 1                  ____

• — = n P ( t ) [ i - P ^T ( t ) P ( t ) ] .          (П19)

d t

При подстройке НС равновесие в алгоритме достигается, когда правая часть в (П18) или (П19) начинает стремиться к нулю, т. е. когда матрица P ( t ) = W ( t ) A становится ортогональной матрицей, удовлетворяющей условию (П20 ):

^       ^ -p            ^ -p ^

P( t )P T( t) = PT P = I, ^   .       ^ -p или P1 = P T.

(П20)

Ортогональная матрица в общем случае не равна матрице обобщенной перестановки (перестановки с перенормировкой компонент), поэтому алгоритм (П15) и его последующие формальные модификации не дают уверенности в корректном разделении сигналов, а только гарантируют декорреляцию и нормализацию выходных сигналов — компонент вектора y ( t ). Так что условие (П20) не является достаточным для задачи ВФС, а только необходимым — для обеспечения общей независимости выходных нормализованных ( o _yi ² = 1) компонент сигнала y ( t ). Кроме того, алгоритм (П15) использует статистики второго порядка ( E( y_i y_j ) ) , производящие декоррелированные выходные сигналы. Этого недостаточно, чтобы быть уверенными в их независимости. Для достижения взаимной независимости выходных сигналов необходимо заменить линейные функции в E( y^j ) на две нелинейные различающиеся функции f(y ) и g(у ), что приведет к модификации алгоритма в форме выражения (П21):

d W = n { Л - E[ f ( y ( t )) g ^T ( y ( t )) ] } W ( t ). (П21) d t

Оправданность использования в нейросетевом алгоритме нелинейных функций f [ y ( t )] и g [ y ( t )] связана с тем, что с их помощью вводится вычисление статистических моментов более высокого порядка (сравнительно со вторыми моментами), и это уже при их нулевом (а практически при очень малом) значении обеспечивает общую независимость компонент вектор-сигнала y ( t ).

Установление полной независимости является обычно сложной задачей, потому что она требует знания плотности распределения или ее оценки.

В общем случае для этого требуется, чтобы были исчезающе малыми статистические моменты более высокого порядка или обобщенные моменты E[ f ( y_i ( t )) g ^T ( y_j ( t ))], i ≠ j . На практике величина математического ожидания (определяемого распределением вероятности) неизвестна, и она аппроксимируется своей мгновенной величиной в конце выполнения стохастического градиентного алгоритма (15) и (16).