Восстановление после препятствий лазерных пучков, содержащих угловые гармоники

Манипулирование микрообъектами с помощью лазерных пучков – весьма бурно развивающееся в последнее время направление. Впервые возможность использования лазерного излучения для манипулирования микрочастицами была продемонстрирована в 1970 [1]. При этом использовался гауссовый пучок (фундаментальная мода лазерного излучения). С тех пор, идея бесконтактного управления процессами микро- и нано- масштаба успешно реализовывается в различных областях: для торможения, отклонения, охлаждения и локализации атомов [2-5], для захвата и разделение различных типов бактерий, клеток, вирусов [6-7], для изоляции генов в хромосомах, спайки клеток удалением общей стенки при помощи «оптического скальпеля» [8-9], в нанотехнологиях и управлении элементами микромеханики [10-11].

Расширение области применения лазерных «ловушек» потребовало их усложнения с целью получения новых дополнительных возможностей. Таких возможностей можно добиться при использовании лазерных пучков, согласованных с высшими модами Бесселя, Гаусса-Лагерра, угловыми гармониками (световыми воронками) и их специальными суперпозициями. Благодаря замечательным свойствам этих пучков можно производить с микрообъектами различные действия, такие как: управлять движением потока частиц, вращать их, захватывать в пространственные «ловушки», расположенные в определённом порядке. В качестве объектов манипуляции могут быть использованы самые различные частицы – отдельные атомы, молекулы, бактерии и вирусы, мелкодисперсные взвеси и аэрозоли.

В последнее время повышенное внимание привлечено к бесселевым пучкам, обладающим такими свойствами, как инвариантность при распространении в свободном пространстве и отсутствие расходимости на интервале устойчивости, восстановление первоначальной конфигурации по прошествии некоторого расстояния при внесении в пучок объекта-препятствия [12, 13]. Эти свойства позволяют формировать длинную световую «нить», вдоль которой можно захватывать частицы одну за другой с некоторым интервалом без разрушения структуры пучка. Таким образом, бесселевы пучки удобно использовать при необходимости одновременного манипулирования набором микрочастиц [14-16]. Однако ввиду бесконечной эффективной ширины бесселевого пучка, его невозможно воспроизвести точно. В результате ограниченности размера и энергии, пройдя некоторое расстояние, сформированный пучок теряет свои замечательные свойства и «разваливается», переставая сохранять первоначальную конфигурацию. Кроме того, при изображении линзовыми оптическими системами, что часто необходимо при микроманипулировании, бесселев пучок приобретает расходимость [17].

Пучки, согласованные с модами Гаусса-Лагерра (ГЛ), как правило, не используются для множественного продольного захвата микрообъектов ввиду присущей им расходимости. Однако они не искажаются при прохождении через линзовые оптические системы, и сохраняют свою конфигурацию (с точностью до масштаба) на неограниченном расстоянии (как отдельные моды, так и их специальные суперпозиции). Кроме того, они имеют конечный эффективный радиус, а значит, могут быть весьма точно воспроизведены оптическими системами. Таким образом, возможности их восстановления после прохождения препятствий представляют определенный интерес.

Моды Бесселя и ГЛ высших порядков содержат угловые гармоники (УГ), или световые воронки [18], обеспечивающие винтовой характер фазы и наличие орбитального углового момента (ОУМ) [19]. При захвате микрочастицы в такой пучок, она получает вращательное движение. В [20] рассмотрены новые типы лазерных пучков, обладающие ОУМ, – УГ, «внедренные» в плоский или гауссовый пучок. Такие поля после прохождения некоторого расстояния, приобретают довольно устойчивую конфигурацию, напоминающую моды ГЛ, и распространяются по похожим законам. То есть, они могут быть без искажений преобразованы линзовой оптической системой, и, с точностью до масштаба, сохраняют свою конфигурацию при распространении. При этом формирование полей, согласованных с УГ, легко реализуется с помощью фазовых дифракционных оптических элементов (ДОЭ) [21].

В данной статье рассматриваются возможности восстановления различных лазерных пучков после препятствия, которым может служить захваченная этим пучком микрочастица. Проводится сравни- тельный анализ свойств восстановления мод лазерного излучения Бесселя, ГЛ и других пучков, содержащих УГ. Приведены экспериментальные результаты восстановления бесселевых пучков различных порядков.

Восстановление бесселевых пучков после препятствий

Моды Бесселя:

T (x, y,z) = iⁿ ^ 2 n sin 9 0 J_n ( k sin 9 0 r)

exp [i (n ф + kz cos 90)]

L7a ,                                     (1)

являются решением уравнения Гельмгольца и обладают бесконечной энергией (как и плоская волна). Выражение (1) ( 9 ₀ - минимальный угол отклонения конических волн) описывает скалярный непараксиальный бесселев пучок, который не претерпевает дифракции при распространении вдоль оси z и сохраняет свой диаметр.

На практике моды Бесселя формируются с помощью оптических элементов, имеющих конечный диаметр, и сохраняют модовый характер на конечном расстоянии, которое пропорционально радиусу элемента и обратно пропорционально масштабному коэффициенту функции Бесселя а = k sin 9 ₀ [22]:

z max

R _nf k ^{2   2}

----= R —ч — 1 tan ^ o ( а ² J

В оптических схемах для манипуляции микрочастицами с помощью Бесселевых пучков [14-16] сферическая линза фокусирует световую энергию в фокальной плоскости путём отображения Бесселевого пучка, созданного аксиконом или голограммой. Известно, что после отображения Бесселевого пучка сферической линзой, он теряет свойство сохранения своего диаметра и начинает расходиться (линза привносит в Бесселев пучок расходящийся волновой фронт). [17]:

^{T (} P .z) = a J o z

ksin 9n ap ]

-------⁰----I exp z )

tkpt f i + a

2 z

z

, (3)

где p ²= u ² + v ² , a - расстояние до сферической линзы.

Выражение (3) соответствует параксиальному Бесселеву пучку, созданному с помощью узкой круглой диафрагмы радиуса а в непрозрачном экране:

^T i (г. ф >^z) = ^{( - i)n + 1 а} exp i-k- ^{( r 2} ■ ^{a 2} z      2 z

f ka r ^

J_n II exp(in ф ), V z )

который, в отличие от непараксиального Бесселева пучка (1), претерпевает дифракционные изменения (расхождение) при распространении вдоль оси z.

Как было сказано выше, на практике идеальный Бесселев пучок не может быть получен ввиду конечности апертуры любой реальной оптической системы и конечной энергии любого реального источника из- лучения. Это ограничивает расстояние «устойчивости», модового поведения пучка, которое описывается формулой (2). Тем не менее, Бесселевы пучки активно используются для манипулирования микрообъектами, т.к. обладают замечательным свойством быстро восстанавливаться после искажения некоторым препятствием. При этом «тени», возникающие от препятствий, расходятся по конусу, как показано на рис. 1.

В [12], исходя из геометрических соображений, было получено выражение для протяженности тени вдоль оптической оси:

z _s

^{r 0}    , (5)

tan ^ o

где r ₀ – радиус препятствия. Выражения (2) и (5) аналогичны. Понятно, что чем больше угол 9 0 , тем быстрее будет восстанавливаться пучок. Однако расстояние «устойчивости» (2) при этом тоже будет сокращаться. Увеличить его можно увеличением размеров бесселевого пучка во входной плоскости.

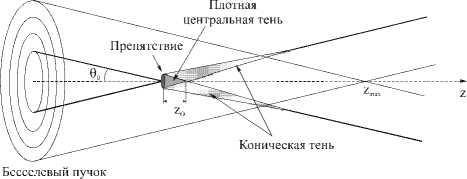
Рис. 1. Схема формирования тени при освещении Бесселевым пучком непрозрачного препятствия

Как правило, исследуются свойства восстановления моды Бесселя нулевого порядка. Ниже приведены экспериментальные результаты, позволяющие сравнить свойства восстановления мод Бесселя различных порядков (см. рис. 2, 3). Бесселевы пучки формировались с помощью фазовых ДОЭ. На некотором расстоянии после ДОЭ, центральная часть пучка закрывалась непрозрачным экраном ( r _o=0,4 мм). Затем, фиксировалось поперечное распределение интенсивности пучка на различных расстояниях от экрана. Для сравнения, на рис. 2, 3 приведены распределение интенсивности пучка, зарегистрированные без введения препятствия.

Как видно из результатов эксперимента, Бесселевы пучки обладают способностью восстанавливать свою первоначальную структуру даже при весьма значительных «повреждениях». Причем, расстояние, необходимое для восстановления Бесселевых пучков различных порядков, примерно одинаковое. Для восстановления центрального кольца Бесселя второго порядка понадобилось несколько большее расстояние, чем для восстановления центрального пика Бесселя нулевого порядка. Но это связано с большими размерами восстанавливаемой зоны. В этом случае коническая «тень» должна разойтись дальше и, соответственно, необходимо большее расстояние. Использование бесселевых пучков высших порядков позволит реализовывать не только одновременный захват микрочастиц сразу в нескольких плоскостях, но и их вращение.

A z=30 мм

A z=65 мм

A z=80 мм

A z=140 мм

Рис. 2. Восстановление Бесселевого пучка нулевого порядка: распределение интенсивности (негатив) на различных расстояниях (верхняя строка – без внесения препятствия, нижняя строка – после искажения препятствием ro=0,4 мм

A z=25 мм

A z=70 мм

A z=100 мм

A z=160 мм

Рис. 3. Восстановление Бесселевого пучка второго порядка: распределение интенсивности (негатив) на различных расстояниях (верхняя строка – без внесения препятствия, нижняя строка – после искажения препятствием ro=0,4 мм)

Восстановление пучков Гаусса-Лагерра после препятствий

Функции Гаусса-Лагерра являются модами среды с параболически изменяющимся показателем преломления и имеют вид:

где L_n^m ( x ) – обобщённый многочлен Лагерра:

n

Lm„(x) = (m + n)! £ (-1 )k k=0

k! (m + k)!(n — k)!

xk

В свободном пространстве функции ГЛ сохраняют свою структуру с точность до масштаба и рас-

^nm (r, Ф) =

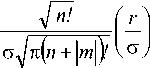
exp

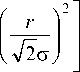
пространяются по следующему закону:

U(r, ф ,z) = exp

— ikz +

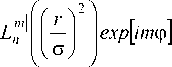
m

Ln

2 f ^r ) l ^ ( z ) J

V

exp ^[— i P nm (z) ⁺ im Ф ]

ikr ²     ( r )

-

4 R(z) ( V2 aJ

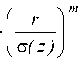
P nm (z) = ( ² n + | m | + ¹ ) ■ arctg ⁽ z/z 0 ) , (9) z 0 = ^пс 0²/ ^X , CT ² (z) = g 0 ( 1 + z 2/ z 0 ) ,

R(z) = z ( 1 + z o²/ z ² ) . (10)

где z ₀ - расстояние Релея, с₀ - эффективная ширина модовой функции в плоскости перетяжки (т.е. с ₀ = с ( z ) _z = ₀ ), X - длина волны лазерного излучения.

С помощью отдельных мод ГЛ и их линейных суперпозиций можно формировать различные конфигурации световых пучков (см. рис. 4). Индекс n является радиальным и определяет количество колец в структуре моды, индекс m – азимутальный и соответствует номеру угловой гармоники (порядку винтовой фазы).

При наличии препятствий на пути распространения моды ГЛ ведут себя по-разному. Моды с низким радиальным индексом восстанавливаются гораздо медленнее и хуже, чем моды с высоким радиальным индексом (см. рис. 5, 6). Моделирование непараксиального распространения искаженных препятствием лазерных пучков проводилось на основе разложения входного поля по сферическим волнам:

z f         exp(ikR) (1V .

F ( u , v , z ) = —         f ( x , У )---- 5I ik -— I d x d У ,

2n           R2 <

-f

R = д/(x - u)2 + (y - v)2 + z2 .(11)

При моделировании использовались следующие параметры: размер изображения 5 x 5 мм, характерный радиус ст ₀=0,39 мм, размер препятствия 0,195 мм и 0,528 мм.

(a)                               (b)

Рис. 4. Интенсивность (верхняя строка) и фаза (нижняя строка) отдельных мод ГЛ и их суперпозиций (n,m): (a) mode (0,1), (б) mode (8,–1), (в) суперпозиция мод (0,3)+(0,–3), (г) суперпозиция мод (6,4)+(6,–4)

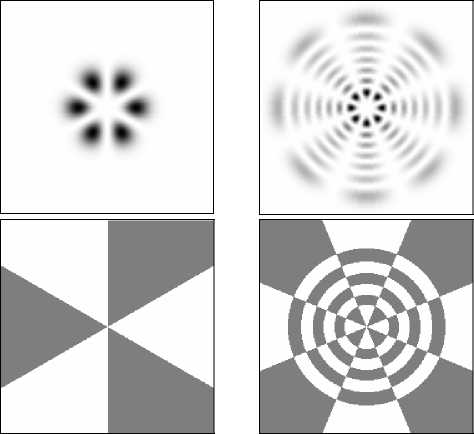
(c)                               (d)

z = 0 мм

z = 10 мм

z = 50 мм

z = 100 мм

z = 150 мм

z = 200 мм

z = 250 мм

z = 500 мм

z = 1000 мм

z = 2000 мм

Рис. 5. Восстановление моды ГЛ (n,m)=(0,1) после прохождения непрозрачного препятствия размером 0,195 мм

z = 0 мм

z = 10 мм

z = 50 мм

z = 100 мм

z = 200 мм

z = 250 мм

z = 500 мм

z = 1000 мм

Рис. 6. Восстановление моды ГЛ (n,m)=(8,–1) после прохождения непрозрачного препятствия размером 0,195 мм

z = 0 мм

z = 10 мм

z = 100 мм

z = 150 мм

z = 200 мм

z = 250 мм

z = 500 мм

z = 1000 мм

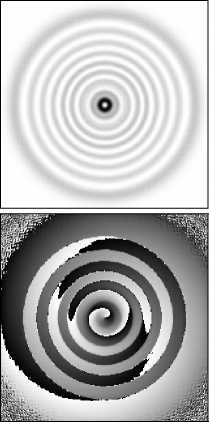
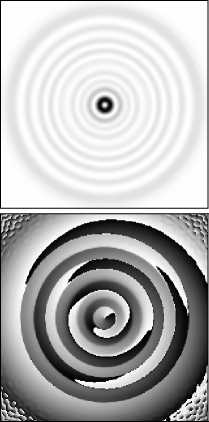
Рис. 7. Восстановление моды ГЛ (n,m)=(8,–1) после прохождения непрозрачного препятствия размером 0,528 мм: поперечное распределение интенсивности (1, 3 строки) и фазы (2, 4 строки) на различных расстояниях

Более быстрое восстановление мод, имеющих в структуре большое количество колец, может быть связано с соотношением общей энергии пучка и той части, что закрывается препятствием. Однако даже наличие весьма крупных препятствий, которые могут закрывать целиком центральное кольцо моды, не исключает возможности их восстановления (см рис. 7). Важно, что восстанавливается полная структура пучка – не только интенсивность, но и фаза: винтовой характер фазы в центральной части наблюдается уже на расстоянии 10 мм после прохождения препятствия размером 0,528 мм. Также, на рис. 7 можно видеть (начиная с расстояния 250 мм) кольцевую расходящуюся «тень» от препятствия. Интересно отметить визуальное сходство мод Бесселя и мод Гаусса-Лагерра с высоким радиальным индексом.

Суперпозиции мод ГЛ также имеют свойство восстанавливаться после прохождения препятствий (см. рис. 8). Разумеется, для этого необходимо использовать суперпозиции специально подобранных мод ГЛ [23], сохраняющих свою конфигурацию при распространении в свободном пространстве с точностью до масштаба и поворота. На рис. 8 видно (особенно по распределению фазы), что искажение пучка после прохождения препятствия выглядит как наложение дифрагирующей на этом препятствии волны. Чем меньше размер препятствия, тем быстрее будет расходиться дифрагирующая волна и быстрее восстановится первоначальная структура пучка. При этом расходимость самого пучка должна быть как можно меньше.

z = 0 мм

z = 10 мм

z = 50 мм

z = 100 мм

z = 150 мм

z=200 мм

z=250 мм

z=500 мм

z=1000 мм

z=2000 мм

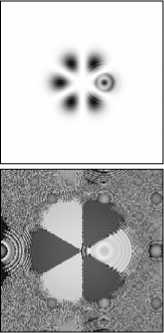
Рис. 8. Восстановление суперпозиции мод ГЛ (n,m): (0,3)+ (0,–3) после прохождения непрозрачного препятствия размером 0,195 мм: поперечное распределение интенсивности (1, 3 строки) и фазы (2, 4 строки) на различных расстояниях

Таким образом, на основе численного моделирования восстановления лазерных пучков, искаженных при прохождении препятствий, можно сделать вывод о перспективности использования пучков ГЛ для манипулирования микрочастицами в нескольких плоскостях. При этом моды ГЛ, имеющие более высокий радиальный индекс (т.е. имеющие большее количество колец), ближе по структуре к бесселевым пучкам и восстанавливаются быстрее.

Аналогичную дифракционную картину можно наблюдать и при прохождении световыми полями прозрачных препятствий. Для примера были выбраны стеклянные шарики с показателем преломления n0=1,5. Моделирование такого препятствия может осуществляться путём домножения комплексной амплитуды светового поля на фазовую функцию Ф(r,n0), соответствующую прозрачному шарику с заданными показателем преломления n0 и радиусом r0.

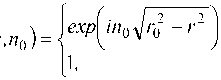
r ^ Г, ^r > ^r 0 .

z=0 мм

z=10 мм

z=50 мм

z=100 мм

z=150 мм

z=200 мм

z=250 мм

z=500 мм

z=1000 мм

z=2000 мм

Рис. 9. Восстановление моды ГЛ (n, m)=(0,1) после прохождения прозрачного препятствия в виде стеклянного (показатель преломления n0=1,5) шарика диаметром 0,195 мм

Таблица 1. Значения СКО-отклонения и интеграла перекрытия для моды ГЛ (0,1) и непрозрачного препятствия

Расстояние, мм	0	10	50	100	150	200	250	500	1000	2000	4000	Фурье
СКО	0,169	0,172	0,173	0,184	0,181	0,172	0,164	0,123	0,075	0,056	0,048	0,045
Инт. пер.	0,981	0,918	0,924	0,904	0,898	0,894	0,893	0,896	0,921	0,972	0,998	0,817

Таблица 2 Значения СКО-отклонения и интеграла перекрытия для моды ГЛ (0,1) и прозрачного препятствия

Расстояние, мм	0	10	50	100	150	200	250	500	1000	2000	4000	Фурье
СКО	0	0,724	0,238	0,281	0,272	0,256	0,242	0,177	0,107	0,075	0,067	0,063
Инт. пер.	0,950	0,439	0,851	0,841	0,843	0,841	0,843	0,867	0,911	0,967	0,997	0,810

Как видно из рис. 5 и 9, а также данных, приведенных на графиках 10, 11 и в таблицах 1,2, прозрачные препятствия вносят большие искажения в изображение, чем непрозрачные. Это объясняется тем, что в данном случае происходит не просто «вырезание» части информации (энергии) из светового поля, но её фазовое искажение. При этом прозрачный шарик работает наподобие сферической линзы, создавая в соответствующем месте резкий точечный всплеск интенсивности после его прохождения (см. рис 9).

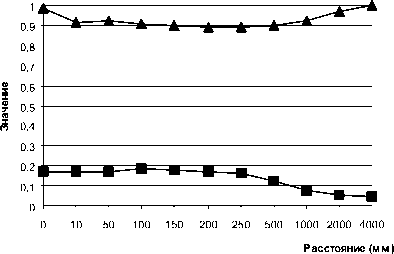
Рис. 10. Графики значений интеграла перекрытия (▲) и СКО-отклонения (■) для моды ГЛ (0,1), искажённой непрозрачным препятствием диаметром 0,195 мм

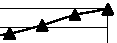
0,9

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

хх:

0   10   50  100 150 200 250 500 1000 2000 4000

Расстояние (мм)

Рис. 11. Графики значений интеграла перекрытия (▲) и СКО-отклонения (■) для моды ГЛ (0,1), искажённой прозрачным (n0=1,5) шариком диаметром 0,195 мм

Из приведенных выше результатов исследований видно, что картина и динамика искажений, вносимых прозрачными и непрозрачными препятствиями, имеет некоторые принципиальные различия. Так, для прозрачного препятствия существует отрезок протяженностью 1–4 поперечных размера изображения, на котором искажения достигают весьма значительных величин, чего не наблюдается в случае непрозрачного препятствия. Однако в дальнейшем графики ведут себя схожим образом, погреш- ности остаются примерно на одном уровне до расстояния z=250 мм (50 поперечных размеров), после чего, при дальнейшем удалении от плоскости прохождения препятствий, начинают падать. В районе z=2000 мм (400 поперечных размеров) искажения становятся практически равны исходным (при z=0), и в дальнейшем продолжают сглаживаться. Некоторый всплеск искажений в Фурье-плоскости следует отнести на счёт неточностей реализации БПФ. В целом, можно видеть схожую динамику для прозрачных и непрозрачных препятствий, отличающуюся лишь резким начальным пиком и несколько более высоким общим уровнем искажений, характерным для первых.

Восстановление после препятствий полей с угловыми гармониками

Угловые гармоники (световые воронки) имеют следующий вид

U m ( r ,ф ) = e im ^ .       (13)

Многие лазерные поля, в том числе, высшие моды Бесселя и ГЛ, удобно анализировать с точки зрения базиса УГ [24, 25]. В [20] рассмотрены различные типы лазерных пучков, содержащие УГ, в том числе амплитудная составляющая которых представляет собой плоский или гауссовый пучок. Такие поля после распространения на некоторое расстояние, приобретают довольно устойчивую конфигурацию, напоминающую моды ГЛ (с нулевым радиальным индексом (0, m ), и распространяются по похожим законам. Формирование таких полей легко реализуется с помощью фазовых ДОЭ [26].

На рис. 12 приведены результаты моделирования восстановления поля вида (13) с m =3, ограниченного круглой апертурой радиуса 1,134 мм и прошедшего через сферическую линзу. Видно, что в отличие от мод ГЛ с нулевым радиальным индексом, такие пучки имеют слабые периферийные кольца. Однако характер поведения после искажения препятствием, очень близок (сравните рис. 12 и 5).

z = 0 мм

z = 10 мм            z = 50 мм           z = 100 мм           z = 150 мм

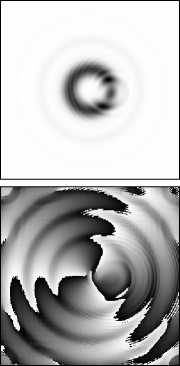
z = 200 мм

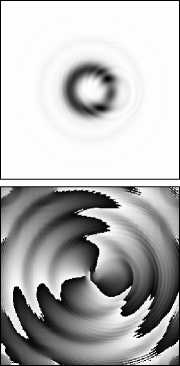
z = 250 мм

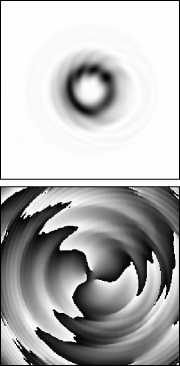
z = 500 мм

z = 1000 мм

z = 2000 мм

Рису. 12. Восстановление Фурье-образа УГ (m=3, ограничение во входной плоскости круглой апертурой радиуса 1,134 мм) после прохождения непрозрачного препятствия размером 0,195 мм:

поперечное распределение интенсивности (1, 3 строки) и фазы (2, 4 строки) на различных расстояниях

На рис. 13 можно видеть отличие УГ, «внедренных» в плоский и гауссовый пучок. В обоих случаях наблюдаются периферийные «хвосты». Однако УГ с гауссовой амплитудой восстанавливаются после препятствием быстрее, чем УГ с плоской амплитудой.

Периферийные «хвосты» в Фурье-образах полей, содержащих УГ, можно убрать, установив в спектральной плоскости ограничивающую апертуру [27]. Тогда можно получить световые пучки, визу- ально весьма схожие с соответствующими модами ГЛ вида (0, m). Моделирование восстановления таких пучков после препятствия показывает, что поведение их в этом случае практически не отличается (сравните рис. 13 и 8). Следовательно, фазовые ДОЭ, согласованные с УГ в сочетании с апертурнолинзовой оптической системой могут быть использованы для формирования лазерных пучков, очень близких по виду и свойствам к модам ГЛ с нулевым радиальным индексом.

Входная плоскость

Спектральная плоскость

∆ z=500 мм

∆ z=1000 мм

∆ z=2000 мм

Рис. 13. Восстановление суперпозиции УГ (m=3,–3), «внедренной» в плоский (две верхние строки) и в гауссовый (две нижние строки) пучок, во входной и спектральной плоскостях, а также после прохождения непрозрачного препятствия на различных расстояниях (поперечное распределение интенсивности – 1, 3 строки, фазы – 2, 4 строки)

z=0 мм

z=10 мм

z=50 мм

z=200 мм

z=250 мм

z=500 мм

z=100 мм

z=1000 мм

z=150 мм

z=2000 мм

z=0 мм

z=10 мм

z=50 мм

Рис. 14. Восстановление Фурье-образа суперпозиции УГ (m=4,–4; ограничение в спектральной плоскости круглой апертурой радиуса 1,27 мм) после прохождения непрозрачного препятствия размером 0,195 мм: поперечное распределение интенсивности (1, 3 строки) и фазы (2, 4 строки) на различных расстояниях

z=100 мм z=150 мм

z=200 мм z=250 мм z=500 мм z=1000 мм z=2000 мм

Рис. 15. Восстановление Фурье-образа суперпозиции УГ (m=4,–4; ограничение в спектральной плоскости круглой апертурой радиуса 1,27 мм) после прохождения прозрачного шарика диметром 0,195 мм: поперечное распределение интенсивности (1, 3 строки) и фазы (2, 4 строки) на различных расстояниях

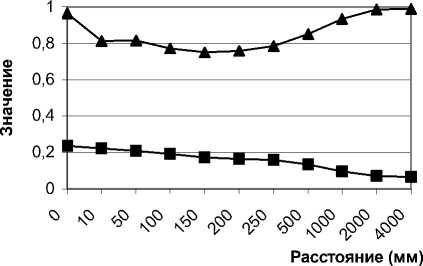
Рис. 16. Графики значений интеграла перекрытия (▲) и СКО-отклонения (■) для суперпозиции УГ (-4)+(4), искажённой непрозрачным препятствием диаметром 0,195 мм

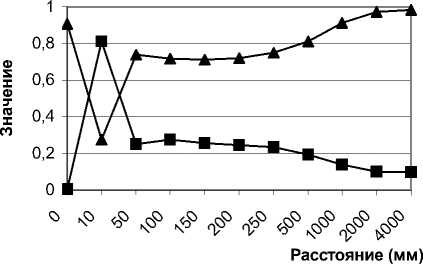
Рис. 17. Графики значений интеграла перекрытия (▲) и СКО-отклонения (■) для суперпозиции УГ (-4)+(4), искажённой прозрачным шариком диаметром 0,195 мм

Таблица 3. Значения СКО-ошибки и интеграла перекрытия для композиции УГ (-4)+(4) и непрозрачного прпятствия

Расстояние	0	10	50	100	150	200	250	500	1000	2000	4000	Фурье
СКО	0,236	0,223	0,209	0,191	0,172	0,166	0,159	0,134	0,096	0,071	0,065	0,064
Инт. пер.	0,965	0,814	0,817	0,772	0,750	0,757	0,785	0,851	0,935	0,986	0,990	0,897

Таблица 4. Значения СКО-ошибки и интеграла перекрытия для моды композиции УГ (-4)+(4) и прозрачного прпятствия

Расстояние	0	10	50	100	150	200	250	500	1000	2000	4000	Фурье
СКО	0,005	0,813	0,251	0,275	0,255	0,246	0,235	0,193	0,138	0,102	0,097	0,090
Инт. пер.	0,908	0,274	0,738	0,717	0,710	0,720	0,748	0,812	0,912	0,974	0,983	0,884

Численная оценка внесенных искажений (данные, приведенные на графиках 16, 17 и в табл. 3, 4) подтверждает выводы о схожести поведения композиций УГ и мод ГЛ соответствующих порядков, сделанные на основе визуального анализа. Мы имеем схожую динамику восстановления после прохождения как прозрачных, так и непрозрачных препятствий.

Заключение

Проведённые вычислительные и натурные эксперименты показали, что лазерные пучки, содержащие угловые гармоники, обладают различными свойствами восстановления после препятствия, которым может служить захваченная для манипулирования микрочастица. Наиболее быстро восстанавли- ваются пучки, согласованные с модами Бесселя. При этом «скорость» восстановления зависит от масштаба моды Бесселя, связанного с минимальным углом отклонения конических волн. Экспериментальные результаты показали, что бесселевы пучки различных порядков, но одинакового масштаба восстанавливаются примерно одинаково.

На основе численного моделирования восстановления лазерных пучков, искаженных при прохождении препятствий, можно сделать вывод о перспективности использования пучков Гаусса-Лагерра для манипулирования микрочастицами в нескольких плоскостях. При этом моды Гаусса-Лагерра, имеющие более высокий радиальный индекс (т.е. имеющие большее количество колец), ближе по структуре к бесселевым пучкам и восстанавливаются быстрее. Однако моды ГЛ с нулевым радиальным индексом проще реализовывать. Например, с помощью фазовых ДОЭ, согласованных с угловыми гармониками в сочетании с апертурнолинзовой оптической системой.

Работа выполнена при поддержке российско-американской программы « Фундаментальные исследования и высшее образование» (BRHE), грантов Президента Российской Федерации МД-209.2003.01 и НШ-1007.2003, а также гранта РФФИ 05-01-96505.