Восстановление связности линий на бинарных изображениях древовидных структур

Развитие вычислительной техники дало возможность автоматизировать решение ряда медицинских задач, как правило, диагностических. В частности, существует ряд практических задач анализа изображений в медицине, связанных с диагностикой состояния кровеносной системы (рис. 1). К ним относятся, например, задачи анализа сосудистой системы сердца и сосудистой системы глазного дна [1]. Существующие методы анализа таких изображений [2] позволяют выделять сосуды и оценивать их геометрические параметры, которые используются затем для диагностики заболеваний.

Рис. 1. Изображение сосудистой системы (сердца)

Однако часто для анализа доступны некачественные изображения (малоконтрастные, с малым отношением сигнал/шум), что имеет место, в частности, в случае использования рентгеновской ангиографии с низким уровнем излучения для регистрации изображений кровеносной системы сердца. В этих случаях изображение, полученное традиционными методами обработки, содержит разрывы линий. Другой причиной возникновения разрывов является утоньшение или полное исчезновение кровотока на отдельных участках сосудов. Это явление в медицинской практике называется «стенозой» [3].

Разрывы линий на изображениях препятствует решению таких задач, как поиск узлов в древовидных структурах, оценка толщины линий, получение структурной информации о сосудах и т. д. Поэтому возникает задача устранения разрывов линий на изображениях.

В данной работе для восстановления связности линий на бинарных изображениях предлагается использовать функцию специального вида, которую по аналогии с теорией классификаторов будем называть решающей. Главной целью исследования является оценка возможности получения древовидной структуры с использованием геометрических параметров разрывов.

Задача восстановления связности линий состоит из трех основных этапов:

• 1.    Поиск точек разрыва.

• 2.    Поиск оптимальных участков соединений.

• 3.    Гладкое соединение заданных концевых точек линий.

Поиск точек разрыва

Для поиска концевых точек линий на изображении реализован подход, основанный на морфологической обработке скелета исходного изображения. Подход состоит в сканировании скелетизованного изображения маской 3х3. Отсчёт изображения признаётся точкой разрыва при следующих конфигурациях масок (с точностью до поворота) (рис. 2):

Рис. 2. Конфигурации масок, соответствующие точкам разрыва линий (серый – объект, белый – фон)

Поиск оптимальных участков соединений

Поиск оптимальных участков соединений состоит в нахождении таких пар точек разрыва, которые должны быть устранены (рис. 3).

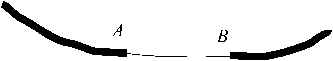
Рис. 3. Оптимальные участки соединения

На рис. 3 оптимальными участками соединения являются участки AB и CD.

Пары точек разрывов, соответствующие оптимальным участкам соединений, должны удовлетворять следующим условиям:

1) расстояние между разрывами должно быть как можно меньше;

2) направления линий должны быть согласованными, т.е. не давать изгибов линий при соединении.

Условие согласованности направлений требует оценивать направления линий в окрестностях их концевых точек. Данная задача решается путём усреднения вектора, соединяющего точку разрыва со связными с ней точками внутри окна заданных

Для устранения вышеуказанного недостатка может быть использована модификация этого метода. Чтобы наиболее удалённые точки, связанные с центром маски, оказывали меньшее влияние на оценку касательной, можно вычислять средневзвешенный вектор, соединяющий точку разрыва со связными с ней точками внутри окна заданных размеров.

В этом случае точкам линии внутри окна W приписываются веса w(m, n), убывающие с ростом удаленности от точки разрыва, а вместо формул (2) и (3) используются (4) и (5).

S mw ( m , n ) F_mn

— ( m, n ) e W m —----------------

^S Fmn

( m, n ) e W

,

S ^{nw ( m} , ⁿ) Fmn - _ ( m,n )e W

^S Fmn

( m, n ) g W

,

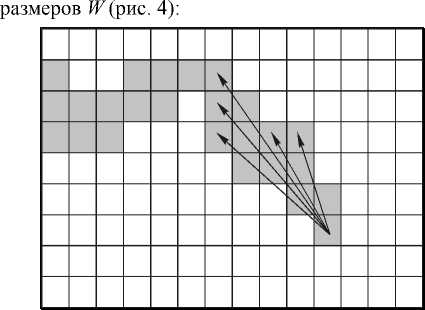
Рис. 4. Оценка направления линий

Т.е. вектор, задающий направление линии в окрестности точки разрыва, находится так:

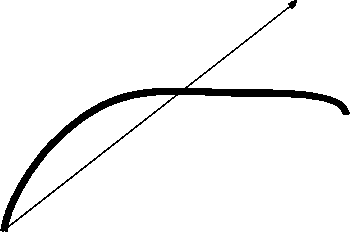
Рис. 5. Оценка направления линии в случае большой кривизны

Если же изображение содержит сильно изогнутые линии, то и такой подход может не дать результатов. Направления линий в окрестностях точек разрыва окажутся несогласованными, и разрыв не будет устранён. В этом случае можно применить ещё более точное оценивание направлений линий: путём аппроксимации их (линий) участков в окрестностях точек разрыва кривыми второго порядка:

t — { m , n } ,

, ^{S m}F^mn — (m , n )eW m —--------------- ,

^S Fmn

( m , n ) e W

^{S   nF}mn

- ( m, n ) e W n —                    ,

^S Fmn

( m, n ) e W

где t - вектор, задающий направление линии в окрестности точки разрыва; F_mn =1, если ( m, n )-й отсчёт связан с центральным отсчётом маски и 0 – в противном случае.

Следует отметить, что данный подход к оценке направлений линий является достаточно грубым и, следовательно, плохо работает в случае большой кривизны линий в окрестностях точек разрыва (рис. 5).

A 20 x 2 ⁺ A 02 У 2 ⁺ A 11 ^ХУ ⁺

⁺ A 10 x ⁺ A 01 ^{y +} A 00 = ⁰

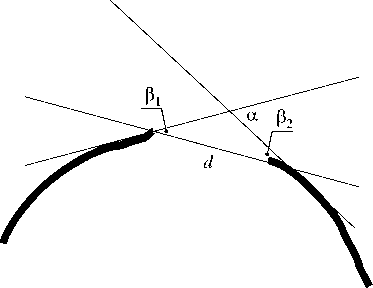
Рис. 6 – Параметры, используемые при поиске оптимальных пар соединений

После того, как найдены все концевые точки линий и оценены направления касательных к ним, можно находить оптимальные участки соединений.

Для установления соответствия между соединяемыми концевыми точками линий, предлагается учитывать следующие параметры (рис. 6):

• •    расстояние между точками разрыва;

• •    угол между касательными к линиям в окрестностях концевых точек;

• •    угол между касательной к линии в окрестности рассматриваемой точки разрыва и прямой соединяющей две точки разрыва.

Эти параметры учитывались решающей функцией. Каждая точка разрыва соединялась с той точкой разрыва, для которой решающая функция была минимальной.

Пусть N – количество точек разрыва на изображении;

B = { bi } i = i — множество точек разрыва;

Для всех i = 1,...,N решается задача:

f ( bi,bj ) ^

min , j = 1,..., N

j * i где f(bi,bj) - решающая функция.

Экспериментально было установлено, что наиболее подходящей платёжной функцией является функция вида:

+ m-

d-c^osaij >  ^amin, + 0, иначе;

^{+ n}1 1

d,c^os^e_u > ^emin,

+

^{+ n}2 "

0, иначе;

dc'⁴'2ij > ^вmin, 0, иначе;

где p,q,r1,t2,m,n1,n2, a min, ^min - экспериментально подбираемые параметры; dij - расстояние между i-м и j-м разрывами; αij - угол между каса- тельными к линиям в окрестностях точек разрыва;

β1ij, β2ij - углы между касательными к линии в ок- рестностях рассматриваемых точек разрыва и прямой, соединяющей эти точки.

Первые четыре слагаемых означают, что чем меньше расстояние между точками разрыва. и чем более согласованы направления линий в них, тем больше вероятность, что данные точки принадлежат одной линии.

Последние три слагаемых являются штрафами. Они не позволяют соединять точки разрыва, распо- ложенные слишком близко друг к другу, но направления линий, в которых существенно различаются.

Гладкое соединение заданных концевых точек линий

Для некоторых задач недостаточно знать только то, какие точки разрыва должны быть соединены. Необходимо также знать, как они будут соединены. Используя информацию о направлениях касательных к линиям в точках разрыва необходимо произвести гладкое соединение. В найденных аналогах для этого используется поле направлений [1]. Однако оно применяется к изображениям квазипериоди-ческих структур. Изображения сосудистых систем к этому классу не относятся. Поэтому в данной работе использовались эрмитовы сплайны, так как они просты при построении и позволяют сохранить гладкость линий при соединении точек разрыва.

Восстановление древовидной структуры

При решении задачи восстановления связности может быть априорно известно, что линии на получаемом изображении должны составлять древовидную структуру. Например, такое условие может присутствовать при восстановлении связности линий на изображениях сосудистой системы сердца.

В этом случае необходима сегментация (выделение объектов) на разрывном бинарном препарате. Сегментация позволит проконтролировать, чтобы любые два сегмента были соединены не более, чем один раз, что необходимо для получения древовидной структуры.

Для того чтобы гарантировать получение дерева, необходимо найти образуемые найденными соединениями циклы. Поиск циклов может быть осуществлён любым алгоритмом поиска циклов в графе [4]. В данном случае вершинами графа являются сегменты изображения, а рёбрами – соединения между сегментами.

После обнаружения цикла одно из соединений, входящих в него (цикл), должно быть разорвано. Как правило, выбирается соединение, расположенное дальше всех от корня дерева. Вопросы, связанные с поиском корня дерева в данной работе не рассматриваются.

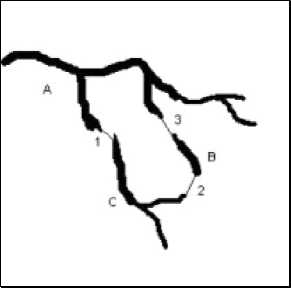
Рис. 7. Нарушение древовидной структуры. Буквы - найденные сегменты изображения, цифры - соединения

Поиск циклов и устранение одного из соединений, входящих в цикл повторяется до тех пор, пока все циклы не будут устранены.

Так, на рис. 7 должно быть устранено соединение 2 (Корень дерева располагается слева).

Исследования

Было проведено исследование зависимости качества восстановления связности от кривизны линий. Результаты приведены в таблице 1 и на рис. 8.

Было также проведено исследование устранения циклических соединений сосудов для получения древовидной структуры. На рис. 9 из двух соединений, образующих циклы, одно было разорвано.

Проведенные исследования показали, что разработанные для бинарных изображений алгоритмы позволяют получить древовидную структуру. Настройка коэффициентов решающей функции позволяет устранять большинство разрывов линий.

Таблица 1

Зависимость качества восстановления связности от кривизны линий

Радиус кривизны	Разрыв устранен
∞	Да
20	Да
15	Да
5	Да
2	Нет

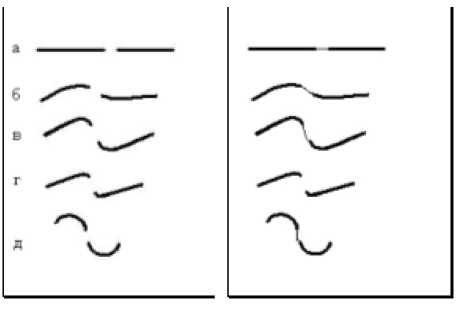
Рис. 8. Зависимость качества восстановления связности от кривизны линий: а) радиус кривизны бесконечен; б) радиус кривизны равен 20; в) радиус кривизны равен 5; г) радиус кривизны равен 2; д) радиус кривизны равен 15.

Рис. 9. Устраненное циклическое соединение

Заключение

На основе анализа геометрических характеристик разрывов разработан алгоритм, который позволяет восстанавливать связность линий на бинарных изображениях, получать древовидную структуру, описывающую сосудистую систему. Экспериментально подтверждена возможность использования метода для диагностики заболеваний, а также для задач обработки немедицинских изображений, в том числе интерферограмм [5].

Возможно повышение качества работы алгоритма путем расширения множества рассматриваемых признаков, характеризующих разрывы на изображении. Например, в данной работе не учтена толщина линий в окрестностях точек разрыва. Дальнейшие исследования будут посвящены проверке применимости алгоритма к обработке интерферограмм, а также для получения связных контуров, используемых для решения многих прикладных задач обработки изображений.