Возбуждение квантового осциллятора в тепловом равновесии: описание с помощью спектральной функции

Интенсивное развитие технологий генерации лазерных импульсов с заданными параметрами, в том числе ультракоротких импульсов (УКИ) [1, 2], обуславливает необходимость разработки аналитических методов описания взаимодействия таких импульсов с веществом, сочетающих в себе эффективность, простоту и физическую ясность процесса.

Передача энергии от УКИ к веществу теоретически исследовалась в ряде недавних работ [3-6]. Статья [3] посвящена расчету передачи энергии от интенсивного фемтосекундного лазерного импульса к электрону в простых диэлектриках в рамках теории функционала плотности, зависящего от времени. В работе [4] исследовалось взаимодействие одноцикловых импульсов атто- и фемтосекундной длительности с алмазом с использованием уравнений Кона - Шэма и Максвелла.

• В работе [5] была точно измерена когерентная передача энергии между инфракрасными импульсами суб цикловой длительности и осциллирующими молекулами в водном растворе.

Процесс был описан с помощью теории функционала плотности, что позволило определить динамические характеристики среды, такие как собственные частоты колебаний молекул и дипольные моменты переходов.

В работе [6] мы проанализировали поглощение ультракоротких импульсов в среде с учётом эффектов распространения с использованием полного коэффициента поглощения, который описывает специфику сверхбыстрого электромагнитного взаимодействия в объеме вещества.

Квантовый осциллятор - уникальная квантово-механическая модель, допускающая точное решение для любой интенсивности внешнего возмущения [7,8]. Эта модель имеет широкое применение, поскольку описывает как ряд реальных физических объектов, так и состояние вещества вблизи положения равновесия. Поэтому детальное исследование особенностей возбуждения квантового осциллятора имеет как фундаментальное, так и прикладное значение.

Модель квантового осциллятора была использована для описания возбуждения квантовых систем униполярными субцикловыми импульсами в приближении внезапных возмущений, когда вероятность процесса выражается через электрическую площадь импульса [9]. В работе [10] исследовалось сверхбыстрое управление колебательными состояниями полярных молекул, возбуждаемых субцикловыми униполярными импульсами. В рамках приближения электрической площади импульса это описание было распространено на ангармонические квантовые осцилляторы.

Возбуждение квантового осциллятора многоцикловыми импульсами произвольной амплитуды было подробно исследовано в работе [11]. В частности, для гауссовой и огибающей импульса в форме гиперболического секанса были определены особенности вероятности возбуждения в зависимости от длительности импульса и его несущей частоты. В [12] рассмотрение было распространено на вейвлеты и униполярные импульсы вне приближения внезапных возмущений.

В указанных работах предполагалось, что квантовый осциллятор находится в одном из стационарных состояний до воздействия импульса.

Цель данной работы — получить аналитическое описание процесса передачи энергии от лазерного импульса к квантовому осциллятору, находящемуся в тепловом равновесии, и выявить особенности этого процесса с использованием формализма спектральной функции.

2.    Общие формулы

Начнём с формулы Швингера для вероятности возбуждения квантового гармонического осциллятора между стационарными состояниями [7]:

Wn^f =   ',v^nf -ⁿL2 ^Пг (v)Ре^-^ ,n_f >  п_г,                     (1)

П { !

где L^ — полином Лагерра, v — безразмерный ключевой параметр, который можно выразить в виде [11]:

_ Aclass

v    hw0 , wo — собственная частота осциллятора, Aciass — работа внешней силы, совершаемая над классическим осциллятором, связанным с квантовым, т.е. имеющим те же характеристики, что и квантовый осциллятор.

Определим распределение вероятности передачи энергии квантовому осциллятору в состоянии теплового равновесия (спектральную функцию) согласно следующему выражению [13, 14]:

dWt (Е) dE

^  (Wk)тS(E - khw), k=nf—П{

здесь угловые скобки обозначают усреднение по тепловому равновесию при температуре Т,

^Wk-n _f-n=T = expl —и coth( —⁰ ^ +k —⁰ }lk { —-—- —- ^ ,         (4)

\ k-nf Пг/1                \2T ) 2Т J k\sinh(E//2Т )),           u где Ik(z) - модифицированная функция Бесселя, температура измеряется в энергетических единицах.

Интересно отметить, что выражение (4) совпадает с формулой для спектральной функции, описывающей фотопоглощение электронными центрами в твердых телах при наличии сильной электрон-фононной связи [15]. В последнем случае безразмерный параметр и равен половине тепловыделения при электронном переходе, к — число испущенных/поглощенных фононов.

Определим безразмерную вероятность передачи энергии по формуле

W_T (Е ) = h^o ^CW(E).

СЕ

Для получения замкнутого аналитического выражения заменим суммирование в формуле (3) интегрированием по к, в результате получим

^{W t} (Е,. )« ^Wk . . ^(и» = ^exp{^-v^coth[^ ₊ ^Е}i_E/^( —h(^T ))• ⁽⁶⁾

Сравнение приближенной формулы (6) и (3), умноженной на Ншо, показано на рис. 1. Расчет по (3) проводился с заменой дельта-функции на лоренцеву функцию со спектральной шириной у = 0.01 отн. ед.

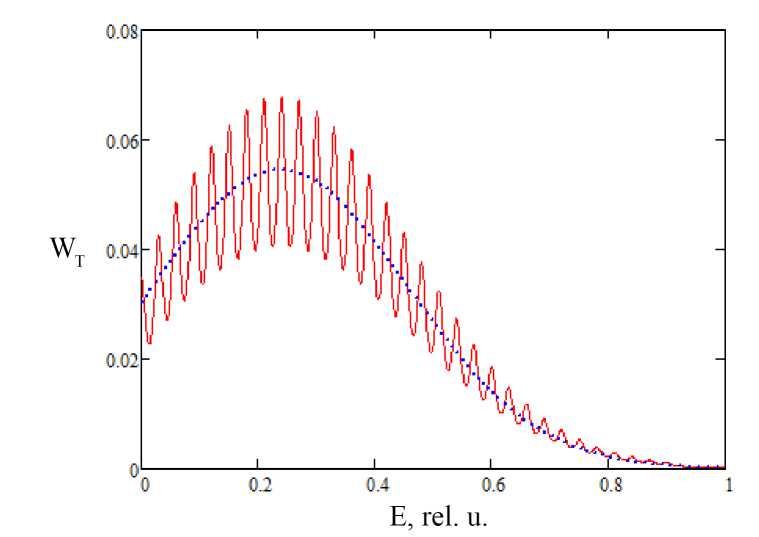
Рис. 1. Вероятность передачи энергии от внешней силы квантовому осциллятору, рассчитанная по выражению (3), умноженному на энергию кванта (сплошная линия) и по приближенному выражению (6) (пунктирная линия) при и = 8, Т = 0.1 отн. ед., ^о = 0.03 отн. ед.

Из рис. 1 видно, что приближенное выражение (6) представляет собой среднюю линию по осциллирующей функции, определенной формулой (3).

Рассмотрим два предельных случая формулы (6), а именно, предельные значения высокой и низкой температуры, для которых можно получить простые выражения.

Высокая температура

Этот случай соответствует неравенству: Т >  Ншо- Тогда мы можем использовать следующее представление модифицированной функции Бесселя:

I k (z)

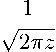
exp{z - i}.

Используя это представление, вместо (6) получаем следующее выражение:

и,у (Е) ^ -Д^= exp{- (- I - A aA }. Д 4тг1¹А_С 1 _ав          4TA ci _as

Из этого равенства следует, что вероятность передачи энергии достигает максимума при переданной энергии, равной работе, совершаемой над ассоциированным классическим осциллятором внешней силой:

^Emax — ^Aclas

и соответствующая вероятность равна: Wt (Emax) ~ 1шд/ Д 4^TA_c i _as.

Отметим, что наиболее вероятная передача энергии (9) совпадает со средней переданной энергией квантовому осциллятору [13, 14].

Дисперсия распределения передачи энергии (8) в случае высоких температур равна

ОЕ — vTA cia^.                             (10)

Таким образом, дисперсия в этом случае увеличивается с увеличением работы, совершаемой соответствующим классическим осциллятором.

Низкая температура

Когда T < Кшд из общей формулы (6) после некоторых алгебраических вычислений можно найти, что вероятность переданной энергии определяется выражением

^W T ^(Е ) ~ ^Ee ^eXP{- р Щ~ ^[Е — ^A clas + ^Е ^ⁿ(^Aclas/^E)]}'

(И)

Видно, что зависимость вероятности от температуры в этом пределе исчезает.

Простой анализ показывает, что функция (11) имеет максимум при той же переданной энергии (9), что и при высоких температурах, при этом W_T(Emax ) ^ ^Йшд / 2^A_ci_as, а дисперсия спектральной функции равна

; ш 2

ОЕ — —^^^^^.

V 2^A clas

Таким образом, дисперсия энергии уменьшается с увеличением работы A_c i _as по сравнению с пределом высокой температуры (10).

Вероятность передачи энергии, рассчитанная по формуле (6), представлена на рис. 2 для промежуточного случая: Ъшд — T. Видно, что равенство (9) приближенно справедливо и в этом случае. Незначительное отклонение от (9) наблюдается при малых по сравнению с энергией кванта осциллятора значениях передаваемой энергии Е.

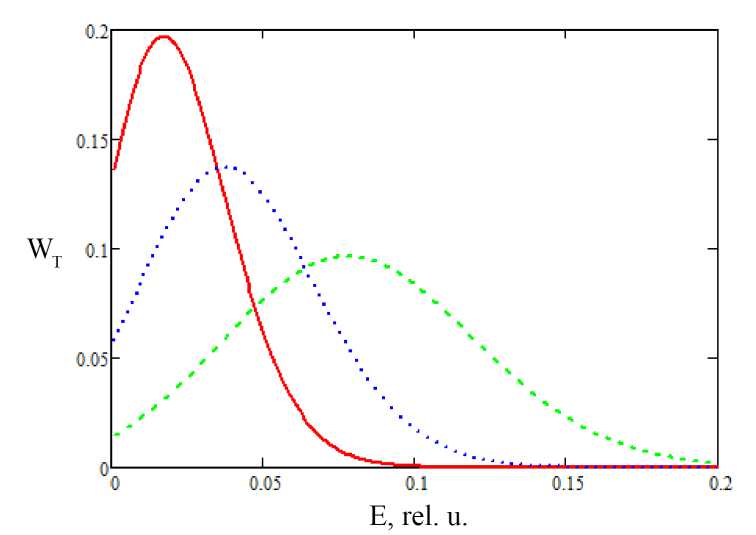
Рис. 2. Вероятность передачи энергии квантовому осциллятору при различных значениях параметра и: сплошная линия ~ = = 2. пунктирная линия - = = 4. штриховая линия - = = 8. Т = ш₀ = 0.01 отн. ед.

Вероятность передачи энергии в максимуме Из вышеизложенного вытекают следующие формулы в терминах безразмерного параметра и (2):

Emax — Ьшо П,

Wt (Emax , Т> Нш_о ) « ^ЕА 1                     (14)

Wt (Emax,Т< hwo )

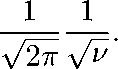
Таким образом, в случае высоких температур максимальная вероятность передачи энер гии меньше, чем в случае низких температур при том же значении ключевого параметра и.

Зависимость вероятности передачи энергии в максимуме от параметра и для различных температур, рассчитанная по формуле (6), представлена на рис. 3. На этом рисунке введен безразмерный параметр г — Ьшо/2Т.

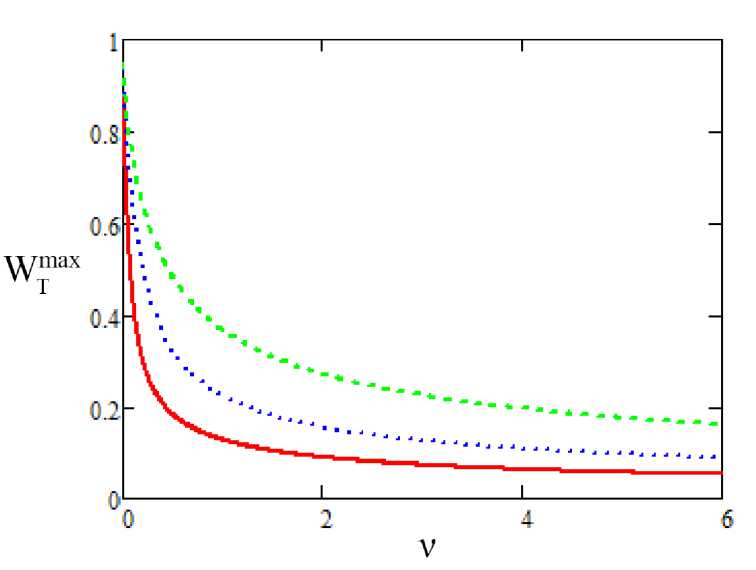
Рис. 3. Зависимость вероятности передачи энергии в максимуме от ключевого параметра и для различных температур: сплошная линия - г=0.1 (высокая температура), пунктирная линия - г=0.3 (промежуточная температура), штриховая линия - г=10 (низкая температура)

3.    Выводы