Возбуждение магнитосферного МГД-резонатора нестационарными гидромагнитными волнами внемагнитосферного происхождения

Настоящая статья публикуется за статьей автора [Мазур, 2009] и является ее продолжением. В рамках той же модели среды мы теперь исследуем то же явление, но не предполагаем колебания монохроматическими. Изучение нестационарных, широкополосных колебаний будем осуществлять с помощью разложения их в интеграл Фурье:

C( x , t ) = j %( x , _Ю ) e ^— i ^{to t} d to.                               (1)

—TO

Для упрощения записи формул здесь опущена зависимость от координат y и z , имеющая стандартный вид exp( ik y y + ik z z ). Функция c, ( x , to) при заданном значении частоты описывает пространственную структуру монохроматической волны. Она подробно изучена в [Мазур, 2009], и мы широко будем использовать результаты этой работы, а также введенные там обозначения, не повторяя их описание в настоящей статье.

Фурье-гармонику ς%( x , ω) можно представить в виде

%( x , to) = C w (to) c( x , to).                              (2)

Здесь ςˆ( x , ω) – некоторое стандартное решение для данной частоты, которое можно считать определенным образом нормированным, а C _W (ω) – комплексный множитель, играющий роль амплитуды волны. Он снабжен индексом W, поскольку в задаче о падении волны из солнечного ветра следует считать заданной амплитуду падающей волны (Wind – ветер). Впрочем, совершенно ясно, что величина

C _W (ω) определяет амплитуду фурье-гармоники во всем пространстве. Согласно принципу суперпозиции, функция ς( x , t ), задаваемая соотношениями (1) и (2), будет описывать возможное колебание среды при произвольной функции C _W (ω).

Все нестационарные колебания можно условно разделить на два, в определенном смысле противоположных, класса. К одному относятся колебания с регулярной, вполне определенной зависимостью от времени, а к другому – стохастические колебания, для которых зависимость от времени носит случайный, непредсказуемый характер. Для первого класса функция C _W (ω) является регулярной функцией частоты, а для второго ее следует рассматривать как случайную функцию, принадлежащую некоторому статистическому ансамблю. Как регулярные колебания можно рассматривать сравнительно ограниченный круг явлений, таких как крупномасштабные нестационарные колебания, вызываемые разного рода переходными процессами – SC или суббуревым взрывом. Но большая часть колебаний магнитосферы носит скорее стохастический характер. Настоящая статья посвящена регулярным колебаниям, стохастические колебания рассмотрены в третьей статье цикла, публикуемой за настоящей.

Падающая и отраженная волны

Решение для монохроматической волны в солнечном ветре представим в виде суммы падающей и отраженной волн:

%( x , to) = c in ( x , to) + c out ( x , to). (3)

Согласно формуле (65) статьи [Мазур, 2009]

S in ( x , to) = C w (to) [ P o ( x ) c S ( x ) ] ^1/2 exp [ - i toT_s ( x ) ] , (4)

S out ( x , to) = C w (to) R (to) [ P o ( x ) c s ( x ) ] ^1/2 X

X exp [ i toT_S( x ) ] .

Напомним, что x

Ts( x) = J xM dx cs( x')

есть время пробега с локальной скоростью звука от магнитопаузы до точки x в солнечном ветре, R (to) -комплексный коэффициент отражения. Отметим, что стандартная функция S( x , to), фигурирующая в соотношении (2), в солнечном ветре, согласно (3)(5), имеет вид

S(x, to) = [po(x)cs(x)]1/2 X x{exp [-i toTs (x)] + R (to) exp [ i toTs (x)]}.

Функция g( x , t ) точно так же разбивается на сумму падающей и отраженной волн:

S( x , t ) = S in ( x , t ) + S out ( x , t ).

Выражения для них очевидным образом следуют из соотношений (1) и (3)-(5).

На магнитопаузе, при x = x _M, имеем

S in ^{( x} M , ^{to )} = ⁽ P w ^c sw ^{) 1/2 C} w^{( to )} .

Отсюда

Sin(xM, t) = (Pwcsw)1/2 Cw(t), где обозначено то

C w ( t ) = J C w (to) e ^— i ^to t d to.

—то

Падающую волну в равной степени можно задавать как функцией C _w(to), так и функцией C _w( t ). Последняя обладает большей наглядностью - она непосредственно описывает временную зависимость падающей волны на магнитопаузе. Но в ряде случаев результат проще выражается через функцию C _w (to). Поэтому мы будем использовать обе функции.

В качестве примера будем рассматривать падающую волну, представляющую собой волновой импульс, который представим в виде

C w ( t ) = C ф ^ T j .                               (6)

Здесь C - амплитуда, а ф(6) - функция порядка единицы в области |9| < 1, быстро стремящаяся к нулю при 6^+да. Такие свойства функции ф(9) означают, что T - характерная длительность волнового импульса, а характерный масштаб изменения фурье-образа C _w(to) по переменной to есть 1/ T .

В произвольной точке солнечного ветра при x > x _M имеем

S in ( x , t ) = [ P o ( x ) c s ( x ) ] ^1/2 C w [ t + T s ( x ) ] .            (7)

Временная эволюция падающего возмущения в точке x имеет тот же вид, что и в точке xM, но происходит на время ts(x) раньше. Это означает, что каждый малый участок волнового поля движется к магнитопаузе с локальной скоростью cs(x).

Рассмотрим, как меняется пространственная форма возмущения для функции вида (6). Пусть x = x _s( t ) - функция, обратная к t _s( x ). Чтобы продолжить ее в область t <0, положим x _s( t )= x _s(- 1 ). Эта функция дает координату точки, бегущей из x =<» к магнитопаузе и, после отражения от нее в момент времени t =o, убегающей назад. В каждой данной точке она движется с локальной скоростью +c_s( x ). Предполагая значение t фиксированным, разложим функцию T_s( x ) вблизи точки x = x _s( t ) до линейного члена:

T s ( x ) = | t | +

x — x _s ( t ) ^c s [ ^x s⁽ t ) ]

Подставляя это разложение в (7), для функции вида (6) имеем при t

Sin (x, t) = C {Po [xs (t)] cs [xs (t)]}1/2 Ф x — xs( t) cs( xs( t)) T

Это выражение описывает волновой пакет, центр которого перемещается по закону x = x _s( t ), т. е. движется со скоростью — c _s( x _s( t )). Ширина пакета A x ~ c _s ( x _s ( t )) T . Легко увидеть, что линейное разложение применимо, если ширина пакета A x много меньше характерного масштаба неоднородности солнечного ветра l _w, т. е. при T <<  l _w/ c _s. Кроме того, выражение (8) неприменимо при 1 1 1 <  T , когда волновой пакет достигает магнитопаузы и происходит процесс его отражения.

Пространственно-временная эволюция отраженной волны дается функцией

Sout(x, t) = [Po(x)cs(x)]1/2 X то

X J C _w(to) R _w(to)exp [ — i toT_s( x ) ] d to.               (9)

—то

В статье [Мазур, 2oo9] показано, что для всех значений to, кроме узких окрестностей собственных частот магнитосферного резонатора | to — to _n | <  v n , можно считать R (to)=-1. Будем предполагать, что характерный масштаб изменения Ato функции C _w (to) много больше v n . Тогда при вычислении интеграла (9) в главном порядке по малому параметру v n /Ato наличием указанных окрестностей можно пренебречь. В результате получим

S out ^{( x} , t ) = ^— [ P o ^{( x} ) ^c s ^{( x} ) ] ^{1/2 C} w [ t ^{— T} s ^{( x} ) ] .

Волновое возмущение полностью отражается. При отражении оно меняет знак и после этого движется с локальной скоростью c _s( x ).

Полное возмущение есть суперпозиция падающей и отраженной волн. Для функции C _w( t ) вида (6) при (- 1 )>> T в сумме (3) имеется только падающее возмущение S in ( x , t ), а при t >> T - только отраженное S o _ut( x , t ). При 1 1 1 <  T падающее и отраженное возмущения интерферируют. Отметим, что на магнитопаузе в результате интерференции s ( x _М , t )=o при любом t и для любой падающей волны C _w( t ).

Описанная картина отражения справедлива в нулевом порядке по малому параметру vn/Δω. В следующем порядке отражение уже не является полным. Малая часть энергии падающей волны проникает в магнитосферу, возбуждая собственные моды магнитосферного резонатора и создавая резкое усиление возмущения в окрестности альфвеновского резонанса, где происходит диссипация его энергии. Кроме того, имеются любопытные изменения в картине отраженного возмущения. В этом порядке выявляется наличие ма- лых по амплитуде квазимонохроматических волн на собственных частотах магнитосферного резонатора. Эти волны представляют собой медленно затухающее излучение собственных мод резонатора, которое является еще одним каналом потерь его энергии. Все эти вопросы рассмотрены в следующих разделах статьи.

В заключение этого раздела вычислим полную энергию падающего возмущения, предполагая его ограниченным по времени. Общее выражение для плотности энергии МГД-волн имеет вид [Ландау, Лифшиц, 1982]

W

B 2 + P o v² + P P 8π    2    2ρ₀ ^.

Поскольку в солнечном ветре c A << c S , то МГД-волну можно считать просто звуком. Тогда первым членом в (10) можно пренебречь, а второй и третий члены при усреднении по времени равны между собой. Эти выводы нетрудно получить из соотношений (7), (9), (10) и (63) статьи [Мазур, 2009]. В этих соотношениях фигурируют фурье-гармоники, но если эти выводы справедливы для каждой из фурье-гармоник, то они справедливы и для возмущения в целом. Таким образом,

W = P_ov² = P_o0| / d t )². (11)

Из тех же соотношений следует,  что

14 , 1 • |4j << |4 . 1 и

" ,:     =1., t)■ dt         Po( .) cs( .)

Тогда из (11) для плотности энергии, усредненной по z и y (что дает множитель 1/4), имеем w = 1'2 %2

4 ρ₀ c _S

1 1

--C ²( t + t_s ( . )).

4 c ( x )         ^S

Здесь предполагается, что время t таково, что возмущение еще не достигло магнитопаузы x = x M , так что ς( x , t ) сводится к падающей волне (7). Полная энергия падающего возмущения E _in получается отсюда интегрированием по области солнечного ветра (фактически – по области локализации падающего возмущения):

1 r                     d. 1 r

Е = 7 f C W⁽ t ^{+ T} S⁽ . ^))— = 7J C W⁽ t ^{+ T} S ) d ^T S -

4                  c ( x ) 4

xM                     S0

Учитывая условие, наложенное на величину t, интегрирование по τS можно формально распространить до τS=–∞. Тогда получаем rr

Ein = J CW(t)dt = f J |C«(») dи ■(12)

—r—r

Возбуждение магнитосферного резонатора

Выражение для монохроматической фурье-гармоники в магнитосфере, т. е. при x < x M , имеет вид

%(., и) = CM(to)i;m(., и), где

1/2

B

Cм(и) = iCw(и)l —°- I l 4пи I

1/2 δ_W

tg Ф м (и) + i ( 5 a + 5_W )

есть амплитуда возмущения в магнитосфере, q _M ( . , и) - функция, описывающая пространственную структуру монохроматической волны, выражения для нее в различных частях магнитосферы даются формулами (32)–(45) статьи [Мазур, 2009]. Эта функция и функция ςˆ( x , ω) , фигурирующая в соотношении (2), пропорциональны друг другу как функции x , но различаются множителем, зависящим от ω. В выражении (13) подразумевается, что частота положительна. Для отрицательных значений ω выражение для функции <;( . , и) следует из условия вещественности функции ς( x , t ):

%( . , и) = % * ( . , — и).

При вычислении функции ς( x , t ) с помощью преобразования Фурье (1) важную роль играют аналитические свойства %( . , и) как функции комплексного ω. Проанализируем их в той степени, которая необходима для дальнейших вычислений.

Функция % M ( . , и) при частотах, равных собственным частотам магнитосферного резонатора ω=ω n , представляет собой собственные моды резонатора %_м( . , и _n ) = % _n ( . ). Собственные моды с разными значениями n существенно отличаются друг от друга. Поэтому можно считать, что характерный масштаб изменения функции %_м ( . , и) по переменной и есть расстояние между собственными частотами Д и _n ~ т ^— П . Это означает, что ближайшие к вещественной оси особенности функции %_м ( . , и) находятся на расстоянии по порядку величины не меньшем, чем Δω n . Действительно, особенности существенно более близкие привели бы к существенно более быстрому изменению этой функции на вещественной оси.

Нули знаменателя в выражении (13), являющиеся полюсами функции %( . , и), расположены в точках ω=±ω n – iv n , т.е. на собственных частотах магнитосферного резонатора (с учетом декремента затухания). Расстояние между полюсами также равно Δω _n , но их расстояние от вещественной оси гораздо меньше: v_n <<Δω _n .

Обозначим через Δω характерный масштаб изменения спектральной функции С _W (ω) при вещественных значениях ω. Тогда, при продолжении в комплексную плоскость, расстояние от ее особенностей до вещественной оси не может быть меньше Δω. Если падающее возмущение имеет вид волнового импульса (6), то Δω~1/ T .

Из приведенного анализа видно, что если спектральная функция СW (ω) сосредоточена вблизи некоторой частоты ω0, так что ширина спектра Δω<<Δωn, то возмущение ς(x, t) в магнитосферной области мало отличается от монохроматической волны с частотой ω0. Поэтому мы сосредоточимся на противоположном случае Δω≥Δωn и ограничимся определением временной асимптотики возмущения в резонаторе.

Для определения асимптотики сместим контур интегрирования в (1) с вещественной оси в комплексную плоскость так, как это изображено на рисунке. Значение σ выберем так, чтобы прямая Imω=–σ лежала много ниже полюсов ω=±ω n – iv n , но выше всех остальных особенностей функции ς%( x , ω), т. е. v n <<σ<<Δω, Δω n . Интеграл по смещенному контуру сводится к сумме вычетов в полюсах и интегралу по прямой Imω=–σ. Последний мажорируется функцией exp(–σ t ) и асимптотически пренебрежимо мал по сравнению с вкладом полюсов. Таким образом, асимптотически

5( x , t ) = £ C n 5 n ( x ) exp( - i to n t ) + кс.

n

Из (14) следует, что

(      Y/2

C n = ПВB о   ^V '

to T

V n gn 7

C w (to n )exp( -V n t ).

Отсюда

W R = 2n V W n | C _w(to n )|² exp( - 2 V n t).              (15)

С учетом соотношения (12), имеем

W         ^V W n I C W^{( to} n )

R n = 4n----¹-------!- exp( - 2 v t ).

Е        “        2            n in         J |(Cw(to)| dto

По порядку величины при t <<1/ v n

^W R n

^Е in

~

^V W n

A ^to ,

^( x , t ) = JBB 0 £

n

1/2

ωτ

V n gn 7

C W^{( to} n X n ⁽ x ) ^X

X exp( - i to n t -V _nt ) + к.с. (14)

Это выражение представляет собой суперпозицию собственных мод магнитосферного резонатора.

Более сложное рассмотрение, которого мы приводить не будем, показывает, что характерное время переходного процесса, в течение которого в резонаторе устанавливается собственная мода, есть характерное время пробега возмущения через резонатор, т. е. величина порядка τ gn ~ l M / c AM . Подчеркнем, что это время порядка периода колебаний собственной моды 2n/to n и много меньше времени ее затухания V ^- .

Полная энергия собственной моды резонатора согласно формуле (52) статьи [Мазур, 2009] равна где C_n = C _M(to _n ) - амплитуда собственной моды, т. е. коэффициент в разложении

Полученные соотношения можно трактовать следующим образом. Магнитопауза играет роль своего рода фильтра, который пропускает гидромаг-нитные волны в узких полосах на дискретных частотах, равных собственным частотам магнитосферного резонатора. Ширины этих полос по порядку величины равны декрементам радиационного затухания собственных мод. Проникшая в магнитосферу энергия падающей волны превращается в энергию собственных мод. Эти моды затухают с полным декрементом затухания.

Особенности этого затухания рассмотрены в следующих разделах.

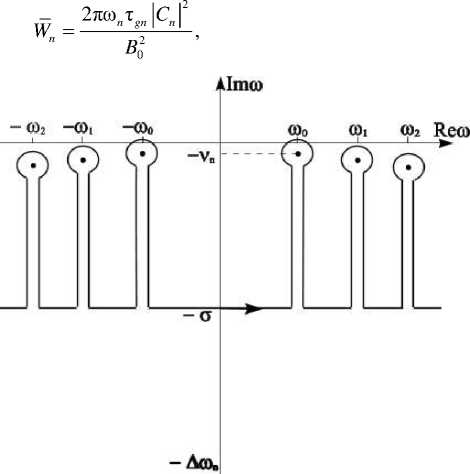
Смещенный в комплексную плоскость контур интег рирования по частоте ω .

Возбуждение альфвеновских резонансов

Для описания возмущения в окрестности альф-веновского резонанса будем использовать не функцию ς( x , t ), фурье-образ которой ς%( x , ω) имеет в точке альфвеновского резонанса конечное значение, а компоненту возмущенного магнитного поля B y ( x , t ), фурье-образ которой (см. формулы (9), (7), (25) и (П13) статьи [Мазур, 2009]) сингулярен в этой точке:

%

B y

( x , to) = i

4π k_yk_z B 0

X C M (to)^ M ( x , to).

c _A² ( x )

(to + i Y a )² - to A ( x )

X

В соотношении (16) ω A ( x )= k z c A ( x ) – альфвеновская частота, γ A =γ A ( x ) – декремент затухания альфвенов-ской волны.

Временная асимптотика интеграла

M

B y ( x , t ) = J B y ( x , to)exp( - i to t ) d to                (17)

-M

определяется полюсами фурье-образа B_y ( x , ω). Учитывая наличие в (16) полюса в точке альфвенов-ского резонанса, для множителя ς%_M ( x , ω) возьмем его значение в этой точке (формулы (44) и (61) статьи [Мазур, 2009]):

5 m ( x A (to), to) =

2 i k_z π k y

f ^ A V l A

1/2

В выражении для C _M (ω) также ограничимся полюсными членами в (13):

С „,( _Ш ) = i-B- 2

4π n

^V W n C W ⁽ ® n ) t> ^- ® n ⁺ V ).

В результате выражение для By (x, ω) можно привести к виду

1/2

В ( x , _ю ) = - 2 iY ^v A n ^{v W n} ®   x

y n V l An J

% x Cw (®n )x

® A⁽ x ) ^- ® n ⁺ i ^{( V} n ^- Y A n )

x Ij .                 (18)

V ® ^- ® A^{( x} ) + iY An ® ^- ® n ^{+ i V} n J

Здесь обозначено γ A n = γ A ( x A n ), x A n = x A (ω n ), l A n = l A ( x A n ). Выражение (18) применимо при ω>0. Для отрицательных ω соответствующее выражение следует из соотношения B y ( x , m) = B y ( x , - m).

Ведущая асимптотика интеграла (17) определяется полюсом функции B_y ( x , ω), лежащим выше других в плоскости комплексного ω. Будем предполагать, что γ_{A n} << v_n . Такое предположение согласуется с оценками работы [Мазур, 2009]. Тогда наиболее важным оказывается полюс ω=ω A ( x )– i γ A n . К этому можно добавить, что роль полюсов ω=ω n – iv n уже изучена в предыдущем разделе. Учтем также, что вблизи точек альфвеновского резонанса x = x A n можно использовать разложение

I    x - '\ roA (x) = m„ 1--

A n

V      ² l An

Тогда асимптотику интеграла (17) можно представить в виде 1/2

B y ( x , t ) = - 8п У I ^V An ^{V w nl} A j x n V    ® n     J

% x---Сw(® n)   exp [-i ®A( x) t- YAnt ] ,           (19)

x - x_A - I £ l_A

An     n An где εn=2vn/ωn.

Поскольку в окрестности альфвеновского резонанса наиболее сингулярны функции B y и v y , то усредненная по координатам y и z плотность энергии колебаний (10) дается выражением

. lit, i2

W ( x , t ) = 1 R +

4  8n p°kyll

J

B_y ( x , t )²

16π

8π

V

Последнее равенство объясняется тем, что средние значения двух членов в круглой скобке равны друг другу. Подставляя сюда (19), получаем

W ( x , t ) =

= 4n 2 ^V A n ^{V w n} l A n    ।C ^w( ® ⁿ ) 2 exp( - 2YA, t ). (20)

„      CO      (x — xA ) + £ lA n         n              An       n An

Из выражений (19) и (20) видно, что возмущение представляет собой совокупность пиков, локализо- ванных вблизи точек альфвеновского резонанса, отвечающих собственным частотам магнитосферного резонатора: xAn=xA(ωn). Ширина каждого из этих пиков εnlAn~(vn/ωn)lAn определяется декрементом затухания соответствующей собственной моды резонатора vn, а скорость его затухания – декрементом затухания альфвеновской волны в точке соответствующего альфвеновского резонанса γAn.

Полная энергия, локализованная в окрестности n -го резонанса, получается интегрированием выражения (20) по некоторой окрестности точки x = x A n , размер которой много больше ширины соответствующего пика ε _nl _{A n} :

W A n = 2n^{2 V} A ^{n V w n}| C w n (O n )|² exp( - 2Y A t ).

A n           V      w n n            A n

n

Сравнивая с выражением (15), видим, что в область альфвеновского резонанса проникает (и затем диссипирует) доля энергии магнитосферного резонатора, равная

^W A n ^V An       ^V An

—— =--=------.

^W R n    ^V n    ^V An ^{+ V} w n

Излучение магнитосферного резонатора

Энергия магнитосферного резонатора не только поглощается в точках альфвеновского резонанса, но и утекает в солнечный ветер в виде убегающих волн. Чтобы исследовать этот эффект, необходимо учесть отличие коэффициента отражения от значения (–1). Это отличие существенно вблизи собственных частот резонатора. Согласно формуле (72) статьи [Мазур, 2009], близ этих частот

^R _w ^{( o )} = ^{- 1 +}

2 n

2 i V w n

® ^- ® n ^{+ i V} n

Первый член в этой формуле соответствует полному отражению волны, и его роль для нестационарных колебаний была рассмотрена выше. Второй член описывает временную асимптотику той части возмущения, которая поглощается магнитосферным резонатором и затем излучается обратно в солнечный ветер. Далее мы рассмотрим вклад только этого члена.

Обозначая соответствующую часть функции ς out ( x , t ) через ς_out( x , t ), из (9) имеем

?™t ⁽ x , t ) = 2 ^n, ⁽ x , t ),                               ⁽²²⁾

n

5n (x, t) = 4n [Po (x)cS (x)]1/2 Vw„

Излученное резонатором возмущение асимптотически представляет собой суперпозицию убегающих волн, имеющих частоты собственных мод резонатора.

Каждая из этих волн затухает по времени с декрементом vn, но экспоненциально растет по координате x по закону exp[vnτS(x)]. Такое поведение возмущения хорошо известно в квантовой механике, где оно возникает при рассмотрении распада мета-стабильного состояния [Ландау, Лифшиц, 2004]. Убегание энергии из резонатора через не полностью отражающую границу также, собственно, есть рас- пад метастабильного состояния. Указанная зависимость решения от координаты и времени диктуется законом сохранения энергии. Действительно, в солнечном ветре поток энергии волны связан с ее плотностью соотношением 5x = cSW, диссипация отсутствует, Q = 0 , следовательно, закон сохранения энергии (14) из статьи [Мазур, 2009] для отдельной волны из суперпозиции (22) можно записать в виде

• -2VnW +|-( cS W ) = 0.

дx

Отсюда получаем x 2V

W ~exP     /'//х = exP [VTS(x)] , xcs( x)

т. е. требуемое нарастание по координате x. Отметим, что на переднем фронте излученной волны, распространяющейся со скоростью c_S(x), где выполняется соотношение t–τ_S(x)=const, амплитуда волны постоянна – временное затухание компенсируется пространственным нарастанием.

Вычисляя по формуле (17) статьи [Мазур, 2009] поток энергии отдельной волны из суперпозиции (22), имеем

• ⁵xn =⁴ⁿ2^V Wn C(l'>n f exp {2^Vn [ ^TS⁽x)^-t ]}.

Полную энергию, излученную резонатором, можно получить интегрированием этого выражения по времени:

“                          2

Wwn = J 5n (xM, t) dt = 2n²-Wn ^7w(to n )| .

0                           ^Vn '

Сравнивая с (15), видим, что в солнечный ветер излучается доля энергии магнитосферного резонатора, равная

^WWn= ^V Wn WRn " Vn

^VWn

.

V An + VWn

Заключение

Сформулируем основные результаты работы.

• 1.    Падающее на магнитосферу ограниченное во времени волновое возмущение в основном отражается от магнитопаузы. Только сравнительно малая доля его энергии в узких спектральных диапазонах вблизи собственных частот магнитосферного резонатора ω=ω_n проникает в магнитосферу.

• 2.    Проникшая часть возмущения возбуждает собственные моды магнитосферного резонатора. Уровень возбуждения моды определяется спектральной плотностью падающих волн на частоте собственной моды C^%_W (ω_n ) . Эти моды затухают с декрементом затухания vn=vAn+vWn, который обусловлен двумя эффектами – поглощением энергии в окрестности альфвеновского резонанса и ее утека-нием через магнитопаузу в виде гидромагнитных волн назад в солнечный ветер.

• 3.    Каждая из возбужденных собственных мод формирует узкий пик возмущения, расположенный в глубине магнитосферы, в области непрозрачности собственной моды, в окрестности альфвеновского резонанса, соответствующего ее частоте: xAn=xA(ωn). Ширина каждого из этих пиков определяется декрементом затухания отвечающей ему моды: Δx_An=(2v_n/ω_n)l_An, а скорость его затухания – декрементом затухания альфвеновской волны в точке его локализации: γ_An=γ_A(x_An). Для типичных условий в магнитосфере γAn<<vn. Это означает, что возмущение в окрестности альфвеновских резонансов существует еще долго после того, как затухнут собственные моды резонатора. В окрестность альфвеновско-го резонанса проникает и затем диссипирует в ней доля энергии собственной моды, равная vAn/(vAn+vWn).

• 4.    Оставшаяся доля энергии, равная vWn/(vAn+vWn), уносится из резонатора убегающими в солнечный ветер гидромагнитными волнами. Эти волны излучаются резонатором на его собственных частотах ω_n и затухают с его декрементом затухания v_n. Это означает, что они излучаются длительное время после того, как отразится и убежит основной волновой пакет падающих волн.

Работа выполнена при поддержке РФФИ, гранты № 07-05-00185 и № 09-02-00082.