Возбуждение поверхностных плазмон-поляритонов наноантенной: простое аналитическое решение и его численная верификация

Поверхностные плазмон-поляритоны (ППП) представляют собой связанные колебания электромагнитного поля и поверхностной плотности заряда, распространяющиеся вдоль границы раздела между металлом (или высоколегированным полупроводником) и диэлектриком и эванесцентно затухающие в поперечных направлениях. Они впервые наблюдались экспериментально Р. Вудом в 1901 г. в виде аномалий в спектрах отражения металлических дифракционных решеток [1]. Правильную интерпретацию этим аномалиям дал У. Фано в 1941 г., связав их с возбуждением поверхностных волн, однако он не прояснил природу этих волн. Более детальное исследование поверхностных плазмон-поляритонных волн было выполнено позже Р. Ричи в работе [3].

Электромагнитное поле ППП, экспоненциально спадающее по мере удаления от границы, становится чрезвычайно локализованным вблизи резонансной частоты поверхностных плазменных колебаний (на которой действительная часть диэлектрической проницаемости металла равна –1). Это обуславливает перспективность применения плазмон-поляритонных волн для миниатюризации элементов интегральной оптики. В частности, плазмонные волноводы открывают возможность сжатия света на телекоммуникационных длинах волн до нанометровых масштабов

[4, 5]. Они используются, например, в области субволнового построения изображений [6] и в коммерчески доступных квантово-каскадных лазерах [7, 8]. Высокая пространственная локализация света в плазмонных структурах сопровождается гигантским усилением поля вблизи структур, что открывает широкие возможности в таких областях, как биосенсорика [9–11], нелинейная оптика [12–14], спектроскопия комбинационного рассеяния [15, 16] и усиление взаимодействия света с веществом [17–18]. Плазмон-поляритонные волны и колебания хорошо изучены как в сосредоточенных, так и в распределенных системах. Более подробные сведения о них можно найти во многих обзорах и монографиях [19–24].

Будучи поверхностной волной, ППП не могут быть возбуждены электромагнитной волной, падающей на поверхность металла из свободного пространства, из-за рассогласования фазовых скоростей. Как правило, для обеспечения фазового синхронизма между поверхностными плазмонами и падающим полем используются дифракционные решетки [25], призмы с высоким показателем преломления (схемы Отто и Кречмана) [26, 27] или дефекты, нарушающие трансляционную симметрию на поверхности металла (канавки, отверстия, выступы и др.) [28–30]. Альтернативным подходом является возбуждение ППП диэлектрическими или плазмонными наноантеннами [31–34]. Благодаря резонансным свойствам наноан- тенн, возбуждение ими поверхностных плазмон-поляритонов может быть весьма эффективным [35, 36]. Более того, интерференция между различными мультипольными моментами наноантенны позволяет динамически управлять направленностью возбуждаемых ППП [37], а также открывает возможность демультиплексирования плазмон-поляритонов на едином чипе [38].

Задача рассеяния плоской волны малой частицей на металлической подложке может быть решена аналитически в дипольном приближении с помощью формализма диадных функций Грина [39, 40]. Амплитуда возбуждаемой ППП волны может быть найдена путем вычисления остатка в полюсе френелевского коэффициента отражения. Этот метод дает хорошее согласие со строгим численным моделированием, но является математически громоздким и требует вычисления интегралов Зоммерфельда.

В данной работе предлагается простой альтернативный подход к вычислению вклада плазмон-поляритонной волны в полное поле рассеяния плазмонной наноантенны на металлической подложке. Данный метод основан на теореме взаимности [41 –43] и аналогичен известному в теории волноводов методу вычисления амплитуд мод, возбуждаемых источниками тока. Для наиболее наглядной демонстрации предлагаемого подхода мы рассмотрим простую двухмерную геометрию, в которой наноантенна представляет бесконечно длинный металлический цилиндрический стержень малого радиуса, расположенный параллельно поверхности металла. Сначала мы получим решение для случая, когда антенна имеет гармонически осциллирующий поперечный дипольный момент, заданный в явном виде. Затем мы рассмотрим возбуждение наноантенны отвесно падающей плоской волной, поляризованной перпендикулярно оси стержня. Полученные в обоих случаях аналитические результаты будут подтверждены численным моделированием методами конечных разностей и конечных элементов.

Возбуждение поверхностных плазмон-поляритонов источником с явно заданным дипольным моментом

Источник излучения в виде тонкого стержня поместим в вакууме на расстоянии x0 над поверхностью металлической пленки (рис. 1а). Пленку считаем достаточно толстой (значительно толще скин-слоя, который для благородных металлов в видимой и ближней инфракрасной области спектра имеет толщину ~15 нм), чтобы поверхностные плазмон-поляритоны возбуждались только на верхней поверхности плёнки. Стержень неограниченно вытянут вдоль оси y (она направлена на наблюдателя на рис. 1), при этом дипольный момент на единицу длины стержня будем считать заданным и равным p0 / l, где вектор дипольного момента p0 параллелен оси z и неявно включает в себя временную зависимость вида exp(– iωt). Если диаметр стержня считать бесконечно малым, плотность тока в стержне может быть записана как J = iωp0l –1δ (x – x0) δ (z). Для расчета эффективности возбуждения таким током плазмон-поляритонных волн на поверхности пленки воспользуемся выражением, следующим из несопряженной теоремы взаимности [41]:

1 a =-          e ⋅ J e ^{- i β z} dV.

4 N C ^{( V )}

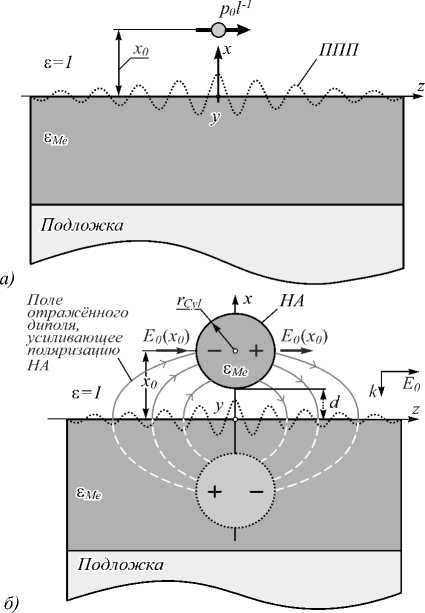
Рис.1. Возбуждение ППП в металлической плёнке: «точечным» 2D-диполем. Величина дипольного момента единицы длины стержня p 0 l ^-1 задаётся условиями задачи и не зависит от внешних факторов (а); цилиндрической наноантенной (б). На цилиндрический стержень воздействует поле суммарной (отвесно падающая + отражённая) волны E 0 и поле отражённых в плёнке зарядов

В этом соотношении β и N C =(1 /2) | ∫ S e × h ⋅ n z d S | – постоянная распространения и нормировка моды соответственно; n z – единичный вектор в направлении оси z ; e , h – распределение векторов электрического и магнитного поля моды в поперечном сечении ( S ) волновода соответственно; V – объем, занимаемый источниками тока. Вообще говоря, выражение (1) связывает эффективность возбуждения моды ( a ) в диэлектрическом оптическом волноводе с плотностью возбуждающего её тока ( J ). Но при его выводе не использовалось никаких ограничений на проводимость среды [41], что дает основания обобщить его на случай плазмонных волноводов.

Компоненты векторов e , h и другие необходимые для вычислений параметры плазмон-поляритонной волны записываются, как [19]:

e z = iA У vac ■ X о ( x )( ®S q ) 1 ,

X 0 ( x ) =

e x = - A 3- X о ( x ) n = ( x )( ®S q ) 1 , h y = A ■ X о ( x ) , e y = h_x = h_z = 0, exp( -y vac x ), x >  0 exp( y Me x ), x <  0 , [ 1, x >  0

nJ x ) =              ,

^E( ) [ 1/ £ Me , x <  0

^Y Vac    ik (^£ Me + 1 ) ,

^Y Me    ik ^£ Me (^£ Me

- 1/2

P = k(бMe / (бMe +1))1/2, где A – произвольная константа размерности А / м. В нашем случае, когда «точечный» ток колеблется вдоль оси z, интегрирование выражения (1) дает top 0

a = -     У Vac

Al

£

3/2 Me

^£ Me + ¹

e ^Y Vac x 0

Распределение компонент напряженности электрического ( E SPP = a ■ e ) и магнитного ( H S^PP = a ■ h ) полей возбуждённой плазмон-поляритонной волны удобно представить в виде E ^SPP = E 0PP X ₀ ( x ) e ^- ' ^e z и H SPP = h spP X ₀ ( x ) e ^{- i} P z соответственно, где индекс i последовательно пробегает значения x, y, z, а коэффициенты E ₀ ^S _i ^PP и H ₀ ^S _i ^PP также соответственно представляют амплитуды электрического и магнитного полей ППП. Например, ненулевые z - и x -компоненты амплитуды электрического поля, с учетом найденного выше выражения для параметра a , записываются как:

E 0PP =— P 0 1 ^{-1 l Va £} 0

^£ Me + ¹

e У Vac x 0

E SPP

^{0 x} x =± 0

=-V£ Me n £ ( ± 0 ) p 0 1 ^{1 Y} V^ac- £ 0

3/2

^£ Me

^£ Me ^{+ 1}

e ^y Vac x 0

На рис. 2 представлены расчеты зависимости компоненты E 0 ^Sz^PP от длины волны источника для случая золотой пленки, p 0 l ^–1 = 10 ^–24 Кл и различных значений x 0 (сплошные кривые). Данные о дисперсии комплексной диэлектрической проницаемости золота взяты из справочника CRC [45].

Численное исследование процессов возбуждения ППП точечным двухмерным дипольным источником проводилось методом конечных разностей во временной области с использованием программного пакета Lumerical FDTD. Размеры ячейки расчетной сетки и всей области расчета выбирались так, чтобы они не влияли на результаты расчета. На границах обла- сти расчета использовались поглощающие граничные условия типа «perfectly matched layer» (PML). Спектральный диапазон для расчетов выбирался в видимой (и ближней ИК) части спектра в диапазоне длин волн от 400 до 700 нм.

0,6

0,5

0,4

0,3

0,2

0,1

а)

б)

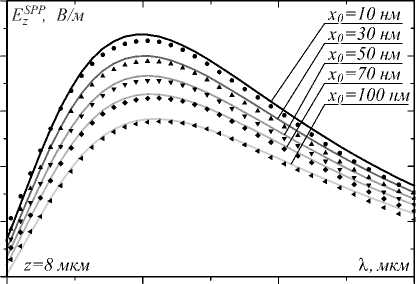
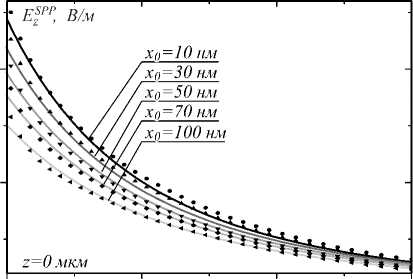
Рис. 2. Сравнение численных (точки) и аналитических (сплошные кривые) результатов расчёта амплитуды продольной компоненты поля ППП на поверхности металла (x = 0) на удалении 8 мкм (а) и 0 мкм (б) от начала координат, расположенного непосредственно под дипольным источником, для различных значений высоты x 0 источника над плёнкой. Результаты, представленные на рис. 2б, получены при помощи экстраполяции. Максимум всех кривых на первом рисунке обусловлен тем, что по мере распространения «коротковолновые» ППП ослабляются значительно сильнее, чем «длинноволновые»

Получаемое в результате моделирования распределение электромагнитного поля является результатом суперпозиции ближнего поля дипольного источника, поля его излучения и поверхностной плазмон-поляритонной волны. Можно предположить, что во всем расчетном спектральном диапазоне амплитуды первых двух составляющих будут быстро спадать с удалением от источника. В то же время в длинноволновой части спектра, характеризующейся сравнительно низкими потерями ППП [19], амплитуда плаз-мон-поляритонной волны останется достаточно высокой и на значительном удалении от источника. Это иллюстрируется распределением амплитуды суммарного электрического поля, рассчитанным на длине волны X = 650 нм, в котором отчетливо видна возбуждаемая плазмон-поляритонная волна, локализованная вблизи поверхности металла (рис. 3а). Расчеты такого распределения на различных длинах волн показывают, что зависимость амплитуды продольной компоненты электрического поля от координаты z приобретает на поверхности металла (при x =0) чисто экспоненциальный характер при выполнении условий z > 8 мкм и X> 550 нм. Причем коэффициент затухания такой экспоненты в точности задается мнимой частью постоянной распространения ППП р. Это доказывает, что при названных выше условиях на поверхности металлической пленки в суммарном поле доминирует плазмон-поляритонная волна, что даёт возможность оценить её амплитуду в удаленной точке, а также ее начальную амплитуду путем экстраполяции из этой точки в начало координат (z =0, x =0) с учетом известного экспоненциального закона затухания амплитуды ППП [19]. Процедура такой экстраполяции иллюстрируется рис. 3б, на котором сплошной кривой показана амплитуда продольной компоненты электрического поля на поверхности металла (в логарифмическом масштабе), рассчитанная на длине волны X = 577 нм, а также пунктирной линией обозначен закон затухания амплитуды ППП на данной длине волны (Im(P)/kO = O,O127).

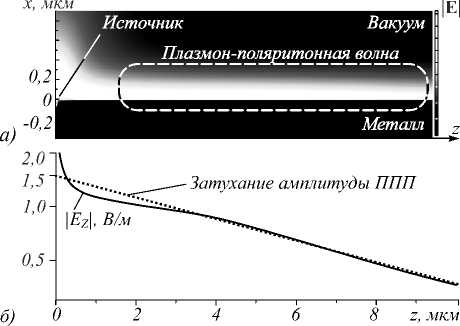
Рис. 3. Численно рассчитанное распределение амплитуды электрического поля дипольного источника, расположенного непосредственно над поверхностью металла, на длине волны А = 650 нм (а), а также зависимость амплитуды продольной компоненты электрического поля на поверхности металла от координаты z на длине волны А = 577нм и экстраполяция амплитуды возбуждаемой ППП волны в начало координат для нахождения её исходной амплитуды (б)

Результаты численных расчетов зависимости z-компоненты амплитуды электрического поля плаз-мон-поляритонной волны от длины волны возбуждающего её источника представлены точками на рис. 2. При этом данные рис. 2а соответствуют случаю, когда амплитуда регистрируется в точке с координатами z =8 мкм, x =0, а на рис. 2б – случаю, когда она регистрируется в начале координат, расположенном на поверхности металлической пленки под источником (z =0, x =0). Непосредственное сравнение аналитической и численной зависимостей реализуется на рис. 2а. На рис. 2б сравнивается аналитическая кри- вая и результат экстраполяции численных данных в начало координат. На обоих рисунках видно хорошее соответствие аналитических и численных зависимостей, что подтверждает справедливость используемого подхода для аналитического расчета амплитуды ППП.

Возбуждение поверхностных плазмон-поляритонов наноантенной, освещаемой отвесно падающей плоской волной

Рассмотрим теперь случай возбуждения ППП цилиндрической наноантеной (НА) в виде тонкого и очень длинного металлического стержня круглого сечения ( r_Cy1<<  X , 1_Cy1 >>  X , где r_Cy1 и 1_Cy1 - соответственно радиус и длина стержня, X - длина волны освещения), помещенного на расстоянии x 0 над поверхностью пленки из того же металла, так что между пленкой и наноантенной образуется зазор d = x 0 – r Cyl (рис. 1 б ).

Наноантенна освещается плоской электромагнитной волной, отвесно падающей на поверхность пленки. В отсутствие НА вклад в электромагнитное поле над поверхностью пленки ( x >  0) вносит отраженная волна, так что напряженность электрической компоненты E 0 ( x ) суммарного поля запишется как E o ( x )= E o i ( e ^- ikx + re ^{- ikx} ), где r = (1 -JZ Me ) / (1 + JZ M _e ) -френелевский коэффициент отражения от поверхности металла, s Me - диэлектрическая проницаемость материала пленки, внутри же металлической пленки ( x < 0) эта напр яже нность равна E _o ( x ) = t E _o i e - i^k^e^x , где t = 2/(1 + ^ m _M e ) - френелевский коэффициент пропускания границы раздела металл-вакуум (множитель e ^- i ^m t в приведенных выражениях и далее подразумевается, но явно не приводится). Цилиндрическая НА вносит изменения в распределение первичного электрического поля вследствие поляризации её материала. Если бы не влияние подложки (surface dressing effect), то в рамках электростатического приближения, которое справедливо для стержня малого радиуса, под действием первичного поля E 0 ( x ) НА приобретала бы дипольный момент (ДМ), равный:

pCy1 = 2Vcyiso (sMe —1) Eo (xo) / (sMe +1), где VCy1 = nrC:yi1Cy,i - объём цилиндра. Чтобы пояснить влияние подложки [39], представим для простоты разделенные в стержне поляризационные заряды как точечные (точнее в 2D-геометрии – это длинные тонкие заряженные нити). Оба таких заряда отражаются в металлической пленке, причем отраженные заряды формируют вокруг себя неоднородное электрическое поле (рис. 1б), под действием которого исходная цилиндрическая НА приобретает как дополнительный дипольный, так и мультипольные моменты различных порядков. Величина приобретенного НА дополнительного ДМ будет равна PCyl = qcPoyl, где qc=((sMe-1)rcyl/(2 (sMe+1)xo))2. С дипольным моментом p1Cyl можно связать дополни- тельные поляризационные заряды в НА, которые затем вновь отразятся в пленке и индуцируют новый дополнительный вклад в ДМ наноантенны, и так до бесконечности. После суммирования соответствующей геометрической прогрессии результирующий дипольный момент НА можно найти в виде:

p Cyl = F ACy p Cyl , (3)

где F CC = 1/(1 - q_C ) - фактор усиления дипольного момента из-за влияния отражения в пленке. Следует отметить, что точность выражения (3) будет снижаться при малом зазоре между цилиндром и поверхностью пленки ( d <<  r Cyl ), поскольку в этом случае на величину дипольного момента НА будут влиять отраженные мультиполи высших порядков, однако для простоты мы пренебрежем этим влиянием. Упрощая задачу далее, заменим наноантенну точечным 2D-диполем с амплитудой колебаний дипольного момента, задаваемым выражением (3). Тогда амплитуда возбуждаемой наноантенной ППП волны может быть получена просто при замене величины p 0 на p^Cyl в соотношениях (2). В частности, для z -компоненты амплитуды ППП на границе металла с вакуумом имеем:

SPP 2

E 0 z =  У Vac

3/2

⁶ Me

S Me + ¹

2 n A

⁶ Me ¹

6 Me + 1

X

X F C exp ( -Y vac X 0 ) E о ( x о ) .

0     0,04 0,08 0,12 0,16 0,20 0,24 d.MKM

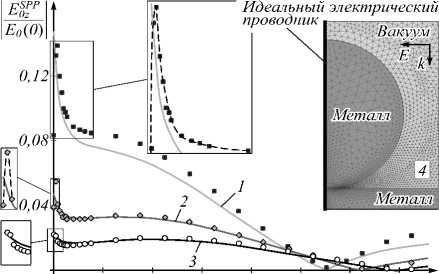
Рис. 4. Результаты расчётов зависимости амплитуды продольной компоненты электрического поля ППП, нормированной на амплитуду E 0 (0) первичной волны на границе раздела плёнка-вакуум, от ширины зазора между цилиндрической НА и плёнкой. Сплошные кривые – результат аналитических расчётов для случая r Cyl = 20 нм и A = 550 нм (1), A = 600 нм (2), A = 650 нм (3). Точками представлены численные результаты. Чтобы подчеркнуть различие характера аналитических и численных результатов на начальном участке зависимостей 1 и 2, эти участки представлены на вставках в увеличенном масштабе, причём численные результаты на этих вставках интерполированы пунктирными линиями.

На вставке 4 показана неравномерная расчётная сетка для численного решения задачи методом конечных элементов с использованием программного пакета COMSOL Multiphysics

Результаты расчетов амплитуды этой компоненты в зависимости от ширины зазора d между пленкой и

цилиндрической НА показаны на рис. 4, в зависимости от радиуса наноантенны r Cyl – на рис. 5 и в зависимости от длины волны X - на рис. 6.

На рис. 4–6 сплошные кривые – результат аналитических расчетов в соответствии с выражением 4, точками представлены численные результаты. Применение метода конечных разностей во временной области для численного моделирования возбуждения ППП малой наноантенной круглого сечения оказывается малоэффективным в связи с трудностью разрешения скругленной поверхности НА, а также зазора между НА и поверхностью металла прямоугольной сеткой, используемой в методе FDTD. Поэтому в данном случае численные расчеты выполнялись методом конечных элементов в частотной области (FEFD) с использованием программного пакета COMSOL Multiphysics. Для обеспечения сходимости численных результатов применялась неравномерная сетка с уменьшением размера элемента в области зазора между поверхностью металла и НА (вставка 4 на рис. 4). С учетом симметрии рассматриваемой геометрии моделировалась ее половина с граничным условием «идеальный электрический проводник» (PEC) на вертикальной линии симметрии.

Видно, что все аналитические зависимости E 0 ^Sz^PP ( d ) на рис. 4 показывают резкое снижение амплитуды ППП на начальном участке кривых, в то время как численные расчеты, выполненные для X = 550 нм и X = 600 нм, демонстрируют сначала очень быстрое возрастание амплитуды (когда зазор не превышает соответственно ~3 нм и ~1,5 нм, что проиллюстрировано вставками на рис. 4) и лишь затем её снижение. Это различие объясняется влиянием высших мультипольных моментов, которые не учитываются в аналитических расчетах. Влияние мультиполей является очень «короткодействующим», поэтому оно проявляется только при самых минимальных зазорах, а затем, как видно из рис. 4, аналитические и численные результаты практически совпадают. Отсутствие различий на начальном участке аналитической и численной зависимостей при X = 650 нм (кривая 3) объясняется следующими соображениями. Действительно, эффективность возбуждения высших локальных плазмонных мод в НА (квадрупольной, октопольной и т.д) обычно резко падает с увеличением отношения длина волны / радиус наночастицы [46]. Вследствие этого влияние мультипольных моментов проявляется только для «коротковолновых» зависимостей 1 и 2 и не заметно для более «длинноволновой» зависимости 3. Дальнейшее резкое уменьшение амплитуды ППП с ростом ширины зазора для всех расчетных длин волн объясняется быстрым ослаблением влияния отраженных в пленке зарядов на дипольный момент НА, пока последний по достижении некоторого порога не принимает значения, примерно равного дипольному моменту тонкого стержня в вакууме (в выражении (3) фактор усиления F_A ^Cyl быстро уменьшается с ростом величины зазора и становится почти

равным единице, при d ~ 8 нм (при λ =650 нм), 10 нм ( λ =600 нм) и 14 нм ( λ =550 нм)). Затем падение амплитуды плазмонной волны существенно замедляется (кривая 1 на рис. 4) или может даже смениться незначительным ростом (кривые 2, 3). Далее характер зависимости E ₀ ^S _z ^PP ( d ) может быть описан как некоторая квазиперио-дическая, постепенно затухающая функция. Такое поведение объясняется тем, что, с одной стороны, наноантенна последовательно попадает в пучности и узлы первичного поля E 0 (периодичность), а с другой – её влияние на электронную плазму приповерхностного слоя пленки снижается с удалением от пленки по закону exp(– γ Vac x 0 ) (затухание).

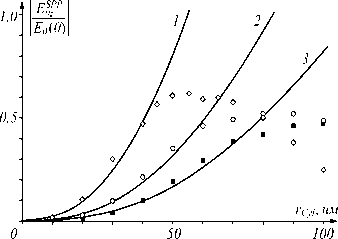
Рис. 5. Результаты расчётов зависимости начальной амплитуды продольной компоненты электрического поля ППП, нормированной на амплитуду E 0 (0) первичной волны на границе раздела плёнка-вакуум, от радиуса цилиндрической НА. Сплошные кривые – результат аналитических расчётов для случая d = 10 нм и λ = 550 нм (1), λ = 600 нм (2), λ = 650 нм (3). Точками представлены численные результаты

Расчеты зависимости начальной амплитуды ППП от радиуса цилиндрической наноантенны (рис. 5) проводились для случая, когда между НА и плёнкой поддерживается постоянный зазор шириной 10 нм. Последнее было сделано, чтобы избежать влияния мультиполей высоких порядков на результаты численного счета. Из представленных результатов видно, что квадратичный рост амплитуды ППП, предполагаемый на основании выражения 2, подтверждается результатами численного расчета, пока радиус НА не превышает ~50 нм. Существенные различия при большем радиусе, несомненно, являются следствием ограниченности применимости квазистатического приближения.

Расчет зависимости начальной амплитуды ППП от длины освещающей наноантенну волны (рис. 6) также выполнялся для случая, когда между НА и плёнкой имеется зазор шириной 10 нм, позволяющий не принимать во внимание влияние мультиполей. Нижняя граница спектрального диапазона для численных расчетов составила 550 нм, что обсуждалось выше. Для аналитических же расчетов она выбрана равной 490 нм так, чтобы вещественная часть диэлектрической проницаемости золота была меньше минус единицы во всем расчетном диапазоне. Последнее, собственно, является условием эффективного возбуждения ППП на границе раздела золото-вакуум [44]. Верхняя граница расчетного диапазона выбиралась так, чтобы она оставалась в видимой области спектра. Из представленных на рис. 6 результатов аналитического расчета следует, что при rCyl =20 нм максимальная амплитуда возбуждения ППП достигается на длине волны λ ~512 нм, что приблизительно на 5 нм больше длины волны дипольного резонанса тонкого золотого стержня в вакууме, положение которого задается максимумом величины p0Cyl . Это отличие скорее всего связано с влиянием подложки, а не с эффектами запаздывания поля, поскольку последние, как это следует из данных, представленных на рис. 5, проявляются слабо для цилиндра столь малого радиуса. Из рис. 6 также видно, что в пределах спектральной области, для которой выполнялся численный расчет, полученная в результате зависимость хорошо согласуется с аналитической кривой. Численные расчеты полностью подтверждают справедливость используемого аналитического подхода.

Мы полагаем, что полученные результаты вполне обосновывают применимость предлагаемого простого подхода к задаче о возбуждении плазмон-поляритонных волн дипольным источником, который в дальнейшем может быть полезен, для моделирования различных явлений, связанных с возбуждением ППП в плазмонике, микро- и нанооптике. Следует, однако, иметь в виду, что наше рассмотрение касается металлической наноантенны в простейшей 2D-геометрии. Тем не менее, предлагаемый подход применим для решения задачи о возбуждении плазмон-поляритонов дипольной наноантенной с произвольной диэлектрической проницаемостью, а также в полной трехмерной геометрии, что мы планируем показать в следующей статье.

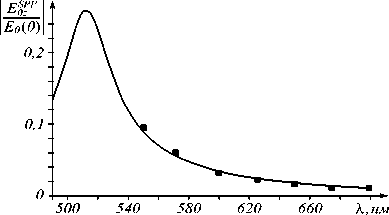
Рис. 6. Результаты расчётов зависимости начальной амплитуды продольной компоненты электрического поля ППП, нормированной на амплитуду E 0 (0) первичной волны на границе раздела плёнка-вакуум, от длины освещающей

НА плоской волны. Сплошная кривая – результат аналитических расчётов для случая d = 10 нм и r Cyl = 20 нм.

Точками представлены численные результаты

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант №20-02-00556А).