Воздействие высокоскоростных частиц техногенного космического мусора на сложные технические объекты и их элементы

Аварийные ситуации сложных технических объектов (СТО) на орбите связаны с проблемой техногенного космического мусора [1–3] и весьма актуальны в последнее десятилетие. Столкновения высокоскоростных частиц космического мусора с СТО могут вызывать как локальные, так и глобальные их повреждения. Вторичные частицы, возникающие при разрушении СТО, могут приводить, например, к пробою труб контура теплоносителя или каналов защиты систем управления СТО. Ниже рассмотрены процессы высокоскоростного воздействия частиц техногенного мусора на СТО и его элементы на примере пробития многослойной разнесенной трубы сплошной и полой частицей.

Постановка задачи

Следуя [4; 5], будем использовать модель твердого деформируемого тела, которая состоит из уравнений баланса массы, импульса и энергии, а также уравнений состояния и упруго-пластического течения: ■

* i = u i;

уравнение неразрывности среды

Vo-Ро = V- р;

закон изменения импульса материальной частицы

о • и = с ; Р 1 У , j ;

изменение внутренней энергии частицы

Р-e = ст j-sj тензор скоростей деформаций имеет вид s у = 0,5 • (ui, j + uj, i);

тензор напряжений представим в общепринятой форме ij

-5 _Zj • P + s j ,

где s ij - девиатор тензора напряжений, отвечающий за реакцию на сдвиговое формоизменение материальной частицы; δ _ij – символ Кронекера; P – функция давления в форме Ми – Грюнайзена.

Уравнения процесса принимаем в форме Прандтля – Рейсса

sj + d!‘• sj = 2• G•£j, sj =sj-skk/3, при условии пластичности Губера – Мизеса sj- s^ 2 • Y0/3, где Y0 – динамический предел текучести, а для определения скалярного множителя dX' используется известная процедура приведения к кругу текучести. В приведенных выше уравнениях использованы общепринятые обозначения: каждый из индексов i, j пробегает значения 1, 2; по повторяющимся индексам проводится суммирование; точка над символом – производная по времени; индекс после запятой - производная по соответствующей координате; xi, ui - компоненты векторов положения и скорости материальной частицы соответственно; р - текущая плотность; G - модуль сдвига.

Уравнения в частных производных преобразуются в явную разностную схему на треугольной сетке вдоль траектории каждой материальной частицы (в данном случае - ячейка разностной сетки).

Для учета процессов разрушения система дополняется соотношениями, связывающими параметры напряженно-деформированного состояния с предельными величинами материалов [5; 6]. В качестве уравнения состояния используется термодинамически полное малопараметрическое уравнение состояния [7; 8], которое отличается тем, что практически все параметры можно найти в справочниках по физико-механическим свойствам материалов. Разностная сетка в сложных многосвязных областях строится динамическим способом [9; 10]. Расчет контактных поверхностей между взаимодействующими деформируемыми твердыми телами осуществляется по симметричному алгоритму [11]. Упомянутые выше разработки реализованы в виде комплекса программ REACTOR 2D, позволяющего решать плоские и аксиально-симметричные задачи механики деформируемого твердого тела в широком диапазоне скоростей встречи [12].

Результаты моделирования. Рассмотрим процесс высокоскоростного взаимодействия налетающего тела с модельным сложным техническим объектом.

На рис. 1 представлена геометрическая модель СТО в плоской постановке (момент времени

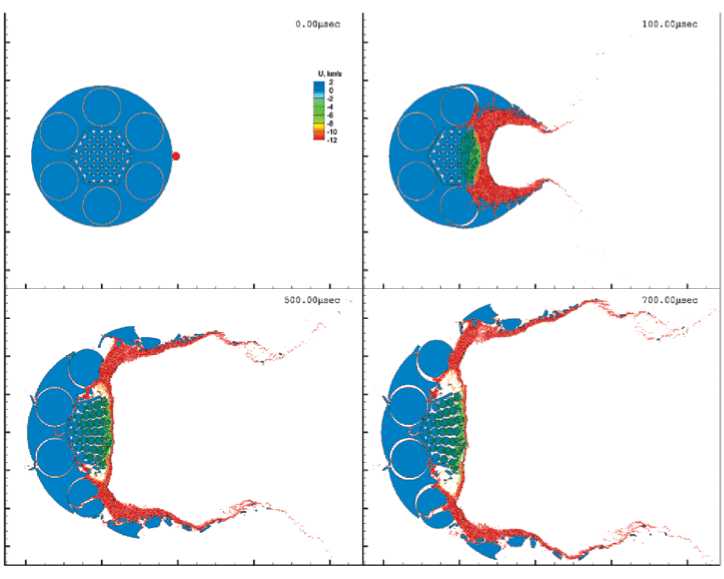
Рис. 1. Кинограмма процесса деформирования и разрушения СТО под действием частицы техногенного космического мусора

U ИССЛЕДОВАНИЯ плуко____________

■ ГРАДА t = 0 мкс). Состав модельного СТО: бериллиевая оболочка с цилиндрическими вставками из того же материала с малым зазором; шестиугольная стальная камера, наполненная цилиндрическими объектами из UO2. На СТО налетает частица диаметром 2 см из алюминия со скоростью 11,7 км/с. От поверхности контакта взаимодействующих тел в обе стороны распространяется сильная волна сжатия. Поскольку волна сжатия на пути распространения встречает границы тел, причем имеющие зазоры, то формируется сложная картина взаимодействий волн нагрузки и разгрузки. Так 8     же образуются волны разгрузки от различных сво бодных поверхностей, что формирует зоны с растягивающими напряжениями, и при достижении критических значений растягивающих напряжений происходит разрушение материала отрывом.

За фронтом сжимающих напряжений частицы материалов приходят в движение относительно друг друга, т.е. начинается процесс накопления деформаций и при достижении критических значений главных растягивающих и сдвиговых деформаций также происходит разрушение материала. Поскольку область первоначальной встречи налетающего тела и модельного СТО подвержена максимальным нагрузкам, а следовательно, и деформациям, то она получила и максимальное разрушение (рис. 1, момент времени t = 700 мкс), причем боковые волны разгрузки разметали фраг- менты разрушенного материала из этой области в разные стороны от налетающей частицы.

В процессе разрушения СТО высокоскоростной частицей КМ образуются многочисленные фрагменты. Рассмотрим процесс пробития многослойного стального трубопровода сплошной и полой сферическими частицами при скорости столкновения 4,5 км/с.

На рис. 2 приведена кинограмма процесса взаимодействия сплошной алюминиевой сферы диаметром 0,2 см со стальной многослойной, разнесенной трубой (труба в трубе). Диаметры труб – 13,0 см, 11,0 см и 9,0 см. Толщина труб – внешние по 0,05 см, внутренняя – 0,15 см. Зазоры – 1,0 см.

Пробив первую трубу - экран, частица полностью фрагментирована, угол конуса разлета близок к 90 градусам. Центральная часть облака имеет несколько меньшую скорость по отношению к периферии, но содержит самые крупные фрагменты [13]. Центральная часть облака осколков пробивает и вторую трубу, но при этом теряет как свою массу, так и скорость (момент времени t = 10,0 мкс). Запреградное облако осколков уже не способно пробить последнюю, более толстую трубу, преодолев примерно две трети ее толщины. В дальнейшем подходящие следом осколки не смогли преодолеть оставшуюся треть толщины внутренней трубы, расчет продолжался до момента времени t = 80,0 мкс.

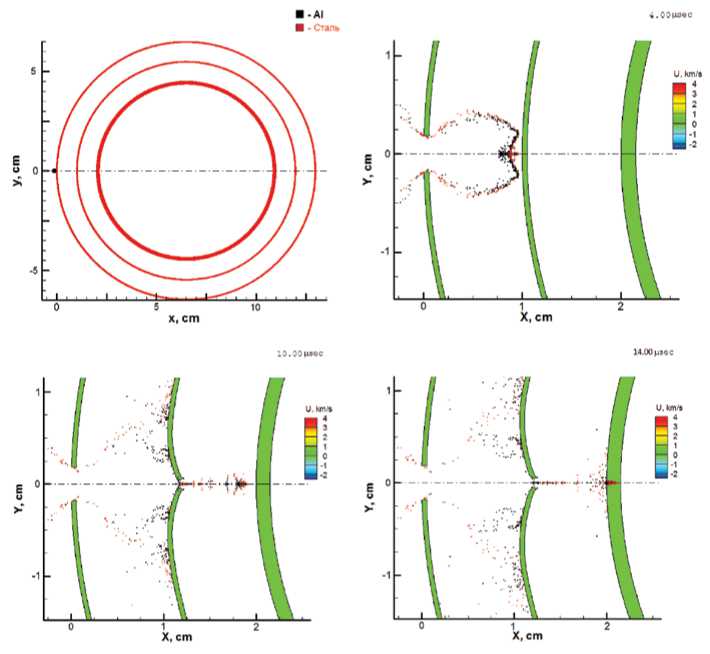
Рис. 2. Временные кадры результатов расчета процесса пробития сплошной алюминиевой сферой многослойной стальной трубы при скорости 4,5 км/с

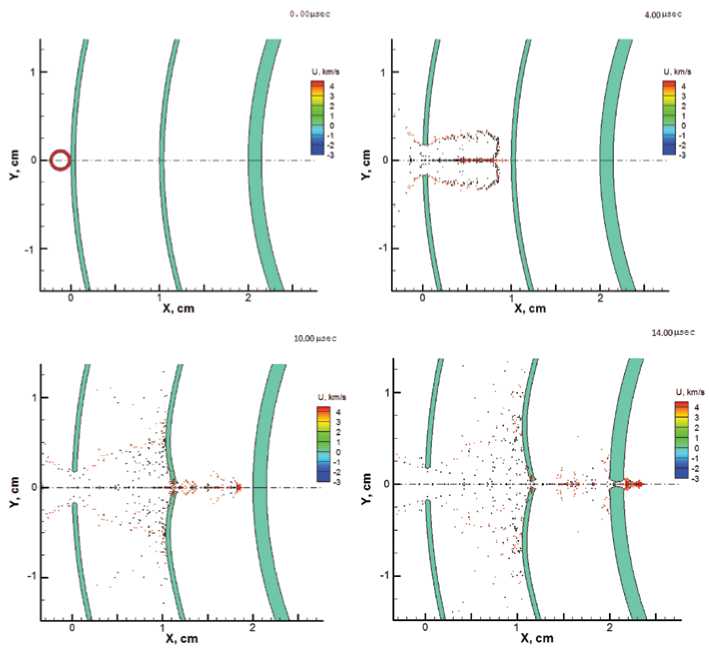
Рис. 3. Кинограмма процесса взаимодействия полой алюминиевой сферы с многослойной стальной трубой

Если взять полую алюминиевую сферу той же массы, как и в предыдущем расчете (диаметр – 0,24 см, толщина стенки – 0,06 см, рис. 3, t = 0,0 мкс), то за счет разнесения массы удается сформировать более устойчивую конфигурацию в центре осколочного облака, причем угол конуса разброса фрагментов примерно 60 градусов (рис. 3, t = 4,0 мкс).

Стенка второй трубы отсекает периферию облака осколков, но центральная часть облака за счет большей концентрации фрагментов и меньшей потери скорости пробивает ее (рис. 3, момент времени t = 10,0 мкс). В дальнейшем и внутренняя труба оказалось пробита. Таким образом, вторичные полые осколки представляют собой большую опасность для внутренних систем СТО, несмотря на их относительно более низкую скорость.