Возможность применения к космическим системам стохастических сетей Петри для анализа живучести

Моделирование, анализ и прогнозирование отказов находятся в центре внимания многих технических дисциплин, занимающихся проектированием и эксплуатацией инженерных систем, таких как аэрокосмическая промышленность и электротехника. В связи с этим возникают две задачи:

• 1.    Оценить и ранжировать различные варианты проектирования на основе их склонности и способности справляться с отказами.

• 2.    Выбрать конструкцию, которая предотвратила бы возникновение или уменьшила склонность системы к сбоям, смягчила или сдержала последствия сбоев, если они происходят, обеспечила своевременное и эффективное восстановление после сбоев.

Учитывая проектирование и разработку сетевых систем, становится еще более важным умение оценивать склонность к отказам сетевых систем, будут ли они испытывать катастрофические сбои или постепенную деградацию, например, после отказа узла или компонента (распространение сбоев по всей системе независимо от того, вызвано ли это эндогенными или экзогенными причинами). Исследуется применимость стохастических

Брусков Артем Алексеевич аспирант. Технологический университет имени дважды Героя Советского Союза летчика-космонавта А.А. Леонова, город Королёв. Сфера научных интересов: системный анализ, управление и обработка информации. Автор 9 опубликованных научных работ.

сетей Петри (далее – ССП) к анализу отказов и живучести в нескольких состояниях с использованием в качестве примеров космических систем.

Сети Петри

Сети Петри были предложены в 1962 году немецким ученым Карлом Адамом Петри (1926–2010). Сеть Петри – это двудольный ориентированный граф, используемый для моделирования систем с дискретными событиями, которые могут отображать параллельные или асинхронные процессы. Граф сети Петри имеет 2 непересекающихся набора вершин (или узлов) – позиции и переходы. Направленные дуги рисуются между позицией и переходом (входной дугой) или, наоборот, между переходом и позицией (выходной дугой). Позиции, соединенные с переходом входными дугами, называются входными позициями этого перехода, и наоборот, позиции, соединенные с переходом выходными дугами, называются выходными позициями этого перехода. В дополнение к позициям, переходам и направленным дугам сети Петри также имеют маркеры, или метки, которые могут быть связаны с каждой позицией, переходом или дугой [10].

Чтобы лучше понять конструкцию и эволюцию сети Петри, рассмотрим следующий пример. Система состоит из двух подсистем; каждая из них может находиться в двух состояниях – работоспособном или отказавшем. После сбоя каждая подсистема может быть восстановлена и возвращена в рабочее состояние, но только по одной подсистеме за один раз. Другими словами, одновременно может быть восстановлена только одна подсистема. Эта система показана на Рисунке 1.

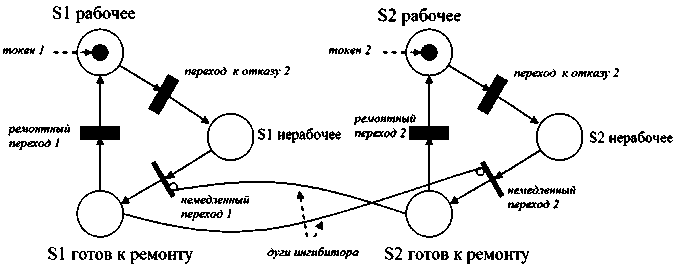
Рисунок 1. Система с очередью на ремонт (начальная конфигурация с подсистемой 1 ( S 1) и подсистемой 2 ( S 2), системы первоначально в рабочем состоянии)

Немедленные переходы могут быть переопределены дугами-ингибиторами, чтобы гарантировать, что одновременно восстанавливается только одна подсистема; например, если подсистема 1 ( S 1) выходит из строя первой, маркер 1, первоначально находя-

Возможность применения к космическим системам стохастических сетей Петри ...

щийся на месте с надписью « S 1 работает», переходит на место с надписью « S 1 сбой», и поскольку подсистема 2 все еще работает, включается немедленный переход, и маркер 1 переходит в место с надписью « S 1 готов к ремонту». Поскольку теперь в этом месте присутствует маркер, дуга ингибитора переопределяет немедленный переход 2. Как следствие, если подсистема 2 выходит из строя, в то время как непосредственный переход 2 все еще заблокирован, маркер 2 останется на месте с надписью « S 2 сбой» до тех пор, пока маркер 1 не перейдет обратно на место с надписью « S 1 работает». В этом примере вместо дуг-ингибиторов можно было бы использовать дуги-включения: дуга включения между « S 1 работает» и непосредственным переходом 2, и дуга между « S 2 работает» и непосредственным переходом 1 смоделировала бы то же поведение.

Стохастические сети Петри для моделирования отказов и живучести

Анализ и моделирование отказов в нескольких состояниях. Можем предположить, что ССП имеют ряд преимуществ перед цепями Маркова для моделирования и анализа систем с несколькими состояниями. Один из аргументов в поддержку этого утверждения следующий. Рассмотрим систему, которая состоит из k подсистем, и каждая подсистема может находиться в m разных состояниях. В случае моделирования сети Петри для моделирования эволюции состояния этой системы необходимы только позиции km (наличие маркеров в позициях будет отражать, в каком состоянии находится система). При марковском подходе необходимы состояния mk .

На Рисунке 2 показано соотношение числа состояний по отношению к числу подсистем (позиций) k и для 4 различных значений числа состояний на подсистему m (от m = 2 для нижней кривой до m = 5 для верхней кривой), требуемых для использования сети Петри.

Рисунок нанесен на график с логарифмической осью y из-за резкого увеличения этого соотношения для более высоких значений k и m .

Рисунок 2 выглядит следующим образом. Например, для k = 5 и m = 5 (самая верхняя кривая) модель Маркова требует на 125 состояний больше, чем позиций в модели сети Петри. Распространение состояний, или позиций, когда k или m увеличиваются, является сложной задачей для анализа сбоев в нескольких состояниях, но значительно более легкой, чем в случае марковского подхода.

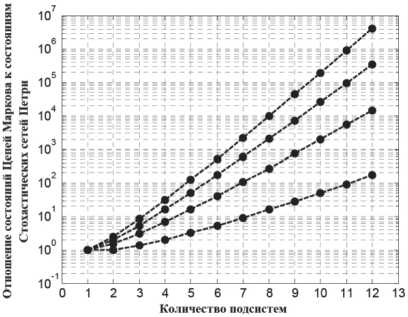
Рисунок 2. Разница в количестве состояний в цепях Маркова по сравнению с сетями Петри (нижняя кривая представляет подсистемы с 2 состояниями, а верхняя кривая – с 5 состояниями)

На Рисунке 2 также показано, что для систем с семью или более компонентами даже в случае традиционного бинарного анализа надежности цепи Маркова требуют на порядок больше состояний для моделирования системы, чем позиций в эквивалентной сети Петри [6]. Эта особенность цепей Маркова вытекает из того факта, что марковское моделирование требует «глобальных состояний» и «глобальных часов» для системы, чтобы запустить эволюцию состояний. То есть система может находиться только в одном состоянии одновременно, и это состояние описывает состояние всех подсистем, эволюционирующих во времени относительно уникального «глобального» времени. Напротив, сети Петри допускают локальное моделирование позиций для каждой подсистемы и локальное время, где каждая подсистема развивается со своим собственным маркером (маркерами), а состояние системы определяется маркировкой сети Петри [8].

Другим преимуществом ССП является их внутренняя способность обрабатывать любое распределение времени до перехода, например, неэкспоненциальные переходы, в отличие от марковского подхода, который требует более сложных операций для управления частотой отказов, изменяющейся во времени (например, системы, демонстрирующие младенческую смертность или износ) [5]. Хотя первоначально стохастические сети Петри использовались для моделирования и анализа производственных систем и компьютерных сетей, они все чаще стали использоваться для исследований надежности, а также технического обслуживания и анализа рисков из-за многих преимуществ, которые они предоставляют, по сравнению с цепями Маркова [4]. Однако внедрению ССП по-прежнему препятствует ограниченная доступность программного обеспечения для сетей Петри, особенно по сравнению с широкой доступностью программных средств для других подходов к моделированию [1]. Таким образом, в случае сети Петри для захвата общего состояния космического аппарата необходимо 48 позиций, в то время как при марковском подходе – более 16 миллионов состояний. Пространство состояний для цепи Маркова (или полумарковской модели) сделало бы ее неуправляемой и невозможной для визуализации. Кроме того, количество законов перехода для вычисления и заполнения модели было бы неуправляемым.

В работе рассматриваются следующие 11 подсистем космического аппарата, а также неизвестные причины отказов:

• 1.    Гироскоп/солнечный датчик.

• 2.    Двигатель/топливная система двигателя.

• 3.    Функционирование антенны.

• 4.    Центральная вычислительная машина.

• 5.    Механизмы.

• 6.    Полезная нагрузка.

• 7.    Аккумуляторная батарея.

• 8.    Распределение электроэнергии.

• 9.    Развертывание солнечных батарей.

• 10.    Работа солнечной батареи.

• 11.    Телеметрия, слежение и управление.

В базе данных, используемой для проведения статистического анализа отказов для этой работы, когда подсистема-виновник не может быть идентифицирована, аномалия или отказ космического аппарата отнесены к категории неизвестных [3].

Диаграмма состояния отказа для каждой подсистемы показана на Рисунке 3.

Возможность применения к космическим системам стохастических сетей Петри ...

Полностью работоспособный

Класс I

Полный отказ

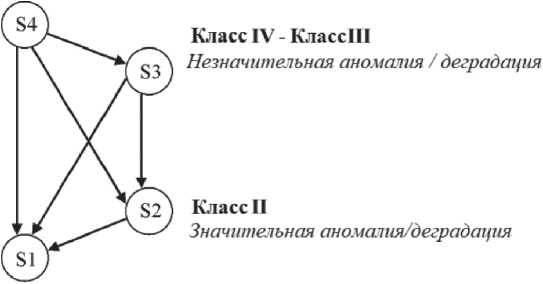
Рисунок 3. Переходная диаграмма отказоустойчивости подсистем космического аппарата

Как только вероятности перехода между каждым состоянием для каждой подсистемы вычислены, статистическое поведение подсистем при отказе в нескольких состояниях будет смоделировано с использованием стохастических сетей Петри.

Система обеспечения живучести и ССП. Живучесть системы связана с ухудшением производительности. Реакция системы после воздействия характеризует способность системы к восстановлению, которую в простых терминах можно рассматривать как время, необходимое системе для восстановления в пределах определенного процента от ее первоначального уровня производительности [2].

На Рисунке 4 представлена условная реакция системы, столкнувшейся с воздействием или сбоем.

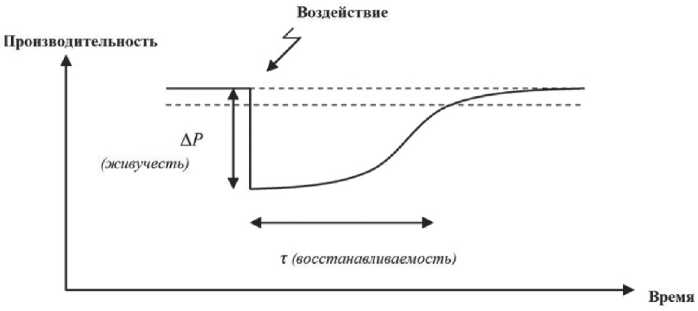
Рисунок 4. Номинальная реакция системы после воздействия

Автором предложена структура (см. Рисунок 5) анализа живучести системы.

Рисунок 5. Структура живучести системы

Живучесть, как и концепция оптимизации, остается нечетко определенной, если не будет предоставлена дополнительная информация, что система оптимизирована по отношению к последнему и что система жизнеспособна по отношению к первому. Характеристика классов угроз или типов сбоев, представляющих интерес, – первый шаг в анализе живучести [7]. Второй шаг ориентирован на проектирование и направлен на характеристику архитектуры рассматриваемой системы, ее (функциональной) структуры и вариантов проектирования (например, модульности, избыточности и др.) функций, которые относятся к ее производительности. Третий шаг преобразование предыдущего в аналитическую или вычислительную модель системы для оценки ее живучести в отношении классов угроз или типов сбоев, представляющих интерес. Эти инструменты включают в себя решетчатые графики, марковские процессы (с моделированием по методу Монте-Карло). Стохастические сети Петри используются для третьего шага по причинам, отмеченным ранее. Последний шаг состоит в оценке снижения производительности системы – оценке ее живучести после сбоев с использованием ранее разработанной модели системы и характеристики классов угроз или типов сбоев, представляющих интерес (см. шаг 1).

Стохастические сети Петри представляют особый интерес для разработчиков моделей, поскольку они позволяют моделировать различные «слои» интересующей системы, то есть модели на разных уровнях интеграции [9]. Действительно, в случае систем с несколькими подсистемами или в случае системы систем каждая подсистема может моделировать свои состояния независимо, создавая «уровень подсистемы». Таким же образом могут быть смоделированы «системные уровни», чтобы связать подсистемы между собой, если они взаимосвязаны (зависимые сбои, каскадные сбои, распределение нагрузки и др.). Для моделирования влияния сбоя подсистемы на состояние всей системы «уровень проектирования» завершает модель с помощью соответствующих переходов, дуг ингибиторов или активаторов.

Применение стохастических сетей Петри при анализе живучести космических систем

Для иллюстрации применения одной из стохастических сетей Петри представлен анализ живучести для двух типов космических архитектур – традиционного монолитного космического корабля и космической сети, которые анализируются в отношении ограниченных аномалий и сбоев на орбите благодаря физическому распределению функций в нескольких орбитальных модулях, подключенных друг к другу по беспроводной сети. Предварительный анализ показывает, что такая архитектура при определенных условиях, несмотря на некоторые первоначальные расходы, предлагает ряд преимуществ по сравнению с традиционной монолитной конструкцией космического аппарата.

Разработка модели ССП. В следующем примере рассмотренная космическая сеть проста и состоит из двух объединенных в сеть космических аппаратов.

Первый космический аппарат S/C № 1 (см. Рисунок 6) содержит все подсистемы, как и монолитный космический аппарат. Однако у него есть возможность поддерживать связь с другим космическим аппаратом S/C № 2.

Второй космический корабль имеет необходимые подсистемы для космического корабля плюс подсистемы функционирования антенны, ЦВМ и телеметрии, слежения и управления, к которым S/C № 1 может подключаться или использовать эти системы в случае повреждения или выхода из строя своих систем. Беспроводная связь в космической сети обеспечивает своего рода резервирование двух космических аппаратов в сети.

Каждая подсистема может быть смоделирована с использованием четырех состояний подсистемы:

• –    состояние системы 4 – полностью работоспособное;

• –    состояние системы 3 – незначительное ухудшение;

• –    состояние системы 2 – значительное ухудшение;

• –    состояние системы 1 – сбой.

Возможность применения к космическим системам стохастических сетей Петри ...

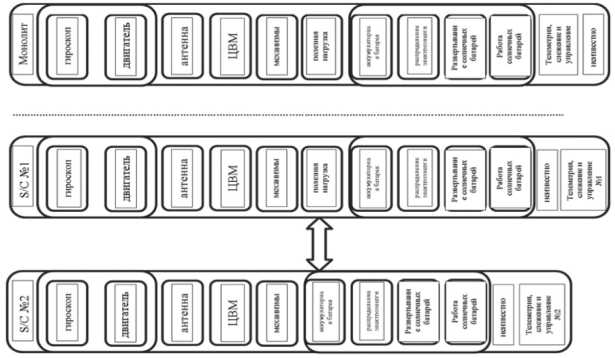
Рисунок 6. Архитектура монолитного космического аппарата (вверху) и космической сети (внизу)

Эти состояния определяют уровень точности для анализа живучести моделей.

На основе этих правил и конкретных вариантов проектирования подсистем в каждом космическом аппарате (как показано в нижней части Рисунка 6) модель ССП, разработанная для этой конкретной космической сети, показана на Рисунке 7. Места и переходы, не охватываемые компонентами, кодируют правила, связывающие состояния подсистемы с состояниями системы, описанными ранее, – «уровень проектирования» сети.

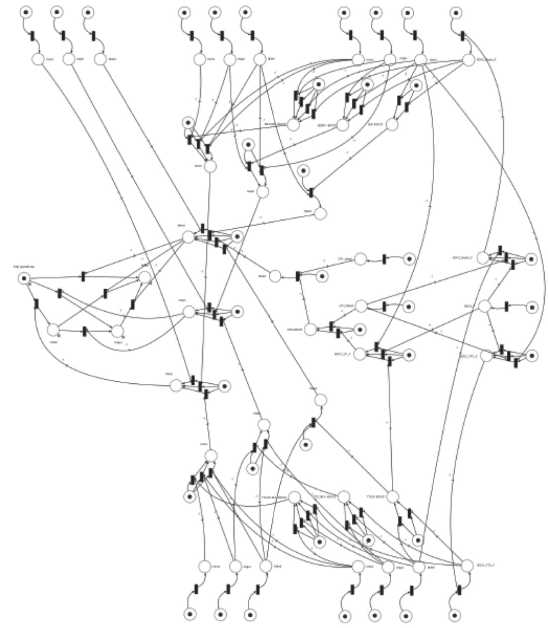
Рисунок 7. Модель ССП космической сети

Из-за стохастической природы ССП моделирование методом Монте-Карло необходимо для получения репрезентативного поведения случайных переходов и других статистических данных, представляющих интерес. Учитывая относительную сложность моделей ССП наших космических систем, было проведено моделирование методом Монте-Карло с 10 миллионами запусков, чтобы должным образом отразить эволюцию во времени вероятностей того, что система находится в рабочем или различных отказавших состояниях (т.е. незначительное, или значительное ухудшение, или сбой).

На Рисунке 8 представлены результаты, показанные на двух разных графиках для удобства чтения с учетом их разных диапазонов по оси Y .

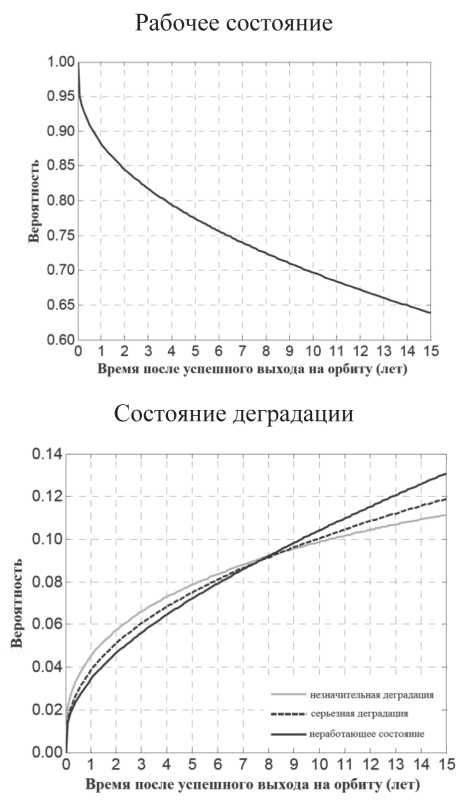
Рисунок 8. Результаты оценки вероятности состояния модели ССП космической сети

Прокомментируем Рисунок 8. Например, после пяти лет на орбите смоделированная космическая сеть имеет 79,3 % вероятности полной работоспособности, 7,4 % – незначительной деградации, 7,5 % – значительной деградации и 5,8 % – состояния сбоя.

Возможность применения к космическим системам стохастических сетей Петри ...

Заключение

Проанализирована применимость ССП к анализу отказов и живучести в нескольких состояниях. После краткого ознакомления с сетями Петри можно утверждать, что ССП лучше подходят для этого типа анализа, чем цепи Маркова. Предложена общая основа для анализа живучести системы и проиллюстрирована ее применимость на примерах космических систем. Произведено сравнение живучести двух космических архитектур – монолитного космического корабля и космической сети, которая допускает распределенное резервирование определенных подсистем. Моделирование методом Монте-Карло проведено для получения репрезентативных результатов стохастического поведения двух архитектур в отношении аномалий и сбоев на орбите.