Возможности алгоритма сверток с производными для оценки параметров масс-спектров, содержащих наложившиеся пики

Рассматриваются результаты исследования возможностей алгоритма сверток исходного сигнала со второй и четвертой производными функций, описывающих форму спектральных линий. Приводятся погрешности оценок амплитуд, положений и ширин спектральных пиков после проведения процедуры разделения наложившихся пиков для сигналов с разными значениями дисперсии шума, разными значениями амплитуд в наложившихся пиках и разными расстояниями по шкале масс отдельных пиков в мультиплетах. Исследование проведено с помощью вычислительного эксперимента с использованием компьютерных моделей масс-спектрометрических сигналов, искаженных шумами для мультиплетов с различными амплитудами отдельных пиков и различными расстояниями между ними.

Кл. сл. : методы обработки сигналов, масс-спектрометрия, оценка параметров пиков в мультиплетах, анализ погрешностей алгоритмов обработки данных

ПОСТАНОВКА ЗАДАЧИ

Большинство масс-спектрометрических пиков можно описать гауссовой функцией. Как известно, пик гауссовой формы описывается формулой

S 2 ( t ) =

t

V цо

^- 1 I exp

f   t2 A

-yr I,

V 2 ц J

S 4 ( t ) =

S ( t ) = A • exp

⁽ t   t max )

2 ц ² J

где А — амплитуда пика; µ — – полуширина пика; t — независимая переменная; t max — положение вершины на оси независимой переменной .

Как отмечалось в работах [1–4], масс-спектр можно рассматривать как сумму суперпозиции пиков гауссовой формы. Предположим, что независимая переменная t меняется непрерывно на вещественной оси (- да , да ). Таким образом, полезная составляющая спектра равна

Y ⁽ t ) = Е A s • ^exP s

⁽ t   t max s )

2 Ц ²

,

где s — номер пика в спектре; A s — амплитуда s -го пика спектра; µ s — полуширина s -го пика; t max s — положение вершины s -го пика спектра.

Рассмотрим подробнее алгоритм оценки параметров масс-спектрометрических пиков, основанный на вычислении сверток с производными четных порядков гауссовых пиков. Выпишем формулы производных гауссианы второго и четвертого порядков:

V Ц

6 t ² 7

+ 3 I exp Ц J

f    t 2 A

-yr I.

V 2ц 2 J

В формулах (3) и (4) через µ ₀ обозначена полуширина пика в функции, описывающей форму пика. Эти функции "подобны" пику в том смысле, что имеют экстремумы при t = 0.

Теперь рассмотрим свертки – S 2 ( t ) и S 4 ( t ) с отдельно взятым пиком:

. да f t ² V ,

У 2 ^{( т} ) = ^- Aj exp I УТ S 2 ^{( T} - t ^)d t ,       ⁽⁵⁾

-да v 2 ц ² j

. да      f    t ² Y,

У 4 ^{( T} ) =^- A l exp l -^ S 4 ^{( T} - t ^)d t .

-да     V 2 ц ² J

В формулах (5) и (6) µ — полуширина пика в исходном сигнале, A — амплитуда пика в исходном сигнале. Взяв интегралы, получим:

У 2 ^{( т} ) = ^А ц ^{п V}2/ [ 1 + ( ^Ц Ц о ) ² У ^x

x[(1- T 7 (ц2+ц2 ))• exp (-T 7 (ц2+ц2))],     (7)

У 4 ( т ) = Ацп¹²/ ^[ 1 + ( цц о ) ² У x x ( 3 - 6 т ²/ ( ц ² + ц² ) ) +

+ Т 4/ ( ц ² + Ц 2 ) 2 ■ exp ( — т 2/ ( ц ² + ц ² ) ) .          (8)

Из формул (7) и (8) следует:

• •    при т = 0 у ₂( т ) и у 4 ( т ) имеют абсолютный максимум;

• •    у 2 (0) / у 4 (0) = [1 + ( ц / Ц о )²] / 3;

• •    если у обеих сверток в одной и той же точке имеются максимумы, то это значит, что на экспериментальной кривой в этом месте расположен пик, а в данной точке — его вершина.

Таким образом, производится обнаружение пика в спектре. Можно доказать, что система функций на основе производных четных порядков { S n ( t )} является ортогональной. В базисе этой системы может быть представлен сигнал исследуемого масс-спектра. Выполнение операций свертки при n = 2 и n = 4 дает возможность выделить пик в заданной точке оси масс, если он там существует. В дальнейшем по значению сверток в максимуме, используя формулы (7) и (8), можно вычислить полуширину µ и амплитуду А обнаруженного пика.

Обозначим значение свертки y 2 ( τ ) в максимуме как С 2 , а значение свертки y 4 ( τ ) в максимуме как С 4 , тогда

Ц = Цо ■

f ³

V С 4

—

A =

C 2

1+ц15

V ц

2 πµ

.

Для дискретных отсчетов (7) и (8) имеют вид:

+ N

Y2( tk ) =Z ^2( ti) У (tk — tJ, i =— N

+ N

Y 4 ( t k ) = Z ^ 4 ( t ) У ( t k - t^.

i =— N

Здесь оказалось возможным перейти от интегрирования по бесконечному интервалу к конечным суммам, т. к. гауссова функция и ее производные быстро убывающие — уже на расстоянии в несколько µ 0 уменьшаются до машинного нуля (т. е. становятся по модулю меньше минимального положительного вещественного компьютерного числа).

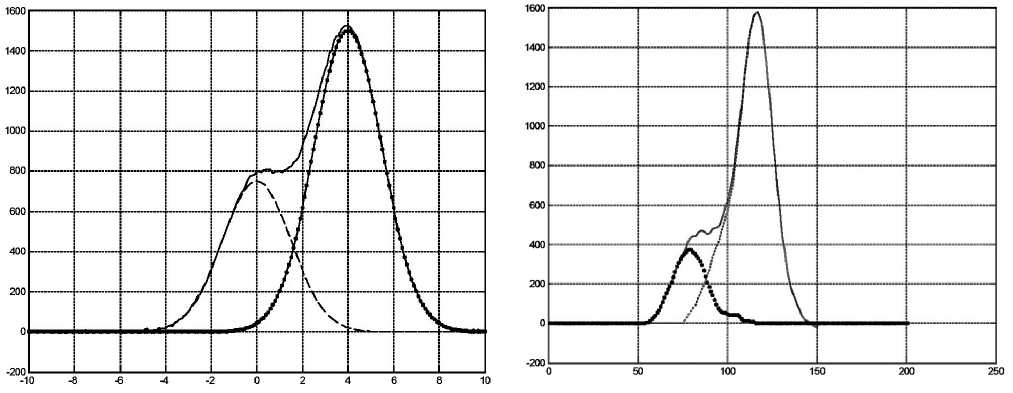
Рис. 1. Сигнал с наложившимися гауссовыми пиками со степенью наложения 0.375 без добавления шума, отношение амплитуд 2 : 1.

Сплошная линия — суммарный пик, штриховая линия и линия с точками — отдельные пики в дуплете

Рис. 2. Сигнал с наложившимися пиками, полученными из экспериментальных данных, со степенью наложения 0.395 без добавления шума, отношение амплитуд 4 : 1.

Сплошная линия — суммарный пик, штриховая линия и линия с точками — отдельные пики в дуплете

МОДЕЛИРОВАНИЕ СИГНАЛА, СОДЕРЖАЩЕГО НАЛОЖИВШИЕСЯ ПИКИ, ДЛЯ ИССЛЕДОВАНИЯ И ОЦЕНКИ

ПАРАМЕТРОВ АЛГОРИТМА СВЕРТОК С ПРОИЗВОДНЫМИ

Для исследования возможностей указанного выше метода оценки параметров сигналов, содержащих наложившиеся пики, использовались модели двух типов:

• 1)    масс-спектр представляет собой совокупность пиков, форму которых можно описать гауссовыми функциями с различными амплитудами и ширинами;

• 2)    описание формы пиков масс-спектра основано на реальных экспериментальных данных, полученных на масс-спектрометре с квадрупольным анализатором.

Модели каждого из двух типов имеют наложившиеся пики и аддитивный шум. Степень наложения определяется параметром N = µ / L, где µ — полуширина пика в соответствии с формулой (1), L — расстояние между центрами наложившихся пиков. Шум, добавляемый к моделям пиков двух типов, генерировался с помощью датчика случайных чисел, имеющих плотность рас- пределения, соответствующую нормальному закону с задаваемой программно дисперсией и нулевым математическим ожиданием.

На рис. 1 представлена модель двух наложившихся пиков гауссовой формы со степенью наложения N = 0.375. Для данной модели L = 4, µ = 1.5. Соотношение амплитуд 2 : 1 (амплитуда большого пика 1500, малого пика 750).

На рис. 2 представлена модель двух наложившихся пиков, форма которых соответствует экспериментальным данным, полученным на масс-спектрометре с квадрупольным анализатором. Наложившиеся пики получены путем сближения одиночных пиков реального масс-спектра.

На рис. 3 и 4 представлены те же модели сигналов соответственно, что и на рис. 1, 2, но наложившиеся пики сдвинуты относительно друг друга до степени наложения N = 1.

На рис. 5 и 6 представлены те же модели сигналов, что и на рис. 3, 4, но с добавлением шума. Отношение сигнал/шум ( R ) определяется как отношение амплитуды минимального пика к среднему квадратичному отклонению дисперсии шума. Для представленных моделей отношение сиг-нал/шум R = 10.

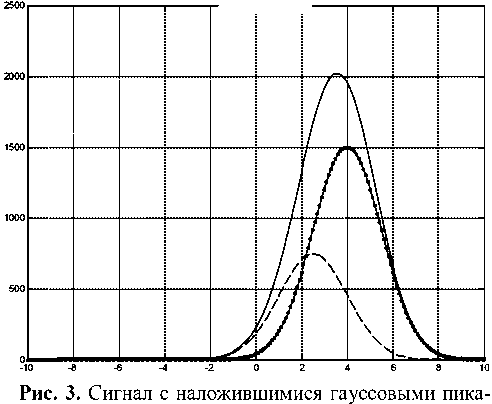
ми со степенью наложения 1 без добавления шума, отношение амплитуд 2 : 1.

Сплошная линия — суммарный пик, штриховая линия и линия с точками — отдельные пики в дуплете

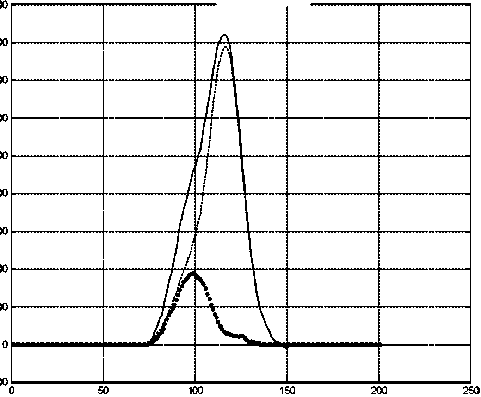
Рис. 4. Сигнал с наложившимися пиками, полученными из экспериментальных данных, со степенью наложения 1 без добавления шума, отношение амплитуд 4 : 1.

Сплошная линия — суммарный пик, штриховая линия и линия с точками — отдельные пики в дуплете

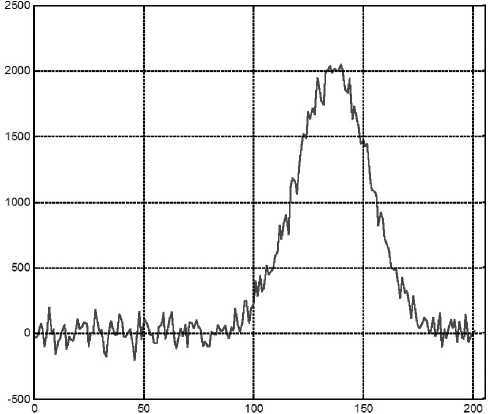
Рис. 5. Сигнал с наложившимися гауссовыми пиками со степенью наложения 1 с добавлением шума, отношение амплитуд 2 : 1.

Отношение сигнал/шум R = 10

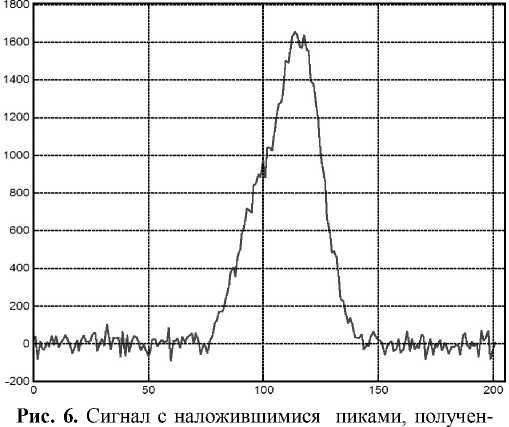
ными из экспериментальных данных со степенью наложения 1 с добавлением шума, отношение амплитуд 4 : 1.

Отношение сигнал/шум R = 10

Табл. 1. СКО оценок параметров отдельных сигналов в дублетах ( N = 0.85) с соотношением амплитуд 5 : 1 при различных отношениях сигнала к шуму

Сигнал/ шум	СКО оценки, %
	Амплитуда		Ширина
	гаусс	квадр	гаусс	квадр
10	3	3	0.1	0.1
50	0.5	0.8	0.05	0.05
100	0.1	0.3	0.05	0.05

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ НА МОДЕЛЯХ СИГНАЛОВ АЛГОРИТМА СВЕРТОК С ПРОИЗВОДНЫМИ ДЛЯ ОЦЕНКИ

ПАРАМЕТРОВ МАСС-СПЕКТРОВ, СОДЕРЖАЩИХ НАЛОЖИВШИЕСЯ ПИКИ

Для определения возможностей указанного алгоритма с помощью вычислительного эксперимента определялись средние квадратичные отклонения (СКО) оценок отдельных параметров сигналов в дублетах при различных реализациях налагаемого шума. СКО оценок параметров отдельных сигналов в дублетах с соотношением амплитуд (5 : 1) по результатам проверки алгоритма "свертка с производными …" при различных отношениях сигнала к шуму и степени наложения N = 0.85 для пиков гауссовой формы (гаусс) и эксперимен- тальных данных квадрупольного масс-спектрометра (квадр) представлены в табл. 1.

СКО оценок параметров дублетов для отдельных сигналов с соотношением амплитуд 5 : 1 по результатам проверки алгоритма "свертка с производными …" при различной степени наложения N и отношении сигнал/шум 50 для пиков гауссовой формы (гаусс) и экспериментальных данных квадрупольного масс-спектрометра (квадр) представлены в табл. 2.

Погрешность положения центра пика для всех случаев не превышала шага дискретизации по оси масс.

СКО оценок параметров дублетов для отдельных сигналов с различным соотношением амплитуд по результатам проверки алгоритма "свертка с производными…" при степени наложения N = 0.85

Табл. 2. СКО оценок параметров отдельных сигналов в дублетах с соотношением амплитуд 5 : 1 при различной степени наложения ( R = 50)

Степень наложения N	СКО оценки, %
	Амплитуда	Ширина
	гаусс	квадр	гаусс	квадр
0.75	0.5	0.6	0.05	0.05
0.85	0.5	0.8	0.05	0.05
1.00	1.0	1.0	0.1	0.1

Табл. 3. СКО оценок параметров отдельных сигналов в дублетах ( N = 0.85) с различным соотношением амплитуд при R = 50

Отношение амплитуд СКО оценки, % Амплитуда Ширина гаусс квадр гаусс квадр 5 : 1 0.5 1.5 0.05 0.05 10 : 1 0.5 1.7 0.05 0.05 20 : 1 1.6 1.9 0.1 0.1 и отношении сигнал/шум R = 60 для пиков гауссовой формы (гаусс) и экспериментальных данных квадрупольного масс-спектрометра (квадр) представлены в табл. 3. При получении данных в табл. 3 по программе, реализующей рассматриваемый алгоритм, после обнаружения в мультиплете пика с максимальной амплитудой из исходных данных вычитался пик с амплитудой, вычисленной по формуле (10), и формой, соответствующей экспериментальным данным одиночного пика квадрупольного масс-спектрометра (квадр). При увеличении отношения амплитуд до 40 : 1 положения центров пиков оставались практически неизменными, а CКО оценки амплитуды малого пика составляло от 2.5 до 16 % в зависимости от реализации шумового сигнала.

ЗАКЛЮЧЕНИЕ

Рассмотренные возможности алгоритма на основе сверток с производными для оценки параметров масс-спектров, содержащих наложившиеся пики, дают информацию о пригодности такого алгоритма для использования в практической работе при обработке данных со степенью наложения пиков в мультиплетах, не превышающей единицы, и с соотношением амплитуд, не превышающим двадцати. Достоинством алгоритма является низкая погрешность определения положения центров пиков при различных отношениях амплитуд одиночных пиков в мультиплетах.