Возможности и перспективы применения метода СИМ при решении внутренних задач ста

В прямых внешних задачах СТА [1-3] эффективность применения метода СИМ [4-5] показана в [6-12 и др.]. Представляет интерес рассмотрение возможностей метода СИМ для решения внутренних задач СТА – в первую очередь связанных с моделированием законов распределения случайных факторов, влияющих на работу СА в разных режимах ее работы: данные факторы принято называть амплитудными, фазовыми, частотными, временными и геометрическими (пространственными) ошибками. Очевидно, что метод СИМ при этом должен быть развит и адаптирован для решения не только внешних, но и внутренних задач СТА.

Цель статьи – краткий обзор принципов и возможностей метода СИМ, существенных для его использования в интересах СТА, а также обоснование правомерности применения вероятностных моделей, построенных на основе семейства устойчивых распределений, для описания ошибок при решении внутренних задач СТА.

Публикация статьи приурочена к 90-летнему юбилею основоположника современной СТА Я.С. Шифрина.

Принципы СИМ: этапы проведения, задачи и цели

Датой рождения метода СИМ считается 1949 г., когда Н. Метрополис и С. Улам опубликовали в США статью «Метод Монте Карло», в которой впервые изложили его сущность [4]. Для исследования разброса характеристик антенны метод Монте-Карло был применен С. Грином и Р. Моллером в 1962 г. [5]. Однако, по современным представлениям, идеология СИМ гораздо шире идеи использовать в задачах СТА тестовые последовательности так называемых случайных чисел (СЧ), на которой базируется метод Монте-Карло. Хотя одним из решающих факторов здесь стало развитие компьютерных технологий, позволившее удобно и просто для пользователей реализовать важнейшую для метода Монте-Карло процедуру разыгрывания псевдослучайных чисел, – которые при проведении СИМ используются как СЧ [6; 9-12].

Метод Монте-Карло часто называют методом статистических испытаний, а так как в настоящее время эти испытания проводятся с применением ЭВМ, – еще и методом статистического моделирования (который следует отличать от метода СИМ).

Рассматривая перспективы использования в интересах СИМ СА ряда результатов и достижений ТВ последних лет, укажем, во-первых, на предложение использовать при проведении СИМ объектов с малой прецедентной базой модели, построенные на основе предельных распределений ТВ [13]. Во-вторых, на необходимость разработки процедуры компьютерного разыгрывания по методу Монте-Карло последовательностей независимых СЧ, подчиненных одному из таких предельных распределений – устойчивому закону (теоретические аспекты более подробно см. в [14-17]). В этой связи методика СИМ СА может содержать следующие этапы [6].

Этап 1 , предусматривающий определение состава исходных данных (детерминированных и случайных, входных, внутренних и внешних), которые оказывают влияние на процесс функционирования СА; а также выходных характеристик (результатов СИМ) и критериев для оценки путем анализа этих характеристик (результатов) эффективности функционирования СА.

Этап 2, реализующий комплексное(в том числе статистическое) исследование СА путем сбора и обработки информации о ней с целью выявления законов распределения исходных данных, – при этом реальные данные могут быть использованы как для определения непосредственно используемых теоретических законов, так и для получения эмпирических распределений, из которых в дальнейшем можно выбирать исходные данные, необходимые для моделирования СА.

Этап 3, включающий идентификацию типов законовраспределения исходныхданныхи расчет статистических оценок параметров этих законов – в том числе с применением пакетов программ из области прикладной статистики, которые хорошо разработаны и обеспечивают возможность диалогового режима работы пользователя.

Этап 4, который заключается в разработке математических моделей – сначала для каждого блока СА, при необходимости представляемой в виде сложной иерархической системы, а затем для СА в целом, – с последующим программированием СИМ-модели (статической, динамической) на ЭВМ и разработкой плана компьютерного эксперимента для имитации процесса функционирования СА.

Этап 5, состоящий в имитации процесса функционирования СА на разработанной СИМ-модели в виде пакета прикладных программ (обычно в диалоговом режиме) – при необходимости с выводом после каждого цикла моделирования промежуточных данных, на основе которых формируются результаты СИМ.

Этап 6 – завершение эксперимента при достижении заданной доверительной вероятности (надежности) или заданного числа реализаций СИМ-модели, с выводом полученных результатов (массивов выходных расчетных данных), которые подлежат статистической обработке для удобства последующей интерпретации.

Опыт показывает, что конечный успех во многом зависит от того, насколько эффективно создателями СИМ-модели выполнены работы по первым трем этапам, – ориентированным на решение внутренних задач СТА с применением методов и средств ТВ и математической статистики. В этой связи необходимо уточнить ряд положений теории СИМ, важных для их практического применения [18-20].

Структурная схема СА как объекта СИМ с указанием принятых обозначений показана на рис. 1. В качестве исходных данных здесь фигурируют: воздействия A_n ; n [1; N ] , поступающие на вход СИМ-модели, а также иные воздействия B_m ; m [1; M ], поступающие извне; результаты СИМ, получаемые на выходе модели Y_z ; z [1; Z ] ; и две группы характеристик модели – не представляющие интерес (с точки зрения их влияния на результаты СИМ) в рамках проводимого эксперимента C_k ; k [1; K ], и W_r ; r [1; R ], влияние которых на Y_z исследуется методом СИМ.

Внешние воздействия Вь..Вм

Выходные результаты

«Блок W»

Рис. 1. К постановке задачи СИМ

Будем считать, что целью эксперимента с применением СИМ является оптимизация «Блока W» (в качестве которого могут выступать сигналы, физические схемы и цепи, алгоритмы и варианты программного обеспечения – ПО, количественные характеристики аппаратуры, режимы работы и т.д.) в составе модели СА путем определения параметров W_r ; r [1; R ], обеспечивающих наилучшие показатели результатов СИМ Y_z ; z [1; Z ] , в соответствии с предварительно выбранным критерием эффективности. При этом также считается, что если известны все значения A_n ; B_m ; C_k ; W_r ; n ; m ; k ; r и т.д.; то результаты СИМ могут быть найдены на основании аналитической зависимости вида

С точки зрения современной ТВ, в терминах [13], правая часть (1) представляет собой обобщенную сумму случайных аргументов и определяется через совокупность полугрупповых операций, ассоциативных и коммутативных, которые могут иметь стохастический характер, поскольку значения N ; M ; K и R также могут быть СЧ (обобщенная сумма постоянных аргументов, например, также является случайной величиной).

Поиск и исследование законов, которые являются предельными для последовательностей обобщенных сумм (1), является одним из актуальных направлений развития ТВ. Однако форма представления математических результатов – в виде доказательств многочисленных ПТ заметно сужает возможности их применение в интересах прикладных наук. Наблюдается неоднозначная ситуация: с одной стороны, в ТВ постоянно расширяется круг операций, для которых предельные распределения YZ существуют, и снимаются ограничения на случайные обобщенные слагаемые в правой части (1), – такие как одинаковый характер распределения, независимость и равномерная предельная пренебрегаемость, линейный характер суммирования и т.п. Показано, что путем нелинейного нормирования обобщенных слагаемых можно получить предельные законы для неодинаково распределенных и взаимно зависимых, «сильно рассеянных» аргументов, формирующих YZ путем случайного сложения, умножения, возведения в степень, выбора по максимуму и других аналогичных операций. Эта тенденция полностью отвечает запросам инженера, занятого решением прикладных задач, поскольку позволяет ему в своих разработках все чаще опираться на мощный фундамент в виде совокупности ПТ.

С другой стороны, согласно [13], существуют три уровня практической значимости ПТ ТВ. Первый из них, в нашей терминологии, соответствует определению факта существования предельного распределения Р ( Y_Z ) для рассматриваемой последовательности значений Y_Z . Второй уровень устанавливает существование критерия 5 ( Y_Z ), который служит оценкой приближения реальных распределений последовательности Y_Z к предельному закону Р ( Y_Z ). Наконец, третий уровень определяет числовые значения б ( Y_Z ), передающие динамику приближения реальных распределений к Р ( Y_Z ). При этом отмечается, что из многих сотен, если не тысяч ПТ ТВ, лишь немногие можно отнести к третьему, наиболее важному для практики уровню, – тогда как огромная масса остальных пребывает на качественном первом уровне.

Любая из ПТ ТВ может быть полезной, если «подскажет» вид аппроксимирующего предельного распределения и создаст основу для СИМ – особенно когда другим путем это сделать трудно. По выражению автора [22], компьютер в руках специалиста по ТВ при этом становится «микроскопом», с помощью которого он может получать необходимые результаты третьего уровня практической значимости. Да и инженер обычно не ставит перед собой задачу полноценного научного исследования моделируемого объекта – ему важно с помощью СИМ найти ответ на ряд конкретных вопросов прагматического характера. Как было отмечено при рассмотрении рис. 1, для этого достаточно бывает сравнить между собой варианты реализации «Блока W» и определить совокупность параметров WR , обеспечивающих наилучший результат YZ в соответствии с заданным показателем эффективности СА. По аналогии с теорией измерений можно утверждать, что в данном случае представляют интерес не абсолютные знания о данном объекте, погрешность определения которых может быть недопустимо большой, а относительные – приемлемая погрешность которых обеспечит правильность принимаемых с помощью метода СИМ конкретных решений.

Особенности применения метода СИМ для решения внутренних задач СТА

Возможны два подхода к рассматриваемой проблеме, правомерность которых зависит от степени сложности моделируемого объекта. В СА с более простой структурой значения A_n ; B_m ; C_k ; n ; m ; k и др. в (1) можно задать в первом приближении или произвольным образом, а затем варьировать их в необходимых пределах, подвергая статистической обработке массивы выходных значений Y_Z . Затраты машинного времени на решение исследовательских задач при этом не играют особой роли – однако при управлении объектом в режиме on-line такое проведение СИМ может оказаться неприемлемым. К тому же на такой «игрушечной» модели СА легко получить практически любой желаемый результат – в частности, показать, что W_R никак не влияет на Y_Z , что представляется наиболее распространенной ошибкой.

Авторы второго подхода [20-21 и др.] полагают, что избежать таких ошибок можно путем сбора и обработки информации обо всех обобщенных слагаемых – аргументах функции F (AN; BM; CK; XR) в правой части (1). В особой мере это относится к задачам по управлению объектами, имеющими сложную иерархическую структуру – для которых метод СИМ является единственным эффективным способом их решения. Однако при необходимости моделировать объекты с малой прецедентной базой (к числу которых относится большинство СА) здесь также возникают трудности, которые в [18-19] предлагается преодолевать, применяя метод Монте-Карло и ПТ ТВ, приводящие в качестве предельных распределений для последовательностей случайных аргументов и функции F (AN; BM; CK; XR) к се- мейству одномерных устойчивых законов [13-17]. При этом для моделирования случайных воздействий BM на рис. 1 необходимо использовать компьютерные блоки (программы), обеспечивающие генерацию последовательностей СЧ (разыгрывание СЧ), распределенных по устойчивому закону [6; 11-12].

Наиболее эффективным и универсальным способом разыгрывания СЧ, подчиняющихся закону с интегральной функцией распределения (ИФР) P ( x ), считается метод нелинейного преобразования, обратного заданному закону:

где Р ^–1 – обратная функция для ИФР P ( x ) разыгрываемой случайной величины x [ x_m1 ; x_m2 ]; V_s – s -ая реализация случайной величины V , равномерно распределенной на интервале [0; 1]; x_s – s -ая реализация x [21]. Соотношение (2) можно рассматривать как уравнение функциональной связи между случайными значениями x_s и V_s . Стандартное ПО современных ЭВМ включает «датчики» взаимно независимых СЧ V_s , поэтому получение последовательности S значений x_s на компьютере не представляет труда, если известна обратная функция Р ^–1 .

Процедура исследования СА в интересах определение типа и параметров функции Р ^–1 для воздействий B_M представляется одним из слабых мест метода СИМ, поскольку здесь приходится искать компромисс между целым рядом противоречивых требований:

• -    приемлемая простота способа получения объема статистических данных, необходимого и достаточного для обеспечения репрезентативности выборок и достоверности полученных оценок;

• -    непродолжительность времени получения указанных данных при исследовании динамических (нестационарных) объектов;

• -    корректность (несмещенность, эффективность, состоятельность) статистических оценок, найденных в данный момент времени;

• -    пригодность выбранной модели P ( x ) для прогнозирования будущего состояния объекта с учетом его динамики;

• -    реализация выбранной модели на ЭВМ с возможностью ее оперативной коррекции и т.д.

Также сложно решаются вопросы обоснованного выбора типа P(x) – поскольку используемые статистические критерии (Пирсона и др.) не дают однозначного ответа и лишь «не отвергают» гипотезы соответствия найденной ИФР нескольким типовым распределениям (чаще всего это финит- ные варианты экспоненциального и нормального законов, а также равномерный закон).

Статистическое исследование предметной области СИМ (в нашем случае – с целью определения законов распределения ошибок разных видов в СА) считается обязательным этапом моделирования как в теории СИМ, так и в СТА. Хотя применительно к виртуальным объектам (к числу которых относятся проектируемые, прогнозируемые, разведанные и т.п. СА) говорить о проведении таких исследований не приходится. Выходом из ситуации является применение для моделирования ошибок в СА метода СИМ, адаптированного к решению внутренних задач СТА.

Моделирование ошибок в СТА

Поиск универсальной СИМ-модели, из которой, как минимум, можно получать все варианты распределений ошибок, близкие реальным законам, приводит к семейству устойчивых распределений [6; 13-17]. Напомним, что существование этих законов в качестве предельных для последовательностей Y_Z в (1) обусловлено постоянно расширяющимся кругом ПТ ТВ, что в определенной мере также гарантирует эффективность их применения. Наиболее распространенная форма записи характеристической функции (ХФ) одномерного устойчивого закона имеет вид

№ = ex^aU-b |[/|^[1 +J4W\U\MU-, /)]}, (3)

где             – аргумент ХФ;

γ (0; 2] – параметры устойчивого закона, причем

w(U;y^

- tg (я у / 2 ); (2 /я) hi \u\ у * 1, / = 1.

Соответствующая (3) центрированная (α = 0) и симметричная (с = 0) плотность распределения вероятности (ПРВ) случайной величины X = YZ (соответствующей ошибке заданного вида) есть wi(JQ = (l/л") J exp( -bUY) cos(UX) dU, (4) о где U [ 0; Um]; Um – граница существенной области преобразования Фурье S1(±Uт) [16] для аргумента ХФ. Нормальному закону с параметрами α и 2b при соответствует γ = 2.

Значение Um в (4) зависит от размеров области распределения каждого обобщенного слагаемого в (1) и от размеров областей изменения соответствующих им аргументов ХФ – границы которых определяют точность обратного преобразования Фурье. Функция ПРВ должна отвечать условию нормировки

Jw,(^) dX = 1 - e„ ,        (5)

где e.^ ¹ – заданная величина, регулирующая точность расчета. Для определения U_m в рамках метода СИМ эффективным является метод, использующий правило Парсеваля, по аналогии с теорией спектров [16]. Границы области S ₁ (± U_т ) при этом определяются сравнением результатов интегрирования ХФ Z(^)) на комплексно-сопряженную функцию /1 (U ) в бесконечных U [–∞,∞] и конечных U [– U_т , U_т ] пределах:

VWitDdu

Рф.) = ^------;------- = 1 " ^   (6)

V^uVfAuw

где ε << 1 – параметр, регулирующий точность расчета. После определения границ S ₁ (± U_т ) для вычисления ПРВ (4) могут быть использованы стандартные процедуры ПО Mathematica [23], адаптированные в интересах СИМ.

Отметим ряд важных обстоятельств. Во-первых, если доказана предельная сходимость последовательности значений X_n к устойчивому закону для усеченной области [ X₁ ; X₂ ], то при изменении ее границ тип ХФ (3) не изменяется. Во-вторых, при учете взаимных связей аргументов (как детерминированных, так и случайных) в рамках схемы обобщенного суммирования (2), вид ХФ (3) также не изменяется. В-третьих, случайные аргументы в (1) по своей физической сущности удовлетворяют условиям ПТ ТВ [13-15], поэтому центрировать и нормировать их при определении для них в качестве предельных законов (3)-(4) не-обходимостинет–темболее, чторечь витогеидет об асимптотических, то есть всегда приближенно выполняемых соотношениях [16-18]. В-четвертых, условие о существовании единственного предельного распределения для последовательности X здесь также всегда выполняется по физическим причинам. В-пятых, финитныеПРВ с γ > 2, по терминологии [16], именуются формально устойчивыми моделями: они напрямую не связаны с ПТ ТВ, однако могут возникать, например, в результате нелинейных преобразований случайных величин в антеннофидерном тракте. При γ < 2 коэффициент эксцесса ПРВ (4) является положительным, для формально устойчивых ПРВ (при

γ > 2) он отрицателен. В-шестых, при прохождении сигналов через любые нелинейные элементы или после обработки их по любым известным алгоритмам, модель (3)-(4) остается в силе, если это укладывается в схему (1). Для выполнения условия нормировки в области X [ X₁ ; X₂ ] устойчивый закон должен быть усечен [16; 24-25].

Изложенное показывает, что устойчивая модель (3)-(4) обобщает нормальный закон, имея с ним единый теоретический фундамент в виде ПТ ТВ, но обладает существенно большими возможностями для воспроизведения свойств F ( A_N ; B_M ; C_K ; W_R ) в правой части (1). При этом в частных случаях она близка к наиболее часто используемым при проведении СИМ финитным вариантам экспоненциального и нормального законов, а также к равномерному распределению [24] – что вполне соответствует требованиям к универсальной модели ошибок.

Известные способы разыгрывания СЧ [21; 26 и др.] трудно использовать для формирования последовательностей СЧ, подчиняющихся устойчивому закону, ввиду проблем, связанных с нахождением обратной функции Р ^–1 (■) для (3)(4). Выходом является использование вместо (2) уравнения P ( x_s ) = V_s и решение его по модифицированной процедуре [6; 1 1; 25]. Достоинствами такого способа являются сокращение продолжительности процедуры разыгрывания по сравнению с аналогами, а также упрощение поиска значений СЧ при приемлемом увеличении ресурсов памяти ЭВМ. Это обусловлено тем, что используемые массивы СЧ можно определить один раз, – чтобы впоследствии для чистоты серии проводимых в рамках СИМ экспериментов использовать одну и ту же последовательность входных или промежуточных данных.

Напомним, что разыгрывание непрерывной случайной величины R означает получение последовательности ее возможных значений R_k , где k G [1; N_R ], соответствующих известной ИФР P ( R ) [21]. Если r _k – значение случайного числа r , равномерно распределенного на интервале (0; 1), то возможное значение R_k разыгрываемой непрерывной случайной величины R с заданной ИФР P ( R ), соответствующее r _k , является корнем уравнения P ( R _k ) = r _k . Однако для одномерного устойчивого закона ИФР, соответствующая (4), в данных обозначениях представляет собой

ЛЛ) = (l/2n) dR f¹' "² МЩ Qy^-jUR W , (7)

где [Um1 ; Um2 ]; [Rm1 ; Rm2 ] – границы существенной области преобразования Фурье, поэтому значение R k не может быть найдено аналитическим путем. Уравнение P(R k) = r k удается решить численно при помощи итерационной процедуры, включающей три этапа.

На первом этапе, после определения границ существенной области преобразования Фурье со- гласно [16]:

• 1)    интервал значений P ( R ) (0; 1) делится на N₀ = 10³ … 10⁵ значений r _k с постоянным шагом

= 10 –3 … 10 –5 («сетка» по оси ординат на графике ИФР);

• 2)    решение уравнения P ( R ) = r _k осуществляется во всех N ₀ указанных точках r _k (то есть с шагом ), в результате чего формируется

последовательный ряд упорядоченных неслучайных значений R_k («сетка» по оси абсцисс на графике ИФР), где k [1; N_R ] и границами k -го интервала шириной являются

R

k1 ^{; R} k2 ^.

На втором этапе:

• 3)    с помощью компьютерного генератора СЧ разыгрывается значение r_k на интервале (0; 1) оси

ординат;

• 4)    определяются границы соответствующего ему k -го интервала R_k1 ; R_k2 на оси абсцисс;

• 5)    рассчитывается первая граница интервала поиска R_m1 = ( R_k1 + R_k2 )/2;

• 6)    в точке R_m1 рассчитывается значение ИФР и находится разность rk – P ( R_m1 );

• 7)    в зависимости от знака разности устанавливается вторая граница интервала поиска: R_m2 = R_k1 при r_k – P ( R_m1 ) < 0 или R_m2 = R_k2 при r_k – P ( R_m1 ) > 0;

• 8)    модуль разности сравнивается с абсолютной погрешностью расчета ИФР ε и при | r_k – P ( R_m1 ) | >  ε определяются новые границы R_m1 и R_m2 интервала поиска с уменьшенной вдвое шириной (путем деления его пополам аналогично п.5), в пределах которого находит-

• ся значение rk ;

• 9)    действия по п.п.6-8 повторяются до тех пор, пока не будет достигнута заданная точность расчета: то есть до выполнения для последнего значения R_m ≈ R_k условия | r_k – P ( R_m1 ) | <  ε ;

• 10)    действия по п.п.3-9 повторяются N_R раз, в результате чего формируется последовательный ряд упорядоченных по номерам k СЧ R_k , определенных с заданной точностью ε .

На третьем этапе:

• 11)    с помощью компьютерного генератора СЧ разыгрывается N_ρ целых равномерно распределенных чисел k из массива [1; N_R ];

• 12)    осуществляется выбор СЧ R_k из массива k [1; NR ] по их случайным номерам k , (посколь-кукаждомуномерусоответствуетнайденноечисло

R_k ), в результате чего получается неупорядоченная последовательность из N_ρ случайных значений R_k , подчиненных закону с ИФР P ( R ) заданного вида (в рассматриваемом случае – одномерному устойчивому закону), используемая в дальнейшем для проведения СИМ.

Достоинствами данного способа разыгрывания СЧ являются сокращение продолжительности его процедуры по сравнениюсаналогами [21;26],пос-кольку все перечисленные действия производятся на интервале << 1, а также упрощение поиска значения R_k (корректировка границ интервала поиска R_m1 и R_m2 производится в фиксированных пределах одного шага «сетки» по оси абсцисс), при приемлемом увеличении ресурсов памяти ЭВМ. Указанным путем формируется массив значений R _k , с заданной точностью соответствующий произвольному закону с ИФР P ( R ).

Результаты тестирования алгоритмов и моделирования ошибок

В [6; 13-17] рассмотрены четыре модели, соответствующие частным случаям,когда ПРВ одномерного устойчивого закона (4) может быть вычислена в аналитическом виде: через элементарные функции (на основе нормального закона при = 2 и закона Коши при = 1), а также через специальные функции (косинус-интеграл и синус-интеграл Френеля при = 1/2 и функцию Уиттекера при = 2/3). Для реализации данных моделей можно использовать как ПО Mathematica, так и непосредственно языки высокого уровня (С++, Delphi, Visual Basic и др.). Возможности ПО Mathematica [23] позволяют в удобном для пользователя диалоговом режиме определять ПРВ для ХФ вида (3) с точностью 1-2%, чего вполне достаточно для тестирования алгоритмов моделирования ошибок (подробнее см. в [25]).

Р(Х^

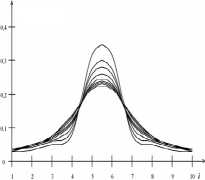
Рис. 2. Сглаженные гистограммы /УХ) для у [0.2; 1]

?№)

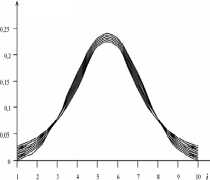
Рис. 3. Сглаженные гистограммы Р^Х^ для у [1; 2,3]

Результаты СИМ иллюстрируют сглаженные гистограммы P(Хi) попадания моделируемой случайной величины X [1; 10] в интервалы Xi с номерами i [1; 9], представленные в качестве примера на рис. 2-3. Графики на рис. 2 соответствуют об- ласти γ [0,2; 1], графики на рис. 3 – области γ [1; 2,3], где кривые идут с шагом по γ, равным 0,1. При этом на рис. 2 верхняя кривая в максимуме соответствует γ = 0,2; а нижняя – γ = 1; на рис. 3, напротив – нижняя кривая в максимуме соответствует γ = 1; а верхняя – γ = 2,3.

Анализ результатов СИМ, аналогичных представленным на рис. 2-3, показывает, что предложенные алгоритмы разыгрывания и тестирования СЧ, распределенных по одномерному устойчивому закону, позволяют воспроизводить широкий круг ПРВ (при γ = var ) с заданной (регулируемой) точностью [6; 1 1; 25]. Поэтому можно утверждать, что данные алгоритмы обеспечивают реализацию универсальной модели ПРВ ошибок w₁ ( X ) в интересах применения метода СИМ с использованием принципа Монте-Карло для решения внутренних задач СТА.

Методику СИМ, ориентированную на формирование N взаимнонезависимых массивов СЧ, соответствующих СА с N независимыми элементами, удается обобщить на случай линейной зависимости между СЧ – например, для учета взаимной пространственной корреляции ошибок, как это принято в СТА [1-3]. При этом значения коэффициентов корреляции R_nm между ошибками в n -ом и m -ом элементах объекта можно задать в обобщенном виде

R_nm = exp(-|Ar„„|^ /D⁸_rs), (12) где g = 1…2 – параметр неопределенности моделирования; понимая под Δ r_nm «расстояние» между точками, соответствующими векторам ошибок в n -ом и m -ом элементах объекта в S -мерном виртуальном пространстве; а под D_RS – радиусы S -мерной пространственной корреляции для s -ой составляющей ошибки. Определение закона распределения для Δ r_nm с помощью метода СИМ в разных статистических ситуациях и режимах работы СА является актуальной задачей. В частном случае, по аналогии с [1], можно ограничиться исследованием корреляционных связей между ошибками, обусловленных только пространственным взаимодействием n -го и m -го элементов СА, понимая под D_RS в (12) радиус пространственной корреляции ошибок каждого типа.

Дляпреобразования N массивовсгенерирован-ных независимых СЧ объемом NV в N массивов устойчивых случайных величин, моделирующих ошибки Х [–Хm; Хm] с заданными корреляционными свойствами, можно воспользоваться методом линейного преобразования [26]. Идея метода заключается в матричном преобразовании вида Y=AX, гдеХ— вектор-столбец «входных» некор- релированных значений Х; Y – вектор-столбец «выходных» коррелированных значений Y ; А – квадратная матрица преобразования размером N^N, элементы которой а вычисляются по расчетным значениям Rnm – например, согласно (12). Первый элемент матрицы (n = 1; m = 1) равен а 11 = ^11 ’ элементы первого столбца (n = 1; m [1; N]) вычисляются по формуле anm = Rnm /a11. Элементы главной диагонали (n = m) определя-

J n - 1

пт элементы, располо-к = I женные ниже главной диагонали (n > m; m > 1)

^Rnm      ' ^пк ^тк

– как                    Элементы располо- пт апп женные выше главной диагонали (n < m) являются нулевыми.

Для тестовой линейной N -элементной эквидистантной решетки с шагом d [6-12] коэффициент корреляции (12) при g = 2 равняется

^R_nm = expt-Cn-m)²^²//)^] ,       (13)

где D_R – радиус корреляции вдоль решетки для ошибки заданного вида.

После преобразования массивов независимых СЧ в коррелированные порядок дальнейших действий по реализации методики СИМ остается без изменений, поскольку на ход решения прямой внешней задачи СТА учет корреляционных связей формально не влияет. Процедура разыгрывания коррелированных ошибок с учетом (12)-(13) существенно усложняется – но если эти сложности преодолены, компьютеру остается только правильно подставлять в выражения для характеристики направленности (ХН) в нужном режиме [6-12] не одиночные значения СЧ, соответствующие ошибкам каждого заданного вида, а серии из N взаимно зависимых СЧ, соответствующих теперь и заданным значениям коэффициентов корреляции R_nm : для каждого n -го (каждого m -го) элемента СА свое собственное СЧ, зависящее от его номера.

Тестирование результатов СИМ не представляет труда: при R_nm → 0 в качестве частного варианта для ХН имеют место результаты, полученные при независимых ошибках [6-12]. В другом крайнем случае: когда R_nm → 1, аналогичным образом из общего решения следуют детерминированные (неискаженные ошибками) ХН СА.

Особенностью метода СИМ вообще является достаточно продолжительная и трудоемкая предварительная проработка всех обстоятельств предстоящего моделирования (описание предметной области СИМ и построение вербальных моделей;

определение исходных данных; выбор критериев для оценки прогнозируемых результатов и т.п.), связанная с обеспечением его требуемой точности и адекватности [19]. Сам процесс моделирования, напротив, существенно упрощается и ускоряется по сравнению с другими (аналитическими и численными) методами.

В заключение небольшое личное отступление. Представив к защите диссертацию в Аэрокосмический университет имени С.П. Королева, автор напористо уповал на казавшееся ему естественным обобщение с помощью финитных устойчивых моделей и широкого круга ПТ ТВ моделей и соотношений, полученных на основе нормального закона и центральной ПТ. Основанием для этого представлялась возможность варьировать при проведении компьютерных экспериментов параметр устойчивой модели γ вблизи значения γ = 2, присущего нормальному закону, чтобы пронаблюдать последствия этого на разработанных моделях реальных объектов.

После оживленной дискуссии некая неудовлетворенность теоретическими аргументами все же осталась. И вот, почти двадцать лет спустя, профессор В.В. Учайкин в разделе 3.4.5 с характерным названием: «Устойчивые распределения – экзотика или реальность?» работы [17] навел, по мнению автора, необходимый порядок в данном вопросе, подтвердив его предварительные (поверхностные и утилитарные) соображения. Вполне убедительным, в частности, теперь представляется вывод о том, что устойчивые законы играют (способны играть) роль эффективной промежуточной асимптотики при суммировании ограниченных случайных величин с ярко выраженными хвостами степенного типа – поскольку примерно о том же, с переменным успехом, пытался толковать на защите бывший диссертант...

Таким образом,если при моделировании СА предварительно исследовать их в полной мере не удается, целесообразно использовать возможности метода СИМ,связанные с применением ПТ ТВ.Поиск универсальной вероятностной модели, из которой можно получить все необходимые варианты типовых ПРВ,приводит к семейству одномерных устойчивых законов. Поэтому в рамках метода СИМ для моделирования ошибок была разработана процедура «разыгрывания» СЧ, подчиняющихся финитному устойчивому закону. Проблема выбора ИФР P(x) при этом существенно упрощается и удешевляется,– поскольку в рамках принятой универсаль- ной модели остается найти оценки числовых параметров (в статике или динамике), что намного проще,чем определять тип самого закона для ошибок каждого заданного вида.

О точности и адекватности метода СИМ

Дж. Форрестер [28] предложил для оценки адекватности СИМ представлять моделируемый объект (сложную систему) в виде «черного ящика» (см. рис. 1 ) – с возможностью затем модифицировать ее путем использования моделей состава и структуры объекта. Если на входе «черного ящика» присутствуют воздействия с параметрами,аналогичны-ми входным параметрам реальной системы, и на выходе имеют место характеристики с параметрами, в приемлемой степени совпадающие с выходными параметрами реальной системы, то такую СИМ-модель предлагается считать адекватной реальной системе. «Подгонять» модель под выходной результат можно путем варьирования («игры») параметрами – опыт показывает,что таким путем можно достичь приемлемой по Форрестеру степени адекватности модели, сократив число случайных воздействий на нее (в реальности число таких воздействий достигает 20-1 00) в десятки раз. Однако такая модель зачастую сама становится «игрушечной» и удовлетворительно копирует реальную систему (СА как объект СИМ) лишь в частных случаях, неадекватно реагируя на весь спектр возможных входных воздействий [20-21 ]. Как уже было сказано, избежать этого можно путем исследования конкретных СА [6]. Однако здесь также возникают сложности, связанные с проведением продолжительных и трудоемких исследований, не говоря уже о моделировании объектов с малой прецедентной базой.

В [18-19 и др.] показано, что задачи обеспечения адекватности и точности результатов СИМ, во-первых, достаточно сложны и неочевидны, а во-вторых, отличаются друг от друга по методам и средствами их решения применительно к СИМ-моделям разного типа. Вместе с тем они имеют и очевидные общие черты – причем определенные гарантии адекватности заложены в методику СИМ и напрямую зависят от эффективности реализации данного метода и правильной интерпретации полученных результатов.

Определение состава исходных данных

Статистическое исследование СА

Типы законов и оценки параметров

Поблочное моделирование СА

Рис. 4. Этапы СИМ, влияющие на адекватность модели СА

Первоначальные этапы СИМ, показанные на рис. 4, предусматривают определение состава исходных данных, влияющих на функционирование СА; проведение статистического исследования для сбора и обработки исходной информации о ней; идентификацию типов законов распределений исходных данных и расчет статистических оценок параметров этих законов; разработка математических моделей каждого блока СА и т.д. (более подробно см. в [19]).

Точность статистических оценок случайных параметров, влияющих на работу СИМ-модели, и степени ее адекватности реальной СА взаимосвязаны, поэтому путем изменения параметров точности, заложенных в СИМ-модель, ее адекватностью можно управлять. Основные факторы определяющие адекватность СИМ-модели СА: корректная методика разработки СИМ-модели; корректность реализации разработанной СИМ-модели; полнота и точность оценки случайных факторов, влияющих на моделирование СА и корректность методики тестирования модели также достаточно подробно рассмотрены в [19].

Напомним, что методика тестирования моделей реальных объектов часто базируется на правильном воспроизведении их характеристик в прошлом – с тем, чтобы сделать прогноз на будущее. Указать на объективные и универсальные способы проверки и доказательства адекватности результатов СИМ для объектов с малой прецедентной базой, кроме метода аналогии, нелегко. Поэтому многое здесь зависит от субъективных характеристик разработчика СИМ-модели СА: опыта, интуиции и т.п.

Для обеспечения требуемой точности результатов СИМ необходимо вычислять оценки полученных результатов по заданному числу реализаций СИМ-модели с помощью методов и средств математической статистики [19-20]. Поскольку при небольшом объеме выборки (числе реализаций до 100) точечная оценка может значительно отличаться от оцениваемого параметра (что при- водит к грубым ошибкам), здесь предпочтительны интервальные оценки [19].

Кратко остановимся на проблеме обеспечения кумулятивности исходных данных при проведении СИМ, под которой понимается свойство данных минимального объема адекватно отображать необходимые характеристики объекта [6]. Оценить кумулятивность можно на этапе тестирования СИМ-модели – «отсеивая», например, входные факторы A_n (см. рис. 1), мало влияющие на выходные результаты Y_z . Больше того: учитывая специфику СИМ можно существенно снизить требования к статистическим данным об ошибках в СА, упростив и ускорив процедуру ее предварительного исследования (см. этап 2 методики СИМ СА).

На рис. 5 в качестве иллюстрации (см. также рис. 2-3) показана финитная и симметричная ИФР ошибки P ( X ), X [– X_m ; X_m ]; которая, по определению, проходит через три фиксированные точки с координатами (– X_m ; 0); (0; 0,5) и ( X_m ; 1).

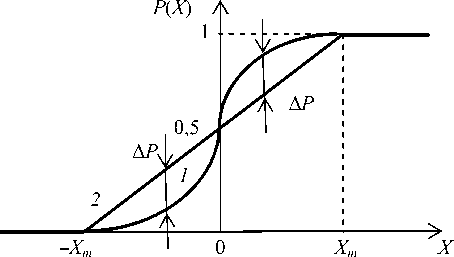
Рис. 5. Типовые ИФР ошибки с финитным и симметричным законом распределения P ( X ): 1 – предполагаемый реальный закон распределения ошибки X ; 2 – эталонный равномерный закон

Из рис. 5 следует, что оценить кумулятивность P(X) можно путем анализа влияния отличия ΔP предполагаемого реального закона 1 распределения ошибки от эталонной ИФР (например, с равномерным распределением в пределах –Xm; Xm) на результаты СИМ. Если выходные характеристики YZ при переходе от ИФР 2 к ИФР 1 меняются несущественно (с точки зрения эффективности функционирования СА), при проведении СИМ ошибки данного типа можно считать распределенными по эталонному (равномерному 2, нормальному и т.п.) закону. Если же изменение YZ окажется недопустимо большим (что также может иметь место на практике), от экспериментов с компьютерной моделью необходимо вернуться к исследованию реальных СА или физическому моделированию СА. В любом случае предполагаемый закон распределения ошибки 1 на рис. 5 имеет смысл воспроизводить с помощью достаточно общей, универсальной и управляемой вероятностной модели – примером чего является устойчивая модель (3)-(4).

В настоящее время наиболее распространены оценки точности и надежности СИМ, полученные в предположении подчинения их нормальному закону при выполнении условий центральной ПТ ТВ [20]. Но это не обязательно, поскольку класс распределений, к которым приводят ПТ ТВ, не ограничивается нормальным законом – в связи с чем в [31-32] аргументированы преимущества финитных устойчивых моделей по сравнению с моделями других типов. В частности, модель (3)-(4) обладает наилучшими возможностями для воспроизведения законов распределения ошибок в интересах СИМ СА: в том числе с так называемыми «тяжелыми хвостами», которые достаточно часто встречаются на практике.

По свойствам модель (3)-(4) близка к законам из семейства Стьюдента, которые широко используются в аналогичных целях [30]: с ростом числа реализаций N обе модели приближаются к нормальному закону (γ = 2); в другом предельном случае (γ = 1) – переходят в распределение Коши. Однако устойчивая модель остается справедливой как при малом объеме выборок: когда γ < 2, так и для больших выборок данных: когда с ростом N значение γ 2, и в целом воспроизводит максимально широкий круг возможных реальных ПРВ w ( X ). В то же время применение законов Стьюдента некорректно для распределений, отличных от нормального закона [31-32] – и эта некорректность сказывается при определении числа N реализаций имитационной модели в рамках СИМ.

Таким образом, применение устойчивых моделей в принципе способствует повышению точности и адекватности результатов СИМ. Однако реальные СА могут не соответствовать ни схеме обобщенного суммирования ни условиям применимости ПТ ТВ, причем наиболее трудным вариантом здесь представляется сочетание разного числа детерминированных и случайных аргументов (факторов), «включающихся» в процесс формирования ошибок в непредсказуемые моменты времени и в неизвестных заранее комбинациях. Тогда предсказывать закон распределения ошибок в виде (1) неправомерно и вся идеология вероятностного анализа нуждается в пересмотре.

Даже если в рамках моделирования по Форрестеру результат СИМ можно априори считать подчиняющимся устойчивому закону, необходимо учитывать его зависимость от модельного времени (см. далее), то есть рассматривать устойчивый случайный (аналогично нормальному) процесс. Адекватность устойчивого процесса с параметрами, зависящими от времени, результатам СИМ реальных СА нуждается в дополнительном исследовании – например, путем аппроксимации выходных гистограмм YZ с помощью (4). Такой подход можно считать перспективным при моделировании СА как объектов с малой прецедентной базой и в качестве первой стадии при исследовании объектов, к которым впоследствии можно будет вернуться для проведения СИМ по более строгой методике [20].

Вопрос о применении модели (3)-(4) для расчета числа реализаций N при проведении СИМ в условиях, когда оценки точности и надежности ненормализованы, может быть рассмотрен по аналогии с [32]. В частности, при произвольной форме ПРВ рассматриваемых случайных величин, аппроксимируемых в условиях применимости ПТ ТВ финитной устойчивой моделью, увеличение необходимого числа реализаций N не более чем в 1,37 раза по сравнению с нормальным законом гарантирует соответствие выборки экспериментальных данных требуемой точности ε и надежности р_д = 0,9 их оценки. В [32] подчеркнуто, во-первых, что этот результат получен вне зависимости от предположения о нормальности распределения рассматриваемой случайной величины и ее соответствии условиям применимости центральной ПТ ТВ, а во-вторых, что надобность в распределениях Стьюдента (базирующихся на нормальном законе, но дающих другой результат по сравнению с ним) при этом отпадает.

Отмечено также, что для малых объемов выборки использование законов Стьюдента приводит к затруднению ввиду того, что значения квантилей t_д для них и число реализаций N оказываются однозначно связанными друг с другом [30] вне зависимости от ε . В этом также проявляется противоречивость законов Стьюдента, которые, строго говоря, неприменимы для анализа и моделирования случайных величин с распределениями, отличными от нормального. Использование устойчивых законов в рассматриваемой ситуации снимает все противоречия [32].

Напоследок еще одна примечательная цитата. «Когда речь идет о любой реальной системе: технической, экономической, военной, – то процесс ее проектирования никогда не может быть четко сформулирован и сведен к решению какой-либо одной задачи или даже цепочки математических задач. Противоречивость требований к конструкции и наличие ряда других неопределенностей, с которыми неизбежно сталкивается человек, проектирующий систему, приводит к тому, что неформальный анализ, поиск компромисса занимает значительное место в процессе проектирования» [27]. Думается, что проблемы, связанные с оценкой адекватности и точности результатов СИМ (в том числе для решения внутренних задач СТА), заслуживают в настоящее время именно такого, неформального и креативного рассмотрения.

Динамическое моделирование СА

Имеет смысл обсудить здесь еще один, в достаточной мере парадоксальный и спорный момент. «Многие не признают потенциальной пользы модели, основываясь на том, что у нас нет достаточных данных для моделирования. Они уверены, что первым шагом должен быть широкий сбор статистических сведений. Верно же как раз обратное» [28].

В свое время автору пришлось затратить немало сил, столкнувшись с проблемой репрезентативности выборки статистических данных при проведении исследований в сфере электромагнитной безопасности [31]. Оказалось, что ни оппонентов, ни сторонников-коллег фактически нельзя ни в чем убедить: поскольку достоверных статистических данных об опасности неионизирующего электромагнитного излучения (ЭМИ) для биологических объектов на протяжении их жизни, по вполне понятным причинам, получить невозможно, а если ждать, пока они погибнут от разных причин, в том числе от ЭМИ – то некому будет подводить итоги такого «объективного» эксперимента. Понимали это, казалось бы, все – упорно повторявшие, тем не менее, что доказательств опасности ЭМИ современных радиосредств нет; наличие биоэнергоинформа-ционного излучения не доказано; любые представленные данные будут неубедительными, поскольку нерепрезентативны и т.п. В итоге, вместо принятия действенных мер, велась вялая полемика о том, какими методами и средствами лучше оценивать уровни ЭМИ; какими критериями при этом следует пользоваться; какие измерители и программные продукты надо разработать самим или купить за рубежом.

Чтобы подобные недоразумения не повторялись при исследовании СА, начинать надо именно с моделирования реальных антенн – располагая минимумом сведений для выдвижения гипотезы о структуре и принципе дейс- твия каждой такой системы. На данном этапе вербальное (от лат. verbalis – словесный) отображение (описание словами) СА представляет собой модель, на равных «конкурирующую» с математической моделью: достоинствами последней являются упорядоченность, стремление к устранению внутренних противоречий и точность, под которой понимаются конкретность, четкость, отсутствие неопределенности. Однако такая модель не обязательно более правильна в смысле соответствия реальной системе. Поскольку «мнение о том, что математическая модель не может быть построена, пока не будут полностью известны каждая константа и функциональная зависимость, является недоразумением» [28].

Учет динамики функционирования СА связан с усложнением процедуры СИМ [6-12], однако может оказаться необходимым для практики. В этой связи отметим, что рассмотренные в [6] примеры неуправляемых СА (ЭВМ с периферийным оборудованием; экранированная камера; АТС со жгутом проводов и др.) демонстрируют лишь малую часть наиболее очевидных и значимых в настоящее время приложений метода СИМ. Больше того: там же рассмотрен и другой, также достаточно важный для практики пример СА, каким является случайная активная фазированная антенная решетка (САФАР), которая вполне подходит под описание управляемой сложной системы как объекта СТА.

В теории управления главным признаком сложной системы считается иерархичность ее структуры, когда система состоит из подсистем и звеньев, которые сами являются системами. Сложную систему трудно оптимизировать, поскольку для нее не выполняется принцип максимума Понтрягина [18-20]: звенья стремятся оптимизировать собственные функционалы, при этом противоречат друг другу и не позволяют достичь оптимума в целом. Для неуправляемых СА при необходимости учесть изменения в режиме их работы можно использовать набор статических СИМ-моделей, соответствующих каждому фиксированному состоянию объекта. Для сложных управляемых СА типа САФАР в аналогичной ситуации требуется разработка динамических моделей (отметим, что САФАР в неуправляемом состоянии фактически неработоспособна). Управление САФАР очевидным образом предполагает применение динамических СИМ-моделей, если условия работы СА непрерывно изменяются (например, при мобильном базировании ее элементов).

Необходимость в динамическом моделировании СА может возникнуть и по другим причинам: например, когда нужно воспроизвести процесс функционирования ЭВМ; проанализировать эффективность защиты информации в сети многоканальных технических средств; отобразить работу комплексного (составного) канала утечки информации и т.п.

Если СИМ-модель призвана предсказывать поведение СА, она должна быть и достаточно точной (достоверной), и достаточно правильной (адекватной). Если же необходимо углубить знания об СА путем ее исследования, СИМ-модель может быть эффективной и в том случае, когда она правильно отражает лишь то, что мы считаем сущностью СА. В обоих случаях применение метода СИМ является обоснованным и оправданным – тем более что аналоги таких моделей (статических, динамических) известны [20].

Еще один существенный момент касается «строгости» математических методов, используемых при разработке СИМ-моделей. В [6] при описании предметной области для экранированной камеры с апертурами утечки использовались упрощенные электродинамические соотношения, что является допустимым и даже наиболее желательным при проведении СИМ. Одна из задач при построении СИМ-модели СА состоит в том, чтобы по возможности избегать продолжительных и трудоемких вычислений, негативно влияющих на ее простоту и наглядность. При этом качество и эффективность работы СИМ-модели определяются ее способностью воспроизводить (предсказывать) с требуемой точностью и надежностью лишь те характеристики реальной СА, которые необходимы для оценки их «вклада» (см. «Блок W» на рис. 1) в решаемую проблему. Поэтому СИМ-модель и должна в первую очередь выражать интересующую нас сущность СА – показывать, каким образом изменения режима функционирования или структуры приводят к изменению ее поведения и т.п. Когда набора статических СИМ-моделей для этого недостаточно, необходимо строить более сложную по структуре и трудную в реализации динамическую модель.

Если параметры и «правила работы» СА точно не определены, но являются управляемыми, с помощью метода СИМ можно исследовать варианты реализации СА из числа тех, которые могли бы существовать – несмотря на то, что речь в данном случае идет о правдоподобии, а не о точности и адекватности СИМ-моделей. Заметим, что это напрямую относится к целому ряду СА, представляющих практический интерес.

Испытание и тестирование СИМ-моделей СА ведет к двум проблемам: обоснованному выбору моделей тестовых сигналов и определению выходного критерия для оценки эффективности СИМ-модели. В [33-34] приведены экспериментальные данные, которые дают представление о многообразии сигналов, предназначенных для тестирования портативной ЭВМ с набором периферийных устройств. При этом тестовые сигналы должны соответствовать типовым режимам работы СА (гармонический, шумовой, импульсный и т.п. [6-12]).

Выходные критерии для оценки эффективности СИМ-моделей можно разделить на две группы: энергетические (от простого отношения «сигнал/ помеха» или «помеха/сигнал» до энергетического выигрыша в системе разнесенного приема или MIMO [35]) и оценивающие величину информационного ущерба за счет работы СА – вплоть до вычисления роста риска при принятии решений [36].

Важное значение при динамическом моделировании СА имеет проблема управления временем. Хотя в соотношения для анализа ХН входит только модельное время t [6; 8; 10], вопрос о его соотношении с реальным временем требует отдельного рассмотрения. Согласно [19-20], на первоначальном этапе СИМ необходимо выявить динамику СА в масштабе реального времени – понимая под этим, например, описание координат расположения каждого n -го элемента X_n ( t ); Y_n ( t ); Z_n ( t ) или в непрерывном аналитическом виде, или как последовательность фиксированных состояний (событий). Далее нужно задать параметры модельного времени (период и шаг моделирования). При этом под t понимается уже виртуальное время, в котором упорядочены события, сопровождающие работу СА, не обязательно строго пропорциональное реальному времени, а под периодом моделирования – промежуток t , соответствующий времени работы СА в СИМ-модели.

Известны два метода управления модельным временем. В рамках метода постоянного шага отсчет модельного времени ведется через фиксированные интервалы Δ t и события в СИМ-модели считаются наступившими (или не наступившими) по истечении каждого такого интервала. Данный метод применяется, если события появляются регулярно и достаточно равномерно по времени; невозможно заранее определить моменты появления событий; возможно аналитической описание Xn (t); Yn (t); Zn (t). Величина шага Δ t определяется средней интенсивностью событий или интервалом между наиболее значимыми (наиболее частыми) событиями на объекте СТА.

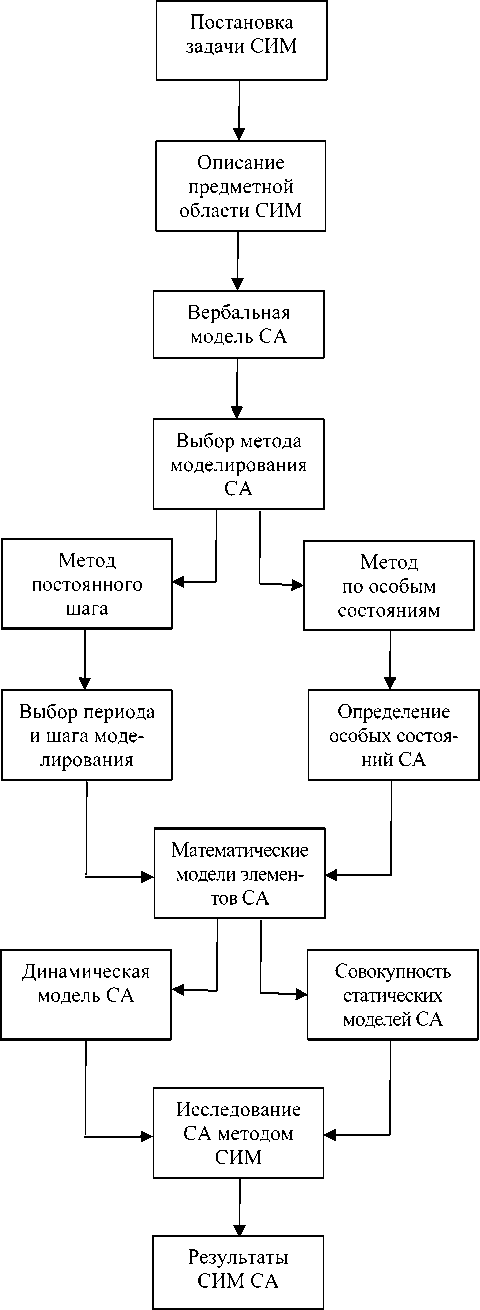
Рис. 6. Схема разработки и применения СИМ-модели СА

Метод по особым состояниям целесообразно использовать,если события распределяются неравномерно или интервалы между ними велики; важное значение имеет точность определения момента каждого события; в СИМ-модели можно реализовать последовательную обработку событий,в реальной СА происходящих одновременно.Представляется, что данный метод является своего рода «мостиком» при переходе от статических СИМ-моделей к динамическим: определив конечное число S особых состояний объекта,можно,как это уже было сказано, для каждого из них разработать статическую модель и исследовать динамику работы объекта СТА с помощью совокупности S таких моделей.

Схему разработки СИМ-модели для исследования СА иллюстрирует рис.6.Предполагается,что для СА в виде САФАР с мобильными элементами (в процессе ихнепрерывногодвижения)предпочтительнымможет быть метод постоянного шага,тогда какдля другихСА – метод моделирования по особым состояниям.На-помним,что в обоих случаях обязательным является по возможности более полный и точный анализ динамики работы СА в масштабе реального времени.

Заключение

В статье рассмотрен круг вопросов,связанных с применением метода СИМ для решениявнутренних задач СТА – моделирования законов распределения случайных факторов (ошибок), влияющих на работу СА различного назначения.Перспективными направлениями проведения дальнейших исследований являются:

• -    моделирование ошибок возбуждения на основе ПТ ТВ,приводящих к финитным устойчивым СИМ-моделям,с учетом специфики работы СА в гармоническом,шумовом,импульсном и радиоимпульсном режимах;

• -    решение прямых внутренних задач (с определением оценок числовых параметров и других исходных данных) для конкретных СА и рассмотрение возможностиадаптироватьметод СИМдлярешения обратных задач СТА;

• -    исследование СА методами и средствами системного анализа с целью анализа возможности сформировать базу данных по типовым параметрам сигналов СА, представляющих интерес для проведения СИМ и т.д.

В методическом плане наиболее важно,что проведение СИМ требует по возможности наиболее достоверного и адекватного описания СА,что создает трудности на первоначальном этапе, однако затем дает возможность использовать все преимущества метода СИМ и получить статистические данные (гистограммы ошибок, интерквантильные проме- жутки,средниезначения,дисперсииидр.),необхо-димыедлярешениязадачСТА.

Авторсчитаетсвоимприятнымдолгомпоздра-витьЯ.С.Шифринасзамечательнымюбилееми пожелатьздоровья,счастьяиудачивовсехделах. Уместнонапомнитьотом,что,во-первых,безпио-нерскихработ[1-3]никакихнынешнихдостижений СТАпростобынебыло.Во-вторых,чтоученикии последователиюбиляранаберегахВолгисегодня активнопродолжаютисследованиявобластиСТА.

ВсемыискреннеблагодарныВам,ЯковСоло-монович,запостоянноевниманиеидоброжелатель-нуюподдержку. ЕщеразсюбилейнымВасднем рождения!