Возможности индуктивного диэлектрического метода для изучения водных растворов

Существующие экспериментальные методы в какой-то мере себя исчерпали и не могут дать ответа на ряд вопросов об особенности воды не только в живых организмах, но и в ее обычном состоянии. В большинстве теоретических моделей воду рассматривают на основе различных модификаций двухструктурных моделей, предполагающих возможность нахождения воды в двух предельных состояниях, одно из которых всегда в той или иной степени льдоподобно. Но для доказательства возможности льдоподобного состояния в воде необходимо ее исследование на частотах порядка 10⁵ Гц, близких к 1/ т п льда, где т п — среднее время между перемещениями молекул Н₂О во льду.

Однако диапазон молекулярных процессов с характерными временами от 10–8 с до 10–4 с фактически является "белым пятном" в физике воды. Информацию о них можно получить лишь двумя методами: акустическим и диэлектрическим [1]. Интерпретация данных акустического метода неоднозначна, поэтому зафиксированное в ряде работ аномальное поглощение ультразвука на частотах ~105 Гц (смотри, например, [2]) в большинстве работ по воде игнорируется. Невозможна регистрация структурных эффектов в воде на таких частотах и общеизвестным диэлектрическим методом с использованием конденсаторных измерительных ячеек (С-ячеек) из-за больших потерь, обусловленных проводимостью.

В связи с вышесказанным особый интерес приобретает разрабатываемый в [3, 4] индуктивный диэлектрический метод (L-метод), позволяющий исследовать ориентационные процессы в ассоциированных жидкостях в диапазоне частот 10 кГц – 10 МГц, не искаженные токами проводимости. В L-методе исследуемая жидкость в диэлектрическом сосуде помещается в соленоидальные L-ячейки, подключаемые к колебательному контуру куметра. Этим методом величина тангенса угла диэлектрических потерь (tgS) жидкости и ее диэлектрическая проницаемость £ L (индекс L указы- вает на метод измерения) находятся в слабых вихревых электрических полях L-ячеек по соотношениям:

tg 5 =( Q i C 1 - Q 2 C 2 )/ Q 1 Q 2 ( C 1 - C 2 ), (1)

£ l = a (A C - A C *), (2)

где Q 1 , Q 2 , C 1 , C 2 — значения добротности и резонансной емкости колебательного контура до (индекс 1) и после (индекс 2) помещения сосуда с жидкостью внутрь L-ячейки; Δ C = C ₁ – C ₂ — изменение резонансной емкости при вводе в L-ячейку сосуда с жидкостью, а Δ C * — пустого сухого сосуда; α — постоянная измерительной ячейки, определяемая по калибровочным экспериментам [3, 4].

Рассмотрим, какую новую информацию о состоянии воды и водных растворов можно получить L-методом.

ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ

Особенностью определяемых L-методом диэлектрических свойств достаточно чистой воды с удельной электропроводностью χ = 1.5– 3 мкСм/см, получаемой с помощью бидистиллятора "Mera-Polna", является наличие в диапазоне частот 15 кГц-5 МГц сильной дисперсии £ _L (рис. 1). Отношение величины £ _L= £ max на частоте 15 кГц к £ _L = £ min на частоте 5 МГц воды близко к 3. В области дисперсии £ _L наблюдается максимум tg S , который в воде данным методом впервые был выявлен в [5, 6]. Поскольку значения £ _L и tg d находятся по изменению разных параметров колебательного контура, то наличие в одном и том же диапазоне частот дисперсии £ _L и низкочастотного максимума взаимно подтверждают их достоверность. Возможность артефактов исключается также отсутствием на данных частотах с 3 %-й экспериментальной погрешностью дисперсии £ L у других полярных жидкостей (например, у ацетонитрила, нитробензола, ацетона).

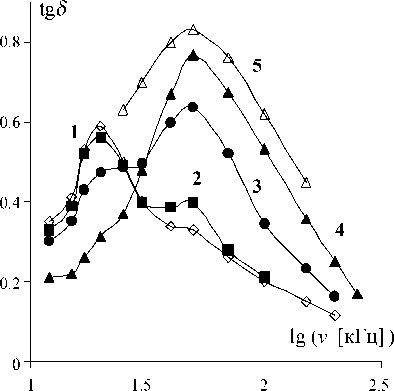
Рис. 2. Частотная зависимость tg δ воды с χ = 2.5 мкСм/см при температуре 0 ^оС ( 1 ), 20 ^оС ( 2 ), 30 ^оС ( 3 ), 50 ^оС ( 4 ), 70 ^оС ( 5 )

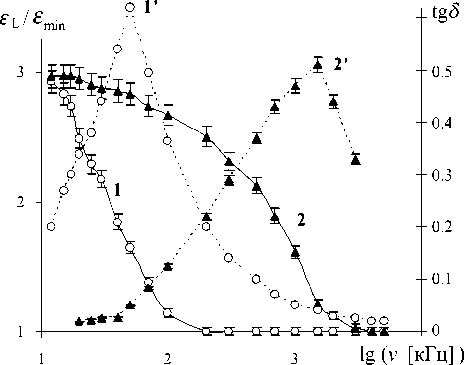
Рис. 1. Частотная зависимость ε L (кривые 1 , 2 ) и tg δ (кривые 1 ′ , 2 ′ ) для воды с χ =3 мкСм/см ( 1 , 1 ′ ) и водных растворов солей с χ =100 мкСм/см ( 2 , 2 ′ )

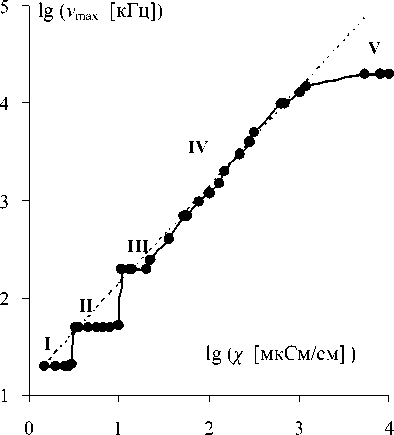
Рис. 3. Зависимость частоты ν от χ max

В водных растворах солей область дисперсии ε L и частота ν _max , на которой наблюдается максимум tg δ , смещаются в область более высоких частот без заметного изменения ε и ε    (рис. 1).

max min

Смещение области дисперсии εL при изменении состава или температуры воды с наибольшей точностью фиксируется по частоте νmax . Особый интерес представляет факт, что в воде с χ = 1.5– 2.5 мкСм/см при температурах 0–70 оС максимум водных растворов. Пунктир — расчет по уравнению (4)

tg δ может наблюдаться лишь на частоте ν _max (I) = = (20 ± 5) кГц или ν _max (II) = (50 ± 10) кГц. При повышении температуры величина tg δ на частоте ν _max (I) уменьшается, а на частоте ν _max (II), наоборот, повышается (рис. 2). Такое изменение частотной зависимости tg δ указывает, что с ростом температуры доля молекул воды, находящихся в состоянии, соответствующем ν _max (I) уменьшается, а ν _max (II), наоборот, увеличивается. Исчезновение экстремума на частоте ν _max (I) в чистой воде происходит при Т ∼ 40 ^оС, при которой в ней изменяется ход температурных зависимостей и других свойств (например, минимум теплоемкости и сжимаемости, изменение энергии активации всех явлений переноса) [1]. Таким образом, представленная на рис. 2 температурная трансформация частотной зависимости tg δ воды не противоречит известным данным о воде и отражает некие реальные изменения в ее состоянии.

В растворах с равной электропроводностью максимум tgδ наблюдается на одной и той же частоте. Справедливость данного вывода проверена на примере растворов NaCl, KCl, NaOH, KOH, HCl, KI, MgCl2, CoCl2, NH4SCN, CH3COONa. Поэтому представленная на рис. 3 зависимость νmax (χ) не зависит от химического состава водных растворов электролитов и является для них харак- теристической. На данной зависимости выделяются 5 характерных участков, которым предлагается поставить в соответствие 5 состояний воды.

Наибольший интерес представляют растворы электролитов малой концентрации с χ < < 20 мкСм/см, в которых при изменении температуры (рис. 2) и состава (рис. 3, 4) частота ν _max может иметь лишь 3 значения:

ν max (I) = (20 ± 5) кГц, ν max (II) = (50 ± 10) кГц, ν max (III) = (200 ± 20) кГц.

Этим частотам соответствуют три состояния воды: "вода-I", "вода-II", "вода-III". Поскольку на этих частотах при 0 ^оС наблюдаются максимумы tg δ не только воды с χ < 20 мкСм/см, но и льда из нее (рис. 4), то все эти состояния в той или иной степени "льдоподобны".

В состоянии "вода-I" может находиться лишь чистая вода с χ < 3 мкСм/см. Переход "воды-I" в "воду-II" можно осуществить повышением температуры (рис. 2) или концентрации солей (рис. 4). Согласно [7], подобие трансформации структуры воды при повышении ее температуры или содержания примесей по данным рентгеноструктурного анализа заключается в том, что оба эти фактора искажают тетраэдральную структуру воды. В таком случае переход "вода-I" → "вода-II" → "вода-III" сопровождается повышением степени искажения тетраэдральной структуры воды. Из того факта, что на частотах νmax (I); νmax(II); νmax (III) наблюдается максимум tgd не только у водных растворов, но и у льда из этих растворов (рис. 4), следует, что состояниям "вода-I", "вода-II" и "вода-III" свойственно преимущественно тетраэдральное льдоподобное расположение молекул Н2О.

В качестве следующего состояния "вода-IV" имеет смысл выделить состояние растворов с 20 >  χ < 1000 мкСм/см. В отличие от трех предыдущих состояний, частота ν _max таких растворов не постоянна. Она линейно растет при повышении χ (рис. 3), а ее зависимость от температуры описывается уравнением ν _max = ν ₀ exp( - W / RT ) при W = (2.4 ± 0.2) ккал/моль, близкой к энергии водородных связей в воде при Т > 50 ^оС [1]. Данный факт подтверждает, что растворы малой концентрации подобны чистой воде при повышенных температурах.

Растворы с 1 <  χ < 10 мСм/см находятся в состоянии "воды-V". В таких растворах максимум tg d

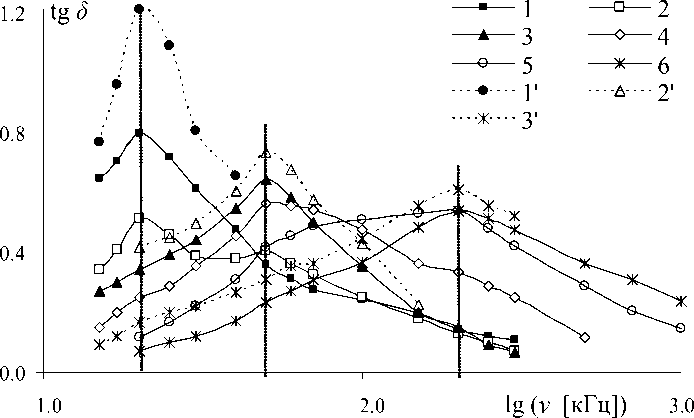
Рис. 4. Частотная зависимость tg δ при 20 ^оС воды и водных растворов NaCl с удельной электропроводностью: 1 — 1.5 мкСм/см; 2 — 2.5 мкСм/см; 3 — 3.6 мкСм/см; 4 — 6.5 мкСм/см; 5 — 13 мкСм/см; 6 — 22 мкСм/см; а также льда при 0 ^оС: 1 ′ — из воды 1; 2 ′ — из раствора 4; 3 ′ — из раствора 6

наблюдается на частоте ν _max (V) = 20–25 МГц независимо от состава раствора, его концентрации и температуры.

В заключение отметим, что введенная градация состояний относится к растворам с χ < 10 мСм/см, что для растворов сильных электролитов соответствует концентрациям менее 0.1 моль/л, которые в [8] предлагается относить к бесконечно разбавленным. То, что в растворах электролитов с такой концентрацией влияние индивидуальных свойств ионов пренебрежимо мало, в [8] установлено по диэлектрическим измерениям в СВЧ-области.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Для выяснения природы процессов, которые ответственны за возникновение в воде и ее растворах низкочастотной дисперсии ε _L и соответствующего ей максимума tg δ , очень важно сопоставление значений ε _L водных и неводных растворов солей. Как отмечалось выше, в обезвоженных чистых полярных жидкостях дисперсия ε _L отсутствует. Даже в спиртах отношение ε _max / ε _min на порядок меньше, чем в воде. Причем не исключено, что выявленная слабая 30 % дисперсия ε _L спиртов обусловлена примесью воды. Резкая дисперсия ε L в полярных жидкостях появляется при растворении в них солей (отношение ε _max / ε _min неводных растворов может достигать 9), причем предельно возможное повышение ε _max достигается при концентрациях ~10^–3–10^–2 моль/л.

В отличие от неводных растворов солей повышение концентрации солей в воде не увеличивает дисперсию ε _L в ней, а лишь смещает эту дисперсию в область более высоких частот. Следовательно, тот же самый фактор, который ответственен за появление низкочастотной дисперсии ε L в неводных растворах солей, действует даже в относительно чистой воде с χ = 1.5 мкСм/см. Достаточно очевидно, что этим фактором являются ионы Н⁺ и ОН^–, имеющиеся в любой воде, а также ионы примесей (электропроводности χ = = 1.5 мкСм/см эквивалентно наличие в воде ~10^–5 моль/л NaCl).

На особенность диэлектрических свойств растворов электролитов указывает работа Дебая [9]. В данной работе теоретически предсказано, что в растворах электролитов на частоте ν _i [Гц]= = 1/2 πτ _i , где τ _i — есть время восстановления атмосферы иона после его перемещения, должна наблюдаться низкочастотная дисперсия диэлектрической проницаемости. Полученное Дебаем выражение для ν _i можно представить в виде

ν _i = 1/2 πτ _i= χ / 2 πε ₀ ε , (4)

где ε — диэлектрическая проницаемость растворителя, ε 0 — электрическая постоянная. Оказалось, что если в (4) подставлять значения ε = ε _max , то рассчитанные значения ν _i очень близки к ν _max , а для водных растворов в состоянии "вода-IV" практически совпадают (рис. 3). Близость ν _i и ν _max установлена и на примере спиртовых растворов солей. Это исключает возможность чисто случайного совпадения и позволяет предполагать, что выявленные экстремумы tg δ обусловлены релаксацией ионных атмосфер.

Попробуем выяснить причины отклонений νmax от νi в "воде-I–III" и "воде-V". Для этого учтем, что за толщину ионной атмосферы ri в теории электролитов обычно принимается величина дебаевского радиуса экранирования. В случае водных растворов одно-одновалентных солей ri ≈0.3/ γ (нм), (5)

где γ — концентрация раствора в моль/л. Найденные на примере водных растворов NaCl значения γ [моль/л] и r _i [нм], соответствующие переходам растворов из одного состояния в другое, равны:

γ (I-II) ∼ 2 ⋅ 10^–5; γ (II-III) ∼ 7 ⋅ 10^–5;

γ (III-IV) ∼ 1.5 ⋅ 10^–4; γ (IV-V) ∼ 0.01;

r _i (I-II) ∼ 64 нм; r _i (II-III) ∼ 35 нм;

r _i (III-IV) ∼ 25 нм; r _i (IV-V) ∼ 3 нм.

Далее, рассчитав объем ионной атмосферы и поделив ее на объем одной молекулы воды, найдем число молекул N (I–III), входящих в ионную атмосферу в "воде-I–III": N (I) ∼ 10⁷; N (II) ∼ 2 ⋅ 10⁶; N (III) ∼ 5.5 ⋅ 10⁵. Маловероятно, что подобные ионные атмосферы могут существовать в виде одного гигантского кластера. Скорее всего они представляют собой совокупность более мелких относительно устойчивых фрагментов (будем называть их кластерами), внутри которых все молекулы воды связаны между собой водородными связями. При этом доля кластеров, содержащих хотя бы один ион примеси, в "воде-I–III" оказывается менее 1 % даже при условии, что кластеры состоят из 1000 молекул воды (при меньших размерах кластеров эта доля еще меньше). Поэтому процесс релаксации ионной атмосферы, а следовательно, и обусловленная этим процессом величина частоты ν _max в "воде-I–III" будет фактически определяться состоянием сетки водородных связей внутри кластеров из чистой воды.

Влияние центрального иона на процесс релаксации его ионной атмосферы в "воде-I–III" по предлагаемой модели будет в основном сводиться к искажению свойственной воде тетраэдральной льдоподобной структуры внутри кластеров из чистой воды из-за воздействия электростатического поля иона на ориентацию полярных молекул воды. Тогда немонотонное изменение νmax и наличие лишь трех его значений в воде с малым содержанием примесей, по-видимому, можно рассматривать как свидетельство того, что состояние сетки водородных связей в воде наиболее устойчиво при трех значениях углов связей, которым соответствуют три возможные тетраэдральные конфигурации во взаимном расположении молекул воды. В таком случае величина νmax — есть характеристика состояния сетки водородных связей внутри кластеров из молекул воды. Перспективность регистрации νmax как метода анализа состояний водных объектов подтверждается чувствительностью νmax к происходящим в воде структурным превращениям при изменении ее температуры (рис. 1), состава (рис. 2) и физических воздействий [5–6].

В водных растворах в состоянии "воды-IV" постепенно снижается число кластеров, не содержащих ионы примесей, в результате увеличивается искажающее влияние ионов примесей на взаимное расположение молекул внутри кластеров. При концентрациях, соответствующих переходу растворов из состояния "воды-IV" в "воду-V", радиус ионной атмосферы снижается до ~3 нм, что сравнимо с размером одного кластера, поэтому доля кластеров без ионов примесей стремится к нулю. В таком случае в "воде-V" повышение концентрации растворов сопровождается уже трансформацией кластеров в гидратные оболочки иона. Тем самым завершается преобразование структуры воды в структуру водных растворов.

В отличие от предложенной модели в [8] на основании диэлькометрических исследований в СВЧ-диапазоне полагается, что при γ < 0.3 моль/л в водных растворах солей одновременно присутствуют две структуры — слабо взаимодействующие между собой ионные атмосферы и водная матрица. По мере увеличения концентрации последняя постепенно вытесняется, структура раствора постепенно превращается в плотную упаковку из ионных атмосфер. При этом в [8] в растворах любой концентрации фактически полагается, что водная матрица неизменна, а под ионной атмосферой понимается лишь ближайшее окружение иона, т. е. его гидратная оболочка. Таким образом, по [8] изменение состояния разбавленных растворов при повышении их концентраций сводится к увеличению числа гидратных оболочек ионов и уменьшению доли неизменной водной матрицы по отношению к объему раствора.

Однако при справедливости данной модели в растворах с γ < 0.3 моль/л L-методом должны фиксироваться два экстремума tg δ : один, свойственный расположению молекул Н 2 О в чистой воде, другой — расположению этих молекул в гидратных оболочках ионов. Поскольку в растворах солей имеется лишь один экстремум tg δ , а свойственный чистой воде экстремум tg δ исчезает уже при γ > 2 ⋅ 10^–5 моль/л, то уже при таких концентрациях влияние ионов распространяется на всю водную матрицу, изменяя ее состояние. Поэтому ионная атмосфера не ограничивается гидратными оболочками.

Таким образом, исследования диэлектрических параметров водных растворов L-методом в диапазоне частот 10 кГц –50 МГц позволяют получить новые сведения о происходящих в них структурных трансформациях. С их помощью можно уточнить происходящие в растворах процессы, разработать более корректные их теории. Введенная градация состояний воды в ее растворах упрощает анализ свойств воды в различных объектах, а также позволяет систематизировать имеющиеся сведения о них.