Возможности использования фрагментов М-последовательностей с изменяющейся начальной фазой для корреляционных оптических рефлектометров

В современных оптических рефлектометрах в качестве зондирующего сигнала используется периодическая последовательность одиночных импульсов. Выведенная рефлектограмма представляет собой отклик волоконного тракта на одиночный импульс и сравнительно легко интерпретируется, позволяя получить информацию о распределении затухания и положении неоднородностей вдоль волоконно-оптического тракта. Для выделения сигнала обратного рассеяния из шумов фотоприемника необходимо увеличивать энергию зондирующего импульса за счет увеличения пиковой мощности и длительности импульса, а также проводить многократные измерения и усреднять значения сигнала обратного рассеяния в каждой точке волоконно-оптического тракта. Все перечисленные параметры, определяющие максимальный динамический диапазон рефлектометра, имеют ограничения. Пиковая мощность ограничена нелинейными явлениями в оптическом тракте, длительность импульса ограничена требованиями к разрешающей способности, а количество накоплений сигнала обратного рассеяния ‒ максимальным временем измерения.

Увеличение динамического диапазона при сохранении разрешающей способности возможно в корреляционных оптических рефлектометрах, в которых для зондирования волоконно-оптического тракта используются непрерывные псевдослучайные последовательности или их фрагменты. Зарегистрированный сигнал обратного рассеяния подвергается обработке, которая представляет собой вычисление взаимно корреляционной функции этого сигнала с порождающей его зондирующей последовательностью. Анализ показывает, что отношение сигнала обратного рассеяния к шуму и динамический диапазон возрастают пропорционально корню из числа элементов в фрагменте псевдослучайной последовательности по

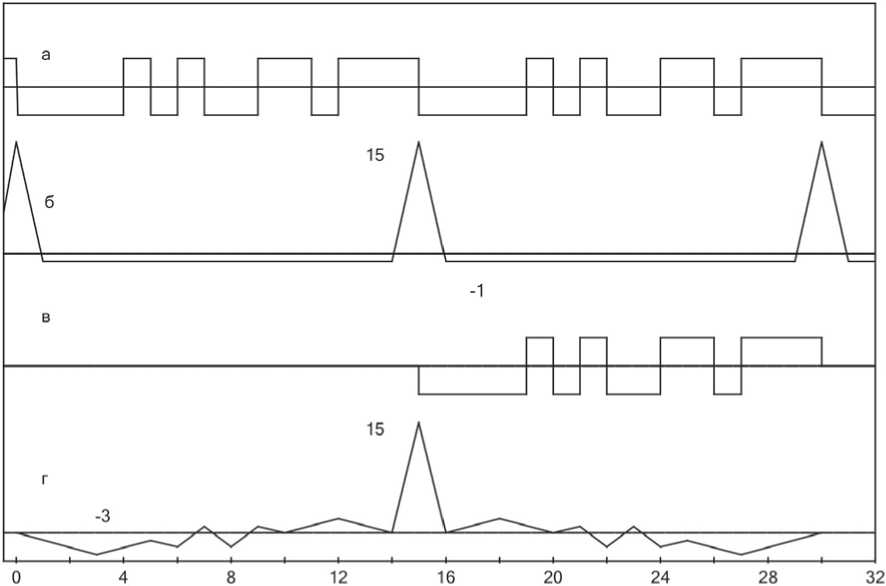
Рисунок 1. Автокорреляционные функции M - последовательностей

сравнению с рефлектометрами, использующими простой зондирующий сигнал.

Способы неискаженной регистрации рефлектограмм

Для неискаженной регистрации рефлекто-грамм корреляционным рефлектометром необходимо использовать зондирующие сигналы, представляющие собой пачку импульсов, с амплитудой, изменяющейся по закону кодовой последовательности, автокорреляционная функция которой имеет центральный лепесток максимальной амплитуды и минимальные боковые лепестки [1‒3]. Такими свойствами обладает непрерывная М-последовательность (рисунок 1, а , б ), но любой фрагмент этой последовательности имеет значительные боковые лепестки (рисунок 1, в , г ).

Представляется интересным создать такую комбинацию фрагментов этой последовательности, чтобы автокорреляционная функция этой комбинации имела центральный лепесток максимальной амплитуды и минимальные боковые лепестки. Такая комбинация может быть получена перебором фрагментов М-последовательности одинаковой длины с изменяющимися начальными фазами и дополнительным фрагментом, все значения элементов которого равны (+1).

Выражение для апериодической М-последо-вательности:

Am ={ a (k)}, k - 1,2,., M,

^EAM ^- “

где M = (2 ^y - 1) - число символов в М-после-довательности; у - любое целое число.

Фрагмент, вырезанный из этой М-последо-вательности։

• {a (k + m -1)}, (k + m -1)< M,

{a(k + m -1 - M)}, (k + m -1) > M, k - 1,2,., K, где (m -1) - фазовый сдвиг m-го фрагмента относительно первого зондирующего сигнала; Κ ‒ число импульсов в фрагменте.

Дополнительный фрагмент:

Eaо ={c(k)}, k - 1,2,.,K,

где c (k )- 1.

Автокорреляционная функция фрагмента М-по-следовательности։

^WAM ^{— {} w AM ⁽ u ^{) } —}

K

2 a (k + m -1) a (k + m -1 - u)

u-(1 - K),(2 - K).....(K - 2),(K -1).

Автокорреляционная функция дополнительного фрагмента:

21^ c ( k ) c ( k - u )

u-(1 - K),(2 - K),.,(K - 2),(K -1).

Сумма автокорреляционных функций։

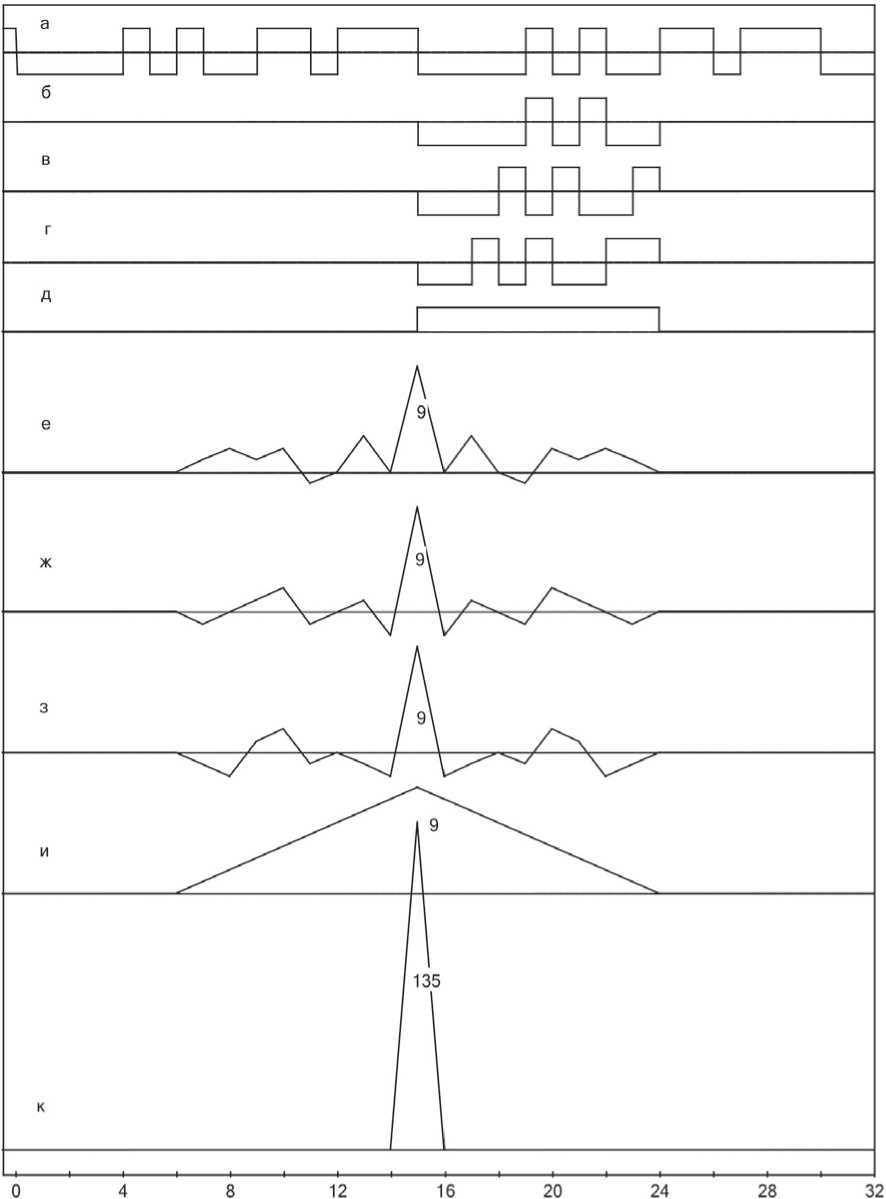
Рисунок 2. Автокорреляционные функции фрагментов М-последовательностей с изменяющейся начальной фазой

W y A = { W y A ( u )M £ W aM + W a 0

MK

= УУ a (k + m -1) a (k + m -1 - u) + m=1 k=1

K

+ У c (k)c (k — u) = k=1

к Г m

= У<У[ a (k + m -1) a (k + m -1 - u)] + k=1 L m=1

+ c (k) c (k - u)u = (1 - K),(2 - K),^,(K - 2),(K -1).

Из этого выражения видно, что если число и Ф 0, то символы a ( k + m - 1) и с ( k + m - 1 - и ) при изменении m от 1 до M образуют две сдвинутые на u друг относительно друга М-последовательности. Посимвольное перемножение двух М-последовательностей дает новую М-последовательность, сдвинутую относительно исходных. В полной М-последовательности символов со значением (+1) на один меньше, чем со значением (‒1). Так как последний член в рассматриваемом выражении всегда равен (+1), то при любом и Ф 0 выражение обращается в ноль.

Если и = 0, то сумма автокорреляционных функций:

WхA (0) = K(M +1).

На рисунке, 2, а изображена М-последо-вательность, на рисунке 2, б ‒ г ‒ первые три фрагмента этой М-последовательности, а на рисунке 2, д ‒ дополнительный фрагмент. Автокорреляционные функции этих фрагментов приведены на рисунке 2, е ‒ и , а на рисунке 2, к изображена суммарная автокорреляционные функция.

Видно, что эта функция идеальная, она имеет основной лепесток максимальной амплитуды и не имеет боковых лепестков. Если применяемая М-последовательность имеет значительное число элементов ( Κ ˃ 100), то вклад автокорреляционной функции каждого фрагмента в суммарную автокорреляционную функцию невелик.

Заключение

Использование М-последовательностей с изменяющимися начальными фазами позволяет формировать сложные зондирующие сигналы произвольной длительности, при этом их автокорреляционные функции остаются идеальными.

Работа выполнена при финансовой поддержке Фонда содействия инновациям в рамках договора № 3855ГС1/63276.