Возможности передачи и детектирования модулированных пучков с длиной волны 1530 нм в условиях случайных флуктуаций среды распространения

Одним из основных приложений световых пучков является беспроводная оптика ( Free-Space Optics , FSO), когда оптический канал проходит через случайную среду или вакуум. Практически неограниченный трафик сигнала на оптических частотах является выигрышной особенностью, которая отличает оптический канал от классической линии связи (радиоволны). С появлением высоконаправленного лазерного излучения дополнительное преимущество оптической коммуникации, связанное с безопасностью, стало очевидным [1–3].

Однако дальнейшему развитию этих систем связи мешает стохастичность среды, в которой передается сигнал. В атмосфере присутствуют как твердые, так и жидкие взвешенные частицы, движения потоков воздуха, тепловой градиент. Все это приводит к появлению эффектов естественных сред [4–9], таких как случайные мерцания ( scintillation ) и блуждания лучей ( beam wander ) у изначально детерминированных лазерных световых пучков. Именно влияние этих эффектов на технические характеристики оптических коммуникационных систем и ограничивает область их применения. Поэтому множество усилий направлено на поиск возможностей преодоления негативного влияния естественных случайных сред.

Модификация оптического канала связи возможна как путем использования средств формирования различных лазерных пучков со специальной пространственной и поляризационной структурой (вихревых, бездифракционных [10], мод высших порядков [11– 14] неоднородно поляризованных [15, 16]), так и путем совершенствования средств детектирования таких пучков [17–21].

Заметим, что особый интерес для уплотнения каналов передачи информации представляют пучки, несу- щие орбитальный угловой момент и имеющие бесконечное число возможных квантовых состояний [22]. Уже продемонстрированы значительные успехи в применении такого способа уплотнения каналов как в волоконных системах связи [23], так и в свободном пространстве [24, 25]. Обзор по исследованию и применению вихревых пучков в случайных средах можно найти в работах [26,27].

Устойчивость вихревых пучков к случайному воздействию отмечалась в нескольких экспериментальных работах [11, 17, 18, 28]. Заметим, однако, что оптические вихри высоких порядков менее устойчивы к возмущениям оптической среды. В работе [11] было показано, что вихревые пучки высокого порядка сохраняются в турбулентной среде на значительном расстоянии (несколько километров), но затем расщепляются на вихри первого порядка. В этой же работе утверждалось, что вихревой пучок может расщепляться, отклоняться, блуждать вне области детектора, но никогда не исчезает, т.е. сохраняется общий угловой момент поля. В работе [28] было показано, что пучки с более высоким оптическим вихрем больше подвержены влиянию случайных флуктуаций. Именно поэтому для экспериментов нами были выбраны вихревые пучки первого порядка.

В данной работе выполнено экспериментальное исследование распространения пучков, имеющих одинаковый вихревой топологический заряд, но различную пространственную структуру с длиной волны 1530 нм через случайную искажающую среду. Особое внимание уделено адаптации оптической системы детектирования вихревых пучков на основе корреляционной фильтрации к возникающим случайным угловым блужданиям пучков. Реализация экспериментов выполнялась с использованием ИК-лазера с волоконным выходом и бинарных амплитудных ДОЭ [29,30].

1.    Обоснование условий эксперимента и исследование воздействия аэрозольной преграды

Распространение структурированного лазерного пучка с вихрем через случайную среду моделировалось в работе [31] с помощью интегрального выражения, соответствующего расширенному принципу Гюйгенса–Френеля.

Было показано, что просто попадание пучка в случайную среду без всякого распространения уже приводит к искажениям, очень похожим на те, которые происходят и при дальнейшем распространении. Это служит обоснованием для применения при экспериментальном исследовании имитации протяженной случайной среды более короткими участками, чем могут быть при реальном распространении пучков в естественных случайных средах. При этом размерные параметры пучков надо выбирать такие же, как и для передачи на более дальние расстояния.

Выбор длины волны пучков для передачи информации обусловлен, прежде всего, удобством совместимости с существующими телекоммуникационными системами, в основном волоконными. В этом плане длина волны 1530 нм представляется достаточно удобной, поскольку близка к телекоммуникационной длине волны 1550 нм и представлена большим выбором достаточно дешевых лазерных диодов с различными способами вывода излучения. Исходя из этих предпосылок, в качестве источника излучения был выбран лазерный диодный модуль ЛПМ-1530 СТ мощностью 2 мВт и волоконным выходом. Как показывают расчеты, диаметр коллимированного пучка 25 мм является вполне достаточным для передачи на расстояния в сотни метров как с точки зрения расходимости, так и по отношению к характерным размерам тепловых потоков воздуха и других естественных преград. Поэтому для коллимации выходящего из световода излучения мы использовали коллиматор F810FC-1550. Данный коллиматор совмещается с оптикомеханическими компонентами Thorlabs, рассчитанными на дюймовую оптику, при помощи адаптера для цилиндрических компонентов AD15F с резьбой SM1. Для наблюдения за пучками мы использовали ПЗС-видеокамеру VS320-BCL производства КБ Вита, позволяющую производить съемку изображений с частотой 50 Гц. В диапазоне длин волн 900–1700 нм данная камера имеет очень большой запас чувствительности при 2 мВт мощности лазера. В условиях эксперимента для согласования меняющейся в широких пределах интенсивности пучка с динамическим диапазоном камеры, для ослабления пучка удобнее всего использовать поляризатор LPMIR050-MP2, имеющий поляризационный контраст не хуже 1:2000 в диапазоне длин волн 1500–5000 нм. Кстати, измерения показали, что в условиях свободной укладки подводящего излучение световода поляризация лазерного излучения на выходе световода очень близка к линейной.

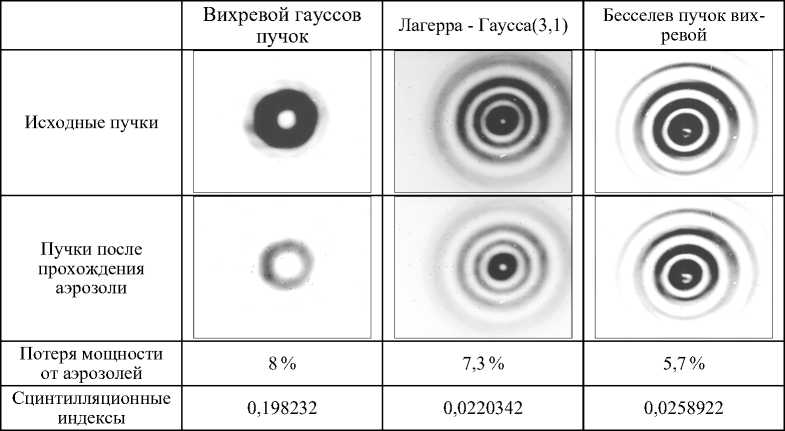
В условиях большого запаса мощности лазера было решено использовать для формирования пучков имевшиеся в наличии бинарные амплитудные ДОЭ [29], хорошо подходящие по размеру под дюймовую оптику. Данные ДОЭ представляют собой кодированные ДОЭ для работы в первом порядке дифракции, изготовленные в виде хромовой маски с толщиной хрома не менее 50 нм. Такая толщина хрома, как следует из справочных материалов, обеспечивает пропускание не более 6% интенсивности излучения на длине волны 1530 нм. Имелось три таких ДОЭ, все они формируют вихревые пучки первого порядка в плюс-минус первом порядке дифракции. Отличия между этими ДОЭ заключаются в амплитудно-фазовых распределениях сформированных пучков, которые соответствуют: моде вихревого Гауссова пучка, аппроксимации моды Лагерра–Гаусса (3,1) и усеченному до трех колец вихревому пучку Бесселя. Соответственно, все три пучка в какой-то степени обладают свойством самовоспроизведения и могут использоваться для атмосферной связи. В первой строке табл. 1 приведены зарегистрированные распределения интенсивности указанных пучков на расстоянии 2 м от коллиматора.

Следующим этапом эксперимента было исследование влияния аэрозолей на распространение пучков. Общая схема экспериментальной установки приведена на рис. 1. Установка содержит формирователь вихревых пучков (ДОЭ), имитатор случайной среды – нагреватель, анализирующий модан (Модан), Фурье-преобразующую линзу (Л2) и ПЗС-матрицу. Для создания искажающей среды в этом случае вместо нагревателя использовалась установка генерации аэрозолей DF-400W, которая заполняла аэрозольным облаком через трубопровод специальный контейнер около 1 м в длину вдоль оптического пути. Для входа и выхода излучения в контейнере имелись открытые окна. Контейнер способствует воспроизводимости условий эксперимента, так как в нем через достаточно короткое время устанавливается некоторая равновесная концентрация аэрозольных частиц. Такие условия эксперимента приближены к условиям эксперимента в работе [20], только в воздушной среде.

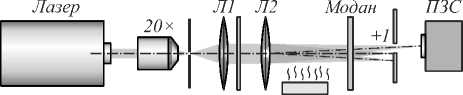
ДОЭ Нагреватель

Рис. 1. Схема экспериментальной установки

Во второй строке табл. 1 приведены зарегистрированные распределения интенсивности указанных пучков, прошедших через аэрозольное облако в контейнере в отсутствие модана перед регистрирующей камерой. Что касается интегральных характеристик прошедшего через аэрозоль излучения, то наиболее важной является потеря мощности, и она составила для всех трех пучков примерно одинаковую величину около 6,5 % (см. табл. 1). Измерения проводились измерителем мощности Thorlabs – PM122D с германиевым детектером. Другой важной характеристикой является сцинтилляционный индекс η [32]:

σ с ² = ( I ²/ I )²) - 1,                                    (1)

где I – среднее значение интенсивности пикселей одного кадра фото приёмного устройства; ( I ) - среднее значение интенсивности всех кадров.

Значения индекса сцинтилляции для исследуемых мод приведены в третьей строке табл. 1.

Как видно, он примерно одинаков у двух многокольцевых пучков и меньше, чем у Гауссова пучка. Это можно объяснить большей площадью сечения, по которой происходит усреднение и, как следствие, усреднением по большему ансамблю.

Табл. 1. Распространение различных пучков в случайной среде на расстояние 1000 мм (негативные изображения)

• 2.    Исследование воздействия тепловых потоков и влияния блужданий пучков на работу корреляционной системы распознавания

В работе [21] было предложено использовать оптический коррелятор для распознавания вихревых пучков, прошедших через случайную среду. При этом важнейшей характеристикой такого коррелятора является его устойчивость к сдвигу распознаваемых пучков с вихрями во входной плоскости. В работе было показано, что в случае параллельного сдвига пучков во входной плоскости соответствующие им корреляционные пики не пропадают, а лишь претерпевают аналогичный масштабный сдвиг в соответствующих областях выходной плоскости. Как известно [33], наличие турбулентности в атмосфере приводит к случайным угловым смещениям энергетического центра тяжести распространяющегося оптического пучка. Угловое смещение пучка приведет к сдвигу центра пучка в спектральной плоскости и соответствующему ослаблению корреляционных пиков в зависимости от величины сдвига.

Компенсация угловых смещений пучка является достаточно сложной задачей, и для ее решения разработаны специальные системы [32]. Однако, если угловые смещения не очень велики, их влияние на ослабление корреляционных пиков также может оказаться небольшим. Проводить какие-то предварительные расчеты, видимо, нецелесообразно, поскольку готовых данных о блужданиях пучков в конкретных условиях наших экспериментов нет. Учитывая это обстоятельство все исследования как параметров блужданий, так и образования корреляционных пиков проводились в рамках одного эксперимента.

Очевидно, что в условиях угловых смещений пучков наличие первого Фурье-каскада коррелятора необязательно. Смещение центра пучка в плоскости корреляционного фильтра будет наблюдаться и в том, и в другом случае, причем примерно в равной степени, поскольку для условий оптической связи удовлетворяется условие дальней зоны. Разумеется, такой подход возможен только для оптических пучков с поперечным распределением комплексной амплитуды, инвариантным к преобразованию Фурье. Обоснованием такого подхода является то, что для оптической связи наилучшими как раз и являются такие пучки, распределение комплексной амплитуды которых в дальней зоне дифракции с точностью до масштаба повторяет исходное распределение в сформированном пучке, то есть пучки, обладающие свойствами самовоспроизведения. В частности, таким свойством обладают вихревые модовые пучки, применение которых рассматривается в данной статье.

Сам эксперимент проводился с тем же набором оборудования, что и в предыдущем эксперименте, только на место контейнера с аэрозолью устанавливался спиральный нагреватель прямоугольной формы со сторонами 15×20 см и мощностью 600 Вт, на котором поддерживалась температура 530 – 580° С. Свет распространялся над нагревателем на расстоянии 15 см по направлению длинной стороны. Легко понять, что угловые смещения пучков, полученные на сравнительно небольшом отрезке оптического пути, по своему воздействию на процесс фильтрации будут аналогичны полученным на более длинных участках турбулентности. Единственное отличие состоит в том, что при увеличении длины распространения ли- нейное смещение пучка может приводить к его выходу из апертуры оптической системы, но мы не будем рассматривать такие случаи. В табл. 2 приведены данные по смещению энергетического центра тяжести разных пучков при их распространении после участка с потоком нагретого воздуха на расстояние около метра. Видимых искажений распределения интенсивности пучков при этом не происходит.

Таким образом, для определения устойчивости вихревых пучков к искажениям в турбулентной атмосфере достаточно оценить величину смещения положений центров тяжести изображений, определяемых в долях пикселя по зависимостям [34]:

X =

NM

ZZ I nm n n = 1 m = 1

NM

ZZ I n

NM

ZZ I n , m m n = 1 m = 1

NM

ZZ I n , m

где I n , m – интенсивность пикселя n, m (порядковые номера пикселей по столбцам и строкам матрицы фо-топриёмного устройства); N, M – число столбцов и строк матрицы фотоприёмного устройства.

Табл. 2. Смещения энергетического центра тяжести (негативные изображения)

Вихревой гауссов Лагерра–Гаусса пучок (3,1)

Бесселев пучок вихревой

Среднее и максимальное отклонения центра тяжести, пикс

0,7227 / 5,2528 0,837467 / 5,2766 0,7017 / 3,7034

Нагреватель располагался в начале оптического пути, непосредственно за формирующим ДОЭ. Из данных табл. 2 можно получить соответствующие углы, в пределах которых происходят смещения пучков. Легко видеть, что эти углы не превышают 10–4 рад. Аналогичный эксперимент проводился и для случая формирования изображений пучков в плоскости ПЗС-матрицы при помощи телеобъектива Юпитер-37А. Общее расстояние между оптически сопряженными плоскостями за нагревателем и плоскостью ПЗС составляло около 670 мм, причем на ПЗС получалось уменьшенное изображение. Кратность уменьшения при этом около 1:2,5. Средние флуктуации центра изображения при этом снизились приблизительно в 2,5 раза и составили 0,2844 пикселей на матричном сенсоре. Это лишний раз показывает правильность отказа от одного линзового каскада в оптической схеме.

Поскольку для формирования вихревых пучков в эксперименте использовались соответствующие ДОЭ с несущей частотой [30], работающие в первом порядке дифракции, часть оптической установки за формирующим ДОЭ была установлена под углом к оптической оси и настроена на прием первого порядка дифракции.

В качестве анализирующего модана использовался многоканальный фазовый фильтр, согласованный с угловыми гармониками первых трех порядков [35– 37]. В эксперименте использовалась Фурье-преобразующая линза с фокусом 500 мм при диаметре освещающего пучка 15 мм. Изображение в выходной плоскости коррелятора, полученное в отсутствие тепловых потоков, приведено на рис. 2. Хорошо виден корреляционный максимум в центре порядка дифракции, соответствующего вихрю 1-го порядка. Далее включался нагреватель и были получены изображения в корреляционной плоскости при наличии турбулентности. Пример таких изображений в разные моменты времени приведен на рис. 3. На этих изображениях так же, как и у исходного пучка, во времени происходят случайные смещения энергетического центра тяжести, но существенных изменений интенсивности корреляционного пика не происходит. Бо- лее точно можно проанализировать этот процесс, ес- ли по аналогии с исследованиями прохождения пучка через аэрозоли применить понятие сцинтилляционного индекса к интенсивности корреляционного пика. В нашем случае значение индекса п составило 0,00057, что существенно меньше, чем в случае аэрозольной преграды. Таким образом, можно сделать вывод, что предложенная модификация корреляционного метода распознавания вихрей может успешно применяться в условиях турбулентности, сходных с условиями по- становки эксперимента.

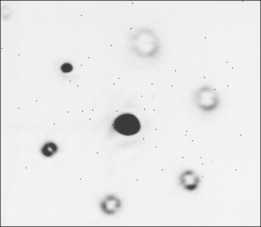
в отсутствие тепловых потоков (негативное изображение)

Рис. 2. Изображение в выходной плоскости коррелятора

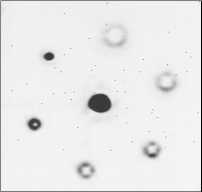
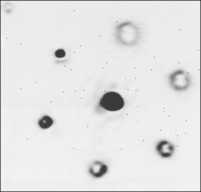
Рис. 3. Примеры распределения интенсивности в выходной

плоскости коррелятора при наличии тепловых потоков (а, б – в разные моменты времени) (негативные изображения)

Заключение

Теоретически и экспериментально исследовано распространение различным образом структурированных вихревых пучков с длиной волны 1530 нм через случайную искажающую среду. Показано, что зату- хание пучка не превышает 8 % при максимально достижимой концентрации аэрозольных частиц на длине распространения около 1 м. По сцинтилляционным индексам наилучшие результаты получены для многокольцевых пучков. Эксперименты также показали применимость модифицированного оптического коррелятора для детектирования наличия вихревой фазы в условиях угловых блужданий пучков, вызванных потоком теплого воздуха.

Работа выполнена при поддержке Министерства науки и высшего образования РФ (МК-1797.2019.2) в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в части расчета ДОЭ, гранта РФФИ (№18-29-20045 мк) в части экспериментальных исследований, а также гранта РФФИ (№18-07-01470) в части формирования вихревых пучков.